一类非线性奇异分数阶微分方程解的存在唯一性
姜聪颖,侯成敏
(延边大学 理学院, 吉林 延吉 133002 )
首先利用Banach不动点定理和Schauder不动点定理得到了此类非线性分数阶微分方程解的存在性和唯一性的相关结论和定理,然后利用两个实例验证了文中所得的主要结论.
0 引言
近年来许多学者研究了非线性奇异分数阶微分方程,并得到了许多较好的研究结果.例如:在文献[1]中,Agarwal等研究了奇异分数阶边值问题解的存在性:
其中: 1<α<2, 实数μ满足0<μ≤α-1,Dα为标准 Riemman -Liouville 分数阶导数,f满足[0,1]×(0,∞)×R上的Caratheodory条件,f(t,x,y)在x=0处奇异.
在文献[2]中, Yan等研究了一类积分边界条件下分数阶微分方程解的存在唯一性:
在文献[3]中, Guezane -Lakoud等讨论了带有分数阶导数条件的边值问题解的存在性和唯一性:

基于上述文献研究,本文研究一类非线性奇异分数阶微分方程解的存在唯一性:
(1)
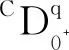
1 预备知识及其原理
定义1[4]令α>0,n=[α]+1.如果g∈ACn([a,b]), 则Caputo分数阶导数的定义为
在[a,b]上几乎处处存在([α]表示实数α的整数部分).
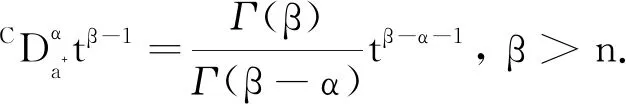
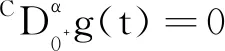
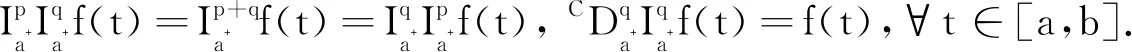

引理5(Schauder不动点定理) 令(E,d)是一个完备空间,U为一个E的闭凸子集,并且令A∶U→U是一组使{Au:u∈U}在E中是相对紧的映射,则A至少有一个不动点.
引理6对于y∈C[0,1],n-1
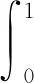
(2)
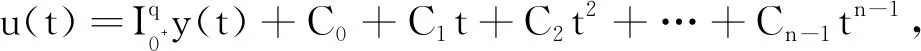
因此,u(t)可以写为
其中G(t,s)为式(2)中所定义的.证毕.
2 主要结果及其证明



当t0∈(0,1),∀t∈(t0,1]时,有
当t0∈(0,1),t∈(0,t0]时, 其证明过程与t0∈(0,1)和∀t∈(t0,1]的情况类似,故略.
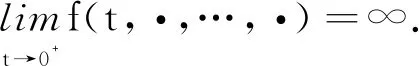


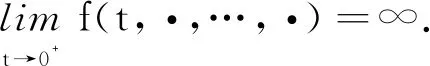
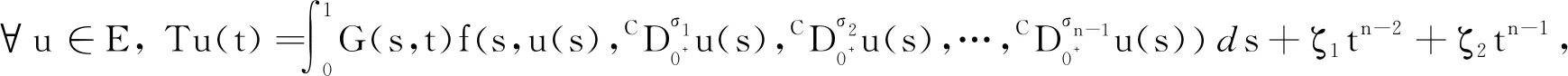
(3)
另外,由定理1还可得
(4)
|ζ2tn -1|≤LB0+|ζ1|+|ζ2|;
下面证明T(Ω)是等度连续的.对于所有的t1,t2∈[0,1],t1 (5) (6) 综合定理1、定理2和定理3,再由Arzela -Ascoli理论可得T是完全连续的. 定理4假设(H1)和(H2)成立,那么边值问题(1)有唯一解. (H2)θ=max{nlB0,nlB1,…,nlBi,…,nlBn -1}<1,i=1,2,…,n-1. 证明首先证明T是一个压缩算子.令u,v∈E, 则由(H1)以及式(3)和式(4)可得 (7) (8) 例1考虑如下分数阶边值问题: (9) 例2考虑如下分数阶边值问题: (10)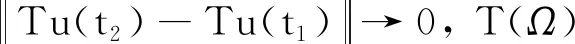
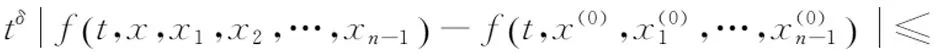


3 例子

