自重固结下的吹填场地桩基负摩阻力解析解

杨怡青， 李传勋

(江苏大学 土木工程与力学学院， 江苏 镇江 212013)

随着经济的高速发展，城市用地愈发紧张，尤其是在沿海城市这一问题更为突出.在此背景下，大量难以处置的疏浚淤泥被用作填海造陆的主要原材料.但与砂石相比，疏浚淤泥作为吹填材料具有压缩性大、渗透性低等特点，往往处于欠固结状态，故吹填场地中桩基础易出现负摩阻力的现象.例如，天津某吹填泥浆场地也证明吹填土的固结沉降会对桩基础产生向下的负摩阻力[1].若负摩阻力设计计算不当，将会对桩基承载力及其变形产生重要影响.因此，研究吹填场地中桩基础的负摩阻力问题具有重要的理论和实际意义.

早在20世纪50年代就有人提出了桩基负摩阻力概念，并通过大量现场测试，探讨了中性点分布的大致位置及负摩阻力的初步估算方法.在太沙基固结理论的基础上，求得了单桩负摩阻力随时间的变化规律.虽然以上经验方法计算简便，但是未能考虑桩侧土沉降对负摩阻力影响的时间效应及空间效应，同时桩土相互作用均采用线弹性模型，而实际上并非服从线弹性模型.基于此，国内外学者多采用荷载传递分析法分析桩基受力特性.文献[2]采用双曲线函数，得到了成层地基中桩基负摩阻力的数值解.文献[3]基于前人试验成果，对双曲线函数进行改进，得到负摩阻力的数值解.文献[4-5]建立了指数型荷载传递函数，分析了负摩阻力对桩基承载特性的影响.文献[6]引用库伦摩擦模型，以双折线函数建立数值计算模型.文献[7-8]采用双折线函数，得到桩基摩阻力随深度变化的解析解.文献[9]在太沙基一维固结理论的基础上引入改进的佐藤悟双折线模型，求得了某时刻桩身摩阻力随深度变化的分布规律及中性点位置.

目前学者主要采用双曲线函数及双折线函数模拟桩土间的荷载传递关系.但采用双曲线函数时，仅能获得其数值解，且求解过程相对复杂.采用双折线函数时，一些学者则假设桩周土沉降与深度呈线性相关.而对于吹填土这种具有不良特性的地基土相关研究更是鲜见报道.

为此，笔者将吹填土及其下卧层视为双层地基，采用双折线函数，研究其在吹填土自重荷载下的固结问题，获得桩侧摩阻力随深度和时间变化的解析解.并基于该解析解，分析各影响因素对桩基中性点位置、桩侧摩阻力及桩身轴力等的影响.

1 桩周土固结及桩土作用模型

1.1 问题描述

均质地基土层上开展吹填工程，将原土层与新近吹填土层视为双层地基，如图1所示.图1中，双层地基中上层土为吹填土，γ′为有效重度，H为桩长，h1和h2分别为上、下土层的厚度.σ(x)为土体有效应力，其中σ1和σ2分别为深度h1和h2处土体有效应力.固结时间因子Tv1=cv1t/H2为打桩时的时间因子，cv1为上土层的固结系数.

图1 分析模型

1.2 桩周土固结模型

吹填土的有效重度为

γ′=(Gs-1)γw/(1+e0)，

(1)

式中：Gs为颗粒比重；γw为水的重度；e0为吹填土颗粒沉积下降稳定后的初始孔隙比.

吹填土自重应力在h1范围内沿深度线性增加，双层地基内应力分布见图1.鉴于场地平面尺寸远大于主要受力层厚度，故将吹填土及其下卧土层在吹填土自重下的固结问题视为一维问题.除地基内附加应力分布如图1所示外，作出与太沙基一维固结理论相同的假定，根据文献[10]给出的双层地基固结解，得到t时刻第i层土深度x处桩侧土的沉降变形vix为

(2)

(3)

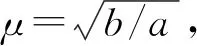
1.3 桩土相互作用模型

桩土间正负摩阻力均服从相同的荷载传递模型，认为桩侧摩阻力和端阻力与桩土相对位移呈正比.当相对位移达到一定值后，考虑桩周土体固结效应所引起的比例系数变化，采用如图2所示的桩土荷载传递模型中的双折线函数.图中fx为单位厚度土体所受摩阻力，kN·mm-1；R为桩端土反力，kN；fu和Rb分别为弹性阶段桩侧摩阻力极限值和桩端土反力极限值，kN；zx为深度x处桩土相对位移，zui和zb分别为桩周土和桩端土的弹性变形极限值，mm；k1和k2为桩周吹填土的刚度系数，kN·mm-2；k3和k4为原位土体的刚度系数，kN·mm-2；k5和k6均为桩端土体反力系数，kN·mm-1.

图2 桩土荷载传递模型

2 荷载传递模型

2.1 基本微分方程

任意深度x处取一桩体微元分析，由桩土平衡条件及桩体本构方程得

(4)

式中：A为桩身截面积；E为桩身弹性模量；uix为在第i层土深度x处的桩身压缩量.第i层土内桩土相对位移zix为

zix=uix-vix.

(5)

联立式(4)与(5)，得到了描述桩土作用的微分方程：

(6)

2.2 桩侧荷载传递

随着桩周土的固结，桩周土强度逐渐增大，桩周土与桩的界面传递函数从上至下渐渐由双折线模型中第1阶段过渡到第2阶段，同时桩端土也会出现同样现象.因此分3种工况进行讨论、求解.

1) 工况1：桩周与桩端土界面传递函数均处于第1阶段.此情况下桩侧摩阻力的模型为

(7)

将式(2)、(3)和(7)代入(6)，得到控制方程：

(8)

(9)

边界条件和层间连续性条件为

(10)

(11)

u1|x=h1=u2|x=h1，

(12)

(13)

式中：p为桩顶荷载.

微分方程(8)和(9)的通解为

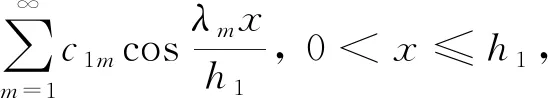
(14)

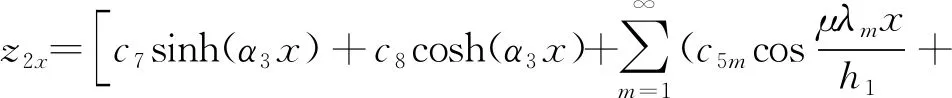
(15)

依据求解条件可得通解中的系数c及桩身轴力、中性点位置和下拉荷载，感兴趣者可自行推导，以下几种工况同样不再进行详细推导、赘述.

2)工况2：部分桩周土界面的传递函数进入第2阶段，而桩端土仍处于第1阶段.当桩土相对位移较大时，桩周土由浅至深逐渐进入硬化状态，如图3所示.

图3 桩周土进入硬化阶段

由于吹填土层沉降大，认为临界点深度h位于下卧层内.桩侧摩阻力为

(16)

将方程(16)代入方程(6),得到控制方程：

(17)

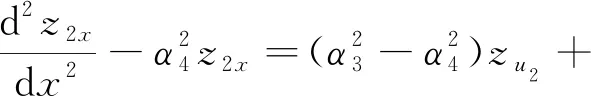
(18)

(19)

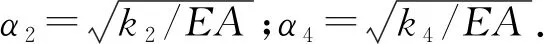
(20)

(21)

u1|x=h1=u2|x=h1，

(22)

u2|x=h-=u2|x=h+，

(23)

(24)

(25)

微分方程(17)、(18)和(19)的通解为

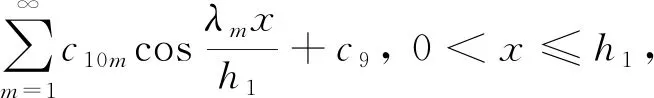
(26)

(27)

(28)

3) 工况3：桩周土与桩端土均进入第2阶段.此时桩侧摩阻力为

(29)

将方程(29)代入方程(6)，得到控制方程为

(30)

(31)

(32)

(33)

u1|x=h1=u2|x=h1，

(34)

(35)

求解微分方程(30)和(31)，得其通解为

(36)

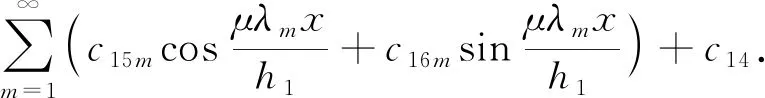
(37)

3 工程案例对比分析

3.1 桩周土体和桩体参数

上层吹填土厚度h1=4.4 m.原状土视作均匀土层，厚度h2=30.6 m.参照文献[11]，桩周土体参数取值如表1所示.

表1 桩周土体参数

调研案例中所涉及的各土质特性参数，结合既有文献报道的双折线模型的参数变化范围[12-13]，上、下土层双折线模型参数取值如下：k1、k2、k3和k4分别为3.54×10-3、1.35×10-3、2.971×10-2和9.55×10-3kN·mm-2，k5和k6分别为9.3×10-4和8.4×10-4kN·mm-1.桩体参数如下：E=3.6×104MPa，桩径D=1.00 m，周长U=3.14 m，H=35.00 m.

3.2 对比验证

根据实测资料文献[11]可知：2#试桩桩侧吹填土层和原状土层的极限摩阻力分别为15.00和36.68 kPa，桩端土极限摩阻力为80.00 kPa，由此判断桩端土与桩周土均处于弹性阶段.应用工况1计算结果与实测数据对比，当桩周土体固结度Ust=90%,时间因子Tv1≈1时，打设桩基.在固结变形完成时，桩身轴力及桩侧摩阻力的计算值与实测值对比结果如图4和5所示，数据见表2.由图可知：最大轴力实测值与计算值近似相等，实测值中性点位置xn′=20.00 m，计算值xn=20.13 m，误差为0.65%；桩侧最大负摩阻力误差为2.33%.由此可见，本研究在计算考虑吹填土自重固结影响的桩基负摩阻力方面是有效的.

图4 深度-桩身轴力关系曲线计算值与实测值对比

图5 深度-摩阻力关系曲线计算值与实测值对比

表2 实测值与计算值对比

4 影响因素

4.1 桩顶荷载

待土层固结度达到90%后打设桩基.图6为不同桩顶荷载p下深度-轴力关系曲线.由图6可知：当桩顶荷载由0增加到200 kN时，桩身最大轴力从217.99 kN增大到325.36 kN，增大了49.25%；当桩顶荷载从400 kN增大到600 kN时，桩身最大轴力由455.16 kN增加到610.98 kN，增大34.23%.随着桩顶荷载的增加，轴力增大趋势逐渐变缓.

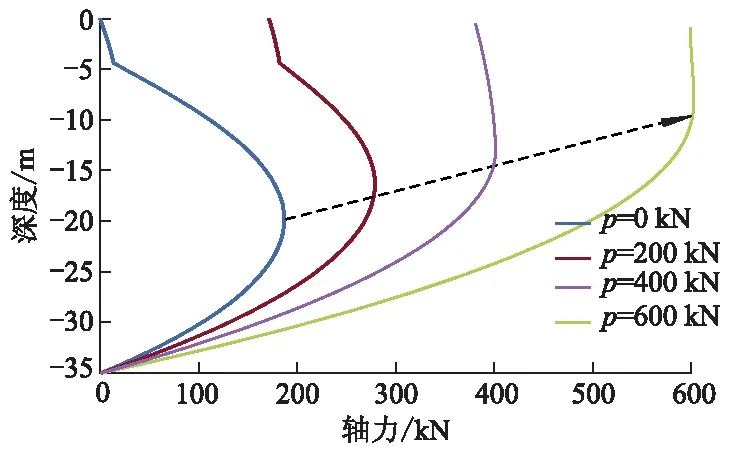
图6 不同桩顶荷载下深度-轴力关系曲线

图7为不同桩顶荷载下土层深度-摩阻力关系曲线.

图7 不同桩顶荷载下深度-摩阻力关系曲线

图6中的斜线表明不同桩顶荷载下桩身中性点位置的变化趋势.当桩顶荷载从0增加到600 kN时，中性点位置从20.13 m上升至7.88 m.可见随着桩顶荷载增大，中性点位置不断上移，也能从图7得到佐证，且桩顶荷载越大，其最大负摩阻力越小.原因在于桩周土的固结沉降不变时，桩顶荷载越大，桩身变形越大，桩土相对位移随桩顶荷载的增大而减小.表3为桩顶荷载对桩受力特性的影响.

表3 桩顶荷载对桩受力特性的影响

4.2 桩 径

图8为不同桩径D下深度-轴力关系曲线.图9为不同桩径下深度-摩阻力关系曲线.表4为不同桩径下桩的受力特性参数值.

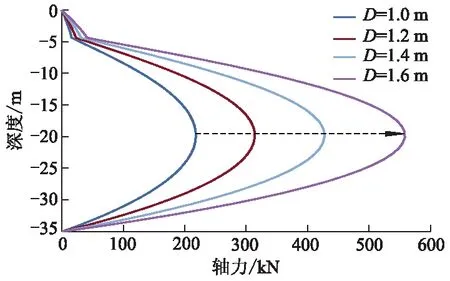
图8 不同桩径下深度-轴力关系曲线

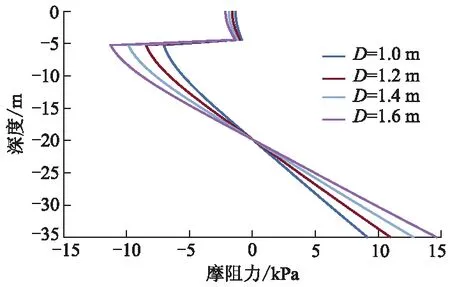
图9 不同桩径下深度-摩阻力关系曲线

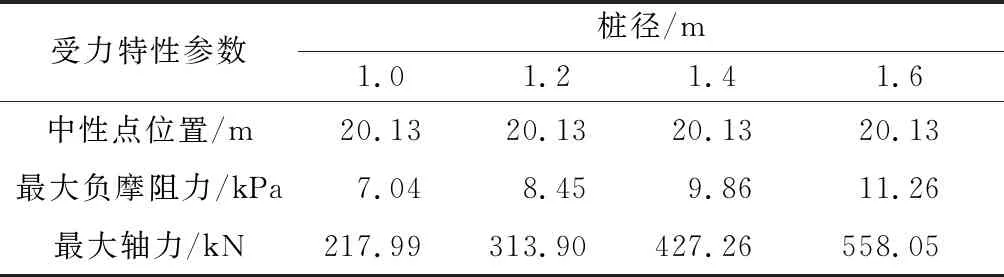
表4 桩径大小对桩的受力特性的影响

由图8、9及表4可知：当桩径从1.0 m增大到1.6 m时，最大负摩阻力由7.04 kPa增大到11.26 kPa，桩身最大轴力也由217.99 kN增加到558.05 kN，但桩身最大轴力的位置始终在20.13 m处，即中性点的位置并未因桩径的改变而发生改变.因此，在此问题中，其他条件不变的前提下，增大桩径对中性点的位置无影响，对于减小负摩阻力对桩基础受力特性的影响无作用.

4.3 固结时间和不同桩基打桩时间

图10为不同桩顶荷载下下拉荷载-固结度关系曲线.由图10可知：同一桩顶荷载下，下拉荷载随打桩时桩周土体固结度的增大而减小，且减小趋势渐缓，最后趋于稳定；在桩周土体相同固结度下打桩，桩顶荷载由100 kN增大到300 kN，下拉荷载由168.94 kN减小到87.36 kN.由此可见，在桩周土体相同固结度时打桩，桩顶荷载越大，下拉荷载越小，桩顶荷载的增大可有效地减小下拉荷载，其值越大，效果越明显.如果待桩周土体固结完成后再施打桩基础，桩周土体不会对桩产生下拉荷载.

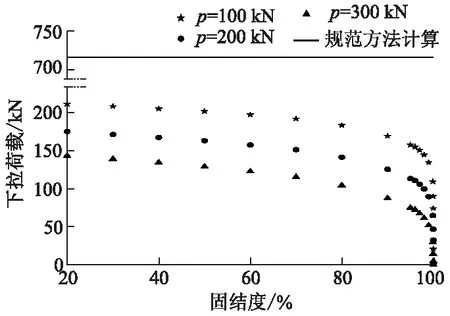
图10 不同桩顶荷载下下拉荷载-固结度关系曲线

依据JGJ 94—2008《建筑桩基技术规范》中的桩基础考虑负摩阻力影响的下拉荷载计算方法，得到该工况下桩体下拉荷载为710.62 kN.该方法在计算过程中没有考虑桩顶荷载的作用，同时也忽略了打桩前桩周土体已经发生的固结变形，这两方面因素都是减小负摩阻力的有利因素，故利用JGJ 94—2008计算的下拉荷载值远大于本研究计算值.

图11为不同桩顶荷载和固结度Ust下深度-时间因子关系曲线.当桩顶荷载相同时，打桩时桩周土体固结度越大，中性点位置越浅，最终趋于稳定.桩顶荷载越大，中性点位置上移速度越快.桩周土在相同固结度下打桩，桩顶荷载越大，中性点位置越浅.

根据JGJ 94—2008中经验法估算的中性点位置为28 m.该方法仍然未能考虑打桩前桩周土体已完成固结变形的影响，也未能反应桩顶荷载对中性点位置的影响.据经验法估算的中性点位置远大于计算值.致使JGJ 94—2008建议的计算方法过高估算了负摩阻力对桩基受力的影响，造成桩基础设计过长，造价增高.

图11 不同桩顶荷载和固结度下深度-时间因子关系曲线

5 结 论

1) 增大桩径并不影响中性点的位置.桩径增大，可以提高桩基承载力，但同时也使下拉荷载增大，故工程中有负摩阻力出现的情况下，采用通过桩径增大提高桩基承载力的措施时，需要考虑下拉荷载的影响.

2) 打桩前桩周土的固结度和桩顶荷载是减小负摩阻力的有利因素.桩顶荷载越大，负摩阻力越小，中性点的位置越浅，桩身受到总的下拉荷载越小；打桩前桩周土固结度越高，即打桩时间越晚，负摩阻力越小.

3) 桩周土在打桩前已完成的固结度和桩顶荷载对桩侧负摩阻力影响较大.由于JGJ 94—2008中对下拉荷载和中性点位置的估算未考虑这两方面因素，致使其过高估算了负摩阻力对桩基承载力的不利影响.