热变形参数对铸态SA508-3钢高温塑性的影响

武建国 安红萍 范盼飞

(太原科技大学材料科学与工程学院，山西030024)

SA508-3钢是一种含有Mo、Mn等元素的低碳合金钢，具有较高的淬透性、良好的冲击韧性和优良的焊接性能。广泛应用于核电设备一体化超大锻件的主体制造，如反应堆压力壳、稳压器、蒸汽发生器等[1]。此类锻件具有形状复杂，制造流程冗长等特点。尤其在自由锻过程中，钢锭内的铸态缺陷相对较多，经反复加热和显著的非均匀变形极有可能产生应力集中并形成微裂纹[2]。

本文采用Gleeble热模拟试验机在不同变形温度和应变速率下对铸态SA508-3钢进行等温拉伸试验，获得了不同变形条件下热拉伸试样的伸长率、断面收缩率等宏观塑性指标。为实现对变形过程中开裂行为的预测与控制，在有限元模拟中引入基于Normalized C-L断裂准则的损伤变量，通过高温拉伸与有限元模拟相结合的手段，从试样微区开裂的角度确定了相应的临界损伤量，该值可视为有限元损伤分析的微观塑性指标。研究结果可对评估铸态SA508-3钢的高温塑性提供宏观层面和微观层面的依据。

1 热拉伸试验

热拉伸试验所用铸态SA508-3的化学成分见表1。试样尺寸∅10 mm×121.5 mm，试验温度为800℃、900℃、1000℃、1100℃、1200℃；应变速率分别为0.001 s-1、0.01 s-1、0.1 s-1、1.0 s-1。采用Gleeble-1500D热模拟机进行等温拉伸，首先各试样均以10℃s的速度加热到1200℃，保温3 min，随后以10℃s的速度使试样降温至所需试验温度，以预定拉伸速度完成等温拉伸。在整个试验过程中采用氩气保护防止试件表面氧化。

2 试验结果分析

图1为铸态SA508-3不同温度和应变速率下的应力-应变曲线。研究认为，拉伸曲线上的峰值应力处对应着试样颈缩开始时刻[3]，试样内部在三向拉应力作用下萌生微小孔洞，进入损伤状态[4]。可以看到在同一应变速率下，随着变形温度的升高，峰值应力呈下降趋势，峰值应变逐渐减小，这是因为随温度升高，晶界间的强度会降低，试样在较低的形变量时就会有损伤萌生。从流变曲线的形状上可以看出，在较低的变形温度下应力达到峰值后急剧下降；而高温变形时，由于动态再结晶所引起的软化机制占主导作用，流变应力缓慢下降。在整个热变形条件下，应变速率越大，变形温度越低，材料的屈服强度及抗拉强度越大。

在材料力学性能指标中，断后伸长率和断面收缩率是衡量高温热塑性的重要特征值。图2、图3为铸态SA508-3钢的断后伸长率、断面收缩率与温度及应变速率的关系曲线，二者均随应变速率的增加而增加，但随着温度的增加呈现非单调变化特征。由图2可知，在较低应变速率下(0.001 s-1和0.01 s-1)，试样的断后伸长率在900～1000℃区间达到极值，随后在0.01 s-1应变速率下缓慢下降；而应变速率为0.001 s-1时断后伸长率随温度升高而下降至1100℃后又缓慢上升；在较高应变速率下(0.1 s-1、1 s-1)，断后伸长率在1100℃达到峰值，越过极大值后随温度升高缓慢下降。由图3可以看出除应变速率为1.0 s-1外，断面收缩率在1000℃达到极值后随温度上升缓慢降低；在1 s-1高应变速率下，变形温度高于1100℃时其断面收缩率接近100%。

图1 铸态SA508-3低合金钢应力-应变曲线Figure 1 Tensile stress-strain curves of as-cast SA508-3 low alloy steel

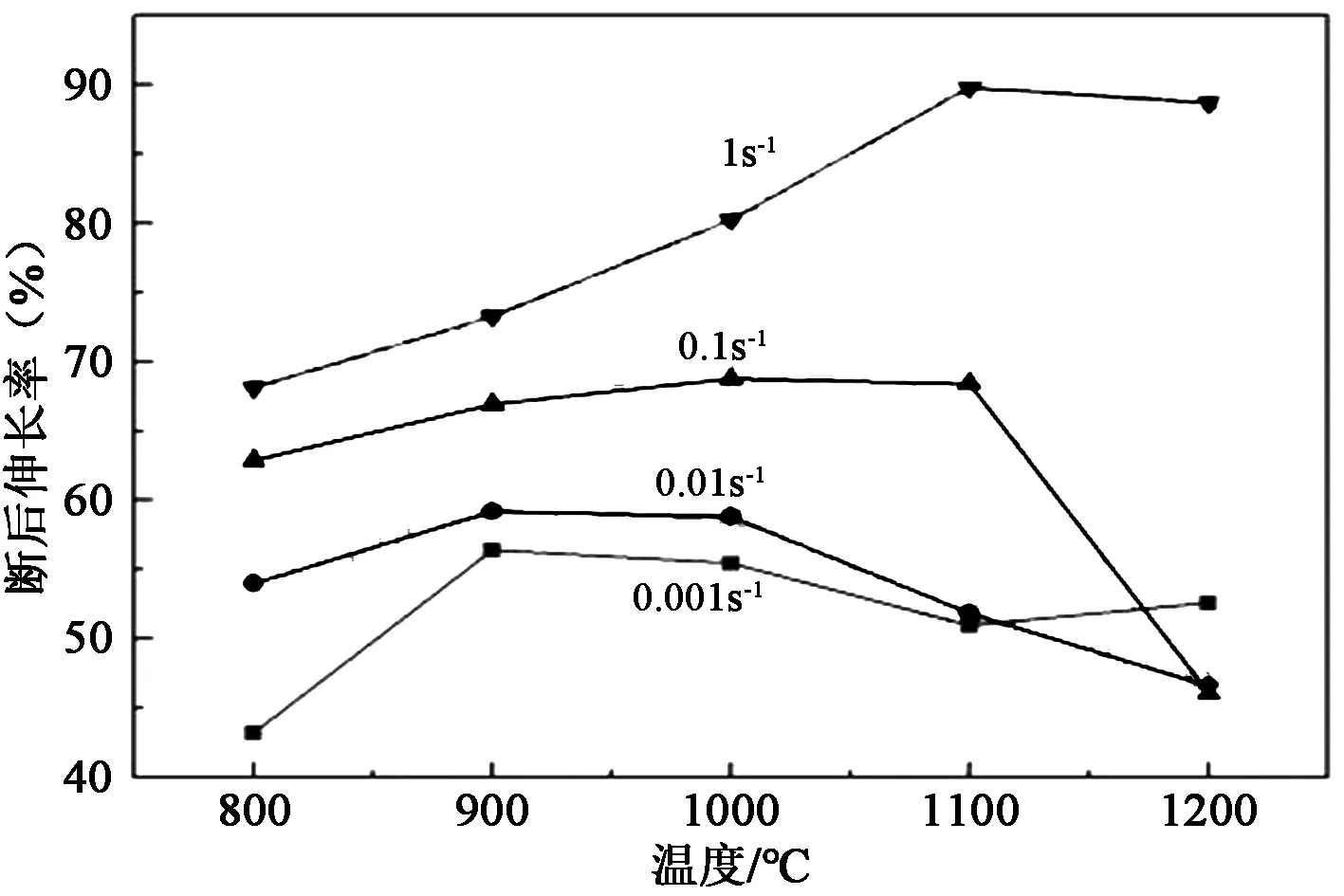
图2 热拉伸试样断后伸长率Figure 2 Elongation of thermal tensile specimens

图3 热拉伸试样断面收缩率Figure 3 Cross-sectional shrinkage of thermal tensile specimens

基于试验所得数据，通过回归分析可以将断后伸长率、断面收缩率表达为温度及应变速率的函数：

3 临界损伤值

断后伸长率与断面收缩率，作为常用的宏观指标能方便地用于评价材料的高温塑性。但是，对于热加工过程而言，锻件内部塑性的相对变化以及开裂风险的评估往往需要借助于有限元模拟来获得。将Normalized C-L准则引入有限元模拟中可以描述拉应力状态下锻件内的损伤水平和开裂风险。该准则可以表达为[5]：

当累积的损伤值到达临界值时，就会产生局部开裂。因此，临界损伤值是评估锻件开裂风险的关键因素，该值很难直接从试验中获得，但可以通过有限元模拟与拉伸试验数据相结合的方法确定。

首先，通过有限元软件DEFORM建立一个合理的热拉伸模型，在前处理系统中将SA508-3钢的高温流变行为赋予变形体，同时指定正确的变形温度，并根据试验条件在变形体上表面施加合理的拉伸速度。完成热拉伸模拟，输出相应的载荷-位移曲线，并与试验中获得的载荷-位移曲线进行比较，相对误差较小时，说明模拟结果较为准确。当模拟试样的断后伸长率等于相同变形条件下实测的断后伸长率时，获得该时刻模拟试样最小横截面外半径处的损伤值，即为既定变形条件下的临界损伤值。将该值输入DEFORM系统，则可完成热拉伸试样的断裂模拟。

图4 热拉伸模拟结果Figure 4 Simulation results of thermal tensile test

图5 拉伸过程中裂纹的形成与扩展Figure 5 Crack formation and propagation during tensile deformation

图6 临界损伤值与温度及应变速率的关系Figure 6 Relationship between critical damage values and temperature and strain rate

图4(a)所示为温度1200℃，应变速率0.01 s-1时的模拟结果，模拟试样与试验试样具有相同的形状与尺寸。由图4(b)可知，变形过程中试样颈缩区的损伤程度不断增加，一旦达到该条件下的临界值，则相应的微裂纹就会出现。如图5所示，拉伸过程中试样内部微裂纹的形成、扩展直至试样断裂的过程通过边长为0.2 mm的细小单元精确地反应出来了。在图5的局部放大图中，杯锥状的宏观断口形貌也得以清晰呈现。由此可见，临界损伤值其实相当于一个微区材料分离准则，因此可将临界损伤视为基于有限元模拟的微观塑性指标。采用上述方法可以得到不同温度不同应变速率下的临界损伤值，其随温度与应变速率的变化趋势如图6所示。通过数据回归，临界损伤值可以表达为温度及应变速率的函数。

4 结论

(1)通过高温拉伸试验，得到了SA508-3钢断后伸长率和断面收缩率随温度和应变速率的变化规律：断后伸长率和断面收缩率均随应变速率增大而增大；但随温度增加都呈现非单调变化特征。通过数据回归分析，可以确定断后伸长率、断面收缩率与温度及应变速率之间的定量关系：

(2)高温拉伸试验结合有限元模拟，确定了热变形过程中SA508-3钢在拉应力作用下的临界损伤值，该值代表了高温变形时锻件内部的微区开裂条件。通过数据回归分析，可以获得临界损伤值与温度及应变速率之间的定量关系：