如何正确运用Z检验——两总体率比较优效性Z检验及SAS实现

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

虽然统计分析方法多种多样，但临床科研工作者最常用的分析方法是一般差异性检验［1-2］。为了使假设检验的结果不仅具有统计学意义，还具有临床实际意义，在处理临床资料时常需要选用3种特殊的差异性检验，即非劣效性检验、等效性检验和优效性检验［3］。本文将结合临床实际，介绍与“两总体率比较优效性检验”有关的内容。

1 两总体率比较优效性Z检验的基本原理和方法

1.1 基本概念

优效性检验是指主要研究目的为显示试验药的治疗效果优效于对照药（安慰剂对照或阳性对照）的试验。在试验设计阶段需要设定一个界值δU，来界定试验药的优效性［3-4］。

1.2 问题与数据结构

【例1】为观察复方薤白胶囊治疗慢性支气管炎急性发作期痰热郁肺证的效果。随机选取240例符合要求的患者，均分为2组，试验组口服复方薤白胶囊，对照组口服芩暴红止咳胶囊，疗程均为10 d。两组的有效率分别为96.67%（有效例数n=116）和92.50%（有效例数n=111），如果试验组的有效率超过对照组5%，才能认为复方薤白胶囊优效于芩暴红止咳胶囊，试评价复方薤白胶囊是否优效于芩暴红止咳胶囊［5］。临床资料见表1。

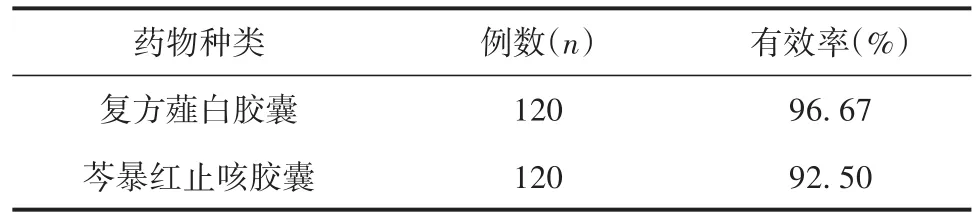
表1 两组患者的治疗效果

【对数据结构的分析】该资料的试验因素为“药物种类”，其两个水平分别为“复方薤白胶囊”与“芩暴红止咳胶囊”，观测指标为“有效率”，所以该资料为成组设计一元定性资料。

【统计分析方法的选择】研究者的研究目的是评价复方薤白胶囊治疗慢性支气管炎急性发作期痰热郁肺证的效果是否优效于芩暴红止咳胶囊治疗效果，并且设定了优效性界值δU=5%，这时应选用优效性检验。

【例2】某一临床试验中观察某新药A对某种肿瘤临床症状的控制效果，以某标准药物B作对照行随访研究。所有患者同时入组，观察期为1年，主要评价指标为症状改善率。临床资料见表2，如果设定优效性界值为6%，试判断药物A是否优效于药物B。临床资料见表2。

表2 两组患者的症状改善情况

1.3 基本原理

1.3.1 检验假设

给出检验假设，并规定检验水准α的值。

H0：πT-πR≤δU；

H1：πT-πR＞δU；

α=0.05（单侧）。

1.3.2 检验统计量

所需要的检验统计量如下式：

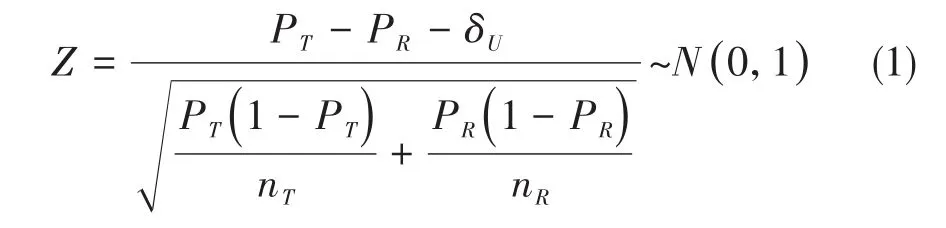
拒绝域为Z＞Z1-α。

在式（1）中，检验统计量Z服从标准正态分布；（PT、nT）与（PR、nR）分别为试验组（T）与对照组（R）的“样本率、样本含量”；δU为优效性界值。

1.3.3 基于检验统计量Z的取值计算单侧尾端概率

根据检验水准查表或借助相应的SAS函数进行计算，获得检验统计量Z的临界值（针对手工计算而言）和（或）标准正态分布尾端的概率（针对统计软件而言）。

1.3.4 得出统计学结论和专业结论

根据拒绝还是不能拒绝H0的结果，给出统计学结论，最后结合专业知识给出专业结论。

2 两总体率比较优效性检验的SAS实现

2.1 基于SAS语言按公式编程间接实现计算

基于SAS语言和标准正态分布函数等知识［6］并按式（1）进行编程，就可间接实现两总体率比较优效性Z检验。

SAS程序如下：

【程序说明】变量名后面的“_t”与“_r”分别代表“试验组”与“对照组”相应的量（包括样本含量与有效率）；有效率用6位小数表示的目的是使计算结果尽可能精确一些，这样就与后面基于FREQ过程直接计算的结果具有一定的可比性。

【SAS输出结果】

【统计学结论】因Z=-0.28639，P=0.61271（单侧概率）＞0.05，所以，应接受H0。

【专业结论】在优效界值δU=5%的前提条件下，尚不能认为复方薤白胶囊治疗慢性支气管炎急性发作期痰热郁肺证的效果优效于芩暴红止咳胶囊的治疗效果。

2.2 基于SAS中FREQ过程直接实现计算

由于SAS中FREQ过程包含了几乎绝大多数定性资料假设检验方法［7］，所以，此处将采用此过程来直接实现两总体率比较优效性Z检验。

SAS程序如下：

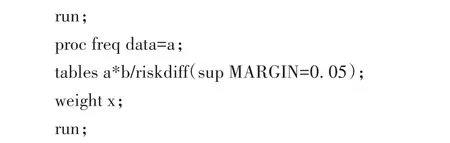
【程序说明】各组中的数据应为“有效例数”与“无效例数”，而不适合直接采用“有效率”；程序中sup表示进行优效性检验；MARGIN=0.05表示优效界值。

【SAS主要输出结果及解释】

因Z=-0.2864，P=0.6127，说明尚不能认为复方薤白胶囊治疗慢性支气管炎急性发作期痰热郁肺证的效果优效于芩暴红止咳胶囊的治疗效果。若利用置信区间来判断，由计算结果可知：两有效率之差的90%置信区间为［-0.0062，0.0895］，因置信区间包含δU=0.05，说明优效性结论不成立。

3 讨论与小结

3.1 讨论

3.1.1 影响优效性检验结果的因素

3.1.1.1 概述

优劣效性检验结果不是绝对的，随着条件的改变，最终的检验结果也会发生相应的改变，影响其结果的因素有“显著性水平α”“优效性界值δU”和“样本含量”。

3.1.1.2 α的取值对优效性检验结果的影响

优效性检验结果不是绝对的，与显著性水平α的取值有密切关系。现以本文例2数据为例，若取显著性水平α=0.05，δU=6%，得到的计算结果为Z=1.7925，P=0.0365（单侧概率）＜α=0.05，即可以认为药物A优效于药物B。若取显著性水平α=0.025，δU=6%，得到的计算结果为Z=1.7925，P=0.0365（单侧概率）＞α=0.025，即不能认为药物A优效于药物B。

3.1.1.3 δU的取值对优效性检验结果的影响

优效性检验结果与优效性界值δU的取值有密切关系。现以本文例2数据为例，若取显著性水平α=0.05，δU=6%，得 到 的 计 算 结 果 为Z=1.7925，P=0.0365（单侧概率）＜α=0.05，即可以认为药物A优效于药物B。若取显著性水平α=0.05，但取δU=10%，得到的计算结果为Z=1.1361，P=0.1280（单侧概率）＞α=0.05，即不能认为药物A优效于药物B。

3.1.1.4 样本含量对优效性检验结果的影响

现以本文例2数据为例，若取显著性水平α=0.05，δU=6%，若直接按表2中的数据进行优效性检验，其结论为“药物A优效于药物B”。若将各组的样本含量各减少一半，即A药物组有效例数为41例（有效率为62.12%）、无效例数为25例；B药物组有效例数为30例（有效率为45.45%）、无效例数为36例，基本保持两组的有效率分别与表2中的接近。此时，优效性检验的结果为Z=1.2466，P=0.1063（单侧概率）＞α=0.05，即不能认为药物A优效于药物B，与前面的结论正好相反。需注意的是，在拟开展优效性试验研究之初期，就应当按照已知的条件［包括两组估计的有效率、显著性水平α的值、检验效能（1-β）的值和优效性界值δU的值］，找到相应的计算公式，估计出合适的样本含量［3］。

3.1.2 主要疗效评价指标的临床意义

在进行优效性检验时，一个常被忽视的问题是评价指标的临床意义。具体地说，就是应明确当前的评价指标究竟属于“高优指标（指标取值越大越好，如治愈率）”还是“低优指标（指标取值越小越好，如死亡率）”。当面对高优指标时，通常情况下，试验组指标的取值高于对照组指标的取值时才适合考虑选用“优效性检验”；如果在较大样本含量的预试验中，已获得的试验结果是“试验组指标的取值明显低于对照组指标的取值”，若此时仍坚持选用“优效性检验”就不太符合常理了。按正常思维，此时应当考虑选用“非劣效性检验”或“等效性检验”。

3.1.3 δU是否总是取正值

在进行优效性检验时，统计学教科书上通常都默认把δU取为“正值”，代表试验药疗效比对照药疗效“好”。事实上，这样做有一个隐含的前提，即疗效的评价指标为“高优指标”。而当疗效的评价指标为低优指标时，若拟采用优效性检验，此时，其优效界值δU应取负值。

3.2 小结

本文介绍了两总体率比较优效性Z检验的原理、方法和SAS实现。在SAS实现方面，介绍了基于SAS语言编程间接实现两总体率比较优效性Z检验以及基于SAS中FREQ过程直接实现与前面提及的相同计算。在后者中，还给出了两总体率之差的置信区间。基于置信区间也可以判断优效性结论是否成立。