基于圆周拉普拉斯算法的机械零件边缘检测方法研究*

戴乔森，何毅斌，陈宇晨，刘 湘，贺苏逊，吴琳慧，杜 伟，汪 强

(武汉工程大学 机电工程学院，湖北 武汉 430073)

0 引 言

在现代机械制造业中，机械零件是否符合生产要求离不开零件尺寸的精度检测[1]。而测量机械零件的尺寸首先就要得到其清晰、完整的边缘轮廓，而通过计算机视觉的方式获得零件边缘是近几年研究的重点。

相较于传统的测量方法，计算机视觉拥有速度快、精度高、不易受到人为因素影响的优势，并逐渐被各大机械相关研究机构所采用。

边缘检测算法有很多，根据计算边缘导函数类型的不同，可以将边缘检测算法分为一阶导函数和二阶导函数两类[2]。通常情况下，一阶导函数对边缘定位速度快且节约检测时间；二阶导函数相对复杂但效果更好[3]。拉普拉斯算法以二阶微分算法为基础，因其各项同性的特点，即将图像旋转后滤波与先对图像滤波再旋转结果相同而得到更广泛的应用。对于图像边缘的基本特征识别，由于采集到的原始图像质量会受到环境因素、物体表面等不可控因素的影响[4]，在实际处理时需要人为消除不利因素对图像的影响。

国内外学者对于应用拉普拉斯算法提高边缘检测的精度和效率做了许多研究和改进：文献[5]在传统拉普拉斯的基础上添加了变量sigma用于确定两个方向上的高斯核以增强图像边缘轮廓的清晰度，但计算时间长，导致边缘线条较为粗糙；文献[6]提出了改进的log算子与ViBe算法相结合的阴影消除算法，从而提高了阴影消除方法的综合性能和鲁棒性，但算法过于繁琐，并不具备高效性的特点；文献[7]提出了基于数学形态学的齿轮边缘提取方法，但是经过具体实验可知该方法不具备普遍性。

笔者提出一种圆周拉普拉斯算法，目的是在保证算法高效性的同时，提高边缘检测的清晰度和细节的完整性，并加入数学形态学中的顶帽变换和底帽变换，以保证图像的抗噪性。

1 拉普拉斯算法

一个二维图像函数的拉普拉斯算法定义为:

(1)

对于离散二维图像，可以用下式作为对二阶偏微分的近似:

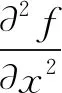
(2)

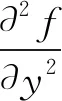
(3)

将上面两式相加就得到用于图像锐化的拉普拉斯算法:

▽2f=[f(i+1,j)+f(i-1,j)+f(i,j+1)+f(i,j-1)]-4f(i,j)

(4)

这个公式可以由以下滤波模板来实现:

分析拉普拉斯算法模板的结构可知，这种模板对于90°的旋转是各向同性的。更进一步，还可以得到如下对于45°旋转各向同性的拉普拉斯算法模板[8]:

2 圆周拉普拉斯边缘检测算法

2.1 圆周拉普拉斯算法

笔者在1节中对传统的拉普拉斯算法模板生成原理进行了分析，接下来将在此基础上对其进行改进。

图像I在经过旋转、平移、缩放后，可得到图像I′，即：

I′=k·S·I+β

(5)

式中：k—图像缩放的比例，是标量；S—旋转矩阵；β—图像偏移量。

变换后图像上各点坐标对应关系为：

(6)

求一阶导数可得：

(7)

式中：Iu—图像在u方向的偏导数；Iv—图像在v方向的偏导数。

将矩阵窗函数变成一维向量，变换后的公式如下所示：

(8)

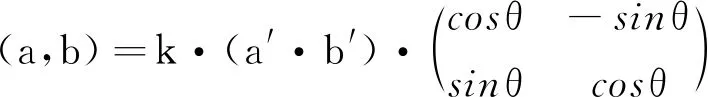
(9)

式中：M—原图像的相关矩阵；a—Iu加权后的一维向量；b—Iv加权后的一维向量；a′，b′—变换后的a，b向量。

原图像的相关矩阵为：

(10)

将式(8，9)代入式(10)中可得：

(11)

图像变换后的灰度相关性为：

(12)

故图像经变换后的灰度矩阵为：

(13)

当k=1时，图像仅进行平移和旋转，变换前后矩阵M是相似的，故平移和旋转对判别式没有影响；

当k≠1时，即图像缩放，M不相似，故传统的拉普拉斯算法不具有不变性。

传统的拉普拉斯算法和圆周算法模板的对比如图1所示。

图1 传统拉普拉斯算法模板和圆周拉普拉斯算法模板

由图1可知：传统的拉普拉斯算法一般选用3×3的模板进行滤波，在传统的算法中，由于拉普拉斯算法的模板为矩形；当图像发生旋转时，必然会影响边缘检测的准确性。

本文提出圆周拉普拉斯算法模板，通过圆周上像素点来确定图像边缘；由于圆周上各点到中心点距离相等，当图像发生旋转时，圆周上的点不会发生变化，进而边缘检测的准确性也不会受到影响。

因此，笔者提出的圆周拉普拉斯算法模板具有旋转不变性。

2.2 数学形态学去噪法

由于锐化算法的作用是突出图像的细节，但并不能区分图像中有效的边缘和无效的噪声，在实际应用中通常不单独使用。由于数学形态学不仅能消除图像的噪声，还能做到不破坏图像边缘的细节[9]。

笔者算法将结合灰度级形态学中的顶帽变换和底帽变换，对已经提取到的零件边缘进行优化。

2.2.1 灰度级形态学腐蚀

灰度级形态学腐蚀定义如下:

(14)

式中：b—非平坦结构元；f—原图像相关矩阵。

2.2.2 灰度级形态学膨胀

灰度级形态学膨胀的定义如下:

(15)

式中：b—非平坦结构元；f—原图像关矩阵。

2.2.3 灰度级形态学的开操作和闭操作

灰度级形态学腐蚀的定义如下：

f∘b=(fΘb)⊕b

(16)

式中：b—非平坦结构元；f—原图像关矩阵。

具体含义是先用结构元b对图像f做腐蚀，随后用结构元b对所得结果进行膨胀。同理，结构元b对图像f的闭操作表示为f·b，即：

f·b=(f⊕b)Θb

(17)

式中：b—非平坦结构元；f—原图像关矩阵。

开操作用来平滑物体的轮廓、断开窄狭颈并消除较细的突出物。比操作用来连接窄间断和长沟壑，消除小的孔洞，填补轮廓线中断裂的区域。

2.2.4 灰度级形态学的顶帽变换和底帽变换

由式(14～17)可以组成绘图形态学的top-hat(顶帽)变换和bottom-hat(底帽)变换[10,11]。灰度级图像f的顶帽变换指的是f减去其开操作，即：

That(f)=f-(f·b)

(18)

同理，灰度级图像f的底帽变换指的是f的闭操作减去f，即：

Bhat(f)=(f·b)-f

(19)

在圆模板拉普拉斯算法边缘检测图像上，加上顶帽变换再减去底帽变换，就可以在不增加运算复杂度的情况下有效地抑制噪声，从而提高图像的有效信息。

3 实例分析

实验采集到的齿轮零件图和手表零件图如图2所示。

图2 实验零件图

实验中，使用了两种传统拉普拉斯算法和笔者提出的圆周拉普拉斯算法进行对比，其结果如图3所示。

图3 传统拉普拉斯算法与拉普拉斯圆周算法的实验效果

图3(b，f)是使用传统拉普拉斯算法中90°各项同性的模板对齿轮和零件图进行锐化的实验效果图；

图3(c，g)是使用传统拉普拉斯算法中45°各项同性的模板对齿轮和零件图进行锐化的实验效果图；

图3(d，h)是使用本文提出的圆周拉普拉斯算法模板进行锐化的实验效果图。

对零件边缘提取结果放大的图如图4所示。

图4分别是90°各项同性模板、45°各项同性模板、圆周拉普拉斯算法模板对齿轮零件进行实验结果的局部放大图。

对比3种算法的实验结果可以看出：传统拉普拉斯算法对于提取的零件边缘存在不连续、不清晰的缺陷，而使用圆周拉普拉斯算法提取出的零件边缘则更加连续，细节保留地更加完整。

从图3(d，h)可以看出：仅使用圆周拉普拉斯算法并不能去除图像中的噪声。因此，为了得到更符合实际生产需要的边缘轮廓图，还需要对图像进行去噪。

采用数学形态学中的顶帽变换和底帽变换的结果如图5所示。

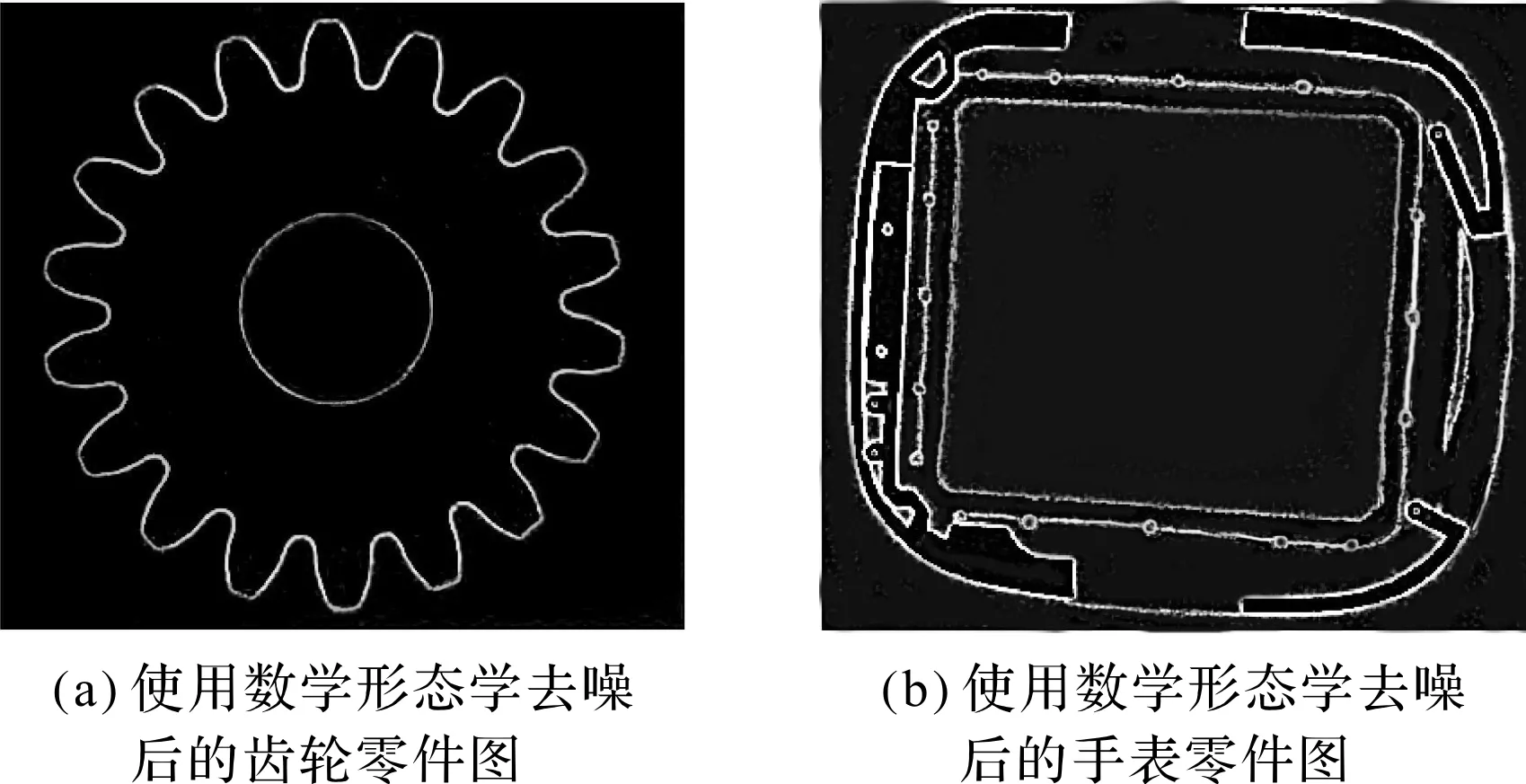
图5 使用数学形态学去噪的效果最终效果图

由图5可以看出，使用数学形态学去噪后，图像中的噪声得到了明显的抑制。

峰值信噪比(PSNR)作为一种评价图像质量的检测方法，因其普遍适用的特性而被广泛运用在各种实验中；且其值越大，被证明其检测效果越好，算法越优秀。

笔者分别对齿轮零件和手表零件的3种算法的实验过程进行了计算，其对应的峰值信噪比得到的结果如表1所示。

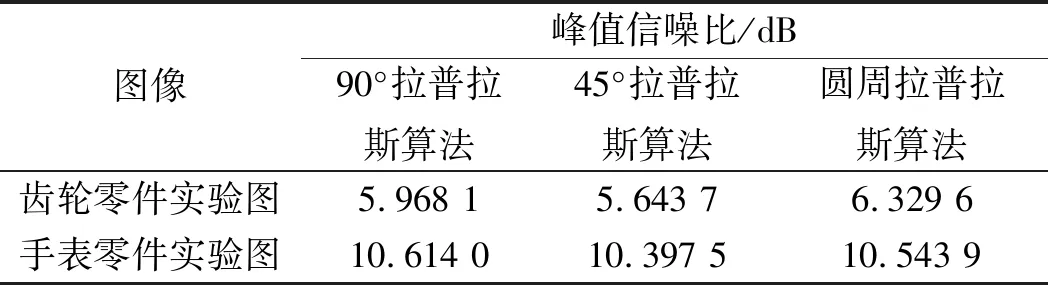
表1 图像边缘检测效果评价表

从表1中可以看出：圆周拉普拉斯算法的峰值信噪比比传统算法更大，说明笔者提出的算法起到了改进的作用。

从该实验结果可以看出：

(1)传统拉普拉斯算法在检测机械零件边缘上存在清晰度不足、细节失真等问题，且由于其旋转不变性，圆周拉普拉斯算法可以有效地避免这点；运用圆周拉普拉斯算法检测出的零件边缘更接近真实情况；

(2)在应用圆周拉普拉斯算法边缘检测的机械零件图像上，加上数学形态学的顶帽变换和底帽变换，可以在不影响图像边缘细节的前提下，有效地抑制噪声。

4 结束语

通过传统的边缘检测算法得到的图像往往存在边缘不连贯和细节缺失的问题，提取的边缘效果不理想。

针对传统算法的这类缺陷，笔者提出了一种圆周拉普拉斯算法，并采用了常见的齿轮和手表零件进行了实验验证。实验结果证明，圆周拉普拉斯算法方法能够完整地保留机械零件图像中的边缘信息，能更有效地还原图像边缘的有效信息；同时，加入了数学形态学中的顶帽变换和底帽变换进行去噪处理，可以去除图像中的无效信息，得到噪声少、边缘曲线连续、清晰、图像信息保留完整的零件图像。

最后，笔者采用峰值信噪比法，对传统算法与圆周拉普拉斯算法进行了对比，其结果证明，笔者所提出的算法更为优秀。