基于欠驱动原理的多指灵巧手结构设计及实验研究*
宋振东,李 刚,武 桐,王玉娟,何元一
(1.深圳职业技术学院 机电工程学院,广东 深圳 518055;2.沈阳新松机器人自动化股份有限公司 中央研究院, 辽宁 沈阳 110169;3.哈尔滨工业大学(深圳) 实验与创新实践教育中心,广东 深圳 518055)
0 引 言
多指灵巧手是一种具有多个手指、能够完成各种复杂抓取动作的机械手装置,在工业、国防、医疗康复等领域均具有十分广泛的应用前景。
世界上最早的灵巧手是美国科学家TOMOVIC和BONI于1962年研制的Belgrade灵巧手,采用弹簧片进行驱动,主要目的是替换士兵的伤残手。Belgrade只能完成一些简单的夹持操作[1]。真正意义上的多指灵巧手是1974年由日本科学家研制,被称为Okada[2]。Okada具有3根手指和1个手掌。Okada采用电机作为驱动,利用钢丝进行传动。Okada手指细长,其所能承担的负载较小,且无法感知目标物体的位姿,也不能自动控制夹持力。此后,国外科学家相继研发了多种多指灵巧手,如美国麻省理工研发的Utah/MIT四指灵巧手[3,4]、美国斯坦福大学研发的Stanford/JPL三指灵巧手[5]等。这个阶段的多指灵巧手在结构方面有了巨大突破,具有多个自由度,也搭配了一些简单的传感器,但仍然不能动态感知抓取的目标物体的位姿变化,在抓取力的控制上也比较粗糙。
随着电子技术及传感技术的不断发展,多指灵巧手随后进入到了一个新阶段,如德国宇航中心研发的DLR四指灵巧手[6]、美国国家航空宇航局研发的Robonaut2五指灵巧手[7]、日本歧阜大学研发的Gifu系列多指灵巧手[8]、英国SHADOW公司研发的Shadow五指灵巧手[9]等。这个阶段的多指灵巧手均具有多个自由度,并搭配了多种传感器,可以完成许多复杂的抓取任务。其中,DLR是电机驱动的代表,SHADOW是气动人工肌肉驱动的代表,Robonaut2是腱传动驱动的代表。SHADOW一般用于实验研究,只有DLR及Robonaut2具有真正的拟人特性用于应用。由于这个时期的灵巧手机械结构及传感器技术比较成熟,问题主要集中在重量上[10]。
我国对于多指灵巧手的相关研究起步较晚,且成果主要集中在高校及科研机构。最早的国产多指灵巧手是由北京航空航天大学1993年研制的,这是一种三指灵巧手,称BUAA-Ⅰ。北航后续相继研发了BUAA-Ⅱ、BUAA-Ⅲ[11]。相比初代BUAA灵巧手,BUAA-Ⅱ、BUAA-Ⅲ具有更多的手指及自由度,功能也更加完善。另一具有代表性的国产多指灵巧手为哈尔滨工业大学研制的HIT Hand系列灵巧手,该系列灵巧手具有多个自由度,可以完成多种目标物体的抓取[12-14]。这些灵巧手由于具有多个自由度,导致驱动源数量较多、机体结构复杂、重量较大;且由于安装了多种昂贵的传感器,导致成本居高不下,很难推广和应用,绝大多数还停留在实验室阶段[15]。
目前,大多数已经研制的灵巧手由于具有多个自由度,导致灵巧手结构十分复杂,具有多个驱动源,然而复杂系统在增加灵巧性的同时,也增加了控制系统的难度。在抓取物体的过程中,灵巧手需要感知目标物体与执行器之间的作用力,而这种触觉传感器价格十分昂贵,直接影响多指灵巧手的应用和推广。另外,在抓取目标物体的过程中,由于驱动手指的驱动电机不具备反向自锁功能,绝大多数灵巧手处于一种动态监测抓持力的循环中,系统中的电机持续运转,严重缩短了电机的使用寿命,提高了灵巧手维护和保养的成本等。
针对以上问题,综合分析现有多指灵巧手结构,基于自适应抓取原理,本文提出一种具有欠驱动特性和自锁特性的双关节灵巧手手指结构方案。
1 多指灵巧手手指结构设计
目前,绝大多数灵巧手手指采用多驱动源、多自由度的设计方案,使得手指结构复杂、重量较大。由于自由度较多,手指各关节无法实现反向自锁,在执行抓取任务时,关节电机需要处于使能状态,长时间运行导致电机发热明显。
本文提出一种具有欠驱动特性和自锁特性的的双关节灵巧手手指结构方案。该方案采用具有反向自锁功能及大传动比的蜗轮蜗杆机构作为手指的主要传动机构,搭配有刷伺服电机、齿轮传动组及绳传动组,实现双关节手指的各项功能。
手指结构设计如图1所示。

图1 手指结构设计
图1中,驱动电机通过转动输出轴,带动轴端齿轮G1转动,齿轮G1与齿轮G2啮合,因此齿轮G2随之转动;齿轮G2同时与齿轮G3、G4啮合;齿轮G3驱动蜗轮蜗杆传动组W1,G4驱动蜗轮蜗杆传动组W2,两传动组速比相同,为i4。
由于W1中蜗轮与指节固连,其旋转角速度ω1为:
ω1=ω0i1i2i4
(1)
式中:ω0—齿轮G1转速;i1—齿轮G1与齿轮G2传动比;i2—齿轮G2与齿轮G3传动比;i3—齿轮G2与齿轮G4传动比。
由于W2中蜗轮通过转动带动钢丝绳运动,从而实现对末端关节的驱动,其传动比为i5。因此,末端关节的旋转角速度ω2为:
ω2=ω0i1i3i4i5
(2)
式中:i4—蜗杆传动组W1及W2传动比;i5—钢丝绳传动比。
因此,手指指根关节与末端关节的运动耦合关系为:
ω1/ω2=i2/(i3i5)
(3)
在手指结构中,i2=0.52,i3=0.62,i5=1.11,因此ω1/ω2=1/1.326。根据结构设计原理,本文设计的灵巧手手指指根关节运动范围为0°~140°,末端关节运动范围为0°~45°。
为了能够使灵巧手对不规则形状的目标物体进行自适应抓取,本文对灵巧手手指结构进行了欠驱动设计。在抓取过程中,手指的指根部分首先接触物体,此时驱动电机输出扭矩上升,继续驱动指根关节及末端关节转动。由于齿轮与齿轮轴是采用螺纹进行固定的,蝶形弹簧对齿轮施加推力,使齿轮中心内螺纹与齿轮轴表面外螺纹之间产生足够的摩擦力。当扭矩达到碟形弹簧的预压扭矩后,齿轮中心内螺纹与齿轮轴表面的外螺纹之间的压力降为零,齿轮将会脱出,则电机会继续带动末端指节进行转动,实现手指欠驱动设计。这种情况可以确保灵巧手对不规则形状进行适应性抓取。
手指末端关节采用腱传动方式,通过位于指根处的末端驱动蜗轮带动钢丝绳运动,钢丝绳带动末端关节转动。笔者在指节内部设计钢丝绳张紧机构,保证钢丝绳具有足够的刚度。对于灵巧手手指末端,常用的传动结构还有齿轮传动、带传动、连杆传动等方式。然而,齿轮传动在狭小空间内布局困难,设计复杂;带传动刚度太差,不利于运动精度的实现;连杆传动的缺点在于不能准确地控制其传动比,难于实现精确控制。相比之下,采用钢丝绳传动的方式,具有空间小、刚度大、传动比恒定的特点,易于实现精确控制。
腱传动方案中,钢丝绳采用7×7规格的钢丝绳,钢丝绳直径0.5 mm。对于需要更大复杂的多指灵巧手,可以采用直径更大的钢丝作为传动钢丝。
由于钢丝直径变大,导致钢丝具有更大刚度,此时需要张紧机构具有更大的张紧力,为此,本文提出了具有较大张紧力的腱传动结构方案。
低载版及高载版腱传动机构如图2所示。

图2 腱传动结构方案
高载版腱传动机构中,主动端通过锁紧在钢丝绳上的金属卡扣,卡在主动轮(蜗轮)卡槽内。被动端钢丝绳穿过安装孔,通过锁紧螺丝及铜柱压紧。该结构可以实现钢丝绳的快速安装且固定可靠。张紧机构为连杆结构,利用曲柄滑块原理,可调节钢丝绳支撑角的大小,从而实现钢丝绳的连续张紧。
由于本文设计的灵巧手指主要采用了蜗轮蜗杆传动、齿轮传动及腱传动,由该手指组成的多指灵巧手传动效率主要受以上3种传动机构的效率影响。
其中,齿轮传动为两级圆柱齿轮传动,其效率η1约为:
η1=0.95×0.95=0.902 5
(4)
腱传动的效率η2约为0.96。对于蜗轮蜗杆传动,蜗杆切向力Ft1为:
Ft1=2 000T/d1
(5)
式中:T—周向扭矩;d1—涡杆分度圆直径。
涡轮切向力Ft2为:
(6)

蜗轮蜗杆的传动效率η3为:
(7)
根据以上计算结果,手指的传动效率η为:
η=η1η2η3=0.295
(8)
系统总传动比i为:
i=i1i2i3i4=2.17×1.615×50×0.9=157.7
(9)
式中:i1—齿轮组1传动比;i2—齿轮组2传动比;i3—涡轮蜗杆传动比;i4—钢丝传动比。
因此,手指末端输出扭矩T为:
T=T1iη
(10)
式中:T1—电机输出扭矩。
2 多指灵巧手构型设计
2.1 二指灵巧手结构设计
二指灵巧手由两个相对布置的模块化手指及手腕组成,两个手指独立驱动。与全驱动的灵巧手结构不同,本文设计的灵巧手指由于进行了欠驱动结构设计,手指具有欠驱动的运动特性,不但可以对不同形状的目标物体进行自适应抓取,而且具有更好的鲁棒性,手指结构及运动被干扰的程度大大降低。
二指灵巧手结构模型如图3所示。
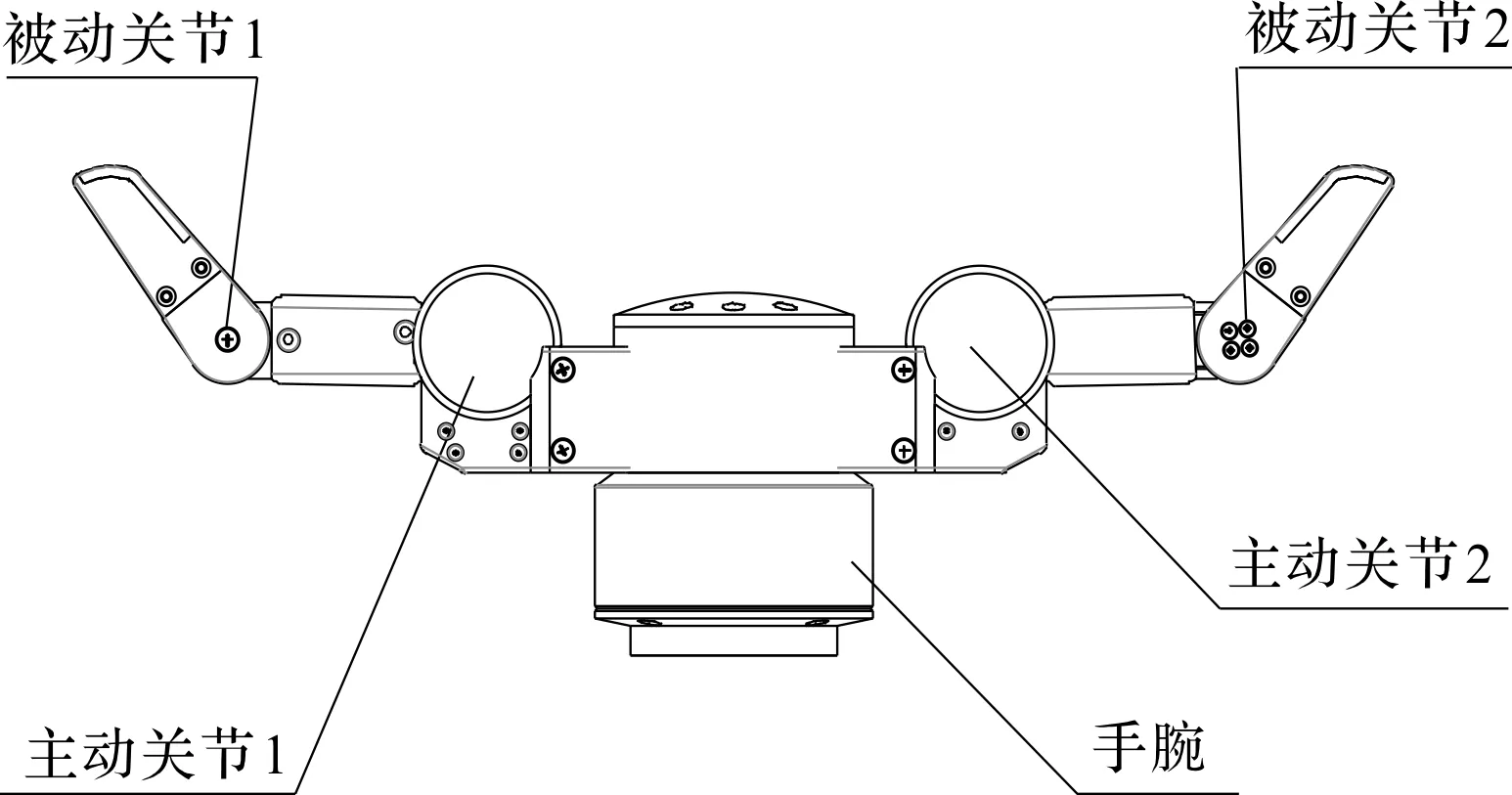
图3 二指灵巧手结构模型
图3中,全手共具有4个关节,其中2个主动关节1、2,2个被动关节1、2。对于手指而言,主动关节与被动关节通过耦合机构,可以按照一定的角度关系进行运动。
2.2 三指灵巧手结构设计
2.2.1 灵巧手主体结构设计
在满足抓取和细微前提下,手指数目应尽可能取最小值。而三指灵巧手则可以完成大多数的抓取任务。该三指灵巧手的结构采用一种特殊构型,即一个固定手指、两个旋转手指。旋转手指可同步转动180°,从而实现多种抓取动作。
三指灵巧手全手由3根手指及手腕构成,共具有4个自由度。手指采用本文的灵巧手手指方案,并对腱张紧机构和安装机构进行优化。
三指灵巧手结构模型如图4所示。
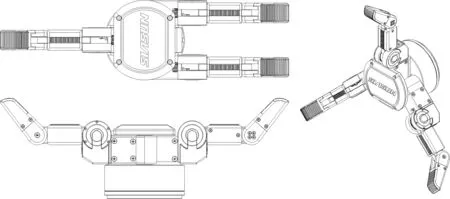
图4 三指灵巧手结构模型
2.2.2 手腕结构设计
相对于二指灵巧手,三指灵巧手增加了手腕结构,由伺服电机进行驱动。为保证两个手指转动的同步性,笔者采用了一组耦合齿轮作为同步传动机构。
三指灵巧手传动机构如图5所示。
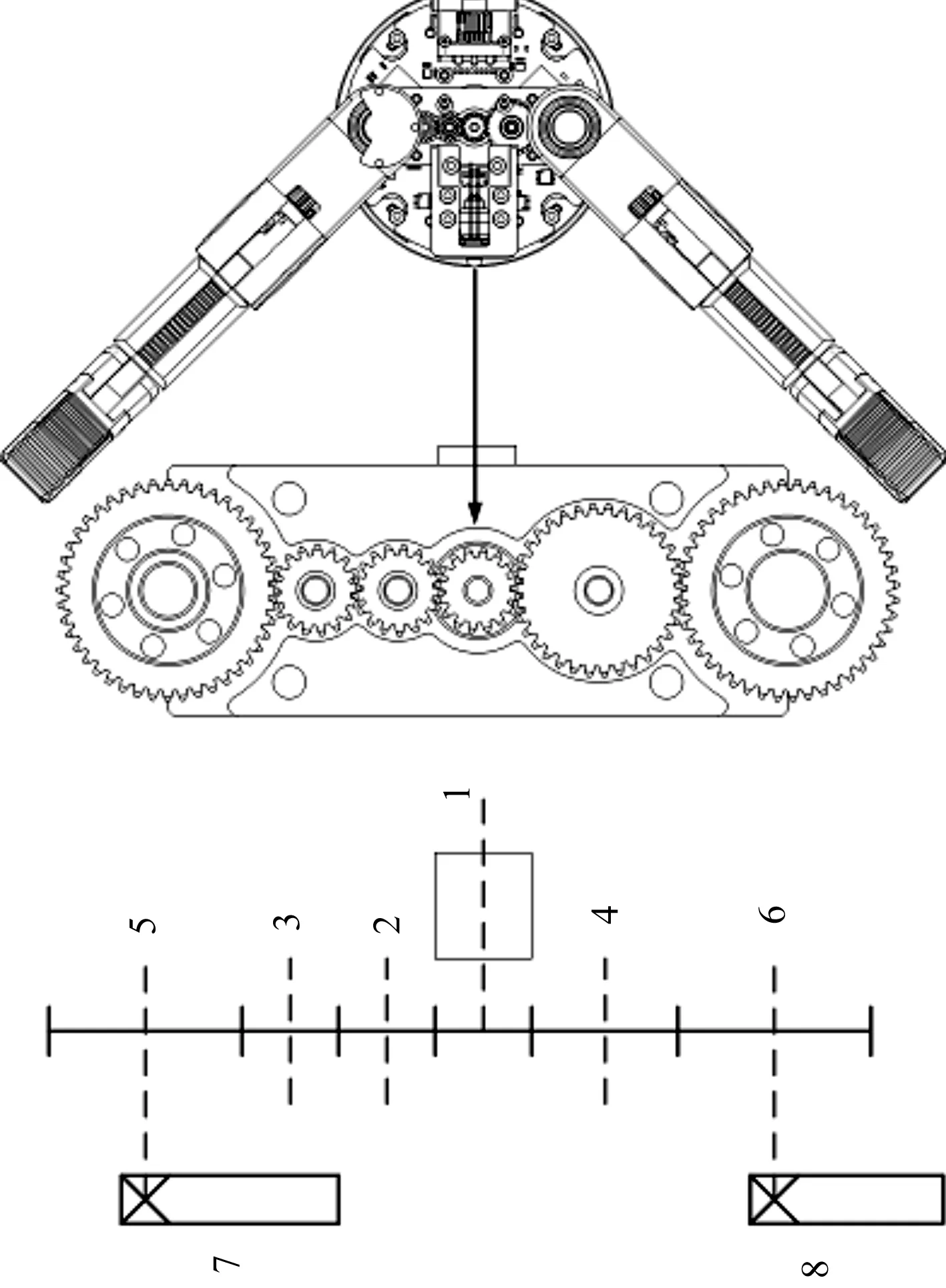
图5 三指灵巧手传动结构
图5中,当手指处于不同的运动状态及姿态时,手腕电机的负载会产生较大的变化。为了确定手腕运动的响应速度和运动精度,笔者对手腕关节的转动惯量进行计算。
各轴惯量转换至电机轴的当量转动惯量J为:
(11)
式中:Ji′(i=2,3,…,8)—第i轴对电机轴的当量转动惯量。
(12)
式中:Ji(i=2,3,…,8)—第i轴转动惯量;ωi(i=1,2,…,8)—第i轴转速。
同理,可对手指进行转动惯量计算,得到手指当量转动惯量为J′。
2.3 五指灵巧手结构设计
五指灵巧手结构与人类手部结构相似,其手指结构应具有3个关节及3段手指。除手腕结构外,五指灵巧手增加了手掌结构。
2.3.1 手指结构设计
手指整体采用模块化设计,根部关节为主动关节,其余关节通过交叉连杆机构实现耦合运动,其机构简图及手指仿生设计如图6所示。
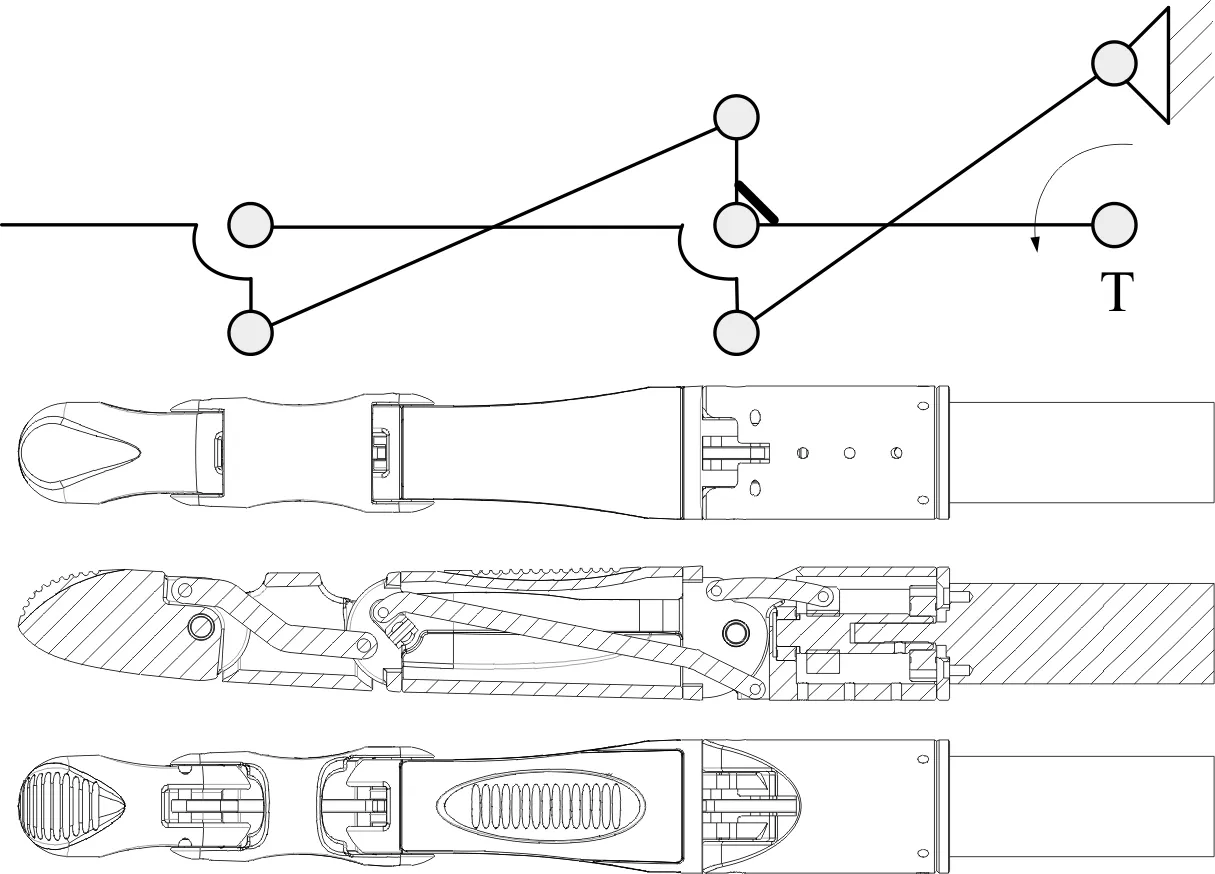
图6 手指机构简图
笔者根据图6对手指进行仿生结构设计。其中,指尖段指节长度27.3 mm,直径15.2 mm,中间段指节长度30 mm,直径17.7 mm,指根段长度50 mm,直径19.6 mm;指根部关节通过无刷电机带动梯形丝杠旋转,梯形丝杠螺母带动传动连杆运动,传动连杆为手指运动提供输入扭矩T;根据手指各部位几何关系,笔者建立手指各关节及指节长度的数学模型,对手指进行运动分析。
根据建立的数学模型,笔者得到手指弯曲过程中,指尖速度、电机驱动力随时间变化规律,如图7所示。

图7 指尖速度及电机驱动力随时间变化曲线
2.3.2 拇指及五指灵巧手结构设计
拇指结构采用一级交叉连杆机构,实现末端指节的运动耦合;旋转关节采用蜗轮蜗杆的传动方式,拇指指尖段指节长度39.6 mm,直径24.6 mm,指根段指节长度48.5 mm,直径29.6 mm,拇指可抬起最大角度52.6°。
五指灵巧手具有6个自由度,采用伺服电机驱动,手指采用模块化设计,通过交叉连杆机构实现运动耦合,如图8所示。

图8 拇指及五指灵巧手结构模型
根据五指灵巧手结构的几何关系,各手指关节运动范围如表1所示。

表1 各手指关节运动范围
3 多指灵巧手传感器设计
笔者在指尖安放触觉传感器,并在手指内部安置力矩传感器,以此来判断多指灵巧手的夹持状态;同时,在指根关节处布置绝对位置传感器,以实现精确位置控制。
根据所设计的多指灵巧手结构,笔者设计了与其配合使用的高灵敏度、低成本一维双向力传感器及触觉传感器。
3.1 一维双向力传感器
基于应变原理,笔者以本文设计的张紧机构的悬臂梁为弹性体,采用半桥贴片的方法,通过应变的变化,间接测量指尖输出力矩。
桥电路输出电压e为:
(13)
式中:ε—应变;E—供电电压;K—应变系数。
由于是间接测力机构,需首先对机构进行受力分析。
传感器结构的几何关系如图9所示。
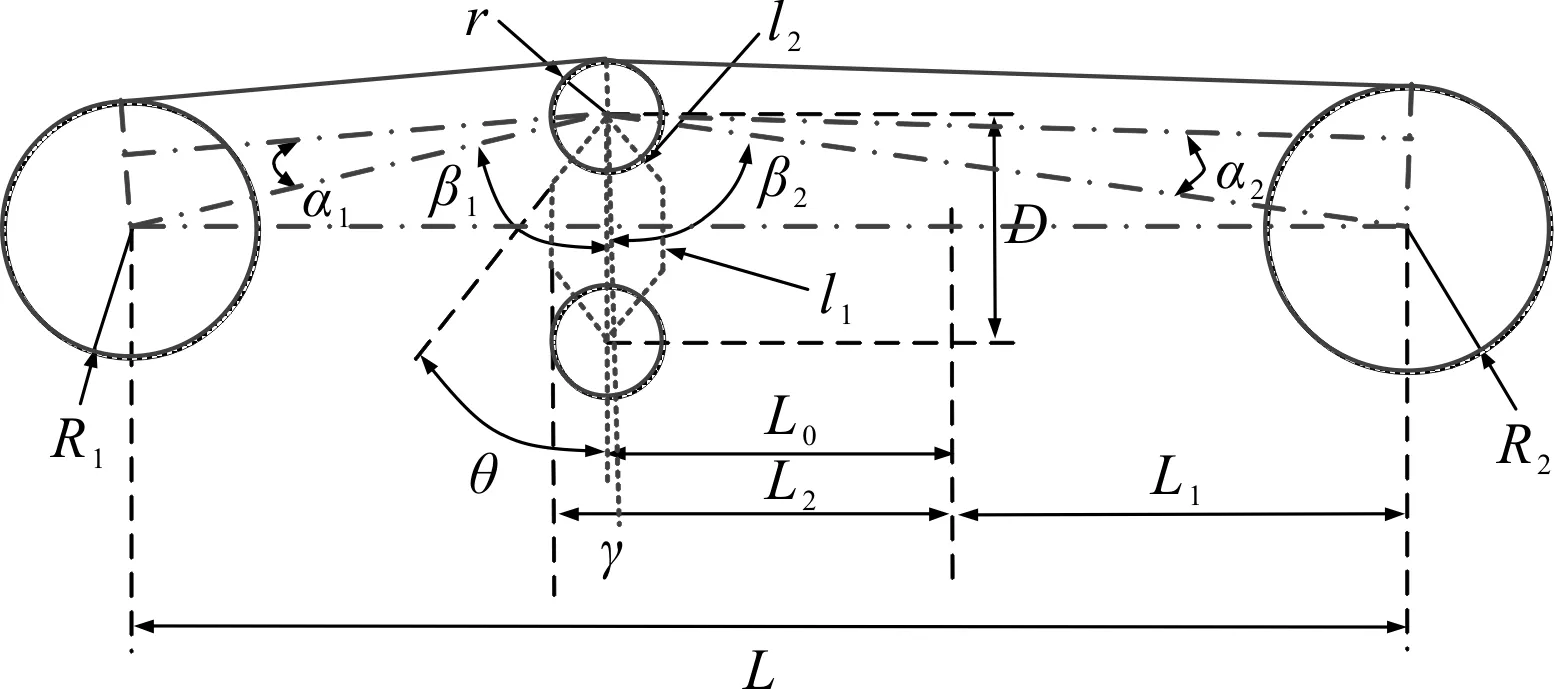
图9 传感器结构的几何关系
当末端指节受力时钢丝绳拉力增加,钢丝绳按压张紧机构,弹性体发生变形产生应变。
笔者根据几何关系,对相关参数进行计算:
(14)
(15)
(16)
(17)
(18)
D=11+2×12cosθ
(19)
(20)
式(14~20)中,各变量为具有几何意义的变量,均在图9中进行标注。
指尖受载时钢丝绳上的拉力变化ΔF为:
(21)
式中:T—钢丝绳扭矩。
紧边钢丝绳拉力F1及松边钢丝拉力F2分别为:
F1=F0+ΔF
(22)
式中:F0—钢丝绳预紧力。
F2=F0-ΔF
(23)
作用在传感器上的合力∑F为:
(24)
传感器应变ε为:
(25)
传感器输出信号e与指尖扭矩T和张紧宽度D的关系为:
e=ρTD
(26)
式中:ρ—力矩传感器常数;T—指尖扭矩;D—张紧宽度。
根据设计参数,当∑F=12 N时,应变ε为:
ε=1.9×10-3
(27)
笔者对弹性体进行有限元分析,验证计算的准确性。弹性体应变云图如图10所示。

图10 弹性体应变云图
由此可知,在测量处应变约为1.65×10-3,仿真结果与理论计算结果虽然存在一定的偏差,但误差较小,在可接受范围内。因此,可以说明传感器的理论设计是正确的。
3.2 触觉传感器结构设计
触觉传感器由弹性元件和金属箔应变片组成,弹性体结构上包含3个弹性臂,如图11所示。

图11 触觉传感器弹性体结构设计
笔者在应力集中处贴应变片,对其进行结构仿真。当指尖抓取目标物体时,3个应变片会采集弹性臂相应的应变数值。如果被抓物体发生滑移,3个应变片采集到的数据会产生不规则变化,则此时能够判断物体未抓牢,通过调整抓取力的大小,即可完成抓取任务。
触觉传感器通过力矩变化来判断物体是否滑移,对于能够产生力矩变化的物体,有两种情况发生:(1)被抓物体位姿变化引起的力矩变化,此时目标物体未发生滑移。在这种情况发生下,目标物体因为受力点的位置不变,力发生了改变。假设物体之前受力为F,变化后的力为F1,变化角度为β,则F1=F(β),3个应变片的变化规律具有一致性;(2)被抓物体发生滑移引起的力矩变化,这种情况下,应变片信号呈现出不一致性。
笔者在指尖相同位置分别加载力20 N、30 N、40 N、50 N,模拟目标物体未发生滑移情况,对弹性体进行应变仿真分析。
未产生滑移时弹性体应变云图如图12所示。

图12 未产生滑移时弹性体应变云图
通过仿真结果可知,其对应最大应变分别为:2.648 e-004,3.972e-004,5.296e-004,6.620e-004。分析其结果可知:
(28)
由仿真结果和以上计算即可验证情况(1)。当应变片采集到的信号表现出非一致性时,此时可以判断目标物体产生了滑移。
在之间不同位置施加25 N载荷,模拟目标物体产生滑移的情况,进行应变仿真分析。
产生滑移时弹性体应变云图如图13所示。

图13 产生滑移时弹性体应变云图
由仿真结果可知,发生滑移状态时,各应变片信号呈现非规律性变化。因此,在抓取操作时,当出现该情况,说明物体未抓牢,需要增加抓取力。
4 实验及结果分析
4.1 腱传动稳定性实验
多指灵巧手腱传动稳定性主要体现在其承载能力上,其稳定性主要由卡扣与钢丝绳的结合强度、钢丝绳端锁紧强度决定。工作时,腱传动机构承受单向的间歇负载或者长时间静载。
因此,笔者对腱传动机构分别在静载和间歇负载两种情况下进行测试。卡扣通过永久变形的方式与钢丝绳结合,钢丝末端完全锁死。实验时,分别对5台腱传动机构样机进行加载,锁紧绳头处用记号笔标记,记为初始位置,对末端加载2.5 kg负载,保持静置17 h,17 h后卸载,记录绳头移动量。重新加载,反复进行20组实验。
其中,前8组绳头移动量实验数据如表2所示。
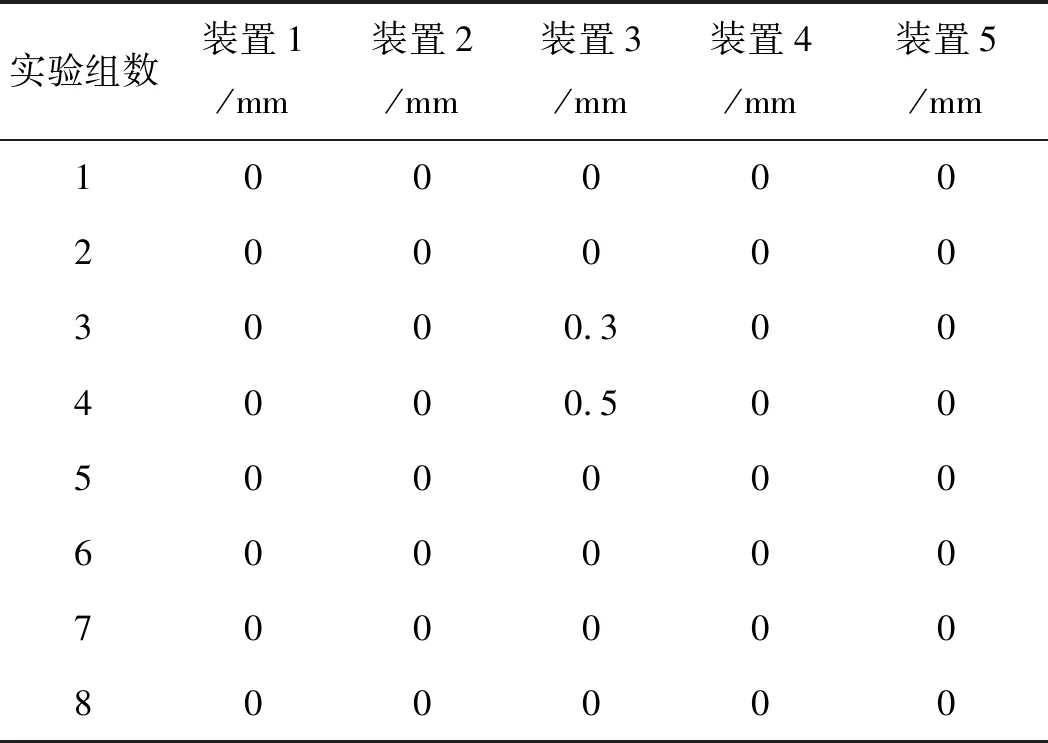
表2 绳头移动量
由表2可知,在40组实验中,只有2次实验绳头发生了移动,这是由于在反复加载过程中,操作人员操作产生振动,导致固定螺钉松动,经实验人员再次紧固并涂抹螺纹紧固胶后,这种现象再未出现。
实验结果表明,在该负载下锁紧结构是稳定、可靠、安全的。动载荷与静载荷对腱传动机构的影响是不同的,因此笔者对5台腱传动机构样机进行循环载荷实验。
动载荷变化范围为25 N~36 N,循环加载100次。前8组实验记录如表3所示。
根据表3可以发现,绳头处标记均未发生窜动,并且钢丝绳与传动轮结合处未出现断裂或者磨损。可见,该装置具有足够的稳定性及安全性。

表3 绳头移动量
通过以上实验可以证明,腱传动结构在一定的负载范围内具有较好的稳定性和可靠性。
4.2 一维力矩传感器实验
一维力矩传感器作为一个重要的测量部件,其信号与末端负载的规律性非常重要。理论上,由力矩传感器的设计可知,桥电路输出电压e与末端负载T、支撑距离有关D具有一定的相关性。当支撑距离D不变时,输出电压e与末端负载T成线性关系。
以下通过实验来验证这一规律。在支撑距离为1 mm、1.5 mm、2 mm的情况下,在输出末端依次施加1 N~30 N负载(力臂不变),间隔1 N,对相同支撑距离、相同负载情况下的输出电压重复进行实验5次,然后求得5次输出电压均值,绘制输出电压-负载曲线。
输出电压-负载曲线如图14所示。

图14 一维力传感器实验
由图14可知,在D保持不变的情况下,输出电压e与负载T基本呈线性相关。
4.3 传动效率实验
给5组机械手指分别施加0.01 N·m,0.015 N·m,0.02 N·m,0.025 N·m,0.03 N·m的输入扭矩,记录每台样机的输出扭矩,并对同一输入扭矩下测得的5组输出扭矩进行求均值操作。
实际输出效率η为:
(29)
式中:T—输出扭矩;T0—输入扭矩;i—总传动比。
实验记录如表4所示。

表4 实验记录
表4中,平均传动效率约为32.63%,与理论计算较为接近,从而验证了理论计算的正确性。
4.4 运动精度实验
灵巧手手指末端的重复定位精度,主要受末端编码器精度、响应速度、运动规划等影响。笔者设置末端编码器线数为4 096,电机编码器线数为2 048,二者的运动关系为1 ∶80,电机到末端的减速比157.7 ∶1。
电机转速和关节转速的关系如表5所示。
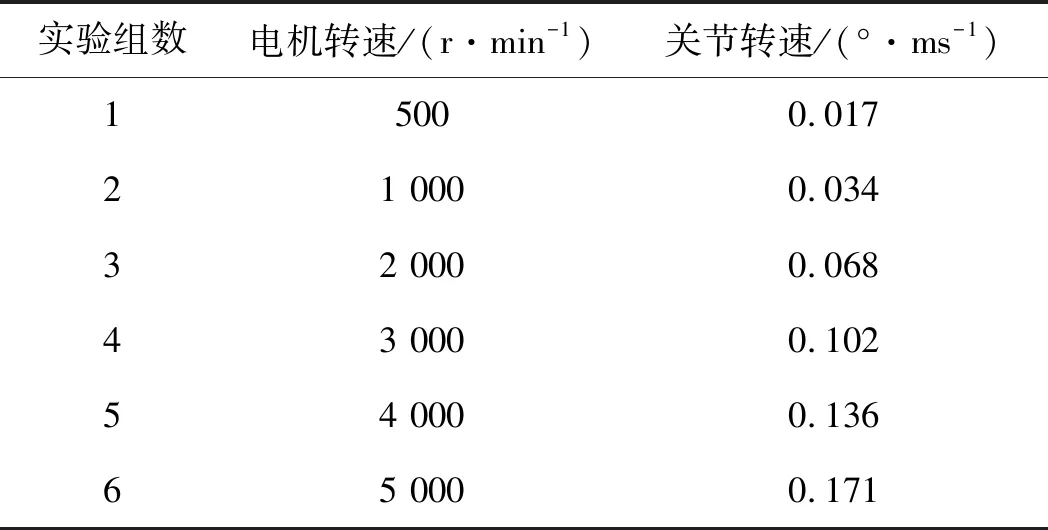
表5 电机转速与关节转速关系
在电机空载下,以表5速度开始停机到完全停止,记录关节走过的角度。
关节转角如表6所示。

表6 关节转角
通过选取数据拟合,得到关系式如下:
F(x)=-1.221 5x3×10-10+1.471 2x2× 10-6-1.601 5x×10-3+0.484 1
(30)
式中:x—电机转速。
根据以上数据,为保证夹爪有0.1°的控制精度,笔者对运动进行控制规划,控制规划曲线如图15所示。

图15 控制规划曲线 t1—加速阶段,电机以最大加速度达到设定速度所需时间;t2—定速阶段,电机以设定速度持续运动时间;t3—减速阶段,接近目标点电机以恒定加速度开始减速运动时间;t4—低速阶段,电机以最低速度向目标靠拢运动时间;t5—停止阶段,电机从收到停止指令到完全停止耗费时间;ω0—设定速度
进入低速运行阶段,电机500 r/min速度对应关节速度0.017 1 °/ms,如控制周期为5 ms,则相当于0.086 °/周期,即满足最小0.1°的精度要求,笔者对3根手指样机分别进行重复定位精度实验。
运动精度实验结果如图16所示。
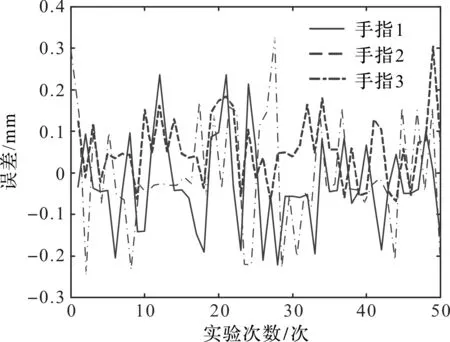
图16 运动精度实验
笔者对3组实验结果进行计算,指尖的实际平均位置偏差为-0.26 mm,等效为±0.13 mm;力臂长度为110 mm,换算成指根角度偏差为:
(31)
实验结果表明,本文采用的控制规划方法是正确的。
4.5 稳定抓取实验
为验证该三指灵巧手的稳定性,本文进行了稳定抓取实验。实验中分别对长方体、球体、不规则圆柱体等进行了稳固抓取,每种目标物体抓取10次。
稳定抓取实验如图17所示。

图17 稳定抓取实验
在30组实验中,只有2次抓取不规则圆柱体失败,这是因为不规则圆柱体物体采用空塑料瓶作为目标,自重较轻,在抓取时,灵巧手触碰目标,导致不规则圆柱体倒下,抓取失败;之后实验在不规则圆柱体中充满纯净水用以增加重量,其余抓取均成功。
实验结果表明,机械手分别以平行方式抓取长方体木块,以对心方式抓取球体,以握持和包络方式抓取不规则圆柱体,抓取稳定。
5 结束语
本文提出了一种多指灵巧手手指结构设计方案;通过设计具有不同承载能力的腱传动机构及张紧机构,实现了灵巧手手指的快速设计;提出了二指、三指及五指灵巧手的构型设计方案,实现了多灵巧手系列化设计;专用的高灵敏度、低成本一维力传感器及触觉传感器,在保证抓取效果的同时,降低了传感器成本。
相关实验结果表明,本文设计的腱传动机构具有较高的稳定性,手指结构具有较好的运动性能;传感器具有较高的灵敏度和较好的一致性,三指灵巧手可以完成不同形状物体的抓取任务。

