考虑截面形变的伸缩臂臂架动力学特性研究*

谢 瑶，张 磊*，唐亚鸣，丁根宏

(1.河海大学 机电工程学院，江苏 常州 213022；2.河海大学 理学院，江苏 南京 210098)

0 引 言

伸缩臂臂架常见于起重机、挖掘机和高空作业车等工程机械中，广泛应用于建筑、消防等行业[1，2]。在工作过程中，伸缩臂臂架截面由于外力的原因容易产生拉伸、弯曲等变形[3]，直接影响到工程设备的工作性能。对此的相关研究方面，传统的梁理论忽略了翘曲、畸变等高阶变形，难以反映臂架真实的力学行为，所以有必要深入研究伸缩臂臂架的动力学特性。

针对伸缩臂臂架的动力学分析，国内外学者进行了深入的研究。王志彪、蒙树立[4，5]将臂架模拟成柔性体模型，结合柔性多体动力学和基础振动理论，建立了臂架的刚性模型和柔性模型；都亮[6]对高空作业车模型进行了运动弹性动力学分析，并基于KED方法对臂架系统的多柔体动力学方程进行了求解；李涛等[7-9]将臂架简化为具有端部质量的变截面阶梯梁，基于梁的振动理论，结合边界条件和连接处连续性条件，建立了伸缩臂的动力学模型，李圣[10]和SAWODNY O[11]基于哈密顿原理推导了各节臂架的振动方程，求解了臂架前三阶振型函数及固有频率。但在以上的研究中，臂架的动力学模型大都是通过解析法建模，求解过程复杂，且在建立臂架模型时很少考虑截面畸变、翘曲等高阶形变对于臂架动力学的影响，使得计算结果存在一定的误差。

本文考虑包括臂架截面拉伸、扭转、畸变、翘曲等形变的完全耦合，根据广义位移和广义坐标建立截面中线上的位移场，结合哈密顿原理，分别建立臂节和伸缩臂系统的动力学模型，并通过数值算例验证其可行性；同时分析在不同几何参数条件下，高阶特征形变对伸缩臂振动性能的影响。

1 伸缩臂系统的物理模型

本文考虑两节臂架的伸缩臂系统，将伸缩臂简化为一端固定的矩形薄壁梁，认为第一节臂架的内表面和第二节臂架的外表面在连接处固定贴合。

伸缩臂结构简图如图1所示。

图1 伸缩臂结构简图

图1中，以臂架截面中心为原点建立空间坐标系(x，y，z)，两节臂架长度分别为(l1+l3)和(l2+l3)，两节臂架的厚度均为t。

2 伸缩臂系统的动力学建模

2.1 臂节的动力学模型

在考虑了截面变形对于臂节动力学建模的影响基础上，笔者在截面中线上建立局部坐标系，如图2所示。

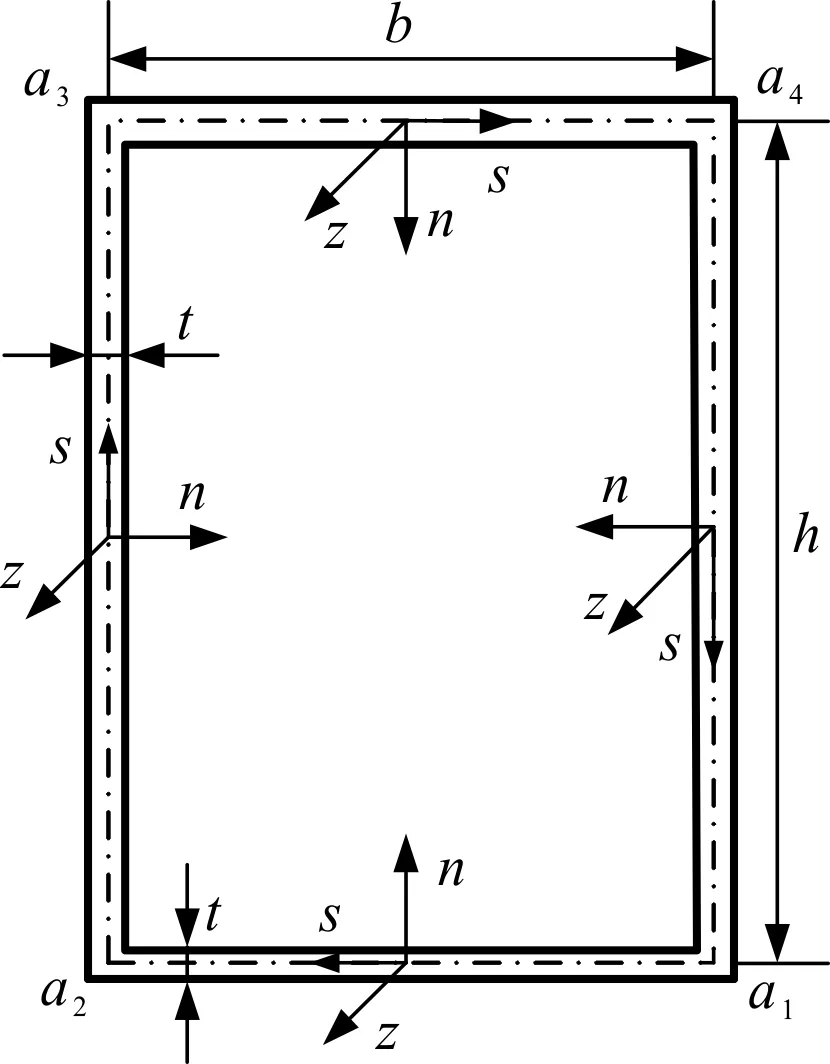
图2 截面中线上的局部坐标系

图2中，截面宽度和高度分别为b和h，局部坐标系由切向s、法向n和轴向z定义，用于描述截面在各个方向上的变形。其中，切向坐标s以a1为起点沿截面中线逆时针方向，法向n与s垂直并指向壁板内侧。

本文借鉴张磊[12]对矩形薄壁梁的分析方法，通过考虑截面8种变形模式来完成臂节的动力学建模。

变形模式如图3所示。

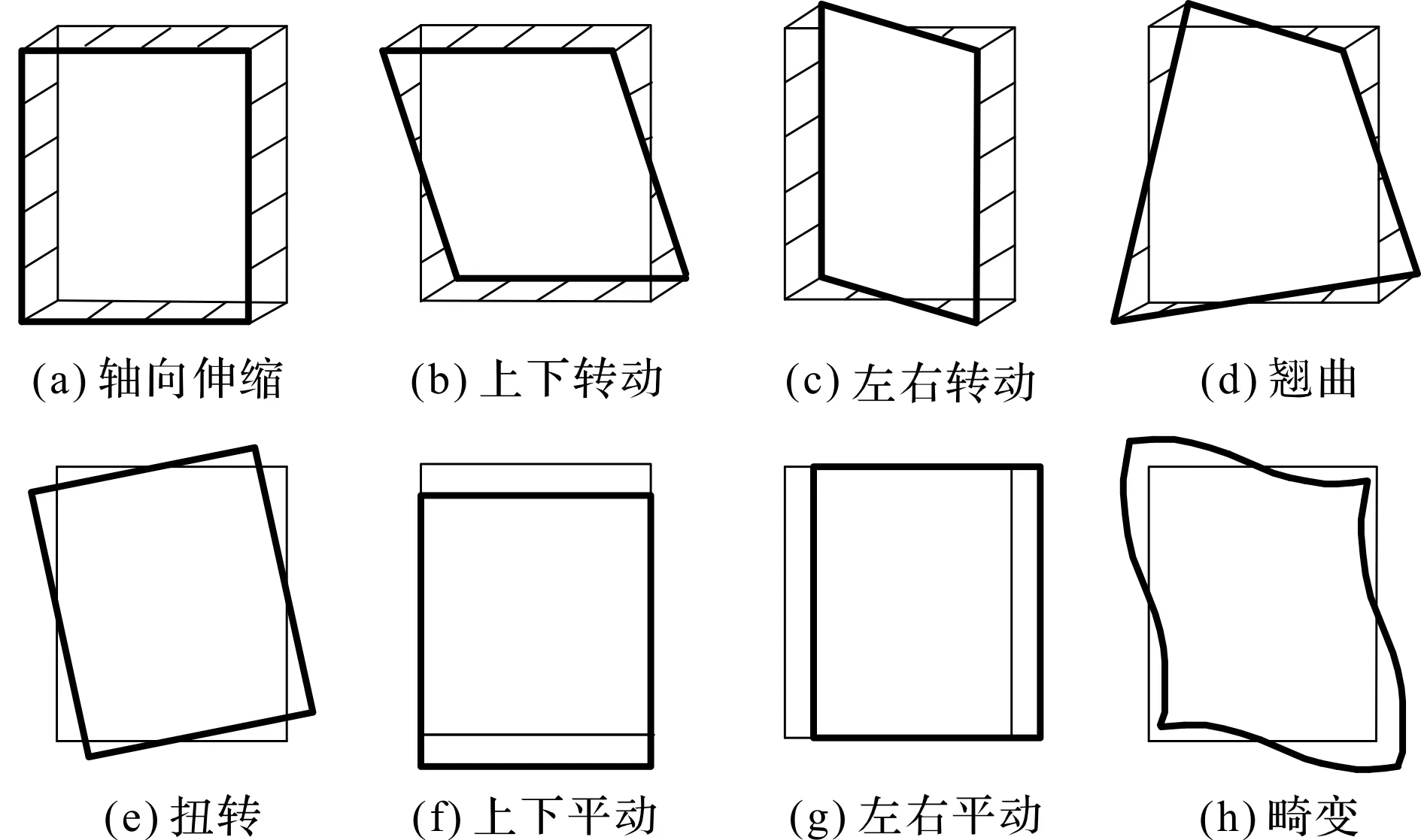
图3 变形模式

图3中，变形模式图3(a～c,e～f)是基于铁木辛柯梁理论的低阶特征形变，变形模式图3(d,h)是基于翘曲和畸变的高阶特征形变；变形模式的形函数推导方法可以直接借鉴[13]。

笔者采用模态叠加的方法，将定义在臂架轴线上的截面变形模式的形函数线性叠加，用轴向u(s,z)、切向v(s,z)和法向w(s,z)3个位移分量来表示截面中线上点的位移，即：

(1)

式中：φ(s)—平面外变形的广义坐标；ψ(s)，ω(s)—平面内变形的广义坐标；χ—广义位移向量。

χ=[χ1(z)χ2(z) …χ8(z)]T

(2)

二维位移分量b可以表示为：

b=ψχ

(3)

式中：ψ—变形模式对应的广义坐标。

(4)

三维位移场B(u,v,w)可由二维位移分量b转换而得：

B=Lb

(5)

式中：L—微分算子。

(6)

根据哈密顿原理有：

(7)

式中：T—臂架的动能；U—臂架势能；W—外力势能。

且有：

(8)

式中：ρ—臂架材料密度。

(9)

式中：ε—应变向量；σ—应力分量。

即有：

ε=CB

(10)

σ=Ehε

(11)

式中：C—微分算子；Eh—本构矩阵。

即：

(12)

(13)

式中：E—杨氏模量；v—泊松比；G—剪切模量。

W为：

(14)

式中：Λ—轴向的积分区域；Ω—s坐标的积分区域；n—薄壁梁的外表面；p，q—作用在臂架截面上的分布力列向量。

将式(8～14)代入式(7)，可得：

(15)

将式(2～6)代入式(15)，即可得到控制微分方程的具体形式。

本文采用有限单元法求解臂节的控制方程，通过拉格朗日插值函数沿轴线方向将臂节离散为n个单元，即:

χ=Ndi,i=1,2…n

(16)

式中：i—单元节点号；N—线性插值形函数；d—单元i的节点位移向量。

且有：

(17)

di=[χ1(i) …χ8(i)χ1(i+1) …χ8(i+1)]T

(18)

式中：ξ1，ξ2—形函数；(i)，(i+1)—单元两端。

则臂节总体节点位移向量Dr可以表示为：

Dr=[χ1(1) …χ8(1) …χ1(n) …χ8(n)]T

(19)

将式(16～19)代入式(15)，可得：

(20)

式中：l—单元长度。

并将控制微分方程的形式整理为：

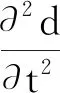
(21)

式中：m—单元质量矩阵；k—单元刚度矩阵。

(22)

(23)

笔者通过MATLAB编制相应的有限元程序，求解单元质量矩阵m和单元刚度矩阵k，结合边界条件，组装形成臂节的总体质量矩阵M1和总体刚度矩阵K1，其中：

(24)

(25)

式中：Tri—节点位移向量di到总体节点位移向量Dr的转换矩阵。

2.2 臂架连接处动力学模型

笔者分别用两节臂架的位移场来表示连接处的位移，理论上前一节臂架内表面与后一节臂架外表面在连接处位移应该相等，但考虑到模型简化，两种位移场表示的位移存在一定的差值，借鉴JANG等[14]在研究薄壁梁的处理方法，认为在位移场差值最小条件下的计算精度最高。

用两节臂架的位移场表示连接处的位移，即：

Br1=Lr1ψr1Ndr1

(26)

Br2=Lr2ψr2Ndr2

(27)

两节臂架在连接处的位移场差值可以表示为：

(28)

将式(26，27)代入式(28)，当差值取极值点时最小，即：

(29)

式中：T—dr1与dr2之间的转换矩阵。

考虑到(Lr1ψr1N)T不恒为0，即有：

Lr1ψr1Ndr1-Lr2ψr2NTdr1=0

(30)

转换矩阵T可以表示为：

T=(T2)-1T1

(31)

式中：T1，T2—转换矩阵。

T1，T2分别为：

(32)

(33)

2.3 伸缩臂系统的动力学建模

参考臂节的建模方法对第2节臂架进行动力学建模，考虑臂架连接处的位移连续性，完成伸缩臂系统的动力学建模。

两节臂架的运动方程分别为：

(34)

(35)

式中：D1，D2—对应臂架节点位移向量。

将两节臂架的节点位移向量分别用伸缩臂整体节点位移向量D表示，则有：

D1=TaD

(36)

D2=TbD

(37)

式中：Ta，Tb—转换矩阵。

依据臂节模型离散方法，将两节臂架依次离散为n1和n2个单元，且连接处为n3个单元，则伸缩臂共有(n1+n2-n3)个单元，且不考虑固定端的位移向量，则共有(n1+n2-n3)个独立节点，则有：

Ta=[I8n1×8n108n1×8(n2-n3)]

(38)

(39)

n=8n3-16n2+32

(40)

将伸缩臂系统的整体运动方程表示为：

(41)

则有：

M=(Ta)TM1Ta+(Tb)TM2Tb

(42)

K=(Ta)TK1Ta+(Tb)TK2Tb

(43)

式中：M—质量矩阵；K—刚度矩阵。

3 数值算例与动力学特性分析

利用MATLAB求解质量矩阵和刚度矩阵的广义特征值，即可转化得到系统的固有频率。因此，笔者通过比较本文模型与ANSYS模型计算结果的差异，分析在不同尺寸、不同边界条件下，高阶形变对于臂架动力学特性的影响。

3.1 算例1：臂节模型

臂节模型取伸缩臂结构的左端一节。参数包括：长度l1=0.55 m，l3=0.05 m，臂节截面b1=0.065 m，高度h1=0.086 m，厚度t=0.005 m，密度ρ=7 850 kg/m3，弹性模量E=2×1011Pa，泊松比v=0.3。

考虑到臂节模型的收敛性，此处的一维高阶模型将臂节离散为60个单元；ANSYS模型采用shell181单元，控制单元尺寸为10 mm，将模型离散为1 920个Shell 181单元，其中沿臂架轴向60个单元。

臂节模型前10阶固有频率的比较如表1所示。

表1 臂节前10阶固有频率的比较

表1数据表明，此处的一维高阶模型与ANSYS模型计算结果吻合良好，误差在1%以内，验证了臂节动力学模型的准确性。

与传统的铁木辛柯梁理论模型相比，本文高阶模型的优点在于考虑了截面翘曲和畸变的影响。

笔者对不同几何参数的臂节模型进行数值分析，分析高阶特征形变对于臂节动力学特性的影响。

不同长度的臂节模型前6阶固有频率对比如表2所示。

表2 不同长度的臂节模型固有频率对比

表2中，在不同臂节长度下，本文模型的计算结果与ANSYS结果吻合良好；且对比数据发现，臂节模型的固有频率随着梁体长度的增加而减小。

不同厚度臂节前6阶固有频率对比如表3所示。

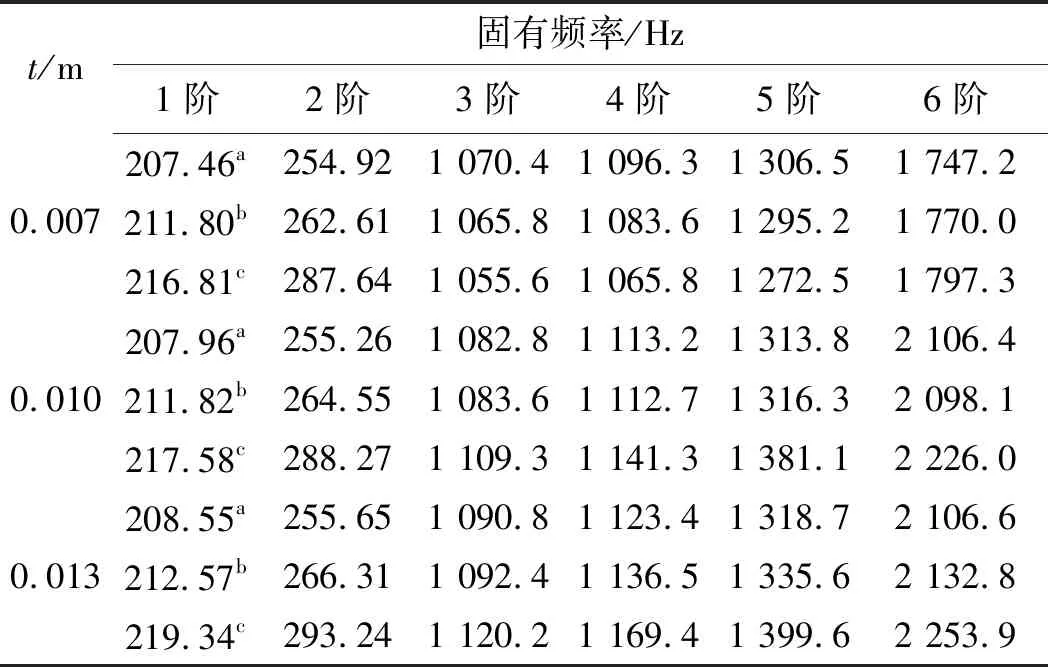
表3 不同厚度的臂节模型固有频率对比

表3中，在不同臂节厚度下，本文模型的计算结果与ANSYS结果吻合良好；且臂节模型的固有频率随着臂架厚度的增加而增加。

综合以上数据表明：(1)本文的一维高阶模型适用于不同几何尺寸臂架的求解；对于长度越长、厚度越小的臂架，一维高阶模型和铁木辛柯梁模型的计算结果相差越小，表明此时高阶特征形变对于臂架振动的影响越小；(2)两者的计算结果在前2阶时差别不大，表明此时高阶特征形变的影响可以忽略，但随着模态阶数的增大，两者误差呈增大趋势，此时高阶特征形变的影响不能忽略，否则误差最高可达10%的。

与ANSYS相比，本文方法将臂节离散为较少的单元，有着更高的计算效率，对不同几何参数的臂架，只要修改对应模型参数即可，无需重新建模。

不同边界条件下，ANSYS模型、本文模型和Timoshenko梁模型的前20阶固有频率对比如图4所示。

由图4可知，在不同边界条件下，一维高阶模型与ANSYS模型结果都吻合良好；但在两端固定条件下，一维高阶模型与铁木辛柯梁模型二者的差值明显，表明两端固定约束下，高阶特征形变对于臂架振动的参与度更高。

图4 不同边界条件下固有频率对比图

3.2 算例2：伸缩臂模型

伸缩臂的结构如图1所示，其长度l2=0.75 m，截面宽b2=0.055 m，高度h2=0.076 m，其他参数同上。

一维高阶模型将伸缩臂沿轴线方向离散为135个单元；两节臂架在连接处可认为处于固定约束，ANSYS模型通过耦合所有方向自由度来模拟两节臂架的接触情况，单元尺寸为10 mm，共离散为3 880个Shell 181单元，其中沿臂架轴向为135个单元。

伸缩臂前10阶固有频率的对比如表4所示。

表4 伸缩臂前10阶固有频率的比较

表4数据表明：一维高阶模型与ANSYS模型计算出的伸缩臂固有频率结果吻合良好，误差在1.2%以内，由此验证了伸缩臂模型的可靠性。

不同连接处长度的伸缩臂模型前6阶固有频率对比如表5所示。

表5 不同连接处长度(l2)的伸缩臂固有频率

表5数据表明：随着长度l2的增加，伸缩臂整体长度减小，固有频率总体上呈缓慢增大趋势，与臂节模型的变化规律吻合。

4 结束语

针对伸缩臂臂架动力学建模繁琐、求解复杂和精度不高的问题，笔者提出了一种考虑截面变形模式的伸缩臂臂架动力学建模及其求解方法，并且得到了如下的研究结论：

(1)与ANSYS相比，本文方法有着更高的计算效率，对于不同几何参数的臂架，只要修改对应模型参数即可，无需重新建模；

(2)本文对于臂节模型和伸缩臂系统建立的动力学模型与ANSYS计算结果吻合良好，证明该方法是可靠的；

(3)对于伸缩臂系统前2阶模态，高阶特征形变可以忽略；高于2阶模态，一维高阶模型和铁木辛柯梁模型的计算结果出入较大，此时必须考虑翘曲和畸变高阶特征形变的影响，且随着模态阶数的增大，高阶特征形变对臂架振动的参与度越高；

(4)臂架的固有频率随着梁体厚度的增加而增加，随长度的增加而减小，随高度的增加而减小。