高空作业平台臂架水平直线运动中的振动分析*
邓 铭,纪爱敏,张 磊,王 豪,赵仲航
(河海大学 机电工程学院,江苏 常州 213022)
0 引 言
高空作业平台是一种将人员、材料和设备等举升到所需位置,并进行作业的大型机械装备[1]。而随着实际工况的不断变化,单一的伸缩、变幅和回转已经无法满足施工中反应快速和操作便捷等需求,因此,需对作业平台的运动轨迹进行规划[2,3]。也就是要根据实际作业任务的要求,计算出预期运动轨迹,并在工作平台沿轨迹运行过程中,对其添加速度、位移以及加速度等约束。
水平直线运动就是轨迹规划中一种,通过对臂架伸缩运动与变幅运动进行相互约束,使臂架顶部工作平台沿水平直线运动。实际施工时不仅要使工作平台能准确沿直线运动,而且还要研究其运动的振动特性,使其平稳运行以保证乘员舒适与安全[4]。
曹旭阳[5]、陈添明[6]等人对高空作业平台直线轨迹与运动空间进行了论述分析,建立了数学模型,结合控制过程中动力元件环节和阀组特性,得出了在臂架运动过程中的理论运动曲线与实际振荡曲线;同时,也有部分学者不考虑动力元件等影响因素,从动力学角度分别对高空作业平台臂架在变幅运动与伸缩运动中的振动特性进行了研究工作。
PERTSCH A等[7]在分析变幅运动臂架动态响应时,保持臂长不变,变幅角变化,将全伸状态下的臂架系统等效为带有端部集中参数的变截面悬臂梁,后建立了动力学方程,利用模态叠加与传递矩阵求出了臂架端部的动态响应;在臂架伸缩运动方面,王亮、WANG L H等[8,9]用Galerkin方法,分析了带有集中参数的轴向运动变长度悬臂梁的振动特性,以及对其进行的控制;杜文正[10]将伸缩臂架拆分成独立的臂节,并考虑支撑底座的激励作用和振动微分方程,求解了臂端的振动响应。
以上对臂架振动特性研究,都是单纯针对臂架的变幅运动与伸缩运动,但却并没有考虑两者的复合运动。
本文由臂架顶部做水平运动的几何关系约束反推出臂架伸缩与变幅运动相互限制关系,将臂架等效为底部铰接,叠加部位具有弹性支承、集中参数的变截面、变长度梁;利用Hamilton原理得出振动微分方程,以及其在不同时间下的瞬态振型参数,后拟合近似表示出不同臂长的实际振型,回代入振动微分方程,在Matlab/Simulink中进行动态仿真,得出臂架头部的振动响应。其中,本文所述水平直线运动是复合运动的其中一种。
1 轨迹计算公式
高空作业平台主要由下车、转台、变幅机构、伸缩机构、调平机构、臂架以及作业平台组成,这些部分相互协调配合来完成各项工作。
高空作业平台水平直线运动过程如图1所示。

图1 高空作业平台水平直线运动示意图
在作业平台沿水平直线运动过程中,笔者根据高空作业平台逆运算结构简图,通过几何运算,将工作平台运行轨迹逆运算至高空作业车俯仰机构和伸缩机构,得到变幅角度以及伸缩长度的运动轨迹。
水平直线运动的抽象图如图2所示。
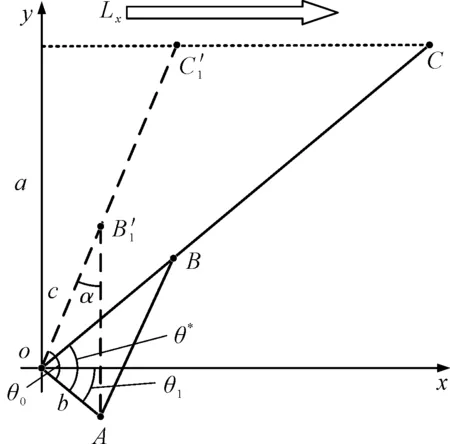
图2 水平直线运动抽象简图
从几何关系可以看出,在高空作业平台做水平直线运动过程中,臂长发生变化,平台水平高度保持不变,即:
l(t)sin(θ*(t)-θ1)=a
(1)
(2)
式中:l(t)—臂架长度;L0—臂架初始长度;θ0—初始变幅角度;θ1—液压缸铰接角度;a—臂架运动高度;Lx—水平位移距离;θ*—变幅角度;α—变幅缸与臂架夹角;c—臂架铰接点O与变幅缸铰接点B长度;b—臂架铰接点O与变幅缸铰接点A长度。
两边对时间求导得:
(3)
式中:v—臂架水平匀速运动时最大速度,并规定水平伸出为正,水平缩回为负。
对上式求解微分方程得:
(4)
(5)
(6)
2 振动模型建立
在分析臂架振动特性时,此处将作业平台和工作人员视为集中质量与转动惯量,同时考虑其横向变形的影响,将各臂节视为Euler-Bernoulli梁。
2.1 变幅缸等效刚度
在建模时,笔者考虑臂架根部与变幅液压缸之间距离,将变幅缸等效为一连接臂架与转台的弹性支承。
目前应用广泛的双作用单出杆液压缸如图3所示。
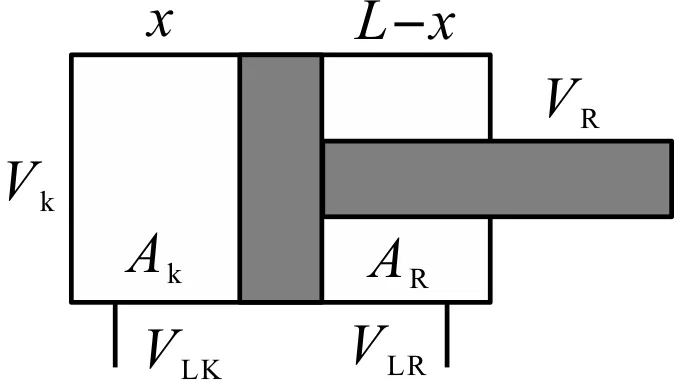
图3 双作用液压缸工作简图
参考文献[11],可知液压弹簧刚度为:
(7)
式中:βe—液压油体积模量;A—容器的工作面积;V—密封容器的液压油容积。
双作用变幅液压缸工作时,左右两侧的液压弹簧为并联,故总的液压油刚度为两侧油刚度,即为:
(8)
式中:x—液压缸活塞位移距离;L—行程;AK,AR—液压缸左右两侧工作面积;VK,VR—液压缸左右两侧容积;VLK,VLR—液压缸两侧管道内油液死容积。
2.2 臂节间叠加处理
臂架作同步伸缩运动时,臂架之间的叠加距离较长,且会随着时间变化,故在进行振动分析时,不能直接忽略。因此,笔者在忽略臂节与臂节的搭接间隙的基础上,将叠加部分视为材料属性与力学属性叠加的新臂节。
具体的臂节分段如图4所示。

图4 臂节分段变化示意图
本文研究的直臂式高空作业平台拥有3节臂的臂架,令其拥有6段臂节,但在臂架不停的伸缩运动中,臂架的搭接情况会发生变化,6节臂节会交替出现。
定义任一臂节b的属性为:
(9)
式中:z—臂节b上任意一点在z轴上的距离;m,mm—组成臂节b的起始与末尾臂架;ρAi,EIi,vi,Pi(z)—臂架每节臂的线密密度、抗弯密度、速度和轴向力;ρAb,EIb,vb,Pb(z)—臂节b的线密度、抗弯密度、速度和轴向力。
2.3 臂架横向振动模型
此处以臂架与转台的铰接点为坐标原点o建立坐标轴,其中以未变形臂架的中轴线为z轴,以垂直于臂架的中轴线的方向为ω轴;以过o点平行于地面为x轴,垂直于地面为y轴。
高空作业平台臂架抽象结构模型如图5所示。

图5 具有分布参数的臂架抽象模型 θ—臂架的变幅角度;ω(z,t)—臂架的中性轴挠度;α—变幅缸与臂架的夹角;K—液压等效刚度;mc,Jc—臂架顶部的集中质量和转动惯量
根据Hamilton原理有:

(10)
式中:T—臂架的动能;V—臂架势能;W—作用于臂架系统的保守力虚功。
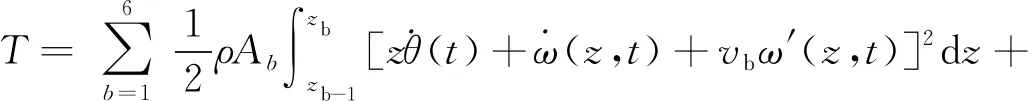
(11)

(12)
δW=Mδθ(t)+Fδxz(t)
(13)
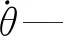
将式(11~13)代入式(10)中,得到臂架变幅运动的动力学偏微分方程;结合臂架底部铰接处边界条件,可得臂架两端边界条件臂节之间几何与力学连续性条件,具体如下式所示:
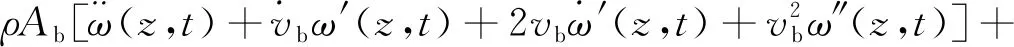
(14)
ω(0,t)=0
(15)
ω″(0,t)=0
(16)
(17)

(18)
(19)
(20)
(21)
(22)
式中:ωb(z,t),δ(z-a)函数—臂架上某点到水平线的弧度和狄克雷函数;狄克雷函数—在z=a变幅缸处等效支承刚度。
3 臂架动力学求解
3.1 水平直线运动中的横向振动特性求解
在臂头做水平直线运动的过程中,臂架的变幅角度与伸缩长度都会发生变化,随着臂长的不断变化,每段臂节的频率与振型函数都会不断地发生变化,故无法根据式(14)直接求解臂头的时变动态响应。
参考文献[12]中计算方法,为求解瞬态振动特性,将运动过程在时间域内进行离散,只考虑单一时刻的静态函数,省去与速度相关项,后在时间域内利用多项式拟合出与臂长相关函数,近似替代求解动力学方程。
同时,由于梁等连续体振动的动力学特性,如频率与振型式仅与动力学偏微分方程以及边界条件的齐次部分有关,故动力学方程式、边界条件式(17,18)和连续性条件式可分别化为:
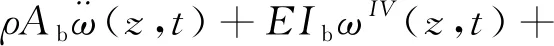
(23)
(24)
(25)
(26)
笔者运用模态叠加法进行近似求解,即假设在任一时刻,横向振动ωb(z,t)可以由该时刻对应无数阶固有振型函数φ(z)与广义坐标q(t)的乘积和表示,即:
(27)
式中:下标i—第i阶固有振型函数。
(28)
(29)
式中:w(l)—梁长为l时的固有频率;γb(l)—臂长为l时的频率特征值。
将式(27)代入式(23),结合式(28,29),则臂段b的频率特征值为:
(30)
对式(30)进行拉氏变换与反变换:

(31)
其中:kb=Kα/EIb;Sb、Tb、Ub、Vb参考文献[13];H(z)=H(z+zb-1-a)H(a-zb-1)H(zb-a)。
根据传递函数法,将臂架的边界条件(15,16,24,25),臂节的连续条件(19~21,26)、代入振型函数系数式(31),可得齐次方程组式:
(32)
式中:B,C,D参考文献[14];Pb—臂节b振型。
(33)
在伸缩过程中,臂节组合与长度发生变化,各臂节频率特征值γN(l)不断变化。将式中频率特征值代入式中,使得齐次方程组的系数矩阵仅含一个未知量l,可得臂架在伸缩过程中的任意长度l、阶数i、臂节b的频率特征值γb,i(l),代入式(31,32),可得臂节b的任意阶振型基函数φb,i(z,l);

最后,通过模态叠加法就可得出臂架近似振型函数。
3.2 水平直线运动中的横向振动响应求解
根据Galerkin法,笔者假设在任一时刻横向振动ωb(z,t)可由该时刻所对应臂架的固有振型函数线性叠加,即:
(34)
将式代入动力学微分方程,结合边界条件(15~18)与连续性条件(19~22),经化简可得:
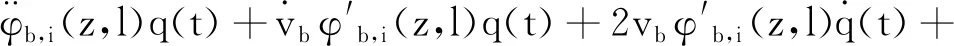
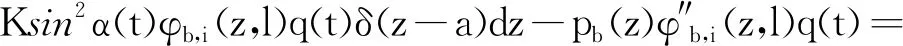
(35)
将上式两侧同乘以φb,j(z,l),并在[0,l]上积分,可得t时刻臂架系统的质量矩阵M、阻尼矩阵C、刚度矩阵K和载荷向量F:
(36)
(37)
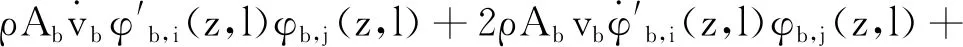

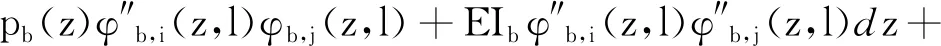
Kαφb,i(z,l)φb,j(z,l)h(zb-1,z,zb)+
(38)
(39)
在模态叠加中,三阶以后影响较小,考虑计算的效率与结果的准确性,故此处采用Galerkin截断法选取前两阶模态进行计算,即:
(40)


(41)
(42)
(43)
(44)

4 具体算例
此处以某一24 m三节直臂伸缩式高空作业车为例,分析其在水平直线运动中臂架头部的动态响应。
其液压系统参数如表1所示。

表1 液压系统参数
臂架具体参数如表2所示。
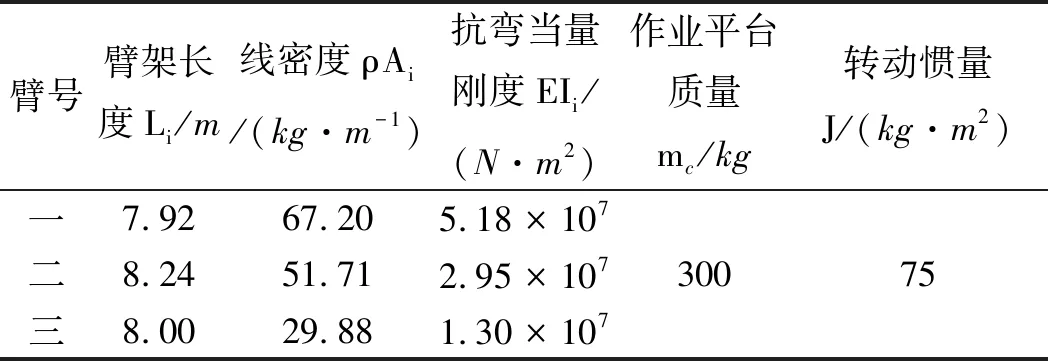
表2 臂架参数
当作业平台水平向右运动时,设定臂架初始长度为11.77 m,初始角度为60°,工作高度为10.2 m,臂架的变幅角度为34.82°,长度为17.67 m。
运动过程中,臂架伸缩长度与变幅角度变化图如图6所示。

图6 臂架伸缩长度与变幅角度变化图
图6中,变幅角度不断减小伸缩长度不断增加;同时,随着臂架伸缩长度的不断变化,臂段的长度与组合产生变化。
各臂段具体长度如图7所示。
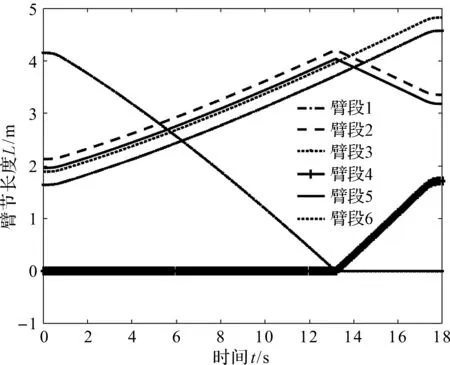
图7 各臂节长度变化图
在臂架伸缩过程中,笔者选取随时间变化的臂长点l,根据式(31,32)计算所得频率特征值与振型函数系数,分别使用多项式对其进行拟合。
其中,频率特征值拟合曲线如图8所示。
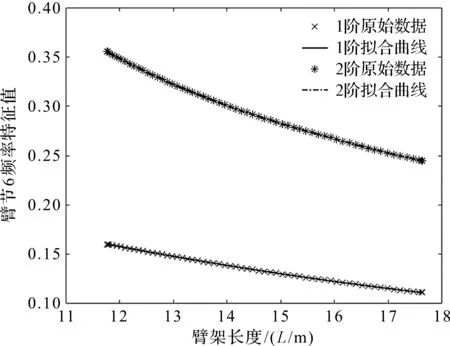
图8 频率特征值拟合曲线
考虑准确性与计算效率,此处笔者采用三阶多项式拟合频率特征值。前两阶频率特征值γ6(l)随臂长l的增加不断减小。振型函数系数γ6(z5,l)、γ6′(z5,l)、γ6″(z5,l)、γ6‴(z5,l),采用五阶多项式进行拟合。其中,一阶振型函数大于二阶振型;且随着长度增加,振型函数系数也在不断增加,但增长速度变慢。
臂架一阶具体的振型函数拟合曲线如图9所示。
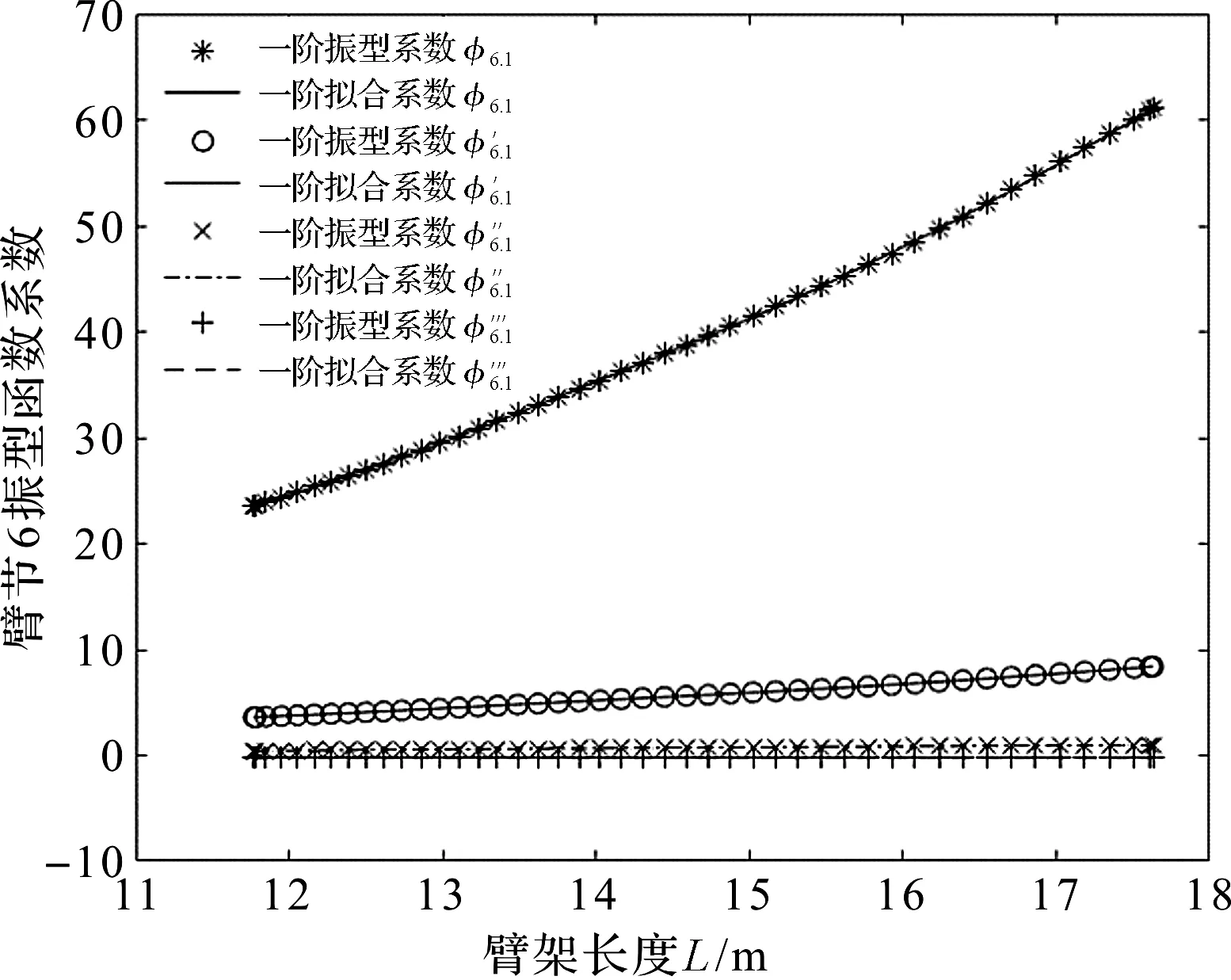
图9 一阶振型函数系数拟合曲线
臂架二阶具体的振型函数拟合曲线如图10所示。
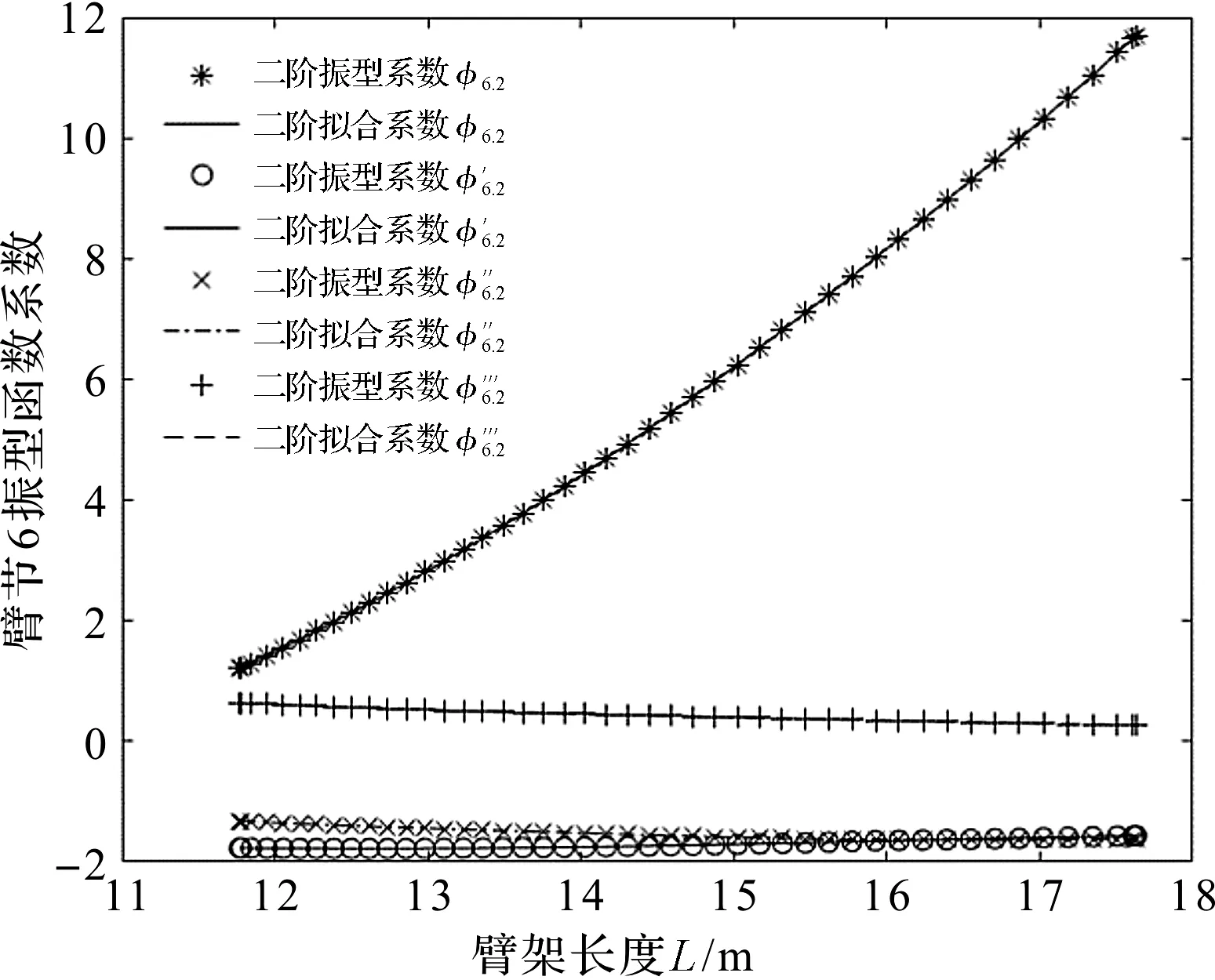
图10 二阶振型函数系数拟合曲线
在式(38)求解t时刻载荷向量系数时,笔者将水平直线运动过程中的变幅角度θ(t)用三次多项式进行拟合,可得出关于臂长l的函数;求解出在t时刻对应臂长为l的动力学方程矩阵系数(35~37),代入式(40),可得出状态空间方程;在Matlab/Simulink环境下进行仿真模拟,可得出臂头动态响应。
其中,随着臂架水平直线运动距离Lx的增加,臂架头部振动频率降低,振幅变大,并在17 s左右达到最大幅值。
臂架水平直线运动中臂架头部的振动位移响应如图11所示。
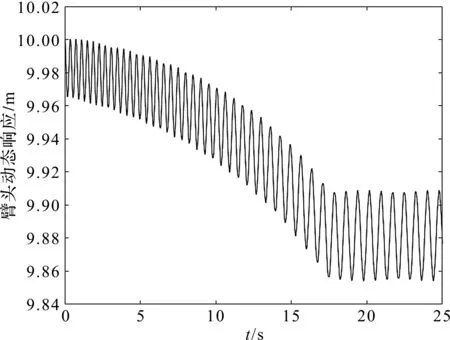
图11 臂头部振动响应曲线
5 结束语
针对高空作业平台直线轨迹运动中的振动问题,笔者分析了平台沿水平直线运动时,臂架伸缩运动与变幅运动相互关系。
考虑臂架实际搭接与实际支承情况,笔者将臂架等效为底部铰接且具有弹性支承,叠加部位为具有集中参数的变截面、变长度梁;基于Hamilton原理建立了臂架在运动过程中的动力学方程,结合模态叠加法,在时域上离散,求解了在不同长度下的瞬态振型函数;通过拟合近似等效臂架实际振型,然后利用Galerkin截断法得出了广义坐标下的状态空间方程,在Matlab/Simulink环境下得出了臂架在水平直线运动过程中头部的振动响应。
该研究工作可为高空作业平台臂架在直线轨迹运动中的振动控制提供理论参考。

