基于ISFLA优化深度置信网络的滚动轴承故障诊断方法研究*

齐洪方，黄定洪

(1.武汉华夏理工学院 智能制造学院，湖北 武汉 430223；2.武汉理工大学 机电工程学院， 湖北 武汉 430070)

0 引 言

滚动轴承作为旋转机械设备的关键零部件，其健康状态直接影响设备整体运行的安全性和可靠性。有数据统计显示，由于轴承发生故障导致机械设备不能正常运行的比例约为30%[1]。因此，研究一种高效、稳定、可靠的轴承故障诊断方法尤为重要。传统的故障诊断方法大多采用傅里叶变换[2]、小波变换[3]、经验模态分解[4]等信号处理技术[5,6]，对故障振动信号进行人为特征提取和特征选择，然后输入到分类器中进行故障分类，依赖于一定的信号处理技术和专家经验。

深度置信网络(DBN)作为经典的深度学习算法之一，具有强大的自适应特征提取能力和非线性数据处理能力，可直接对原始时域振动信号进行数据处理[7]，因而被广泛应用于飞机发动机[8]、滚动轴承[9]、齿轮[10]等的故障诊断中。

由于结构参数选择是否合理对DBN特征提取起着至关重要的作用，在当前的研究中，对于DBN模型各隐含层神经元个数以及反向微调学习率的选择，大多是根据经验人为进行的选择。混合蛙跳算法(SFLA)是一种基于群体协同搜索启发式算法，其结合了模因算法和粒子群优化算法(particle swarm optimization，PSO)的优点[11]，具有全局搜索能力强、收敛速度快、易跳出局部极值点等优点。

基于以上原因，本文提出一种基于改进的SFLA优化DBN故障诊断模型，并将其应用于滚动轴承的故障诊断中。

1 深度置信网络

在结构上，DBN是由多个受限玻尔兹曼机(restricted boltzmann machine，RBM)堆叠而成的多隐含层神经网络模型。

DBN模型结构如图1所示。

图1 DBN模型结构 v—输入层；h1—第一隐含层；h2—第一隐含层；h3—第三隐含层；output—输出层即Soft-max分类器；v—可视层神经元；h—隐含层神经元

DBN的结构参数主要包括：输入层神经元个数、输出层神经元个数、反向微调算法学习率、算法迭代次数，以及RBM1、RBM2和RBM3隐含层神经元个数。

DBN训练的过程分为两个阶段：(1)由低层到高层的RBM无监督逐层预训练过程；(2)由高层到低层的反向微调学习过程。

2 基于ISFLA优化DBN的轴承故障诊断模型

2.1 ISFLA算法及参数选择

针对SFLA算法在实际应用中存在早熟收敛的现象，ZHANG等人[12]将PSO算法中“个体认知”能力应用到SFLA中，从而达到改善SFLA认知行为的目的。

改进后的混合蛙跳算法(ISFLA)更新规则如下式所示：

s=r1(Ub-Uw)+r2(Ug-Uw)

(1)

式中：r1，r2—[0,1]之间的随机数；Uw—局部最差蛙；Ub—局部最优蛙；Ug—全局最优蛙。

跳跃步长的计算如下式所示：

(2)

式中：S—跳跃步长。

更新后的青蛙可表达为：

(3)

ISFLA是一种基于种群的启发式算法，因此，初始种群的好坏对算法的搜索性能极其重要。当初始种群在可行域中分布不均匀时，将导致算法的搜索范围受到一定的限制，从而降低算法的全局搜索能力。因此，本文采用正交设计来初始化青蛙种群[13]。

根据文献[14]中给出的参考范围，ISFLA参数选取如表1所示。

表1 ISFLA参数列表

为了保证青蛙族群的多样性，防止陷入局部最优，笔者在随机选择q只青蛙构建子族群Msub时，对适应度值较大的青蛙赋予较大的权重，适应度值较小的青蛙赋予较小的权重。

权重比例分配如下式所示：

(4)

式中：n—青蛙族群个数；pj—第j只青蛙的权重比列。

2.2 ISFLA-DBN轴承故障诊断模型

笔者利用ISFLA对DBN各隐含层神经元个数和Adam优化算法学习率进行参数寻优，以提高模型的故障诊断性能。

基于ISFLA优化DBN的轴承故障诊断模型如图2所示。

该模型主要分为3个步骤：振动故障信号采集、故障特征提取和故障识别。

具体过程为：

(1)振动故障信号采集。利用加速度传感器对故障设备进行振动信号采集，并按照一定的采样步长进行样本采样。为消除变量之间的量纲和数量级的影响，对样本进行数据预处理，然后将样本按照一定的比列划分为训练集、验证集和测试集；

(2)故障特征提取。首先，将训练集和验证集数据输入到经ISFLA优化的DBN模型中进行训练，使得各隐含层间的连接权重和偏置达到最优状态，提高DBN从原始时域信号中的自适应特征提取能力，从而达到降低训练损失误差和提高训练精度的目的；然后，将测试集数据输入到模型中进行故障特征提取；

(3)故障识别。将DBN最后一个隐含层提取到的特征向量输入到Soft-max分类器中进行故障分类，并将分类结果与期望输出(标签数据)进行比较，得到故障识别精度，并将结果进行可视化处理。

3 实验验证

3.1 数据来源及样本划分

为验证模型的有效性，本文采用美国凯斯西储大学轴承数据集[15]进行实验验证。

实验台如图3所示。

图3 轴承实验台

图3中，主要包括一个驱动电机、一个负载电机、加速度传感器和扭矩传感器。其中，加速度传感器固定在驱动电机轴承上方的电机外壳上，采样频率为12 kHz。

笔者选取转速为1 797 r/min、负荷为1 hp和转速为1 772 r/min、负荷为2 ph两种工况，对包括轴承内圈轻微故障、轴承内圈中度故障、轴承内圈严重故障、轴承外圈轻微故障、轴承外圈中度故障、轴承外圈严重故障、滚动体轻微故障、滚动体中度故障、滚动体严重故障，以及正常轴承状态共10种故障类型的数据分别进行实验研究；

取400个采样点为一个样本长度，每种工况取150个样本，则每种故障类型共有300个样本，10种故障共3 000个样本，按照3 ∶1 ∶1的比例划分为训练集S、验证集V和测试集T。

3.2 实验对比模型构建

该实验主要分为3个层次：(1)选取未优化的DBN模型与ISFLA-DBN模型进行对比；(2)选取以BP为代表的浅层网络与ISFLA-DBN模型进行对比；(3)选PSO-DBN与ISFLA-DBN模型进行对比。

具体如下：

(1)ISFLA-BP模型

利用ISFLA对三层BP神经网络进行参数优化，由输入样本数据的维数以及滚动轴承故障类别可知：BP神经网络输入层和输出层神经元个数分别为400和10；利用ISFLA对BP神经网络中隐含层神经元个数n和学习率η进行参数优化，得到的BP神经网络结构为：400-164-10，学习率为0.038 425 5。

(2)DBN模型

采用逐级递减的方式[16]来确定DBN的结构参数，即后一层神经元个数小于前一层神经元个数；由输入样本数据的维数、滚动轴承故障类别，以及逐级递减方式，可以确定DBN模型结构为：400-300-200-100-10，Adam算法学习率为0.001。

(3)PSO-DBN模型

利用PSO算法[17]对DBN模型中各隐含层神经元个数，以及Adam算法学习率进行参数寻优，得到DBN的模型结构为：400-812-558-422-10，Adam优化算法学习率为3.698e-4。

(4)ISFLA-DBN模型

利用ISFLA对DBN模型各隐含层神经元个数，以及Adam优化算法学习率进行参数寻优，得到DBN的模型结构为：400-956-628-384-10，Adam算法学习率为8.634e-4。

3.3 结果分析与讨论

3.3.1 DBN与ISFLA-DBN对比分析

在训练集和验证集上，DBN和ISFLA-DBN模型的准确率变化曲线如图4所示。

图4 准确率变化曲线图

由图4可知：在验证集上，ISFLA-DBN模型的准确率、拟合效果以及算法趋于稳定时所需的迭代次数均优于DBN模型。

损失误差变化曲线如图5所示。

图5 损失误差变化曲线图

由图5可知：在验证集上，ISFLA-DBN模型的损失误差要远低于DBN模型，即采用ISFLA对DBN结构参数进行优化，可有效提高模型的故障诊断性能。

3.3.2 ISFLA-DBN逐层特征提取能力

由于滚动轴承样本数据集和ISFLA-DBN模型中每一隐含层提取到的特征维数较高，不利于可视化观察。为了便于进一步评估ISFLA-DBN模型特征提取能力，笔者对样本数据集和ISFLA-DBN模型中各隐含层的输出数据，利用t分布随机近邻嵌入流形学习算法，进行降维可视化操作。

原始数据可视化特征图如图6所示。

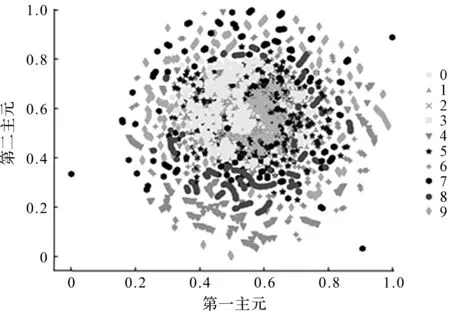
图6 原始数据可视化特征图

由图6可知：10种故障信号的特征相互交错，无法进行故障分类。

第一隐含层可视化特征图如图7所示。

图7 第一隐含层可视化特征图

由图7可明显看出：经第一隐含层RBM1特征提取之后，10种故障信号由最初混乱无序的状态开始有效地聚集到一起。

第二隐含层可视化特征图如图8所示。

图8 第二隐含层可视化特征图

由图8可知：经过第二隐含层RBM2特征提取之后，10种故障信号基本上全部剥离开来。

第三隐含层可视化特征图如图9所示。

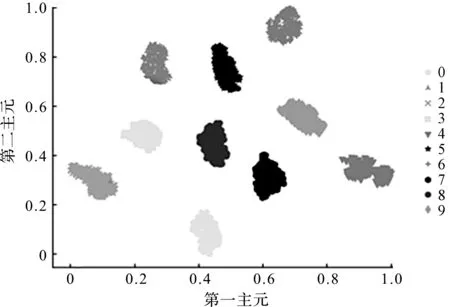
图9 第三隐含层可视化特征图

由图9可知：经过第三隐含层RBM3特征提取之后，除了极少部分的数据出现重叠现象之外，在整体上已经达到了很好的特征提取效果。

综上可知，ISFLA-DBN模型能够有效地对原始时域振动信号集进行故障特征提取，避免了传统故障诊断方法人为特征提取的弊端，使得诊断过程更加智能化。

3.3.3 ISFLA-BP、DBN、PSO-DBN和ISFLA-DBN对比分析

4种模型在训练集上的故障分类准确率变化曲线的对比如图10所示。

图10 准确率变化曲线图

由图10可知：ISFLA-DBN、PSO-DBN和DBN3种模型在训练集上的故障分类准确率都能达到99%以上；其中，ISFLA-DBN的收敛速度最快，算法趋于稳定时所需的迭代次数最少；ISFLA-BP模型在训练集上的故障分类准确率最高只有92%左右，且算法趋于稳定时需要迭代250次左右。

损失误差变化曲线如图11所示。

图11 损失误差变化曲线图

由图11可知：ISFLA-DBN在训练集上的损失误差最小，PSO-DBN的损失误差次之，ISFLA-BP的损失误差最大。

在验证集上，4种模型故障分类准确率和训练时间的10次运行结果平均值如表2所示。

表2 10次运行结果

由表2可知：

(1)ISFLA-DBN在验证集上的故障分类准确率平均值最高(98.57%)，略高于PSO-DBN(97.32%)，高于DBN(93.19%)和ISFLA-BP(82.93%)；

(2)由于ISFLA-DBN网络结构最为复杂，其训练时间要远大于DBN和ISFLA-BP，略高于PSO-DBN。

3.3.4 ISFLA-DBN模型泛化性能分析

为进一步评估ISFLA-DBN模型的泛化性能，即检验模型在未知数据集上的故障分类准准确率，笔者将测试集数据T输入到经训练集和验证集数据训练好的ISFLA-DBN模型中，分别进行故障分类，并将测试集诊断结果以混淆矩阵表示，如图12所示。

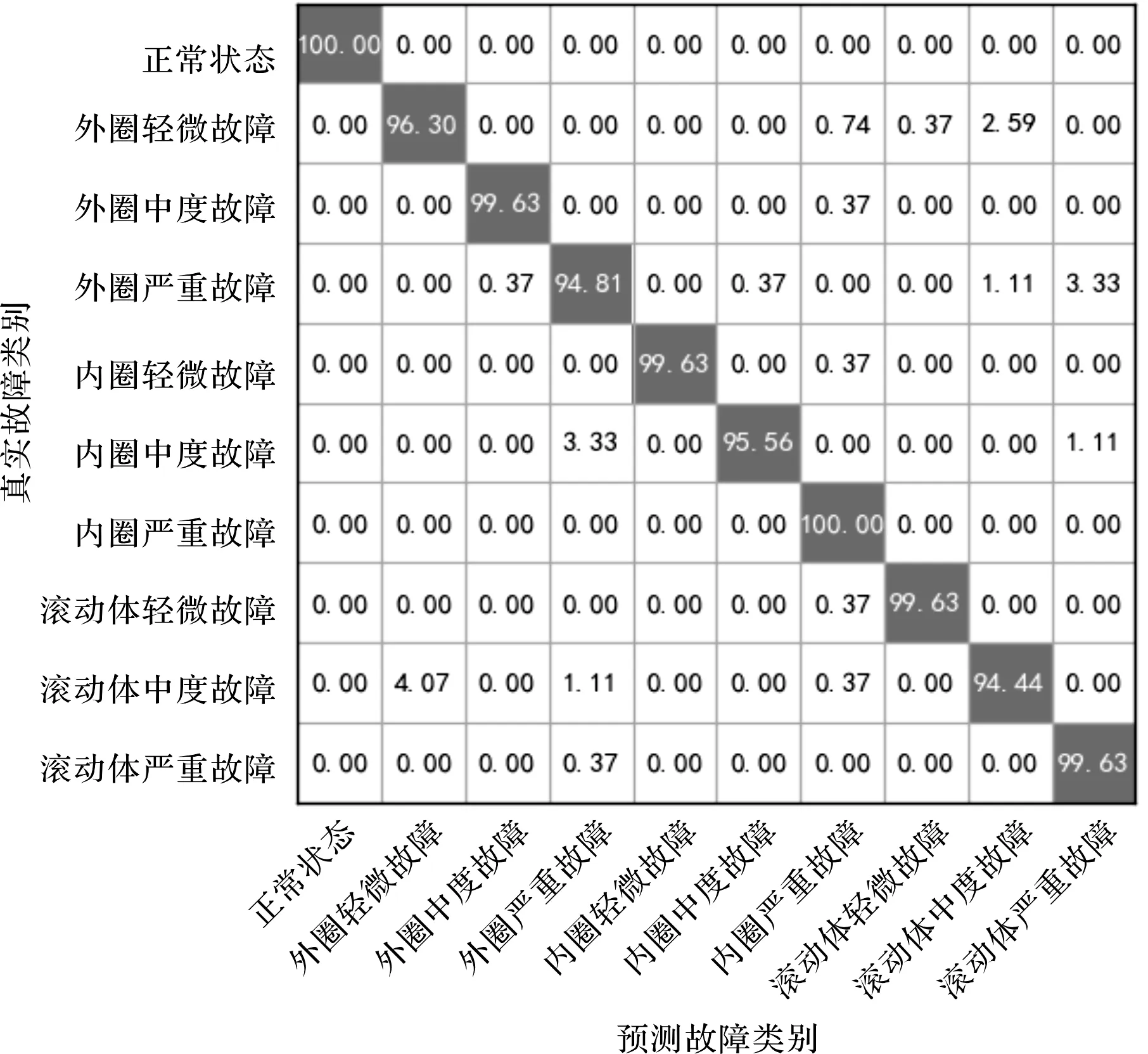
图12 测试集故障分类混淆矩阵图

由图12可知：ISFLA-DBN模型在测试集上的平均准确率为97.96%。

其中，正常轴承和内圈严重故障识别准确率达到100%，外圈中度故障、内圈轻微故障、滚动体轻微故障以及滚动体严重故障识别准确率达到99%以上，外圈轻微故障和内圈中度故障识别率分别为96.30%和95.56%，外圈严重故障和滚动体中度故障识别率较低，分别为94.81%和94.44%。

由此可见，ISFLA-DBN模型在未知数据集上的泛化性能较好，具有一定的工程应用价值。

4 结束语

本文针对传统故障诊断方法依赖于一定的专家经验和信号处理技术，以及DBN参数选择困难等问题，提出了一种基于ISFLA优化DBN的故障诊断方法，笔者采用该方法，并利用ISFLA全局搜索能力强、收敛速度快、易跳出局部极值等优点，对DBN结构参数进行了寻优。

实验及研究结果表明：

(1)相对于浅层BP神经网络故障识别精度的平均值，ISFLA-DBN模型故障识别精度的平均值高出15.64%，相对于未优化DBN模型故障识别精度的平均值高出5.38%，相对于PSO-DBN模型故障识别精度的平均值高出1.25%；

(2)ISFLA-DBN模型的收敛速度最快、拟合效果最好，在未知数据集上具有很好的泛化性能。