基于改进AMD的岸边集装箱起重机大车轨道顶部高低差计算方法研究*

陈晴岚，胡 雄，王 冰

(上海海事大学 物流工程学院，上海 201306)

0 引 言

岸边集装箱起重机(岸桥)是在港口完成大型集装箱装卸的大型起重设备，该设备具有结构复杂、服役时间长的特点。在工作环境的影响下，码头会出现不均匀沉降，导致大车轨道顶部高低差发生变化。大车轨道顶部高低差能够表征大车轨道的健康状态。根据《GB/T10183-2018》，当该参数超过标准规定的±10 mm公差范围，将会造成车轮踏面与轨道表面接触不实，引发“啃轨”现象，给岸桥带来严重的安全隐患[1,2]。测量该参数的传统方法是定期进行水平度测量，但该方法容易耗费大量的人力物力，且受工况影响，实时性差，不能真正消除安全隐患。对大车轨道顶部高低差进行实时监测和分析，对于提升岸桥的安全可靠性，具有重要的应用价值。

上海海事大学提出的状态监测方案[3]目前得到了一系列应用。该方案监测岸桥前大梁与水平面间的角度振动信号,运用小波包分解方法提取信号中的超低频信号成分，即信号的超低频趋势项，以此刻画由大车轨道顶部高低差引起的角度变化，进而得到大车轨道顶部高低差的状态。研究表明，该问题中待提取的超低频趋势项通常为信号中0.001 Hz以下的极低频率成分，因此需要进行多层的小波包分解才能提取出该部分信号成分，而且小波包分解不具备自适应性[4]。

在时频分析方法中，作为一种具有自适应性的方法，经验模态分解(EMD)法[5]在趋势项提取方面得到了广泛应用。但EMD的工作原理导致其在对大数据量的信号进行分解的过程中将消耗大量时间，影响计算效率。而近年来提出的解析模态分解(AMD)法,只需构造一对具有相同特定频率的时变正交函数，便可利用希尔伯特变换，将某一具有特定频率成分的信号分解出来，其本质相当于一个自适应的低通滤波器，在计算效率方面具有一定的优势，并且其在信号分离和趋势项提取方面得到了成功应用[6，7]。不过AMD法的处理结果会受到信号中随机噪声的影响。

鉴于上述情况，笔者提出一种基于改进AMD法的大车轨道顶部高低差计算方法，并分别采用仿真信号和实测信号验证该方法的有效性。

1 解析模态分解及其改进

1.1 解析模态分解

解析模态分解(AMD)是CHEN和WANG[8]于2012年提出的一种信号分解方法，能够将频率密集的信号分解成多个单分量信号，其基本原理和计算方法如下：

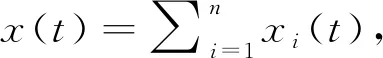
(1)

式中：si(t)—频率小于ωbi的信号分量，si(t)=sin(ωbit)H(x(t)cos(ωbit))-cos(ωbit)H(x(t)sin(ωbit))(i=1,2,…,n-1)，其中：H(·)—希尔伯特变换。

由上述原理可知，AMD可以对任意频率成分的信号进行提取。若规定信号中频率小于指定频率fc的信号成分为信号的趋势项，那么令ωbi=2πfc，根据式(1)求出的信号成分则为信号的趋势项。

1.2 解析模态分解改进

从AMD的原理可以看出，在运用AMD对信号进行分解时，信号中的随机噪声也会参与三角正交基以及希尔伯特变换的运算，使得分解结果中包含随机起伏。

滑动平均算法是消除数据中随机起伏的经典算法，算法简便、计算量小，只需对数据值进行递推计算，即可消除动态测试数据中的随机起伏，非常适合从函数形式未知或难以选用某种多项式来拟合的复杂测试数据中，快速获得其中的确定性成分[9]。

笔者关注的由岸桥大车轨道顶部高低差引起的角度变化，便属于难以用函数形式表达的情况。因此，笔者将滑动平均算法与原始AMD法相结合，改进原始的AMD法，对由AMD法提取的趋势信号进行处理，消除趋势信号中的随机起伏。

改进后的方法步骤如下：首先，令ωb1=2πfc，运用AMD根据式(1)求出信号中频率小于指定频率fc的信号成分x1(t)作为信号的趋势项；然后，对x1(t)作滑动平均，即可得到消除随机起伏后的趋势信号。

在上述步骤中，笔者采用的滑动平均算法具体如下：

假设数据长度为N的待处理信号yn由有效信号xn和随机起伏en构成，即yn=xn+en，取滑动平均的窗口长度为k，对yn进行滑动平均，提取xn。

(1)当k为奇数时，数据yn(i)为滑动窗口中心，则有：

(2)

(2)当k为偶数时，数据yn(i-1)和yn(i)为滑动窗口中心，则有：

(3)

上述算法中，滑动平均的窗口长度k直接影响数据的平滑效果：(1)k值过大，虽然可以很好地抑制信号中的随机起伏，但信号中原本的趋势信息也会一起被平均而削弱，使得处理结果与实际的趋势项产生较大偏离；(2)k值过小，虽然能保证处理结果完整保留原有信号的变化趋势，但却不能有效抑制随机起伏。

为此，笔者通过实验的方式选取最优的k值。首先，取不同的k值分别对由AMD提取的趋势项进行处理；然后，在确保随机起伏得到有效抑制的基础上，选择使处理结果与实际趋势项间偏离最小的值，作为最优的滑动平均窗口长度。

2 基于改进AMD法的大车轨道顶部高低差计算方法

为了准确计算岸桥大车轨道顶部高低差，笔者提出了一种基于改进AMD法的计算方法，在从前大梁平放状态下的角度振动信号中提取超低频趋势项的过程中，采用改进AMD法。

基于改进AMD法的岸桥大车轨道顶部高低差计算流程如图1所示。

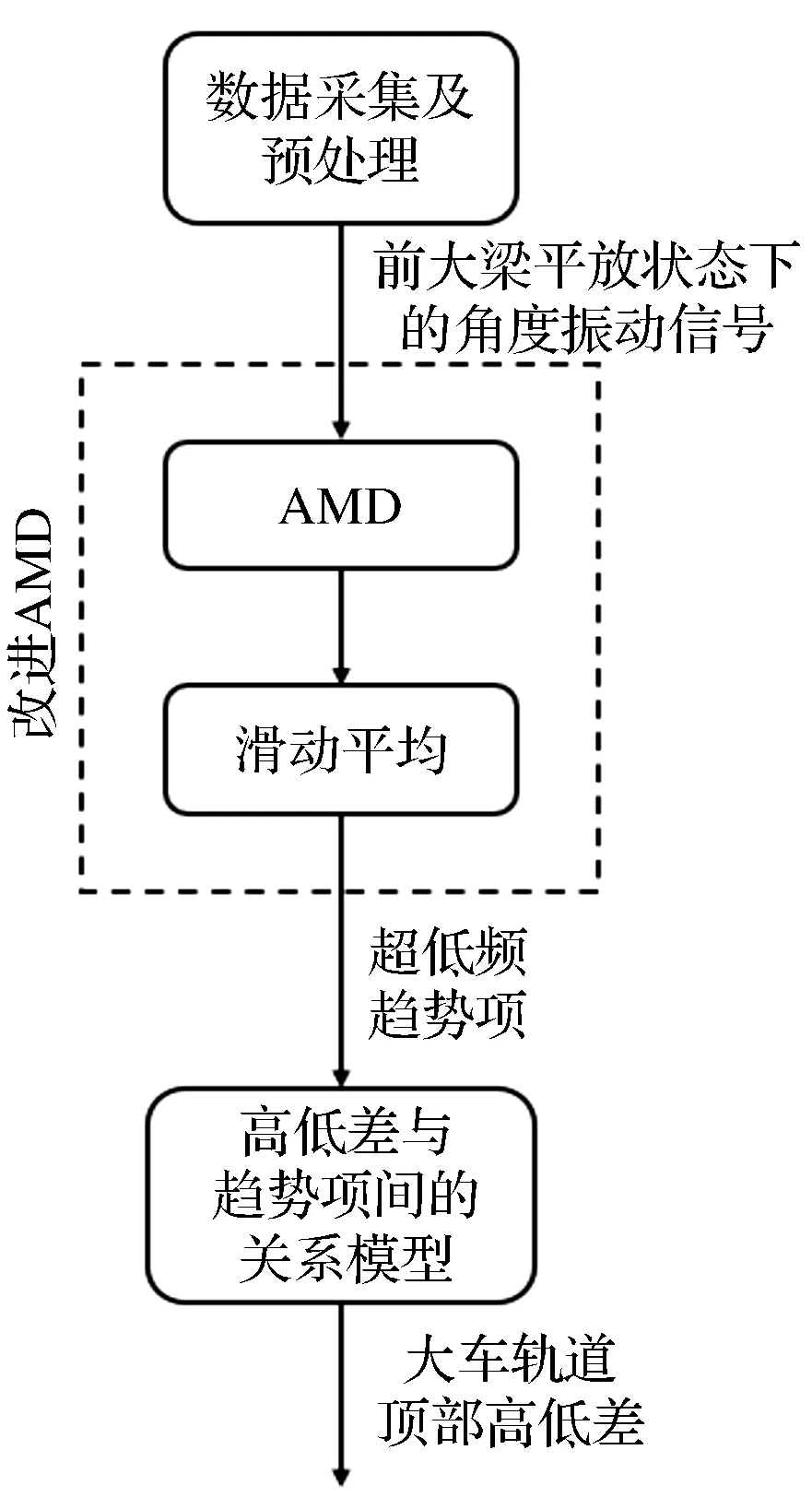
图1 基于改进AMD法的岸桥大车轨道顶部高低差计算流程

方法的具体操作步骤为：

(1)数据采集及预处理。

获取前大梁与水平面间的角度振动信号，通过预处理剔除前大梁抬起时的数据，获得前大梁平放状态下的角度振动信号；

(2)运用改进AMD法提取角度振动信号的超低频趋势项。

前面已提到待提取的超低频趋势项通常为信号中0.001 Hz以下的极低频率成分，因此取fc=0.001 Hz，令二分频率ωb1=2πfc，根据式(1)对角度振动信号进行解析模态分解，求出频率低于fc的信号成分x1(t)，再根据式(2,3)对x1(t)进行滑动平均，得到角度振动信号的超低频趋势项A(t)。其中，解析模态分解过程中的端部效应采用镜像延拓算法[10]进行抑制，滑动平均的窗口长度k经实验优选后取101;

(3)根据大车轨道顶部高低差与超低频趋势项间的关系模型，求出大车轨道顶部高低差。

在前述上海海事大学提出的状态监测方案中，确定了大车轨道顶部高低差ΔD(t)满足以下关系：

ΔD(t)=α(A(t)-A0)

(4)

式中：t—时间；A0—大车轨道顶部高低差为0 mm时岸桥前大梁与水平面间的角度值；α—大车轨道顶部高低差灵敏度。

根据该方案中的方法，事先对监测对象所在的码头进行现场测试和计算标定，即可确定参数A0和α，进而得出大车轨道顶部高低差ΔD(t)与超低频趋势项A(t)间的关系模型；将上一步骤中得到的超低频趋势项A(t)代入关系模型中，即可得到大车轨道顶部高低差ΔD(t)。

大车轨道顶部高低差与角度振动信号的超低频趋势项之间的关系模型能事先确定，因此，运用改进AMD法提取角度振动信号的超低频趋势项A(t)是整个方法中的关键，其性能决定了整个方法的性能。

3 仿真信号处理及结果分析

为考察改进AMD法在大数据量情况下提取超低频趋势项的性能，笔者构造出如下仿真信号：

y=x1+x2+n

(5)

式中：xi(i=1,2)—正弦信号分量，x1=sin(2πf1t)，x2=sin(2πf2t)；n—随机噪声。

取f1=0.1 Hz,f2=0.000 5 Hz，那么分量x2则为仿真信号的理论超低频趋势项。令fc=0.001 Hz，设置仿真信号的采样频率fs=100 Hz，信号时长为2 h，即采样信号长度N=720 000。

笔者分别运用原始AMD法、笔者提出的改进AMD法、小波包分解(WPD)法以及经验模态分解(EMD)法，对仿真信号的超低频趋势项进行提取。其中，原始AMD法和改进AMD法均取二分频率ωb1=2πfc，原始AMD法直接将由式(1)计算得到的信号成分作为信号的超低频趋势项，改进AMD法则取滑动平均的窗口长度k为101，将对x1(t)进行滑动平均后的结果作为信号的超低频趋势项；WPD法将包含频率成分大于指定频率fc的小波树节点系数置零，然后对小波树重构，以重构信号作为信号的超低频趋势项；EMD法将频率成分小于指定频率fc的固有模态函数之和作为信号的超低频趋势项。

各方法趋势项提取结果对比如图2所示。

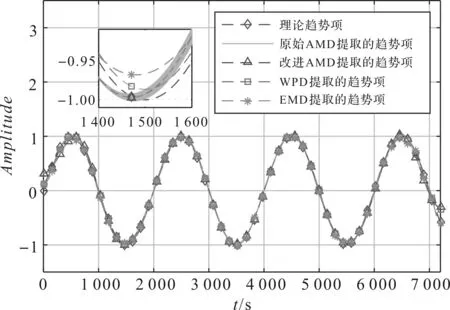
图2 各方法趋势项提取结果对比

从图2中可以看出：(1)与原始AMD法相比，改进AMD法成功抑制了原始AMD法提取结果中由随机噪声引起的随机起伏；(2)从形态来看，改进AMD法的提取结果与WPD法和EMD法的提取结果都与理论趋势项非常接近，3种方法都有效地提取出了仿真信号中的超低频趋势项。

笔者进一步考察改进AMD法的性能，以提取结果与理论趋势项间的相关系数和提取趋势项的消耗时间作为性能指标，对改进AMD法和WPD法、EMD法的性能进行定量对比分析。

首先，固定采样信号长度，分别运用3种方法对不同采样频率的信号进行处理，对比分析3种方法的性能受信号采样频率的影响情况。

此处以采样信号长度N=200 000为例，3种方法相关系数随信号采样频率变化的情况如表1所示。

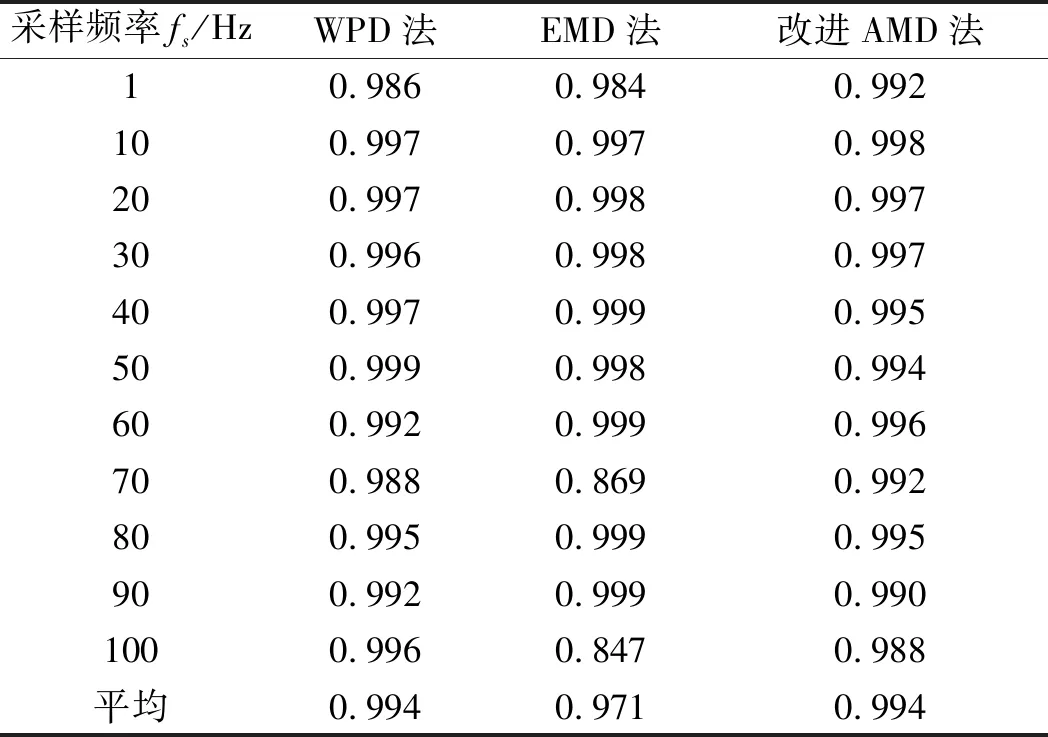
表1 N=200 000时3种方法相关系数随采样频率变化的情况

从表1中可以看出：在采样信号长度N一定的情况下，EMD法的处理结果与理论趋势项间的相关系数存在较大波动，而WPD法和改进AMD法的处理结果与理论趋势项间的相关系数随采样频率变化的波动很小，且均保持在0.99左右。

在耗时方面，3种方法耗时随采样频率变化的情况如表2所示。

表2 N=200 000时3种方法耗时随采样频率变化的情况

从表2中可以看出：(1)WPD法的耗时随采样频率提高快速增加，采样频率超过70 Hz后，WPD法耗时甚至超过2 400 s，这主要是由于采样频率增大后小波包分解层数增加造成的；(2)改进AMD法和EMD法的耗时都很稳定，且改进AMD法要明显优于EMD法。

可见，当采样信号长度一定时，运用改进AMD法提取信号的超低频趋势项受信号采样频率的影响最小。

再固定信号采样频率，改变信号时长，即改变采样信号长度，运用3种方法对不同时长的信号进行处理，对比分析3种方法的性能受采样信号长度的影响情况。

采样频率fs=1 Hz时，3种方法相关系数随信号时长变化的情况如表3所示。

表3 fs=1 Hz时3种方法相关系数随信号时长变化的情况

从表3中可以看出：随着信号时长的变化，改进AMD法的提取结果与理论趋势项间的相关系数最优，且一直稳定在0.99左右。

在耗时方面，3种方法耗时随信号时长变化的情况如表4所示。

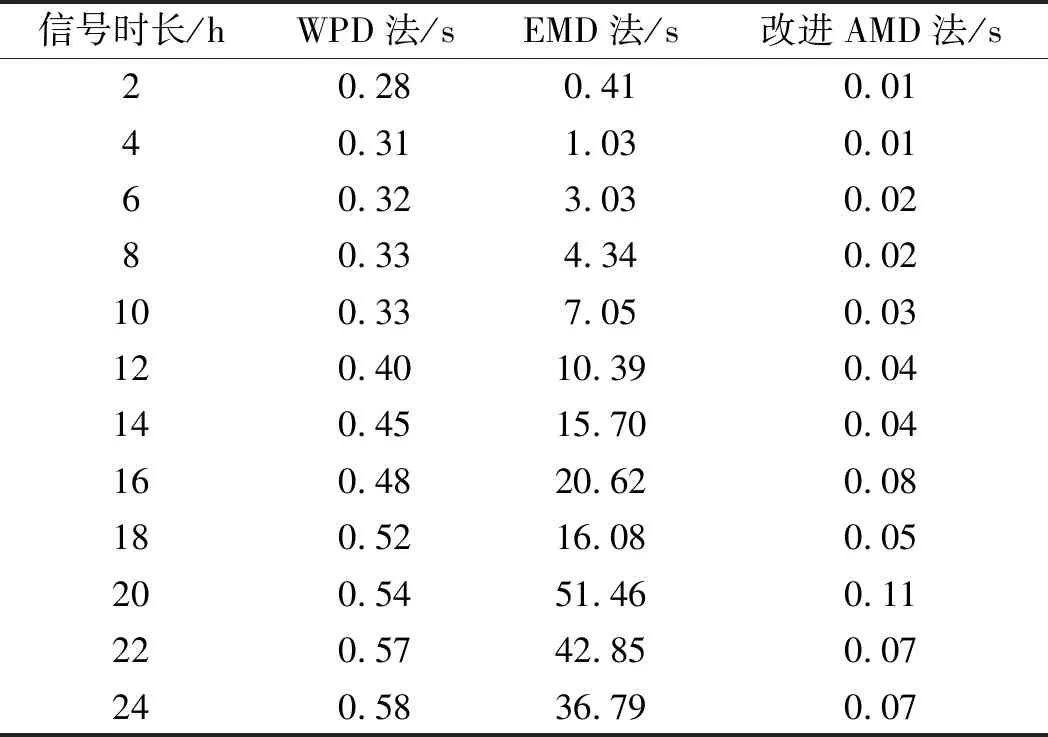
表4 fs=1 Hz时3种方法耗时随信号时长变化的情况

从表4中数据可以看出：(1)随着信号时长的增加，3种方法的耗时基本都呈上升趋势；(2)改进AMD法耗时的增长幅度最小，且耗时一直最短，最长耗时不超过0.11 s。

可见，当采样频率一定时，运用改进AMD法提取信号的超低频趋势项受采样信号长度的影响最小。

通过上述仿真实验的对比分析可见，笔者提出的改进AMD法可以很好地解决大数据量情况下的超低频趋势项提取问题。该方法能有效消除原始AMD法提取结果中，由随机噪声带来的随机起伏；而且相较WPD法和EMD法，该方法受信号采样频率和采样信号长度的影响最小，性能最稳定。

4 实测信号处理及结果分析

为验证该方法在工程实际中的有效性，笔者以某港口集装箱码头岸桥大车轨道作为研究对象，计算该码头3#岸桥大车轨道顶部高低差。

4.1 数据采集及预处理

本研究中的数据采集依托上海海事大学研发的Net-CMAS系统完成。

通过在岸桥前大梁前端布置传感器，可以监测得到前大梁与水平面间的角度振动信号。

角度信号测点位置及传感器现场布置如图3所示。

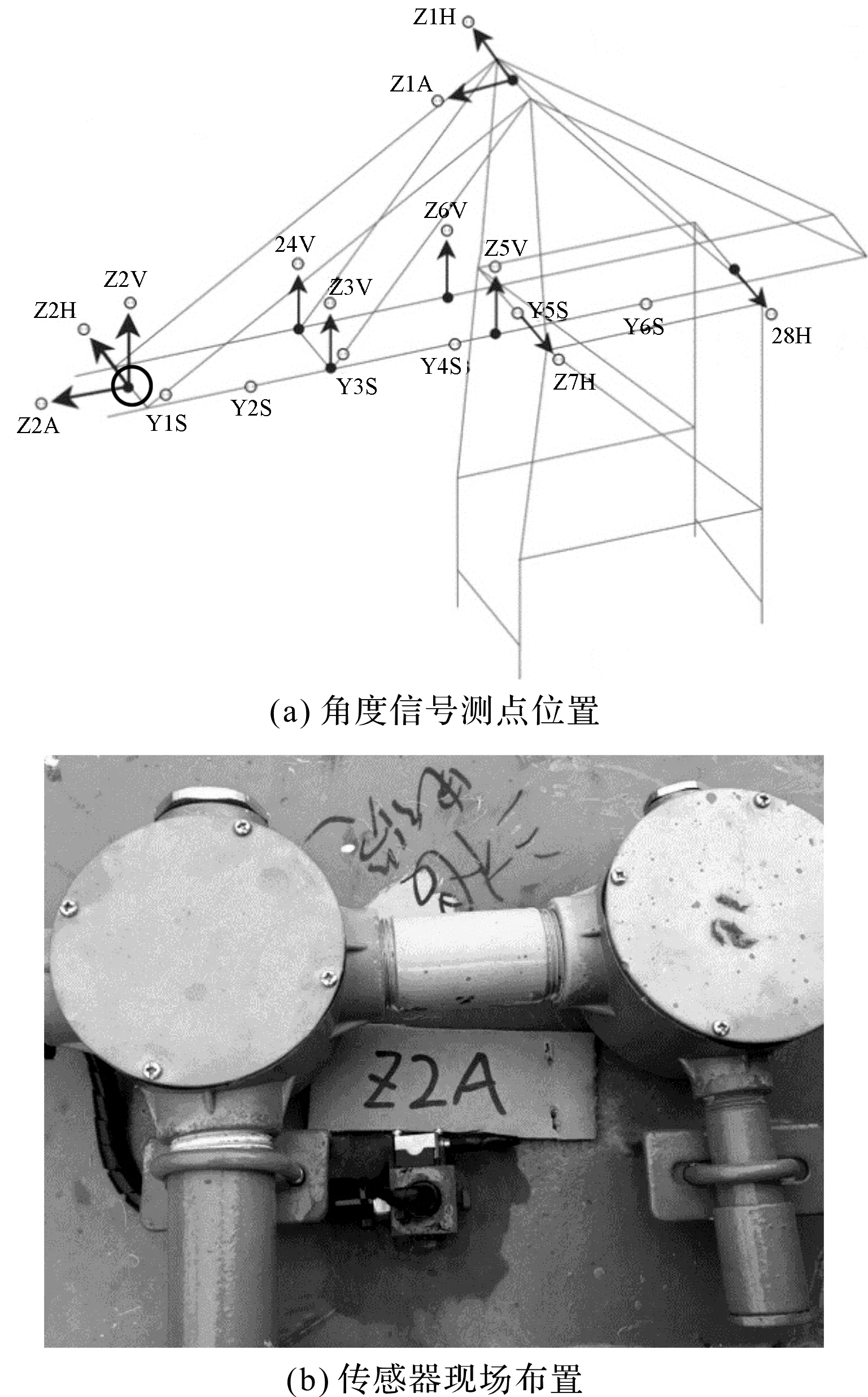
图3 角度信号测点位置及传感器现场布置

传感器测得的信号中包括岸桥在非工作状态下将前大梁抬起时的数据，前大梁完全抬起时，其与水平面间的角度比在平放状态时增加90°。

笔者根据这一特点对测得的信号进行预处理，将信号中前大梁完全抬起时对应的数据减去90°，再通过插值补足俯仰过程中的数据，可最终得到前大梁平放状态下的角度振动信号。

取3#岸桥前大梁与水平面间2019年5月其中4日的实测角度振动信号作为分析样本，经预处理后可得3#岸桥各日前大梁平放状态下的实测角度振动信号如图4所示(信号的采样频率在0.1 Hz～0.2 Hz之间)。

图4 3#岸桥各日前大梁平放状态下实测角度振动信号

4.2 超低频趋势项提取

依据前文所述，笔者取fc=0.001 Hz，信号采样频率fs=0.2 Hz，改进AMD法中滑动平均窗口长度=101；分别运用原始AMD法、改进AMD法、WPD法和EMD法对4个样本信号进行了处理，获取了每日角度振动信号中频率低于fc的超低频趋势项A(t)；从趋势项提取的准确性和处理速度两方面，对各方法的性能进行了对比。

利用各方法提取的3#岸桥各日实测角度振动信号超低频趋势项的结果对比如图5所示。

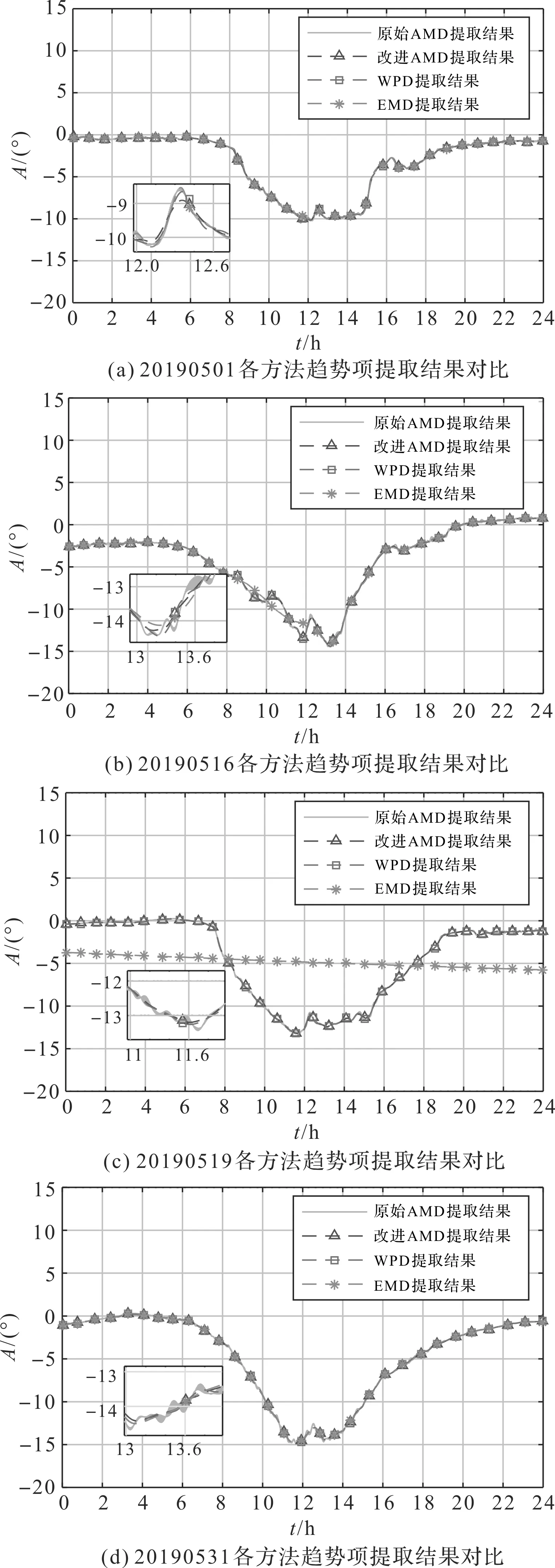
图5 各方法提取3#岸桥各日实测角度振动 信号超低频趋势项的结果对比

从图5中可以看出：改进AMD法有效抑制了原始AMD法提取的超低频趋势项中出现的随机起伏，提高了提取结果的准确度，性能明显优于原始AMD法。为此，笔者着重对比了改进AMD法、WPD法和EMD法的性能。

结合图(4,5)可以看出:改进AMD法和WPD法提取的超低频趋势项几乎一致，都准确地反映出了实测角度信号中缓慢变化的趋势；而EMD法的提取结果则出现了与实际变化趋势明显不一致的情况，如图5(b,c)所示。

可见，在趋势项提取的准确性方面，改进AMD法和WPD法的性能相近，优于EMD法。

在处理速度方面，3种方法的耗时情况如表5所示。

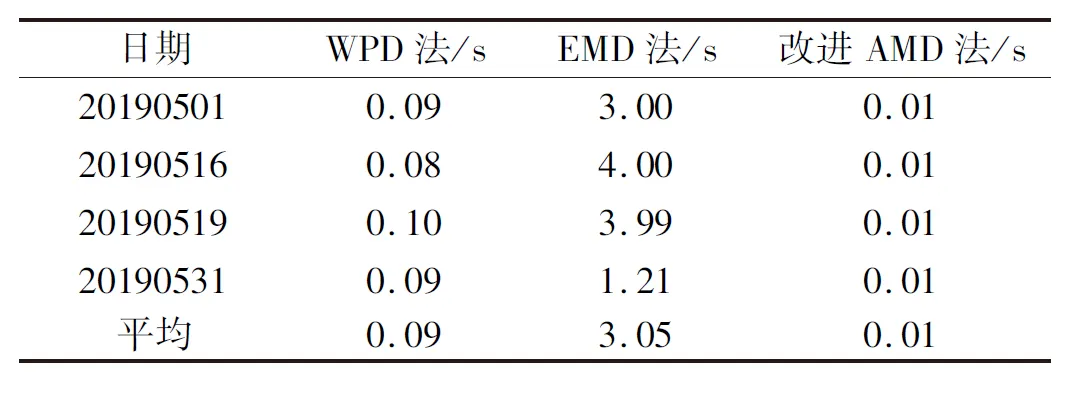
表5 3种方法的耗时情况

从表5可以看出：3种方法的处理速度都很快，但由于样本信号的采样频率不超过0.2 Hz，24 h的采样信号长度仅为7 000左右，WPD法和EMD法受采样频率和采样信号长度的影响不大，而且尽管如此，改进AMD法的处理速度仍是最快的，平均耗时仅为0.01 s。

因此，在处理速度方面，改进AMD法性能最优。

通过上述对实测信号的对比分析可见，运用改进AMD法提取实测角度振动信号中的超低频趋势项是可行的。该方法有效消除了原始AMD法提取结果中的随机起伏，提高了原始AMD法的性能，而且与现有的WPD法和EMD法相比，准确性好、实时性强，性能最优。

4.3 大车轨道顶部高低差计算

笔者事先对监测对象所在的码头进行现场测试和计算标定，确定式(4)中的参数A0和α，得到大车轨道顶部高低差ΔD(t)与超低频趋势项A(t)间的关系模型如下：

ΔD(t)=0.3A(t)-4.6

(6)

将超低频趋势项A(t)代入关系模型中，即可得到大车轨道顶部高低差ΔD(t)。如果大车轨道顶部高低差超过标准规定的±10 mm运行公差范围，则可以通过高低差变化曲线迅速确定高低差超过标准的时刻，再结合岸桥的定位系统，便可确定运行公差超标的大车轨道位置，达到状态监测的目的。

从上一小节的对比分析已知，运用改进AMD法提取超低频趋势项的性能最优，因此笔者将改进AMD法的提取结果输入关系模型，计算出3#岸桥前述几日的大车轨道顶部高低差变化情况，得到基于改进AMD法获取的各日高低差状态监测结果，如图6所示。

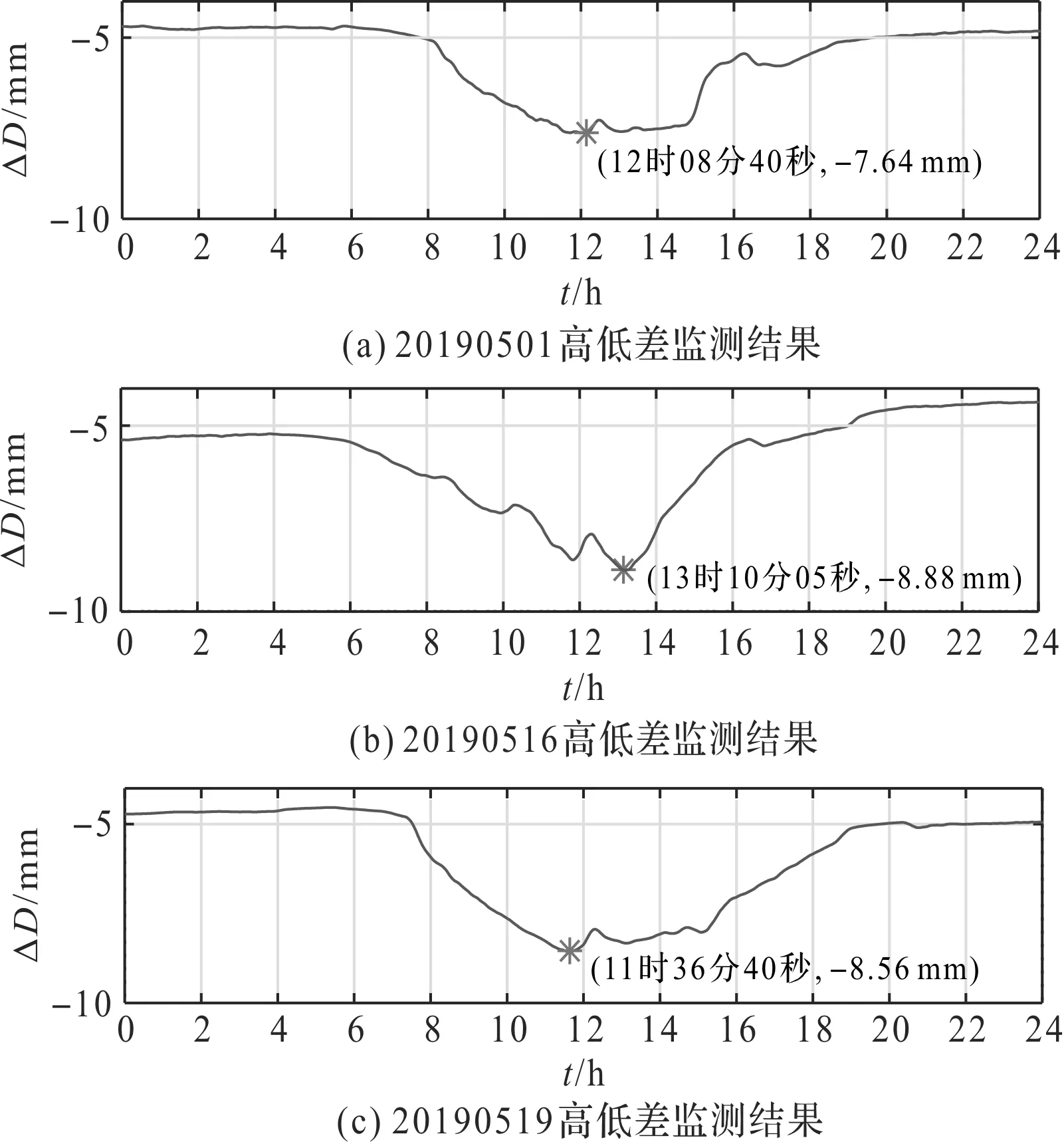
图6 基于改进AMD法获取的各日高低差状态监测结果

图6中明确标注了监测时间区间内大车轨道顶部高、低差的最大值及其发生时刻，据此可进一步判断大车轨道高、低差是否超过运行公差标准，实现对大车轨道顶部高、低差的状态监测。

4.4 长期变化趋势刻画

除了实时获取大车轨道顶部高低差的状态之外，处理长期积累的数据，刻画高低差的长期变化趋势也是工程实际中状态监测的重要任务。针对这一任务，笔者以同一大车轨道作为研究对象，获取3#岸桥2019年5月整月前大梁与水平面间的角度振动信号，运用改进AMD法、WPD法和EMD法分别进行处理，并对比3种方法的性能。

2019年5月实测角度振动信号及3种方法的高低差监测结果如图7所示。

图7 2019年5月实测角度振动信号 及3种方法的高低差监测结果

从图7中可以看出：(1)3种方法监测到的最大高低差的值及出现时刻几乎一致，高低差的整体变化趋势也十分相似；(2)3种方法的耗时分别为，WPD法0.66 s，EMD法33 861.50 s，改进AMD法0.32 s，可见改进AMD法效率最高。

虽然WPD法的耗时也很短，但工程实际中实测信号的采样频率一旦大于0.2 Hz，WPD法就需要进行更多层的小波包分解，其计算效率便会大打折扣。因此，在监测高低差长期变化趋势方面，改进AMD法的性能也十分稳定，处理效率最高。

通过实验及对比分析可见：

(1)在工程实际中，笔者提出的岸桥大车轨道顶部高低差计算方法是可行的；(2)从计算结果的准确性和计算的效率来看，相比基于WPD法和EMD法的计算方法，该方法性能更加稳定，特别是其超高的计算效率，非常适合用于监测岸桥大车轨道顶部高低差长时期内的状态变化。

5 结束语

针对岸桥大车轨道顶部高低差实时状态监测中的关键问题，即在大数据量情况下，提取前大梁与水平面间角度变化中的超低频趋势项，笔者提出了一种将原始的AMD法和滑动平均算法相结合的改进AMD法。

该方法能够有效消除单独使用AMD法时得到的超低频趋势项提取结果中由随机噪声带来的随机起伏；通过对比分析发现：改进AMD法提取超低频趋势项的性能受信号采样频率和采样信号长度的影响小，提取结果与实际变化趋势的拟合度高，通过相应的数学模型能更准确地计算出监测时间内大车轨道顶部高低差的变化情况，而且处理效率非常高。

因此，基于改进AMD法的岸桥大车轨道顶部高低差计算方法准确高效，非常适合用于获取岸桥大车轨道顶部高低差长时期内的状态变化，具有很好的实用价值。