液压摆臂履带可变形机器人的设计*

□ 孙英暖 □ 孟广耀 □ 王 哲 □ 王维信

青岛理工大学 机械与汽车工程学院 山东青岛 266520

1 设计背景

机器人能代替人类从事很多危险的工作,如消防救火、爆破排障等。机器人的行走机构一直是众多科研工作者关注的问题。机器人行走机构主要有轮式、腿式、履带式三种。其中,轮式行走机构越障能力差,不能在复杂的地形中工作;腿式行走机构行走速度有限,不能实现快速作业;履带式行走机构能适应复杂的环境,具有较快的移动速度,被广泛使用。当然,机器人履带式行走机构也有缺点,履带长时间过紧会拉长链轨节,过松会影响驱动,而且容易掉链。

目前,已有学者致力于机器人履带式行走机构的研究,并对其进行改进。朱岩等[1]利用凸轮机构,研制出履带能持续张紧且长度保持不变的SARTR机器人。文献[2]利用横纵轴双导轨,实现履带持续张紧且长度保持不变。笔者将机器人履带式行走机构的后摆臂设计为由小型液压系统结合可编程序控制系统控制,代替凸轮及横纵轴双导轨,得到液压摆臂履带可变形机器人,同样可以实现履带持续张紧且长度保持不变,同时具有较高的实时性与稳定性,保证越障时翻越障碍与履带持续张紧的同步性,极大提高了机器人的越障平顺性。

2 后摆臂构形原理

液压摆臂履带可变形机器人与不可变形机器人相比,具有更高的稳定性及越障能力,但设计也更为复杂,主要是解决如何在维持履带张紧力不变的情况下,尽量保持履带长度不变的问题。针对这一问题,笔者将椭圆定理应用于履带式行走机构的设计,使后摆臂运行轨迹为椭圆,并使用弹簧作为辅助机构,与液压系统控制相结合。

后摆臂构形原理如图1所示。

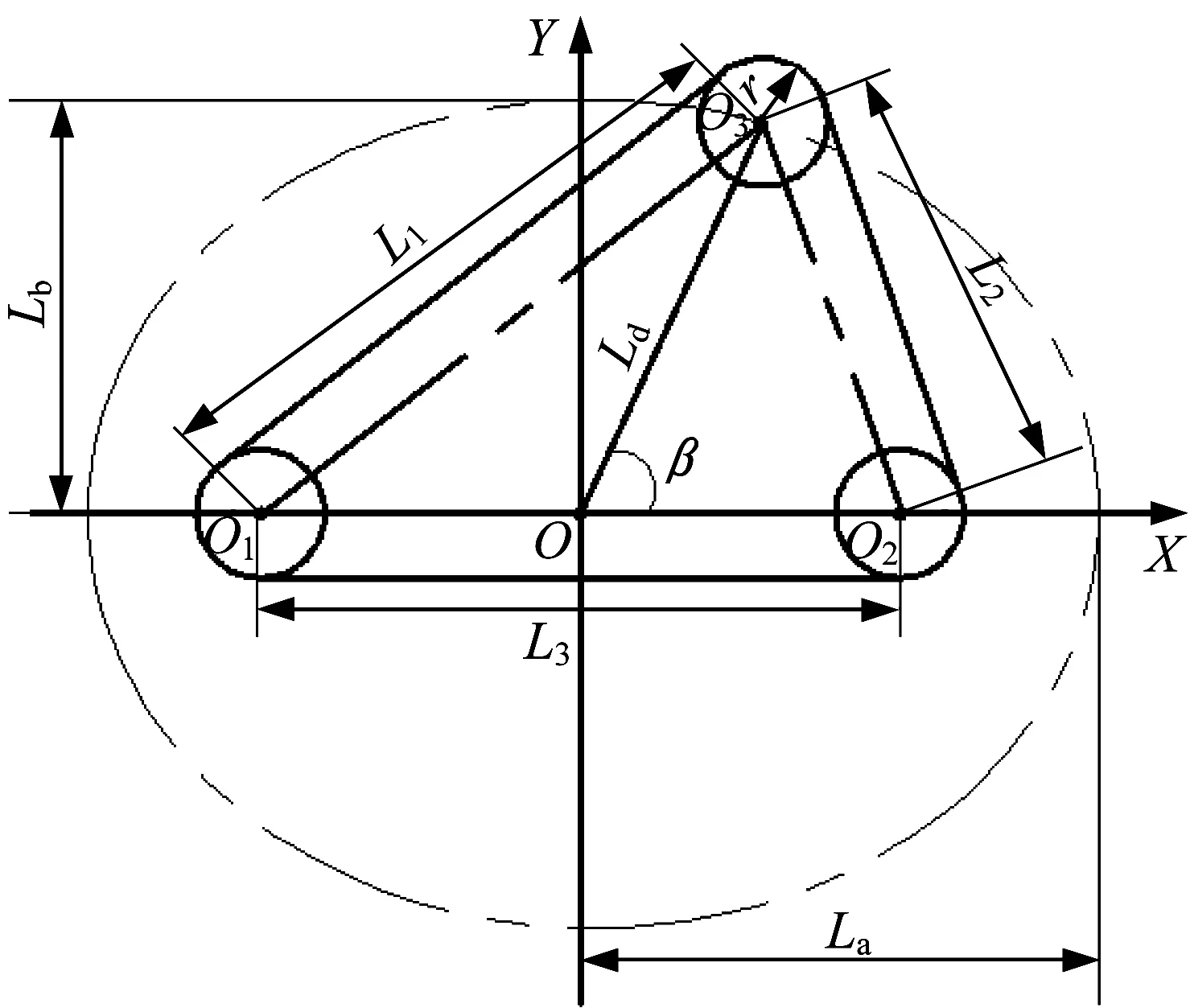
▲图1 后摆臂构形原理

主动轮圆心O1和被动轮圆心O2相当于椭圆的两个焦点,后摆臂末端轮圆心O3相当于行星轮,则O3的轨迹为椭圆。假设三个轮的半径均为r,则履带总长度L为:

L=L1+L2+L3+2πr

(1)

由椭圆定理可得:

L1+L2=2La

(2)

即:

L=2La+L3+2πr

(3)

已知La和L3为固定量,所以L为一固定值,即履带长度只与后摆臂轨迹有关,而与机器人形状处于何种状态无关。

伺服电机驱动后摆臂旋转,旋转停止后采集显示器上伺服电机的旋转圈数。设后摆臂与车体铰点为原点,后摆臂从X轴正半轴开始旋转,每一个摆臂角度对应一个电机旋转圈数,并且两者为线性关系。设电机旋转圈数为z,则后摆臂转角β为:

β=kz

(4)

式中:k为修正因数。

后摆臂构形简化原理如图2所示。

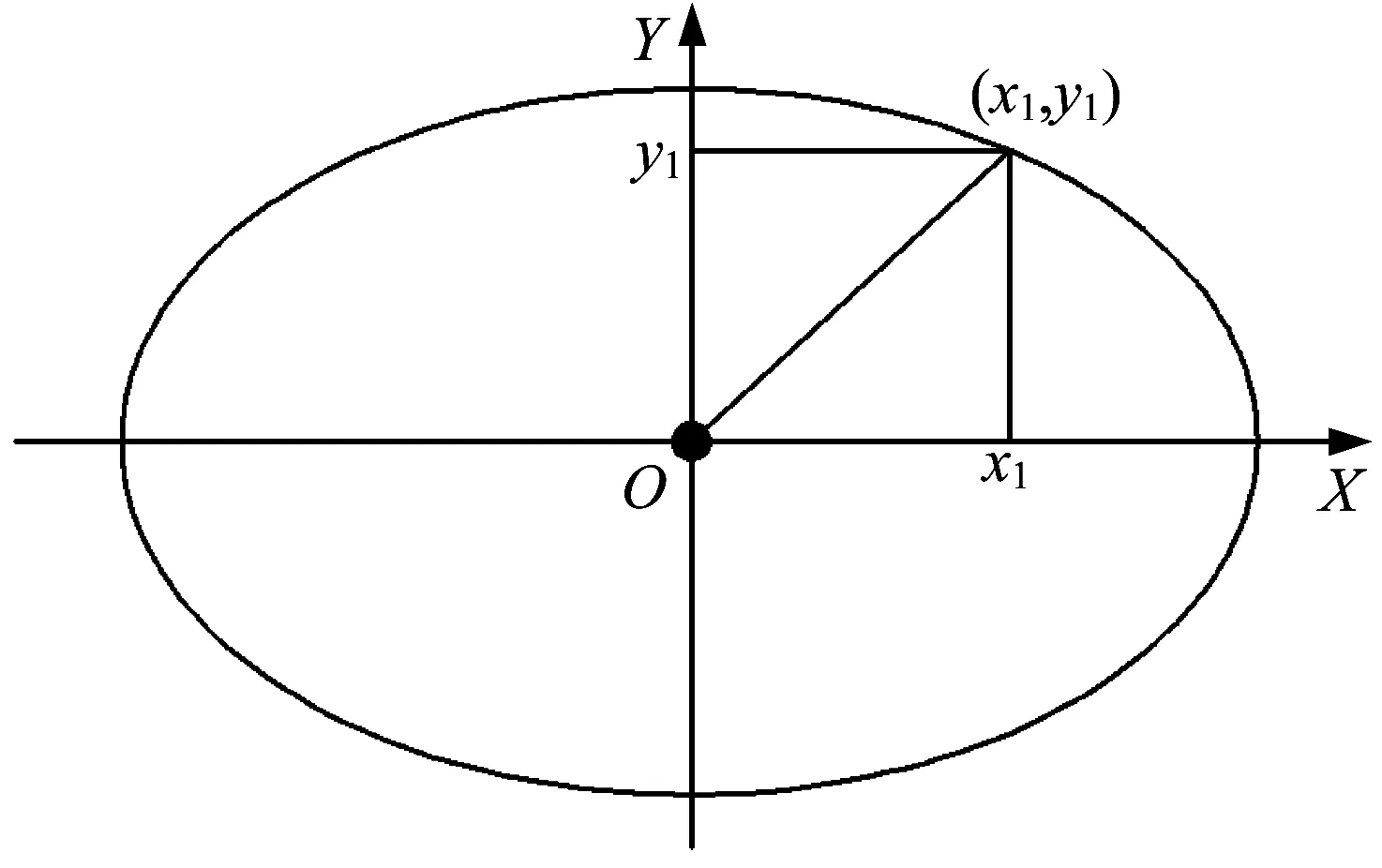
▲图2 后摆臂构形简化原理

在椭圆上任取一点(x1,y1),代入椭圆方程,得:

(5)

式中:a为椭圆长半轴,a=La;b为椭圆短半轴,b=Lb。

又有:

y1=x1tanβ

(6)

于是得到任意一点横坐标x1与后摆臂转角β的关系为:

(7)

代入式(6),得到任意一点纵坐标y1与后摆臂转角β的关系为:

(8)

后摆臂长度Ld为:

(9)

由此可见,每一个后摆臂旋转角度对应一个活塞杆位移。通过摆臂的驱动电机获取摆臂的旋转角度,数据传输到可编程序控制系统加以运算,可以得到对应的数字脉冲,控制液压伺服电机使活塞杆达到对应的位移量[3]。

3 结构设计

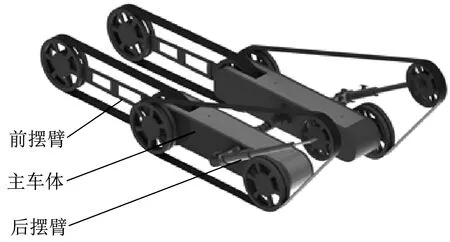
应用SolidWorks软件构建行走机构三维模型,如图3所示。前摆臂水平放置,后摆臂可实现360°旋转,两个行星轮分别位于两个后摆臂的末端。根据越障高度,可以实时调整后摆臂的角度。两个后摆臂均独立驱动。后摆臂结构如图4所示。

▲图3 行走机构三维模型

所设计的液压摆臂履带可变形机器人参数见表1。为节省空间,减轻行走机构的质量,齿轮泵选用尺寸较小的S-10型微型齿轮泵。

4 越障过程步态规划

机器人越障面临复杂地形[4],由此对应丰富的结构特征,这些结构特征由点、线、面组成。对结构特征进行分类,可以归结为台阶、凸台、沟壑、坡道、盆地等一种或多种地形的随机组合。

▲图4 后摆臂结构

表1 液压摆臂履带可变形机器人参数

对液压摆臂履带可变形机器人翻越典型地形的过程进行动作分解[5],选取后摆臂活塞杆顶端,即行星轮中心作为关键点,对每一关键步态的关键点进行受力分析,以求得活塞杆所需提供的最大推力。假设液压摆臂履带可变形机器人行走时以匀速直线运动完成越障,即加速度为零。

4.1 爬越凸台

液压摆臂履带可变形机器人爬越凸台过程,关键步态分为四步。

(1) 后摆臂抬起45°,如图5所示。此时关键点上的受力有行星轮重力G、摆臂抬高的驱动力F2、活塞杆推力F1,受力平衡方程为:

Gsin 45°=F1

(10)

Gcos 45°=F2

(11)

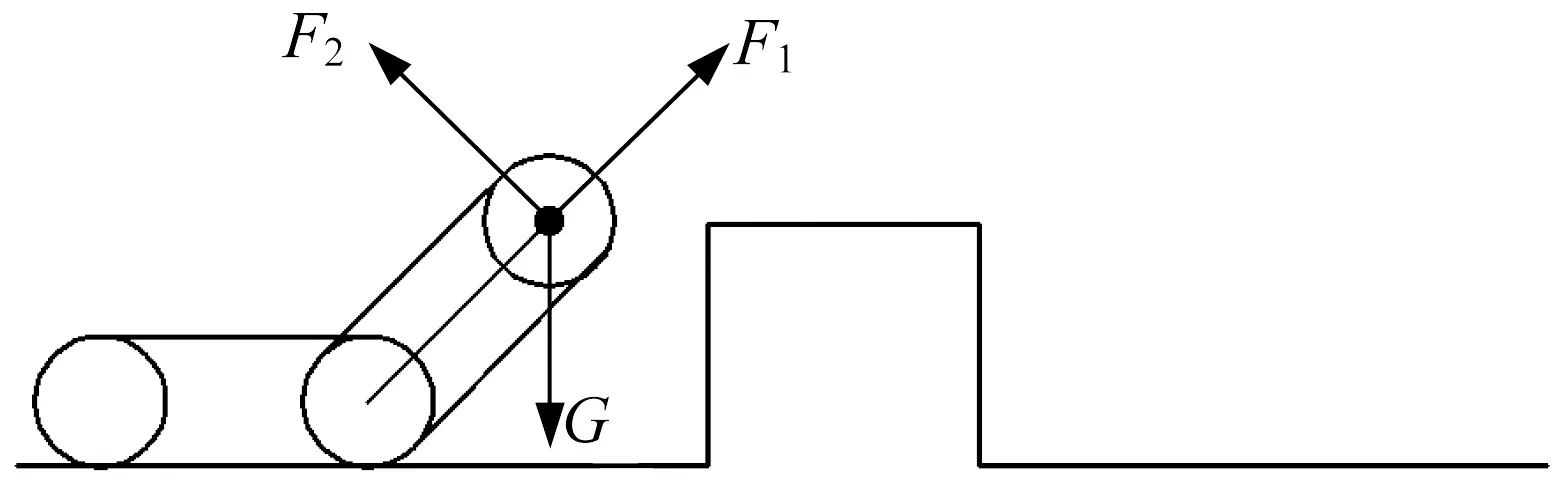
▲图5 后摆臂抬起45°

行星轮重力G为100 N,计算得到活塞杆所需提供的推力F1为70 N。

(2) 主车体靠近凸台,后摆臂搭在凸台外角线上,如图6所示。此时关键点上的受力有行星轮重力G、凸台外角线对行星轮的支持力FN、活塞杆推力F1,受力平衡方程为:

Gsin 45°=FN

(12)

Gcos 45°=F1

(13)

▲图6 后摆臂搭上凸台外角线上

行星轮重力G为100 N,计算得到活塞杆所需提供的推力F1为70 N。

(3) 后摆臂完全越过凸台外角,在凸台上平面行走,主车体呈45°趋势翻越,如图7所示。此时关键点上的受力有行星轮重力G、凸台上平面对行星轮的支持力FN、活塞杆推力F1、行星轮所受摩擦力Ff,受力平衡方程为:

FN=G

(14)

Ff=F1

(15)

▲图7 后摆臂越过凸台外角

行星轮重力G为100 N,摩擦因数取0.2,计算得到摩擦力Ff为20 N,即活塞杆所需提供的推力F1为20 N。

(4) 后摆臂呈45°搭在下平面上,主车体在凸台上平面行走,如图8所示。此时关键点承受的重力并非只是行星轮的重力,还包含一部分后摆臂的重力。对后摆臂做受力分析,后摆臂的主要受力有凸台立面对后摆臂水平向右的支持力F′N、后摆臂重力G′、凸台下平面对行星轮的支持力FN、凸台下平面对后摆臂的支持力F″N、凸台下平面对后摆臂的摩擦力F′f,受力平衡方程为:

F″N=G′

(16)

F′f=F′N

(17)

后摆臂重力G′为300 N,摩擦因数取为0.2,可得摩擦力F′f为60 N。再对关键点进行受力分析,关键点一共受到四个力:凸台下平面对行星轮的支持力FN、行星轮重力G、凸台下平面对行星轮的摩擦力Ff、活塞杆对关键点的推力F1。假设后摆臂与凸台下平面的夹角为45°,则受力平衡方程为:

▲图8 后摆臂呈45°搭在下平面

FN=G+F1sin 45°

(18)

Ff=F1cos 45°

(19)

计算得到活塞杆所需提供的推力F1为84 N。

4.2 爬越坡道

液压摆臂履带可变形机器人跨越坡道过程分为两步关键步态[7]。

(1) 后摆臂抬起搭到45°坡面上,主车体仍在坡道下平面,如图9所示。这一步态与爬越凸台第(2)步态基本相同,活塞杆所需提供的推力F1为70 N。

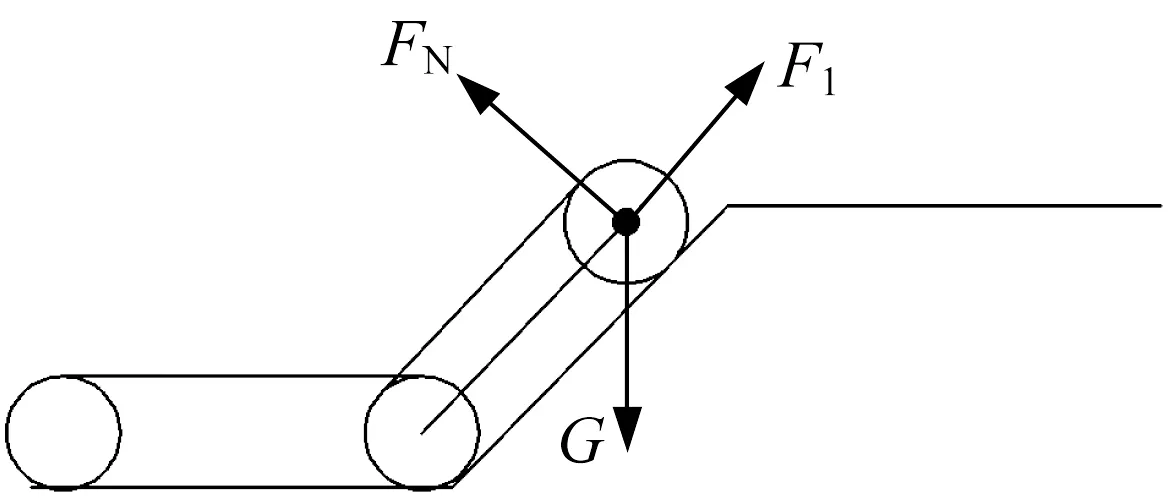
▲图9 后摆臂搭到坡面

(2) 后摆臂在坡道上平面水平行走,主车体处于坡面上,如图10所示。这一步态与爬越凸台第(3)步态基本相同,活塞杆所需提供的推力F1为20 N。

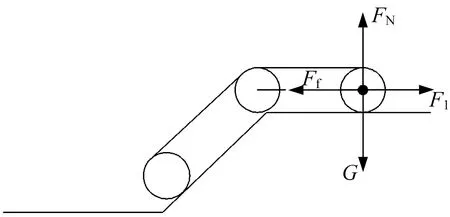
▲图10 后摆臂在坡道上平面

4.3 跨越沟壑

液压摆臂履带可变形机器人跨越沟壑过程分为四步关键步态[8]。

(1) 后摆臂落下搭在沟壑下平面上,主车体仍在沟壑上平面水平行走,如图11所示。后摆臂与沟壑下平面的夹角为45°,这一步态与爬越凸台第(4)步态基本相同,活塞杆所需提供的推力F1为84 N。

(2) 主车体完全处于沟壑下平面,后摆臂呈45°抬起,如图12所示。这一步态与爬越凸台第(1)步态基本相同,活塞杆所需提供的推力F1为70 N。

▲图11 后摆臂搭车沟壑下平台

▲图12 主车体处于沟壑下平面

(3) 主车体仍处于沟壑下平面,后摆臂搭在沟壑外角线上,如图13所示。这一步态与爬越凸台第(2)步态基本相同,活塞杆所需提供的推力F1为70 N。

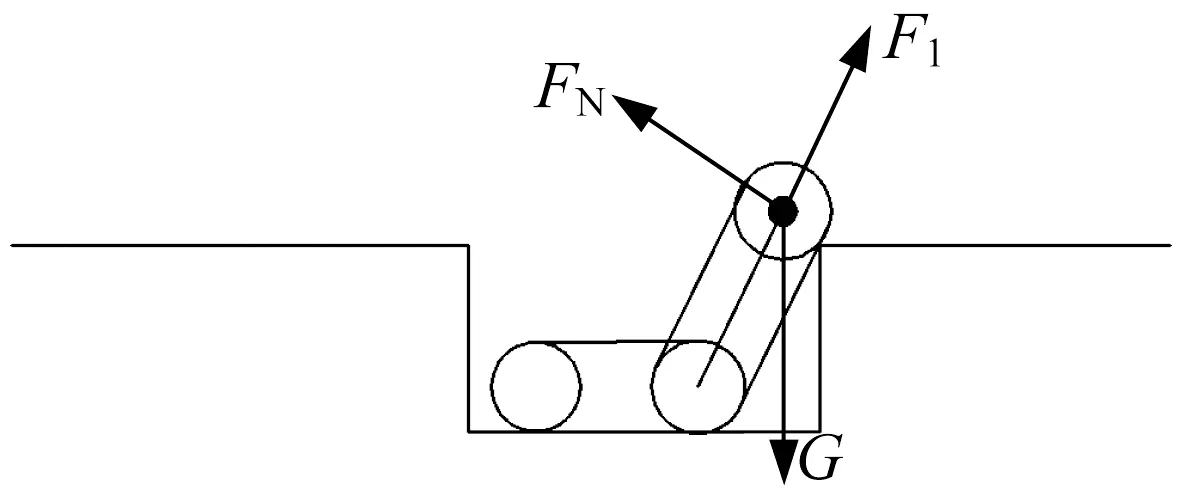
▲图13 后摆臂搭在沟壑外角线上

(4) 后摆臂完全爬上沟壑上平面,主车体呈45°爬越状态,如图14所示。这一步态与爬越凸台第(3)步态基本相同,活塞杆所需提供的推力F1为20 N。

▲图14 后摆臂爬上沟壑上平台

4.4 爬越台阶

液压摆臂履带可变形机器人爬越台阶过程分为三步关键步态[9]。

(1) 后摆臂抬起45°,主车体在台阶下平面水平行走,如图15所示。这一步态与爬越凸台第(1)步态基本相同,活塞杆所需提供的推力F1为70 N。

(2) 后摆臂搭在台阶外角线上,主车体仍在台阶下平面,如图16所示。这一步态与爬越凸台第(2)步态基本相同,活塞杆所需提供的推力F1为70 N。

(3) 后摆臂完全爬越一级台阶,水平搭在一级台阶的上平面,主车体呈45°爬越状态,如图17所示。这一步态与爬越凸台第(3)步态基本相同,活塞杆所需提供的推力F1为20 N。

▲图15 主车体在台阶下平面水平行走

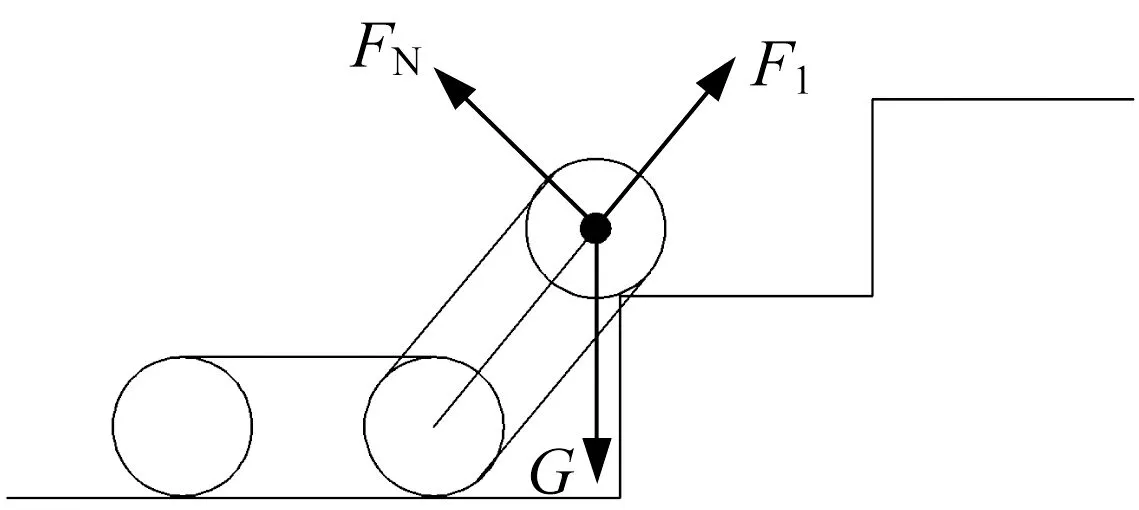
▲图16 后摆臂搭在台阶外角线上

▲图17 后摆臂水平搭在一级台阶上平面

4.5 跨越盆地

液压摆臂履带可变形机器人跨越盆地过程分为五步关键步态[10]。

(1) 后摆臂搭在盆地曲面上,主车体仍在曲面左上平面水平行走,如图18所示。后摆臂与盆地左上平面的夹角为135°,这一步态与跨越凸台第(4)步态基本相同,活塞杆所需提供的推力F1为84 N。

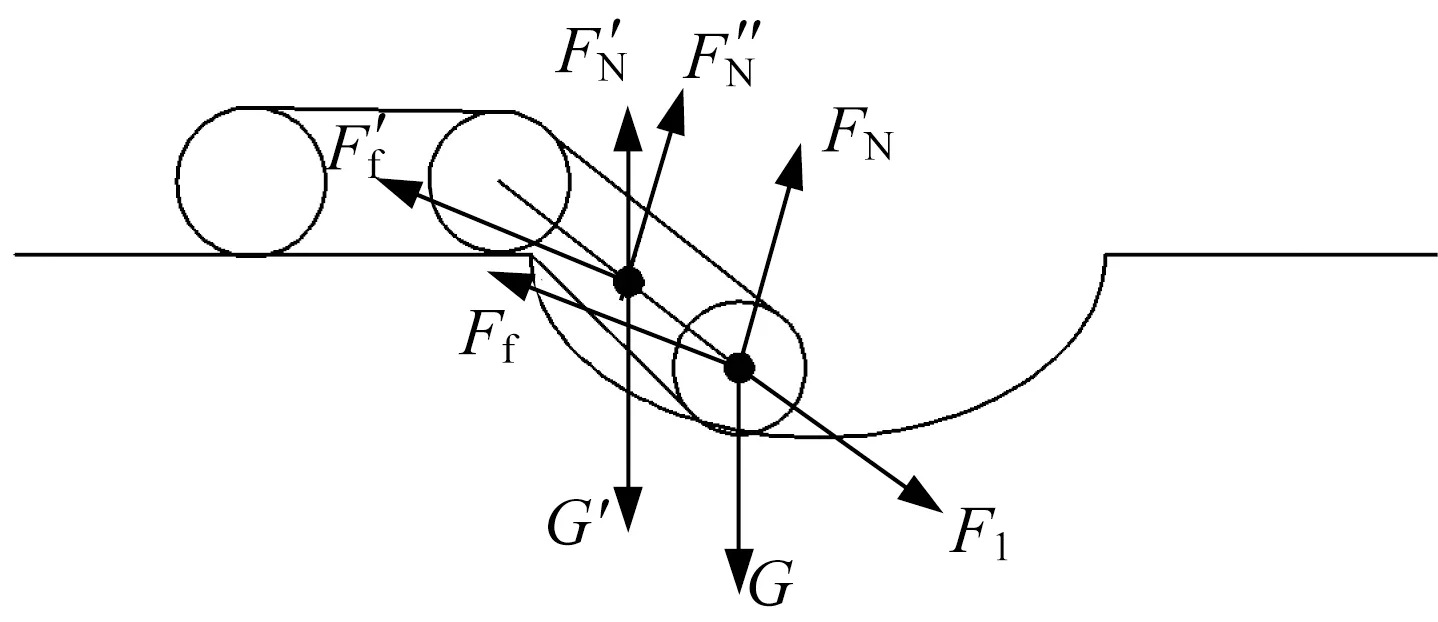
▲图18 后摆臂搭在盆地曲面上

(2) 主车体和后摆臂完全处于盆地曲面中,如图19所示。此时关键点上的受力由行星轮重力G、活塞杆推力F1、曲面摩擦力Ff、曲面对行星轮的支持力FN组成。主车体和后摆臂与盆地水平面的夹角都为30°,摩擦因数μ为0.2,受力平衡方程为:

μFN+G=F1sin 30°

(20)

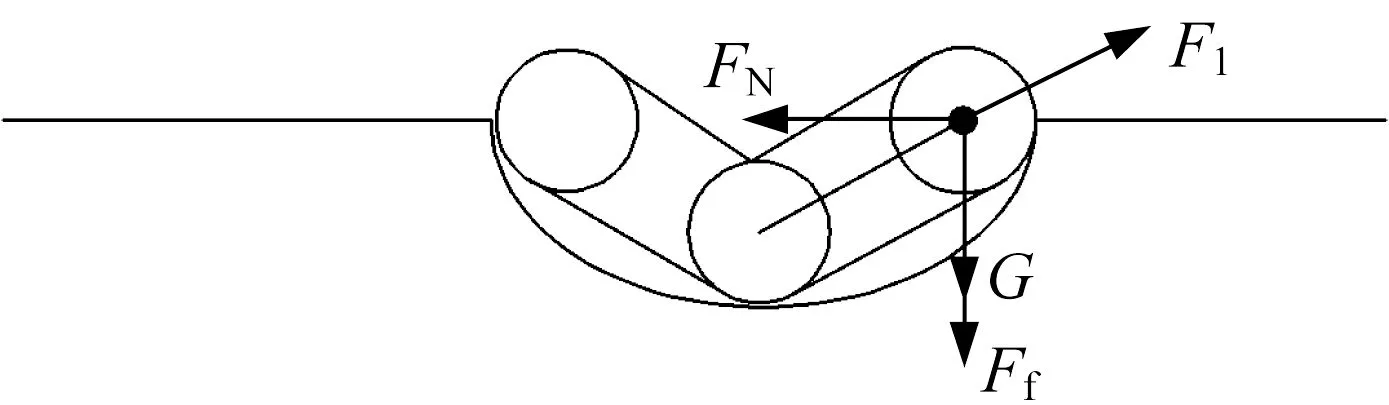
▲图19 主车体和后摆臂处于盆地曲面中

FN=F1cos 30°

(21)

计算得到支持力FN为265.5 N,活塞杆所需提供的推力F1为306.6 N。

(3) 后摆臂抬起45°,如图20所示。这一步态与爬越凸台第(1)步态基本相同,活塞杆所需提供的推力F1为70 N。

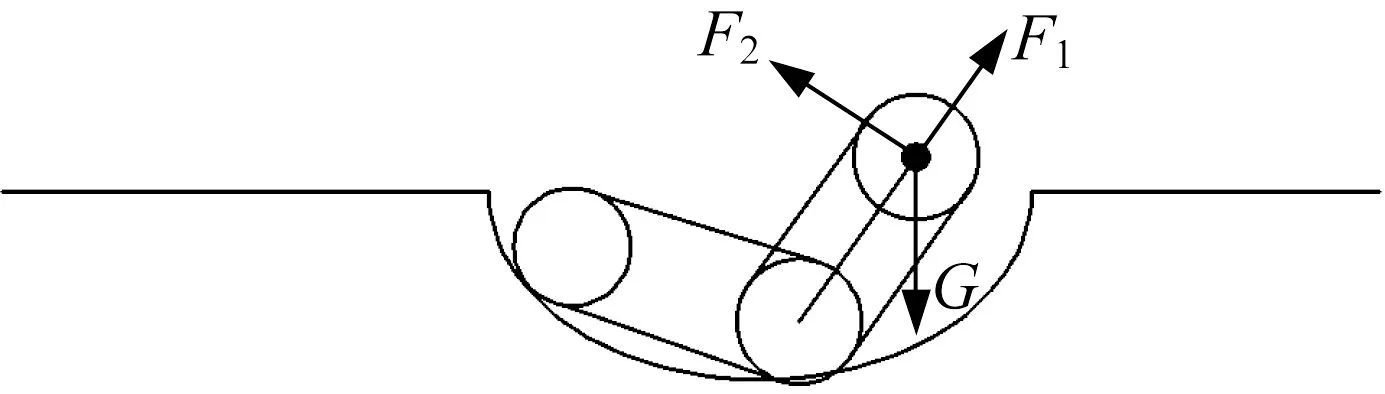
▲图20 盆地中后摆臂抬起45°

(4) 后摆臂呈45°搭在盆地右上平面与曲面的交线上,如图21所示。这一步态与爬越凸台第(2)步态基本相同,活塞杆所需提供的推力F1为70 N。

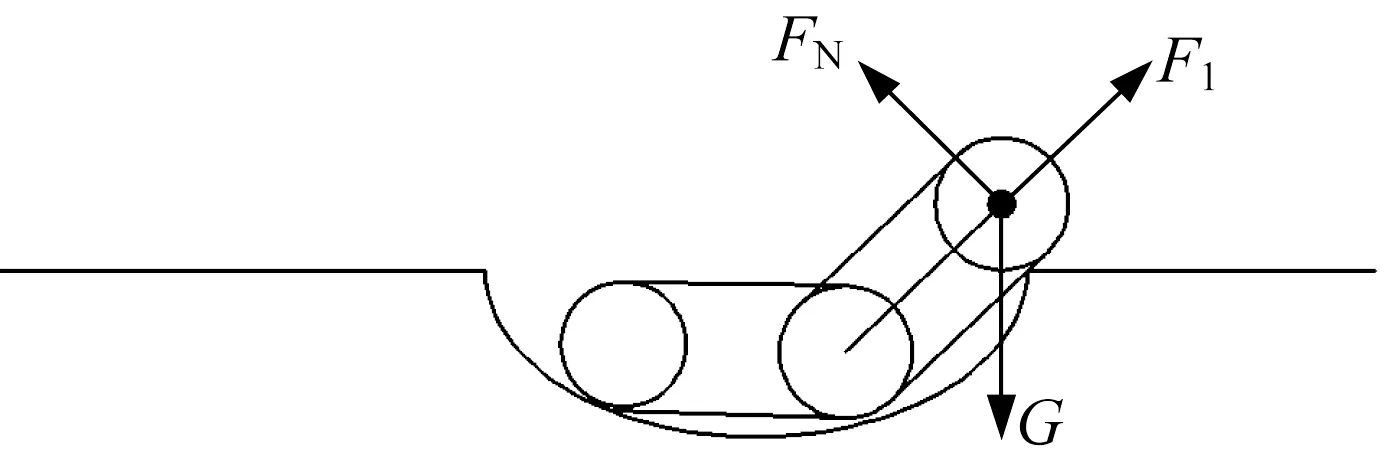
▲图21 后摆臂搭在盆地上平面与曲面交线上

(5) 后摆臂完全水平搭在盆地右上平面上,主车体仍在盆地中,如图22所示。主车体呈45°跨越状态,这一步态与爬越凸台第(3)步态基本相同,活塞杆所需提供的推力F1为20 N。

▲图22 后摆臂水平搭在盆地上平面

对所求得的各种典型地形活塞杆所需提供的推力进行比较,液压摆臂履带可变形机器人后摆臂完成越障,活塞杆所需提供的推力最大为306.6 N。

5 摆臂液压系统计算

齿轮泵流量q为:

q=Vnφv/1 000

(22)

式中:V为齿轮泵排量;n为电机额定转速;φv为容积效率,一般取0.93。

计算得到齿轮泵流量为10 L/min。

液压泵工作压力p为:

p=60P/(qφ1)

(23)

式中：P为液压泵额定功率;φ1为压力损失总效率,一般取0.79。

计算得到液压泵工作压力为1.37 MPa。

液压缸工作压力p1为:

p1=p/K1

(24)

式中:K1为系统压力损失因数,一般取1.5。

计算得到液压缸工作压力为0.91 MPa。

活塞杆额定推力F7为:

F7=p1απD2/4

(25)

式中:D为液压缸内径;α为负荷率,一般取0.8。

计算得到活塞杆额定推力为5 715 N。

活塞杆额定拉力F8为:

F8=p1απ(D2/4-d2/4)

(26)

式中:d为活塞杆直径。

计算得到活塞杆额定拉力为4 558 N。

计算得到的活塞杆额定推拉力远远大于液压摆臂履带可变形机器人跨越各种典型地形时活塞杆实际所需提供的最大推力306.6 N,设计的液压摆臂履带可变形机器人行走机构驱动系统满足要求。

6 结束语

笔者设计了液压摆臂履带可变形机器人。针对机器人行驶过程中履带不能持续张紧的问题,将机器人行走机构的后摆臂设计为由小型液压系统结合可编程序控制系统控制代替凸轮及横纵轴双导轨[11]。同时结合椭圆定理,对机器人进行了结构设计。

建立多种典型地形的数学模型,对液压摆臂履带可变形机器人的越障过程进行步态规划,对关键点进行受力分析,验证行走机构的越障性能。

所做设计为机器人履带式行走机构中履带的持续张紧问题提供了新解决思路,为后摆臂性能的研究提供了参考。