α阶强β-螺线形函数类亚历山大变换的对数导数范数上界估计
段 敏
(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;2.湖南交通职业技术学院, 长沙 410132)
万有Teichmüller空间的边界和对数螺线的自相似拟弧之间有着一种深层的关系,许多数学家建立了Teichmüller空间理论与对数导数、Schwarz导数之间的对应关系。例如,Yamashita[1-2]和Sugawa[3]分别对α阶凸函数类和α阶强星形函数类的对数导数范数的上界进行了估计。Okuyam[4]给出了β-螺线形函数类的定义,并在对数导数意义下估计了螺线形函数类的范数。冯小高等[5]构建了在Δ单页且能拟共形延拓到全平面的解析函数,简化了万有Teichmüller空间2个性质的证明。
然而,螺线形函数类亚历山大变换的对数导数范数上界估计仍不明确。郭辉[6]借助广义Schwarz引理对Landau定理中关于上界做了进一步改进并得到了一个带参数的上界表达式。Mercer等[7]得到了单位圆盘解析自映射双曲导数的Schwarz-pick估计。Patrice[8]利用双曲分差推广了双曲导数的概念,并给出了关于这些导数的Schwarz-Pick定理的类比。为此,从属函数原理出发,结合广义Schwarz引理和Schwarz-pick估计构建上界表达式。
1 基本引理[9]
引理1设f是Δ内的解析函数,且f(Δ)⊂Δ,f(0)=0,则有|f′(0)|≤1且|f(z)|≤|z|, ∀z∈Δ。若|f′(0)|=1,对于一点z0∈Δ{0},有|f(z0)|=|z0|,则f(z)≡μz,且|μ|=1。
引理2设f是Δ内的解析函数,且f(Δ)⊂Δ,ρ为Δ上的Poincarè密度,则有
ρ(f(z))|f′(z)|≤ρ(z),z∈Δ。
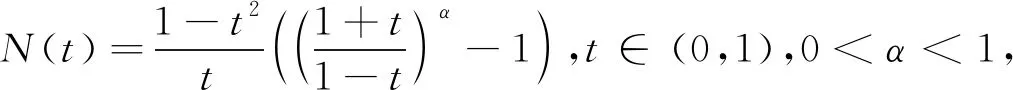
其中c(α)为方程(1-α)xα+2+(1+α)xα-x2-1=0在(1,∞)内的唯一解。
2 主要结果与证明
用S(α,β)表示α阶强β-螺线形函数类,
S(α,β)=
其中0<α<1,-πα/2<β<πα/2。
定理11)对于∀f∈S(α,β),存在常数M(α),有
‖J[f]‖≤M(α),
其中
c(α)为方程(1-α)xα+2+(1+α)xα-x2-1=0在(1,∞)内的唯一解。
2)若f∈S(α,β),
则‖J[f]‖≤M(α)γ,0≤γ<1,且γ依赖于a和函数f。
3)若f∈S(α,β),‖J[f]‖=M(α),则

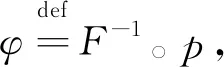
所以
故构造的函数
函数F(z)构造过程如图1所示。

图1 函数F(z)构造过程
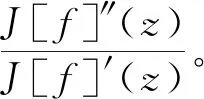
可令

所以
M(F*(|z|)-1)。
由Schwarz引理有|φ(z)|≤|z|,且F*(t)在t∈(0,1)内是一个单调递增函数,因此有
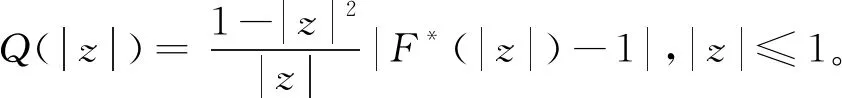

其中c为方程(1-α)xα+2+(1+α)xα-x2-1=0在区间(1,∞)内唯一的根。此时可记
其中M(α)为常数。对于M(α),Sugawa[3]给出了取值范围,
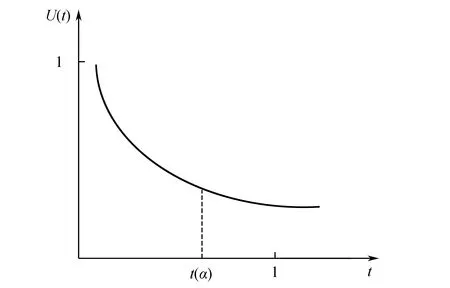
2α b)估计M的大小。作 变换,g(z)为单位圆上的自同构,且满足 由以上变换可求出 则有 因此 I≤MQ(|z|)≤M(α)。 综上可得, 2)设f(z)∈S(α,β),φ(z)=μz,|μ|=1,则 又因为 所以 两边积分可得, |φ(z)|≤|z|Q(|z|),z∈Δ, 令 求二阶导,得 又因为 f(z)=z+a2z2+a3z3+a4z4+…, 所以 f′(z)=1+2a2z+3a3z2+4a4z3+…, zf′(z)=z+2a2z2+3a3z3+4a4z4+…, 1+a2z+(2a3-a22)z2+…。 p′(0)=a2, 所以 故 ii)估计A与B。由Schwarz引理知,当|φ(z)|<|z|,z∈Δ时,|φ′(0)|<1,即 0 令 又由于φ(z)=zχ(z),故两边求导得, φ′(0)=χ(0),φ″(0)=2χ′(0)。 故有 所以 0 综上所述, 0 iii)估计‖J[f]‖。 其中z∈Δ{0}。令 则 因为0 对U(t)求一阶导可知,U(t)是在闭区间[0,1]上的单调递减函数,如图2所示。 图2 U(t)函数单调递减 由引理3知:N(t)在t∈(0,t(α))单调递增,在t∈(t(α),1)单调递减。 b)t0=t(α)时,因为U(t)在t∈[0,1]是单调递减的,所以 N(t0)U(t0)α c)当t0≠0或t(α)时,因为U(t0)α<1,所以N(t0)U(t0)α ‖J[f]‖≤M(α)γ, 0≤γ<1, 其中γ依赖于函数f和α。 基于广义Schwarz引理和Schwarz-pick估计方法,提出了α阶β-螺线形函数类亚历山大变换的对数导数范数上界表达式,得到了3个定理,推广了Schwarz导数和对数导数在Teichmüller空间理论中的应用。





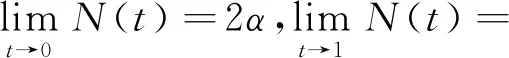
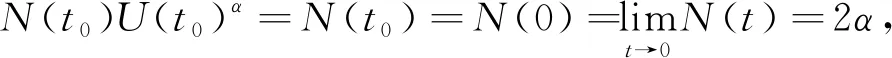
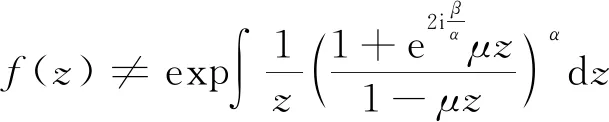
3 结束语

