Q & P钢的连续退火工艺与一次淬火马氏体相变研究

何 方 王瑞珍 杨才福 刘 鹏 吴彦欣

(1.钢铁研究总院，北京 100081； 2.邯钢技术中心，河北 邯郸 056015； 3.北京科技大学，北京 100083)

Q & P(quenching and partition)钢目前主要通过连续退火工艺生产，其热处理工艺在高温段主要分为单相区均热和临界区均热[1- 3]，在快冷和时效段的工艺则主要分为一步法和两步法[4]。单相区均热主要指连续退火的加热、均热温度超过钢的A3温度，冷却前Q & P钢主要为全奥氏体组织；临界区均热主要指连续退火的加热、均热温度介于A1和A3温度之间，冷却前钢的组织为奥氏体+铁素体。快冷和时效段的一步法和两步法工艺的主要区别在于连续退火的快冷结束温度与时效开始温度是否一致，若快冷结束温度等于时效结束温度，则称为一步法；若快冷温度低于时效开始温度，快冷结束后需再加热至时效温度，则称之为两步法。Q & P钢的连续退火工艺便于调整，单相区均热、临界区均热可以和一步法或者两步法进行组合，这些热处理方法在理论上均可实现Q & P钢的力学性能指标。

为了预测Q & P钢中残留奥氏体含量，Speer等[5]基于热力学提出了CCE(constrained carbon paraequilibrium)模型。但大量的研究指出CCE模型主要存在两个问题：一是预测的最佳快冷结束温度不准确，二是无法适应临界区退火含铁素体的Q & P工艺。这主要是由于Q & P钢连续退火工艺的灵活性，使得CCE模型计算的马氏体相变开始温度以及马氏体相变动力学规律难以在较宽的工艺窗口下与实际完全相符。因此，本文从马氏体相变开始温度的可靠性和马氏体相变动力学规律两方面出发，研究了一次淬火马氏体相变规律，建立了一种计算临界区均热条件下Q & P钢一次马氏体相变体积分数的数学模型，该模型适应了Q & P钢临界区退火含铁素体的情况。

1 试验材料与方法

试验原料取自工业连铸坯，其化学成分(质量分数，%)为：0.2C，1.25Si，2.0Mn，其余为铁和杂质元素。在马弗炉中将坯料加热至1 250 ℃并保温2 h，随后从250 mm热轧至3.5 mm厚，终轧温度为880 ℃，轧后空冷到650 ℃炉冷，模拟卷取，酸洗后冷轧成1.4 mm的板。将冷轧板线切割成20 mm×20 mm的试样，在Gleeble- 3500热模拟试验机上模拟Q & P热处理的一次淬火过程。淬火工艺参数为：以1.65 ℃/s的速率将试样加热至均热温度，保温200 s后以50 ℃/s的速率快冷到室温，均热温度分别取764、811及846 ℃。将热处理后试样切成φ3 mm的薄片，经物理减薄和电解抛光减薄制得透射电镜薄膜试样，电解抛光液成分为20%高氯酸+10%丙三醇+70%无水乙醇(体积分数)，用JEM 2100 LaBb型透射电镜观察淬火马氏体的形貌，并对其衍射斑进行标定，结合点阵常数计算得到不同临界区均热条件下淬火前奥氏体中的碳含量。在DIL805A热膨胀仪上采用与上述相同的淬火工艺模拟Q & P钢的一次淬火过程，试样尺寸为3.5 mm×3.5 mm×10 mm。最后根据热膨胀试验数据获得马氏体相变开始温度。

2 适应于临界区均热一次马氏体相变模型的建立

在CCE模型中，连续冷却过程中马氏体转变的体积分数与冷却结束温度之间的关系可表示为：

f=1-exp(a×(Ms-Mq))

(1)

式中：Ms为马氏体相变开始温度，℃；Mq为冷却结束温度，℃；f为马氏体体积分数。马氏体相变开始温度一般采用根据化学成分估算的经验公式计算得到。目前大多数研究者[6- 7]认为，式(1)中的a是常数，其值约为-1.1×10-2。式(1)在指导制定碳含量较低的单相区淬火Q & P钢的连续退火工艺时较为准确，但在计算临界区均热的Q & P钢时误差较大，原因有两方面：

(1)Q & P钢在临界区均热后、淬火前的组织是铁素体+奥氏体两相。由于相变和热力学平衡的原因，此时奥氏体中的碳含量高于热处理前钢的整体碳含量。式(1)中a受不同均热温度下奥氏体中碳含量变化的影响，因此不宜看作为一个常数。

(2)Q & P钢的临界区均热温度越接近A1温度，均热时形成的铁素体越多，奥氏体中的碳含量与热处理前钢的整体碳含量差别越大，导致根据经验公式计算的Ms温度与实测值误差增大。

综上所述，奥氏体中的碳含量对马氏体相变动力学的影响是导致式(1)计算不准确的主要原因，因此明确奥氏体中的碳含量随均热温度的变化规律是本文建立一次马氏体相变体积分数模型的前提。

根据马鸣图[8]的研究，连续退火均热过程结束时，带钢处于热力学非平衡态，钢中碳原子扩散较为充分，接近热力学平衡浓度，但代位固溶元素并未充分扩散，处于热力学非平衡状态。PE(para- equilibrium)平衡模式假设的含义是在热力学平衡的过程中碳充分扩散，接近热力学平衡浓度。但代位固溶合金元素未充分扩散，且代位固溶合金元素和铁元素的原子比不变。Q & P钢采用连续退火工艺，在淬火前所达到的热力学状态与热力学PE平衡模式描述的状态吻合。本文根据PE平衡模式计算了Si的质量分数为1.25%、锰的质量分数为2.0%的Fe- Si- Mn- C四元系相图的A3线，以计算临界区均热结束时奥氏体中的碳含量。为了易于工程应用，通过式(2)对计算所得的A3线温度进行拟合。

Xr=A1×exp(-T/t1)+y0

(2)

式中：T为临界区均热温度，℃；Xr为临界区均热后奥氏体中碳的质量分数，%;A1、t1、y0均为常数。

根据徐祖耀[9]的研究，马氏体相变开始温度(Ms)与淬火前奥氏体的碳含量(Xr)呈线性关系：

Ms=b1+b2×Xr

(3)

式中b1、b2为拟合常数。为了更加准确地描述Q & P钢在一次淬火冷却过程中马氏体的体积分数与温度之间的关系，将式(1)改写为：

ln(1-f)=a×(Ms-Mq)

(4)

不同临界区均热条件下获得的奥氏体中碳含量不同，式(4)中的a不应作常数处理。本文假设该常数与奥氏体中碳含量呈线性关系，则可描述为：

a=b3+b4×Xr

(5)

式中b3、b4为拟合常数。

将式(2)代入式(3)、(5)，再将式(3)、(5)代入式(1)，则可根据均热温度和冷却结束温度计算Q & P钢中一次淬火马氏体体积分数，其数学模型表达式为：

f=1-exp((b3+b4×(A1×exp(-T/t1)+

y0))×((b1+b2×(A1×exp(-T/t1)+

y0))-Mq))

(6)

式中：T为临界区均热温度，℃；Mq为冷却结束温度，℃。b1、b2、b3、b4、A1、t1、y0为待拟合的常数。该模型不仅考虑了临界区均热温度对马氏体相变开始温度Ms的影响，还兼顾了马氏体相变规律常数a的影响。

3 试验结果与讨论

3.1 奥氏体碳含量与均热温度的关系

Q & P钢在不同临界区均热温度淬火得到的马氏体透射电镜形貌、衍射斑点及其标定如图1所示。图1中位错密度高的区域即为马氏体。由于马氏体晶粒取向不同，其衍射斑点表现为不同的形式，如图1(b、d、f)所示。

图1 从不同临界区均热温度淬火得到的马氏体TEM形貌及衍射斑点Fig.1 TEM images and diffraction spots of the martensite produced during quenching from different intercritical soaking temperatures

由已知的相机常数和标定的晶面指数可以算出晶面间距和马氏体的晶格常数。根据Kurd Jumov等[10]的研究，马氏体晶格畸变的程度可用于计算马氏体中的碳含量，进而推算出淬火前奥氏体中的碳含量。根据PE的计算结果，试验钢中碳的质量分数为0.2%，对应A3温度为815 ℃。当均热温度为846 ℃时，淬火前钢的组织已经完全奥氏体化，通过透射电镜测得奥氏体中碳的质量分数为0.195%。811 ℃均热时钢的奥氏体化程度为95%，测得奥氏体中碳的质量分数为0.252%。764 ℃均热时钢的奥氏体化程度为50%，奥氏体中碳的质量分数为0.370%。透射电镜测得碳含量与通过PE平衡模式计算的碳含量如图2所示，实测值和计算结果较为接近。说明PE的热力学假设适用于计算临界区均热条件下Q & P钢中奥氏体的碳含量。但当均热温度高于钢的A3温度时，钢已完全奥氏体化，式(3)和式(5)中奥氏体的碳含量Xr即为热处理前钢的整体碳含量。

根据式(2)对热力学计算结果进行拟合，式(2)中常数的取值如表1所示。

表1 式(2)中常数的拟合结果Table 1 Fitted results of constants in equation (2)

图2 淬火前奥氏体中碳含量的计算结果和实测值Fig.2 Calculated and measured carbon contents in austenite before quenching

3.2 马氏体相变与均热温度的关系

根据徐祖耀的研究[9]，通过杠杆原理处理热膨胀数据，可得到冷却过程中马氏体体积分数与冷却终止温度之间的关系。临界区均热温度为764 ℃时，Q & P钢淬火过程中马氏体相变的热膨胀曲线如图3所示。沿相变开始位置作延长线BB’，相变结束位置作延长线AA’，垂直于温度坐标的直线分别与相变开始延长线BB’、相变结束延长线AA’及热膨胀曲线C相交于FOE。根据杠杆原理，对应某一冷却终止温度的马氏体相变体积分数可用式(7)描述：

(7)

根据式(7)计算得出Q & P钢在811和764 ℃临界区均热时马氏体相变开始温度，并结合PE平衡的热力学计算结果，得到奥氏体中碳含量，如表2所示。

表2 811和764 ℃临界区均热时马氏体相变开始温度Ms与奥氏体中碳含量Table 2 Martensite starting point (Ms) and carbon content of austensite during intercritical soaking at 811 and 764 ℃

图3 764 ℃临界区均热时马氏体相变热膨胀曲线Fig.3 Thermal expansion curve of martensitic transformation during intercritical soaking at 764 ℃

结合式(3)，根据上述试验数据拟合得出在Si的质量分数为1.25%、Mn的质量分数为2.0%时，Fe- C- Si- Mn系Q & P钢中奥氏体的碳含量与马氏体相变开始温度之间的关系为：

Ms=449.896-61 262.376xr

(8)

式中：xr为奥氏体中碳的质量分数，%;Ms为马氏体相变开始温度，℃。

通过式(7)对热膨胀数据进行处理获得马氏体相变动力学数据，并按式(4)对马氏体相变动力学数据进行数学处理，获得如图4 所示的马氏体相变体积分数的对数值与温度之间的关系，可用于描述Q & P钢中马氏体的相变规律。

从图4可见，811和764 ℃均热时的马氏体相变动力学曲线并不重合，进一步说明式(4)中的常数a并不是一个定值，它随奥氏体碳含量的变化而变化。假定式(4)的常数a与奥氏体碳含量存在如式(5)所描述的线性关系，则根据图4可拟合出常数a的取值，如表3所示。

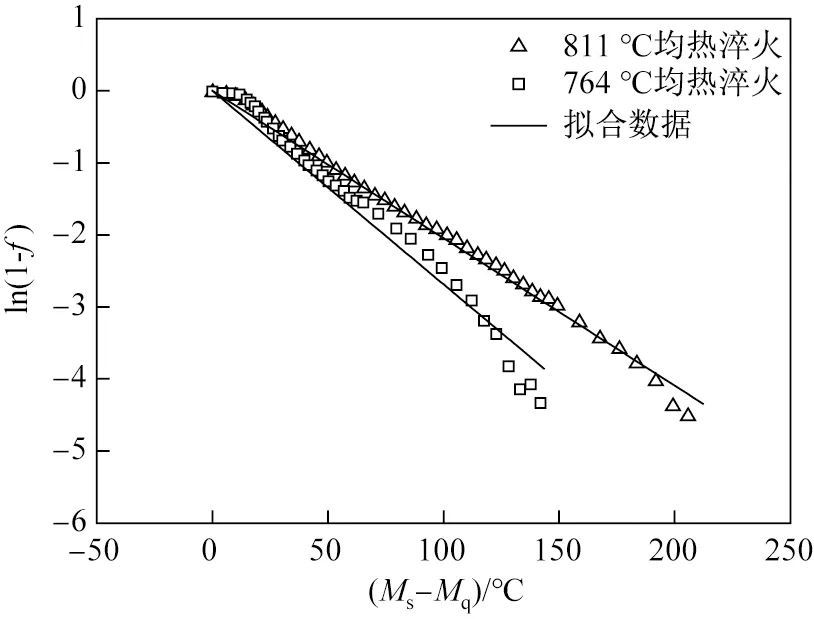
图4 马氏体相变体积分数的对数值与温度之间的关系Fig.4 Variation of logarithm value of martensitic volume fraction with temperature

表3 式(5)中常数a的线性拟合结果Table 3 Fitted constant a in equation (5)

根据表3数据对式(5)进行回归分析，得出：

a=-0.035+3.960 4xr

(9)

将式(2)代入式(8)和式(9)，再将式(8)和式(9)代入式(1)，最终得到Si的质量分数为1.25%、Mn的质量分数为2.0%的Q & P钢在不同临界区温度均热时，其马氏体相变体积分数与冷却结束温度关系的数学模型：

f=1-exp((-0.035+ 3.960 4×(6.994 38×

exp(-T/103.759 55)-7.16×10-4))×

((449.896-61 262.376×(6.994 38×

exp(-T/103.759 55)-7.16×10-4))-

Mq))

(10)

式中：Mq为冷却结束温度，℃；T为临界区均热温度，℃；f为马氏体相变体积分数，%。根据该模型对811和764 ℃临界区均热时的马氏体相变体积分数进行预测，并与实测值和文献中低碳钢模型(a值为-1.1×10-2)的计算值进行对比，结果如图5所示。

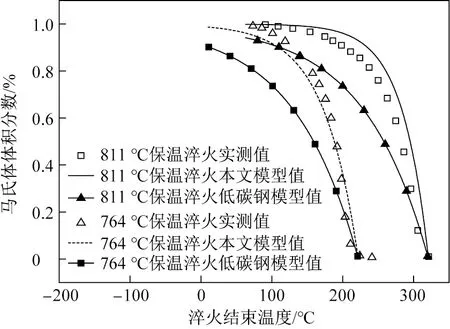
图5 不同临界区均热时马氏体相变体积分数与冷却结束温度之间的关系Fig.5 Relationship between martensitic volume fraction and quenching temperature under different intercritical soaking temperatures

从图5可以看出，如果简单按照低碳钢模型计算，计算值与热膨胀测定的马氏体体积分数偏离较大。本文通过修正马氏体相变开始温度和马氏体相变动力学规律建立的数学模型，较为准确地计算了Q & P钢临界区均热的一次淬火马氏体体积分数与冷却结束温度之间的关系。该模型极大地简化了Q & P临界区均热一次淬火马氏体体积分数的计算方法，并提高了计算精度。

4 结论

(1)Q & P钢临界区均热时奥氏体中碳含量的实测值与PE热力学平衡模式的计算结果基本一致，说明PE热力学平衡假设适用于Q & P钢临界区均热的相关热力学研究。

(2)通过修正马氏体相变动力学规律中与奥氏体碳含量相关联的两个参数a和Ms，建立了适应于临界区热处理的一次淬火马氏体体积分数与冷却结束温度关系的数学模型，该模型可用于指导Q & P钢的连续退火工艺参数的制定。