基于靶试的空空导弹自主飞可靠性置信度分析*
李根成,郭威威,李沛萱
(1.中国空空导弹研究院,河南 洛阳 471000;2.华中科技大学,武汉 430074)
0 引言
空空导弹是由飞机携带,并从飞机上发射,主要用于攻击飞机、巡航导弹等空中目标的导弹。自1958 年首次投入实战以来,空空导弹在空战中的作用越来越重要。如1973 年爆发的阿以赎罪日战争中,以色列共击落阿拉伯国家飞机336 架,除60 架被航炮击落外,其余276 架全部是被空空导弹击落;1982 年英阿马岛战争中,阿根廷被击落的32 架飞机中有24 架是被空空导弹击落;1991 年1 月17日至2 月28 日的海湾战争中,伊拉克共有38 架飞机被多国部队击落,其中被空空导弹击落36 架,被航炮击落2 架[1]。
自主飞可靠性是空空导弹极为重要的战术技术指标,描述的是自导弹离开载机后到命中目标前这一阶段工作的可靠性,其概率度量即为自主飞可靠度[2-3]。该指标倍受生产方和使用方的关注,常常在设计定型时结合靶场飞行试验对其最低可接受值进行考核,靶试结果是产品能否设计定型的重要依据[2-4]。在某空空导弹研制总要求中明确了如下自主飞可靠度指标:
1)最低可接受值:不低于0.70(置信度0.5);
2)目标值:不低于0.89(置信度0.82)。
有人提出,0.5 的置信度是否可理解为对评估出的结果可以相信也可以不相信?可靠性评估技术的研究国内外开展较多,如金碧辉对可靠性评估方法进行了全面论述,周育才对空空导弹任务可靠性、性能可靠性、单元可靠性、系统可靠性评估进行了应用研究[5-8]。但对评估置信度的研究很少,更多的是原则性的描述。以下通过分析置信度高低对评估结果的影响等疑问进行论述,首先介绍点估计与区间估计,通过区间估计引入置信度。
1 点估计与区间估计
众所周知,可靠度是统计概念,它不像产品的性能指标那样可以通过仪器仪表直接测量出来,即可靠度需要借助试验并运用统计方法加以评估[9-10]。可靠性评估是指根据样本的试验数据对总体的可靠性参数值进行估计。理论上讲,总体的可靠性参数存在真值,但常常是未知的,需根据样本提供的信息对真值进行估计,故会产生误差。估计误差的大小与样本多少有关,同样条件下,样本量越大,获取的信息越多,估计值与真值越接近[10-11]。
点估计是通过样本观测值对总体未知参数给出接近真值的一个估计值,用于估计总体参数的统计量是样本的函数,称为点估计量。用样本观测值对点估计量计算出的结果为点估计。不同估计方法给出的点估计量不同,由此得出的点估计值常常不同;即使是同一点估计量,用不同样本的观测值得到的点估计值也会不同[12-14]。
设某空空导弹自主飞可靠度真值为R,不可靠度为p=1-R,某次靶试中进行n 次独立的重复试验,用随机变量x 表示失败次数,其发生概率可用参数为n、p 的二项分布表示:

失败次数小于等于r 的累积分布函数为:
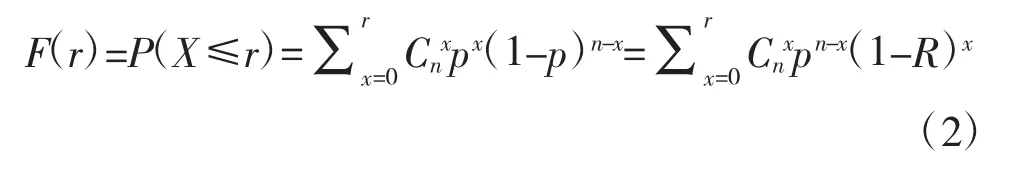
若靶试n 发中失败r 发,则产品的不可靠度点估计为:p^=r/n,可靠度点估计为R^=(n-r)/n。
如上所述,点估计有一定随机变动范围,应该加以考虑,常用方法是给出一个区间估计,这个区间以一定概率包含所估计的真值。该区间是在一定置信度下的区间,称为置信区间,区间的上、下限分别称为置信上限和置信下限。如式P(RL≤R≤RU)=γ,表示可靠度真值R 落在双侧置信区间[RL,RU]的概率为γ,RL为置信下限,RU为置信上限,γ 为置信度。式P(RL≤R≤RU)=γ 隐含有两个公式:P(R<RL)=(1-γ)/2、P(R>RU)=(1-γ)/2[15]。
2 置信度选取对置信区间的影响
显然,置信区间越窄,估计的精确性越高;置信度越高,估计的把握性越大。要同时提高估计的准确性和把握性,须增加样本量。在样本量不变时,提高置信度,置信区间就会变宽;反之,降低置信度,置信区间就会变窄。对具体的参数,我们有时并不关注双侧置信区间,而是关注单侧置信下限,如对可靠度关注其置信下限而不是置信上限,P(R≥RL)=γ;对平均修复时间关注其置信上限而不是置信下限,P(MTTR≤MTTRU)=γ。下面就以空空导弹自主飞可靠度评估为例,分析不同样本量和不同置信度下的置信下限。
如式(1)所示,自主飞可靠度真值为R 的空空导弹在n 次靶试中失败次数的概率可用二项分布描述[4,16]。真值R 虽存在,但需通过样本的观测值来评估,即通过靶试来检验导弹自主飞可靠度是否达到最低可接受值。通常是参考由最低可接受值及其置信度计算出所需靶试产品数量,并考虑需考核的战术技术性能等,最终确定设计定型靶试方案(n,r),即靶试的n 发导弹中若失败数不大于r,则判定可靠度能达到最低可接受值要求[4]。
我们要通过靶试方案(n,r)评估自主飞可靠度置信下限RL,使得P(R≥RL)=γ,也即P(R<RL)=1-γ,由式(3)确定[17-18]:
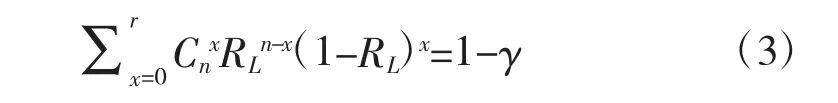
设计定型时不可能投入大量空空导弹用于靶试,所以在最低可接受值不降低时,常常不能取大的置信度。实际上,γ 小并不意味着导弹可靠性的降低,而是受试验费用等限制不能投入大量样本进行试验,不得不适当降低置信度,这从表1、表2 可看出。

表1 点估计不低于且接近0.70 时的几组数据
由表1 可知:
1)同样的试验结果,γ 越大得出的RL越小。从物理意义上可解释为:要保证可靠度真值落入置信区间的概率较大,在可靠度置信上限不变时(上限的极值为1),可靠度置信下限须降低。如靶试结果为(4∶1)即靶试4 发导弹有1 发失败的评估结果是:γ 为0.5、0.6、0.7、0.8、0.9 时的RL分别为0.614、0.556、0.492、0.418、0.320。
2)γ=0.5 时的RL仍小于R^,只是随着靶试导弹数量的增加,信息量的增大,RL与R^之差逐渐减小。如靶试结果为(4∶1)、(7∶2)、(10∶3)、(14∶4)、(17∶5)、(20∶6)时,相应的R^与RL之差分别是:0.136、0.078、0.055、0.040、0.033、0.028。
3)在产品昂贵、试验经费等资源有限不可能投入较多样本进行试验时,不能仅依据置信下限来评价产品质量,还应参考点估计。如靶试结果为(4∶1)、(7∶2)、(10∶3) 时的R^分 别为0.750、0.714、0.700,即可靠度点估计逐渐减小。但其可靠度置信下限却相反,如γ=0.5 时,靶试结果为(4∶1)、(7∶2)、(10∶3)时的RL分别为0.614、0.636、0.645。这种现象在靶试结果分别为(14∶4)、(17∶5)、(20∶6)时依然存在,并且γ 取0.6、0.7、0.8、0.9 时情况依然如此。
4)不论γ 取较小值0.5 或是较大值0.9,随着投入试验的样本量增加,同一γ 下R^与RL之差逐渐减小,即随着样本量的增大,RL逐渐接近R^。理论上,当样本量无限大或全数检验时,置信下限与点估计相等,即都等于理论上的真值。从表1 衍生出的表2也可看出,随着样本量增加,不同γ 下可靠度置信下限的差值逐渐缩小,即样本量较大时,置信度对置信下限的影响较小。
综上所述,在样本量不可能较大时,为保证用传统方法验证空空导弹自主飞可靠度最低可接受值,不应取大的置信度。
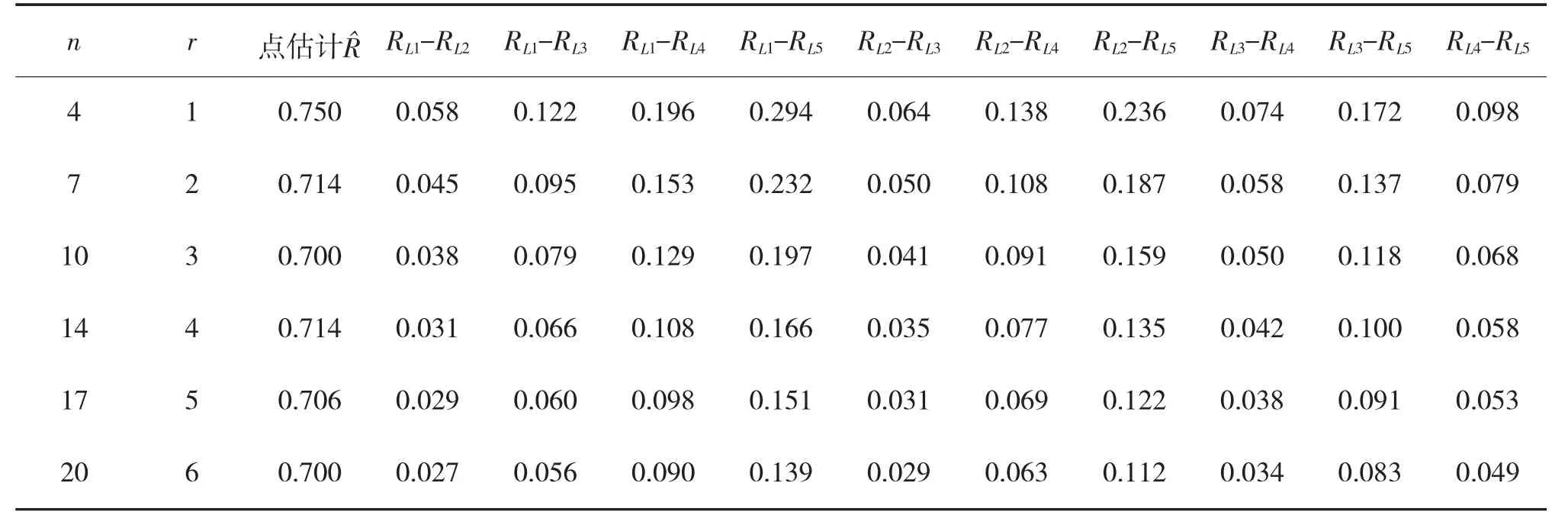
表2 不同置信度下可靠度下限的差值
表3 列出了γ=0.7 时可靠度置信下限不低于0.70 时的几组数据。(15∶3)和(26∶6)两种靶试结果得出的可靠度置信下限都是0.701,后者出现的失败数6 比前者出现的失败数3 增加了1 倍,但后者靶试的样本量26 并不是前者样本量15 的2 倍。从另一个角度看,(15∶3)得出置信度0.7 时的可靠度置信下限为0.701,若从样本量等比例增加的角度,允许失败数为4 时所需样本量为4/3*15=20。实际上,靶试结果(19∶4)中的样本量为19,小于等比例计算出的20,而实际的评估结果如何呢?由(19∶4)的靶试结果评估出RL=0.705,即样本量虽小于等比例计算出的值,但其评估的可靠度置信下限却比0.701 大。因此,不能仅依据置信下限评估产品质量,还应深究该置信下限是由什么样的靶试结果得出的,投入靶试的样本量是多少。尤其在靶试的导弹数较小时,应参考点估计值等信息综合评价其质量。

表3 可靠度置信下限RL 达到0.70(置信度0.7)时的几组数据
表4 为可靠度置信下限不低于0.70(置信度0.5)时的几组计算数据。经过与使用方就置信度对可靠度置信下限影响的专题沟通协调,考虑到需要验证的主要弹道数,设计定型时采用了方案(9,2),即靶试9 发导弹,允许的失败次数不超过2。
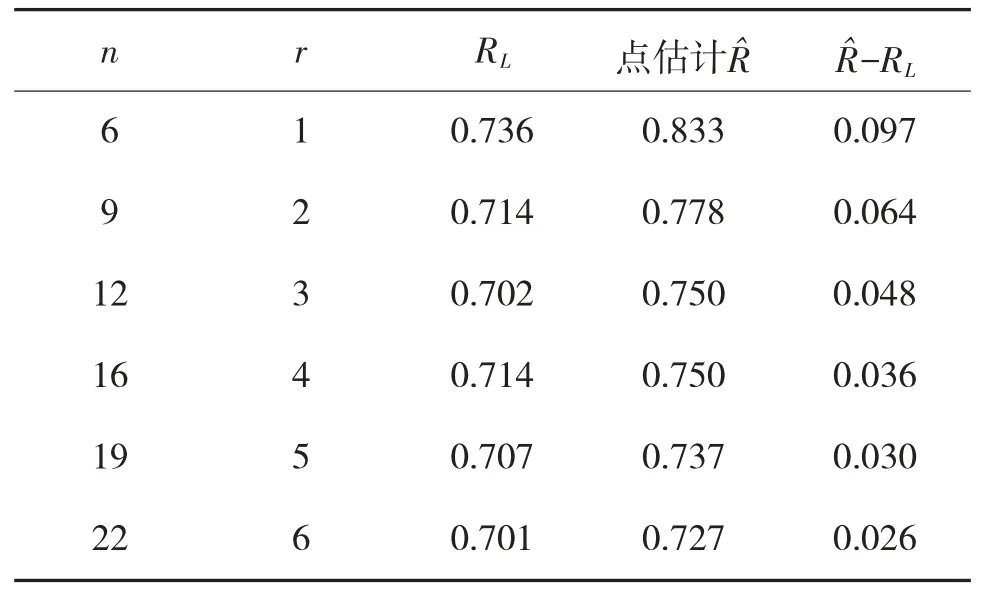
表4 可靠度置信下限RL 达到0.70(置信度0.5)时的几组数据
3 结论
按惯例导弹自主飞可靠度最低可接受值的验证,是通过设计定型时在靶场进行的导弹自主飞行试验。在允许失败次数不变的情况下,需要靶试导弹数量会随着置信度要求的提高而增加。本文重点论述了不同靶试样本量下置信度对置信下限的影响,指出随着样本量的增加,置信度的大小对置信下限的影响逐渐减小。进而说明,在限于经费等原因不能投入大量导弹进行靶试的条件下,不应取大的置信度来验证最低可接受值。取较小置信度并不是对产品可靠性要求的降低,只是受靶试导弹数量有限导致。在靶试导弹数量较小时,应考虑可靠度置信下限、点估计等信息对导弹质量进行综合评价。

