基于LMS 的多模型高机动目标跟踪方法

彭志刚，李宝鹏，李大龙

（海军航空大学青岛校区，山东 青岛 266041）

0 引言

随着现代航空技术的迅速发展，各种飞行器的机动性和运动速度越来越高，可靠而精确的跟踪目标始终是目标跟踪系统设计的主要目的与难点。目标跟踪实际上就是对目标状态的跟踪滤波问题，而实现目标跟踪首先要使所建立的目标运动模型与实际的目标运动模型匹配。

在当前目标机动能力日益增强，目标的运动模式的结构、参数变化起伏很大的情况下，单模型算法很难满足跟踪速度和精度的需求［1-3］，而多模型算法可以避免采用单模型时，由于目标机动而造成模型的不准确，提高机动目标跟踪性能，从而实现对强机动目标的精确跟踪［4］。交互式多模型（IMM）算法是利用模型先验概率和模型转移概率来计算每一个模型交互的权值［5-6］，然而，模型转移概率是人为事先确定的，它在一定程度上引入了人为误差，影响了滤波器的跟踪性能，而且，由于其对每一个模型都需要进行跟踪滤波，计算量随模型的增加而大大增加，不利于实时计算［7-8］。

本文提出了一种基于残差反馈的多模型最优跟踪滤波算法。该算法采用多个模型交互来逼近目标的实际运动模型，通过引入残差反馈信息，根据最小均方算法（LMS）求出各个模型交互的最优权，提高模型预测的准确性，从而提高目标的跟踪性能。该方法在避免了常规方法中单一模型难以准确描述高机动目标运动，在保持IMM 算法优点的同时，还避免了IMM 算法中人为设置参数和计算量大的问题，能够有效提高目标状态估计的准确性，从而提高目标的跟踪性能。

1 基本LMS 算法原理

LMS 算法因其结构简单、计算量小、稳定性好的特点，被广泛用于雷达、声纳、系统识别、信号处理及自适应预测等领域。

LMS 算法的基本原理框图如图1 所示。其中x（n）为输入信号，y（n）为自适应滤波器对当前输入信号的估计，d（n）为期望信号，e（n）为估计信号和期望信号之间的估计误差。LMS 算法通过e（n）调整滤波器的权值，使得估计信号y（n）逼近期望信号d（n），以达到最小均方误差。

图1 LMS 算法的基本原理框图

基于最速下降法的LMS 算法迭代公式为：

2 基于LMS 最优预测模型原理

基于LMS 最优预测模型原理框图如图2 所示。其中，X（k）为k 时刻目标的状态，X＾（k+1|k）为k 时刻预测目标k+1 时刻的状态预测值，Z＾（k+1）为k+1时刻目标量测预测值，Z（k+1）为k+1 时刻目标状态的观测值。要想预测的准确，就要k+1 时刻目标量测的预测值逼近观测值，即残差Z＾（k+1）最小。由LMS 原理可知，当预测模型中的权值由LMS 确定时，此时目标状态的预测值最逼近观测值，可以达到最小均方误差，因此，称为最优预测模型。

同IMM 算法一样，选择多个模型例如选择匀加速模型、Singer 模型和“当前”统计模型等常见模型来完成对目标的LMS 最优预测。目标的状态向量为：

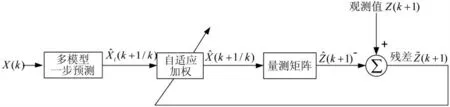
图2 基于LMS 最优预测模型的原理框图

其中，x（k）、x˙（k）和x··（k）分别表示为k 时刻目标位置、速度和加速度。例如匀加速模型的状态转移矩阵为：

其中，T 为采样周期，基于匀加速模型的一步预测为：

利用权值对得到的各个目标运动模型的一步预测值和协方差矩阵进行加权求和，得到基于LMS算法的状态估计向量和估计协方差矩阵：

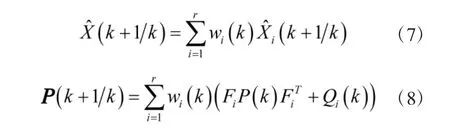
式中，r 为采用的目标运动模型的个数，wi（k）为k 时刻第i 个运动模型的权值。可以看出，目标状态的一步预测由匀加速模型、Singer 模型和“当前”统计模型等r 个模型的一步预测加权而得到，而权值由LMS 原理求出，这样就保证了目标量测的预测值与观测值残差最小，即保证了预测的准确性。

以目标机动运动为例，给出基于残差反馈的多模型最优跟踪滤波算法步骤如下：

量测的预测：

从上面的算法可以看出，本文利用LMS 原理，对多个模型的预测结果进行最优加权，通过基于最优预测结果的单模型滤波替代多模型的同时滤波，计算量也大大较少。本文所提算法的具体实现框图如图3 所示。

3 仿真分析

仿真1：假设目标的起始位置为［10 25 15］km，起始速度为［0.4 0.3 0.2］km/s，X 方向的加速度为0.15 sin（0.04πt）km/s2，Y 方向的加速度为0.1cos（0.04πt）km/s2，Z 方向的加速度为0.12sin（0.022 πt）km/s2。距离误差的标准差为△r=0.075 km，方位角误差的标准差为△θ=0.2°，仰角测量误差的标准差为△φ=0.2°。对目标进行30 s 的观测，采样间隔T为0.05。

图3 所提算法实现框图

选择的运动模型是Singer 模型、“当前”统计模型和匀加速CA 模型。IMM 与LMS 算法的初始模型权值相同，都为W（0）=［1/3 1/3 1/3］，传统IMM 算法中的概率转移矩阵P 为：

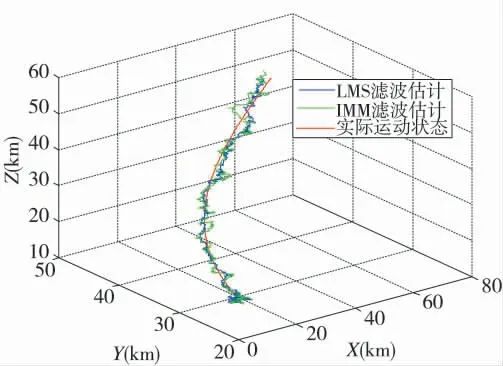
图4 跟踪轨迹图

图4 为三坐标跟踪轨迹图，可看出通过LMS 多模型跟踪方法比IMM 方法求得的跟踪轨迹更接近真实轨迹。下页图5 为目标三坐标方向跟踪误差图，可看出所提算法跟踪结果在X、Y、Z 3 个方向上都比传统IMM 方法跟踪结果误差小。

图5 跟踪轨迹误差图

仿真2：考虑到LMS 是否具有更高的普适性，研究跳跃式高超声速飞行器（高超目标）的机动跟踪情况。对雷达观测的一段飞行轨迹进行跟踪。采样间隔为0.5 s。其他参数设置与仿真1 相同。

图6 为跳跃式高超声速飞行器轨迹，图7 是图6 在高机动段的局部放大图，可以看出目标在第140～270 采样点处于大机动状态。图8 为两种算法跟踪高超目标轨迹图，可看出通过LMS 多模型跟踪方法比IMM 方法求得的跟踪轨迹更接近真实轨迹。

图6 大地坐标系高超轨迹图

图7 雷达坐标系高超目标加速度

图8 雷达坐标系高超LMS 算法跟踪图

图9 为3 个坐标方向高超目标跟踪误差图，可以看出所提方法跟踪结果在3 个坐标上整体比传统IMM 方法跟踪效果好一些，LMS 多模型跟踪结果比传统IMM 方法跟踪结果误差在目标大机动时具有更高的跟踪精度。

可见，所提方法对高速机动目标具有更好的跟踪性能，且所提方法仅仅经过一次滤波处理，在运算量上也更有优势。

图9 高超目标跟踪误差

4 结论

本文利用LMS 原理，对多个模型的预测结果进行最优加权，使得模型预测更加准确，提高了状态估计的准确性，从而提高了目标的跟踪性能。由于依然采用多模型交互来逼近高机动目标的运动模型的思想，保持了IMM 算法的优点，而且所提方法是一个带反馈的系统，能够利用前几个时刻的信息对当前时刻给出最优估计。在滤波算法上，通过基于最优预测结果的单模型滤波替代多模型的同时滤波，计算量也大大减少，也避免了IMM 算法中由于多模型带来的模型“竞争”和“冗余”问题。