基于差分进化算法的穿越走廊可行网络优化问题

李永新，甘旭升，周一叶，祝 捷

（1.西京学院理学院，西安 710123；2.空军工程大学空管领航学院，西安 710051；3.解放军95746 部队，成都 611531）

0 引言

航空军事运输在提高现代战争支援保证能力方面起到举足轻重的作用。而穿越走廊作为航空军事运输活动的载体，是指在具有全面制空权的我方控制区划设的双向空中走廊，是战场空域空中通道的重要组成部分。它可使己方航空兵运输机以最小风险通过己方防空区和受空域限制的空域，满足航空兵部队休整换防、战斗转场、人员物资空运的需要［1-2］。因此，借鉴航线网络设计概念，结合空防和空中作战任务的要求和特点，深入研究空中穿越走廊网络的优化设计问题，具有重要的理论与现实意义。

从本质上说，穿越走廊网络优化设计问题是一个航线网络优化问题。在现有相关研究中，1996 年，Gutirrez G J 等提出了基于不确定数据的无容量限制航线网络设计问题，对航线网络的鲁棒性进行了研究［3］；1998 年，Sohn J 等建立了考虑新辟航线成本的枢纽航线网络混合整数模型，提出了已知枢纽机场集合下的求解方法［4］；2008 年，赵爽建立了限制空域避让与关键节点优化相结合网络优化设计方法［5］；2013 年，王卉对考虑拥堵成本的航线网络优化设计进行了研究，并设计了相关算法［6］；2015年，王世锦等综合考虑了各种约束条件构建了航线网络优化模型，并结合元胞自动机理论对优化模型进行求解［7］。综上研究，国内外学者针对不确定环境下的航线网络经济效益作了大量研究，也采用了最优化问题求解思想，从节点交通流入手对局部航线网络进行了优化，但针对存在限制空域的航线网络优化设计较少，对航线网络的空域结构安全性优化研究还不够，更缺少从军事运输角度去研究航线网络优化设计问题。

综上分析，综合权衡约束条件，将穿越走廊网络优化问题转化为无干涉路径点布局问题，为转化的布局优化问题设计了差分进化（Differential Evolution，DE）求解算法，进而在穿越走廊网络初步规划基础上完成优化设计。实例验证了方法的有效性。

1 无干涉路径点布局模型

穿越走廊网络优化设计的关键问题在于，某一个无干涉路径点（即控制节点）的最优空间位置取决于网络中的其他无干涉路径点，因此，必须将所有无干涉路径点作为整体进行优化，使得所设计的穿越走廊网络在保证军事运输支援保障任务需求的同时，也满足战场空域限制要求。

基于上述描述，在建立无干涉路径点布局模型前，提出如下假设：

1）穿越走廊网络为二维平面网络，不考虑高度层信息；

2）节点之间的运输机为无条件直线飞行，且起讫机场对间选择网络中的最短路径作为运行穿越走廊；

3）各种类型限制空域等同看待且均不可穿越；

4）穿越走廊网络运行成本取决于各穿越走廊航段长度。

由初步规划得到的穿越走廊可行网络可表示为N（V，D，T，B），其中：

1）V（N）表示穿越走廊网络中的节点集合，包括满足空域结构或飞行需要所布设的无干涉路径点和空间位置固定不变的机场节点。穿越走廊网络中无干涉路径点和机场节点的个数分别记为n和m：

由式（7）可知，通过初始穿越走廊可行网络所经过的自由链接线后，仅需给定比例参数（h1，h2，…，hn）就可对网络进行重规划，且只要满足任意hi∈（0，1），就不会出现穿越走廊与限制空域交汇冲突的情况，既能满足穿越走廊网络的安全性要求，又可为穿越走廊网络提供可优化空间。

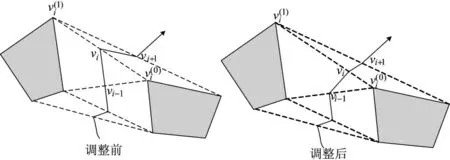
图1 无干涉路径点调整示意图

从以上最优化数学模型可看出，无干涉路径点布局优化问题可以视为不可微连续空间的函数最小化问题，存在着非线性、大规模、强约束、不确定等复杂性。因此，常规的最优化求解方法往往不是很理想，需要探索更为有效的智能算法求解该最优化模型。基于此，本文尝试采用差分进化算法求解最优化数学模型，并探讨了其可行性和有效性。

2 差分进化算法

DE 算法的基本原理是在种群中随机选取或按照一定策略选取3 个个体，将其中2 个个体的差分向量进行线性尺度变换，然后，与第3 个个体叠加以获得新个体，最后，利用目标函数对新个体与种群中预先选定个体进行评价，保留较优个体［8-9］。对于函数最小化问题：

式中，Rand 为区间［0，1］内均匀分布的随机数。

DE 算法基本操作包括变异、交叉和选择，下面进行逐一介绍。

2.1 变异操作

在第g 代进化中，选取当前种群个体xi（g），通过差分变异操作生成目标个体ti（g）。在诸多变异策略中［10］，本文选取的变异策略为DE/rand/1，其过程描述为

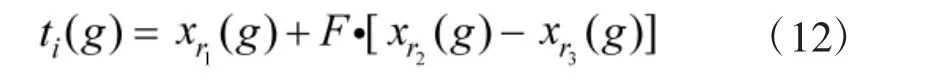
其中，rand 表示变异操作的基为当前种群中随机选取1 个个体，1 表示线性尺度变换的差分向量个数，r1，r2，r3是从［1，N］中随机选取的异于下标i 且相互独立的整数，F∈（0，1）为缩放差分向量的比例因子。图2 为二维函数优化中DE/rand/1 变异策略产生变异向量的过程。

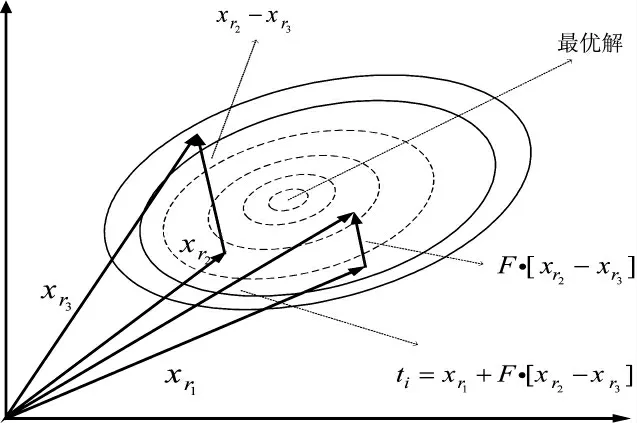
图2 二维参数空间中“DE/rand/1”变异策略

2.2 交叉操作

为改善种群多样性，需对目标个体进行交叉操作。通过将目标个体ti的部分变量替换为当前种群中个体xi中对应位置的变量，获得测试个体vi。由此可看出，交叉操作能将个体中的优良变量保留至下一代，增强了算法的局部搜索能力［11］。本文只介绍DE 算法中常用的二项交叉操作。

二项交叉操作是在区间［0，1］内随机生成若干均匀分布的rand，随机数个数等于目标个体ti中的变量个数，且各随机数rand 与变量一一对应。则可采用二项交叉操作生成测试个体vi：

式中，rnd 为区间［1，d］内均匀分布的整数，以确保至少一维分量是从ti贡献给vi；否则，可能会vi与ti相同，不利于新个体产生。图3 演示了二项交叉操作过程。

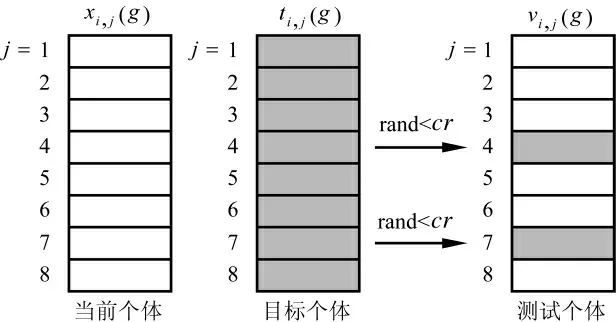
图3 二项交叉操作过程

2.3 选择操作

DE 算法采用的选择操作方式，仅当vi的适应度优于xi，才会被选入下一代。选择操作方式如下

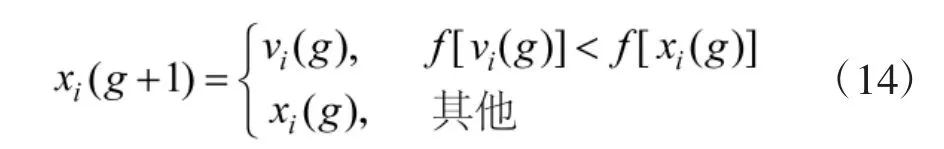
这使得更多优秀个体进入下一代种群中，通过这种逐代提高种群多样性的方法达到最优解或满意解。

为简化穿越走廊网络优化设计过程，提高优化效率，并易于算法的编程实现，本文选择最常用的DE/rand/1/bin，其中，bin 表示二项交叉操作。

3 无干涉路径点布局问题求解的DE算法设计

将DE 算法用于基于无干涉路径点布局规划的穿越走廊优化设计时，需要解决以下5 个关键性问题：1）个体的编码、解码以及各类参数设置；2）变异和交叉操作后对个体的修复，使其成为可行解；3）预置评价个体的标准；4）设计合理进化机制搜索问题的可行解，并对问题评价；5）无干涉路径点布局约束的处理。

此外，初步规划的穿越走廊可行网络为消除与限制空域之间的交汇冲突，会利用无干涉路径点进行中转，因此，也就出现了多条穿越走廊共用相同无干涉路径点的情况。这种连接方式增加了穿越走廊网络的连接度，在降低完成运输任务所需总成本的同时，也使所涉及的穿越走廊中的飞行流量大幅上升（即相当于多条穿越走廊的飞行流量汇集到一条穿越走廊中），容易造成飞行冲突，最终使穿越走廊网络的安全性下降。出于对空战场军事活动安全要求这一刚性约束的考虑，穿越走廊网络总运行成本的最小化不能依靠降低网络安全性来实现。因此，本文采用构造虚拟无干涉路径点的方法，对重复利用的无干涉路径点进行分解，如图4 所示，将该类无干涉路径点分作两个或者多个处理，尽量避免多条穿越走廊共用相同无干涉路径点的情况。

图4 无干涉路径点分解示意图

针对上述问题，基于DE 算法的无干涉路径点布局模型优化具体步骤为：

Step 1 编码

Step 6 交叉操作

对变异操作产生的目标个体ti（g），按式（13）执行交叉操作，产生测试个体vi（g）。

Step 7 选择操作

按式（16）计算vi（g）的适应度值，并按式（14）执行选择操作，生成新的种群。

Step 8 更新当前最优解

将新生成种群的个体与上一代种群中的最优个体作比较，保留比较后的最优个体，并计算其适应度值，更新best_fit 和best_ind。

Step 9 迭代

重复Step 4～Step 8，种群得到不断进化，不断更新best_fit 和best_ind，直到适应度函数最优或达到最大迭代数。

4 实例仿真

实例数据源自一次穿越走廊可行网络初始规划结果［12］（通过Dijkstra 算法求解），如图5 所示，包括10 个机场节点坐标，4 个限制空域的顶点坐标，31 个待优化的无干涉路径点（包括11 个虚拟节点）初始坐标及其对应的自由链接线，以及初步规划后的穿越走廊可行网络中各个节点之间的邻接关系。在此初始规划基础上，采用设计的DE 算法对无干涉路径点布局模型进行求解，完成穿越走廊网络的优化设计。DE 算法参数设置如表1 所示。

图5 考虑限制空域的穿越走廊可行网络初始规划结果

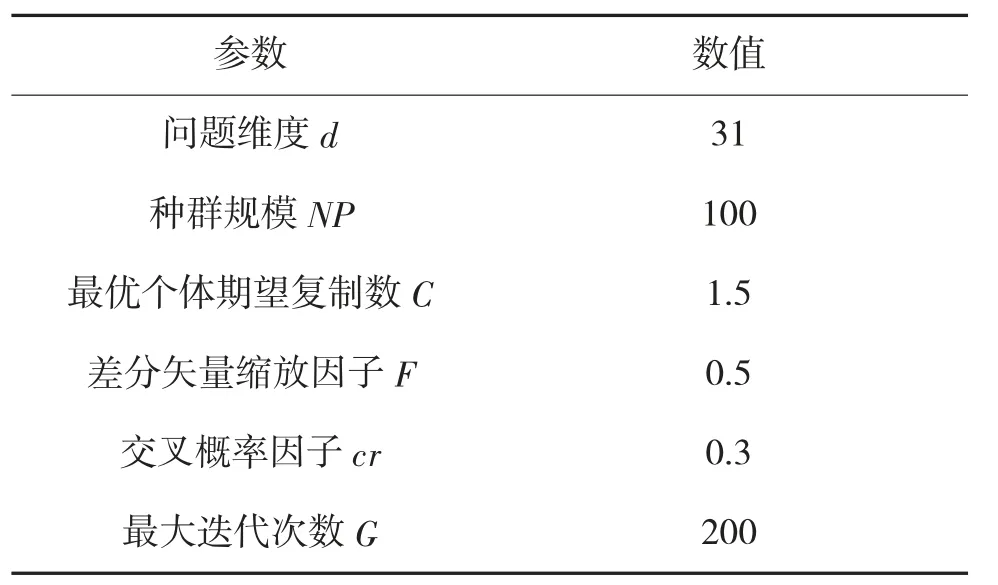
表1 DE 算法参数设置

据上述基本设置，基于无干涉路径点布局模型特点的差分进化算法用MATLAB 2014a 编程实现，对考虑限制空域影响的穿越走廊可行网络规划进行优化，优化后的穿越走廊网络如图6 所示。

图6 穿越走廊可行网络优化设计结果

在图6 中，黑色圆点为优化前无干涉路径点位置，绿色圆点为优化后无干涉路径点及其虚拟路径点位置。通过与图5 对比可看出，优化后的网络中，穿越走廊拐点减少，路径更为平滑，适合机动性相对较弱的大型运输机飞行；且穿越走廊之间出现交叉或交汇的情况也明显改善，一定程度上改善了流量拥堵的情况；网络拓扑结构也变得更为简单直观，可以明显看出枢纽轴辐式网络的基本框架。为更好说明优化效果，本文还对优化前后的穿越走廊网络性能作了定量对比。

穿越走廊网络规划设计方案要求符合航线网络指标评价体系。依据航线网络指标体系，采用网络长度、航路利用率、网络运行成本和非直线系数等具有代表性的航线网络性能指标，对优化前后的穿越走廊网络进行评价，评价结果如表2 所示。

表2 穿越走廊网络性能指标对比

由表2 中优化百分比可看出，优化后的穿越走廊网络每一项性能指标均优于初步规划的穿越走廊可行网络，其中，路径点数目减少了60%，非直线系数降低了16.5%，网络运行成本降低了12.6%，航路利用率提高了20.3 %，网络可达性提高了38.4%。通过穿越走廊网络优化前后性能指标对比定量分析，说明了优化设计方法的必要性和有效性。

5 结论

为解决穿越走廊可行网络的优化设计问题，首先，将穿越走廊优化问题转化为无干涉路径点布局问题，构建了无干涉路径点布局模型，以平衡战场空域安全与运行成本并保持在可接受的水平。然后，根据无干涉路径点布局模型的特点，设计了适于穿越走廊优化问题的个体评价标准和个体修复算子，进而采用DE 算法对无干涉路径点布局优化问题进行求解。实例分析表明，较之于穿越走廊可行网络初始规划结果，基于DE 算法的无干涉路径点布局优化的各项性能指标都得到了明显改善，将其应用于穿越走廊优化设计是可行的，也是有效的。