旋转坐标系法提高弹道直线拟合精度

李慧敏 范学祯 于贵龙 杜自成

(西安电子工程研究所 西安 710100)

0 引言

弹道测量是武器装备试验中的一项重要内容，是武器装备效能分析的一种重要手段[1-3]。直线拟合是弹道测量数据处理的一种常见处理方式，它适用于量程短、射速快，在量程范围内飞行轨迹近似为直线的弹道目标。

最小二乘法是用于直线拟合的一种常见方法[4]，其应用的主要前提是自变量无噪声、只有因变量为随机变量。当自变量、因变量都具有误差时，直接运用最小二乘进行直线拟合，将导致较大的拟合误差。文献[5-6]将自变量、因变量中的噪声看作是对真值的扰动，其中文献[5]进行了详尽的理论分析，文献[6-7]提出了总体最小二乘法，并讨论了通过奇异值分解法进行求解的过程。文献[8]中介绍了“戴明解法”，该法以测量点到拟合直线的垂直距离的平方和的最小值作为约束条件，可以比较精确的进行直线拟合。

文献[5-8]虽然考虑了自变量、因变量均包含误差的情况，但均认为二者的误差是互相独立的，对于常见的弹道测量设备，其测量在极坐标系下完成，而直线拟合在直角坐标系下进行，坐标变换环节使得测量噪声互相耦合，直角坐标系下的各个坐标值中的误差互相不独立。当各坐标值的误差互相不独立时，直接进行直线拟合将引入新的问题，本文将对此进行分析，并提供解决思路。

1 最小二乘直线拟合的误差分布

对于雷达来说，量测一般在极坐标下进行，然后转换到直角坐标系下进行直线拟合。以两坐标雷达为例，量测值为(R,θ)，分别代表目标距离和方位。量测误差的标准差分别为σR和σθ，二者统计独立且均服从标准正态分布。由极坐标转换为直角坐标系

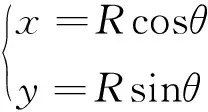
(1)

求导可得直角坐标系下坐标系的坐标值x,y的误差函数为

(2)

可见x,y均为随机变量。最小二乘的目的是根据x的测量值Xn=x1,x2,…,xnT、以及y的测量值Yn=y1,y2,…,ynT来确定x,y之间的关系y=ax+b，其中a,b为待估计的参量。总测量噪声ωi由xi的测量噪声ωxi、yi的测量噪声ωyi两部分组成

yi+ωyi=axi+ωxi+b

(3)

则

yi-axi-b=aωxi-ωyi=-Ricosθi+aRisinθiσθ-sinθi-acosθiσR

(4)

由式(4)可知，总测量噪声ωi=aωxi-ωyi。观测点xi,yi处的总测量噪声的方差为

(5)

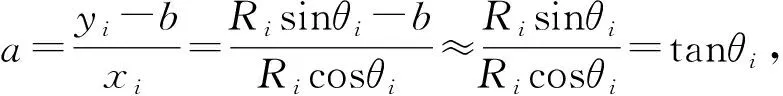
(6)

可见观测点处的总测量噪声的方差和距离Ri、角度θi有关。总测量噪声协方差矩阵Cn为

(7)

若目标角度θi随距离Ri的变化较小，即θi≈θ基本保持不变，则式(7)可进一步简化为

(8)

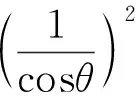
2 旋转坐标系法提高最小二乘拟合精度

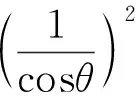
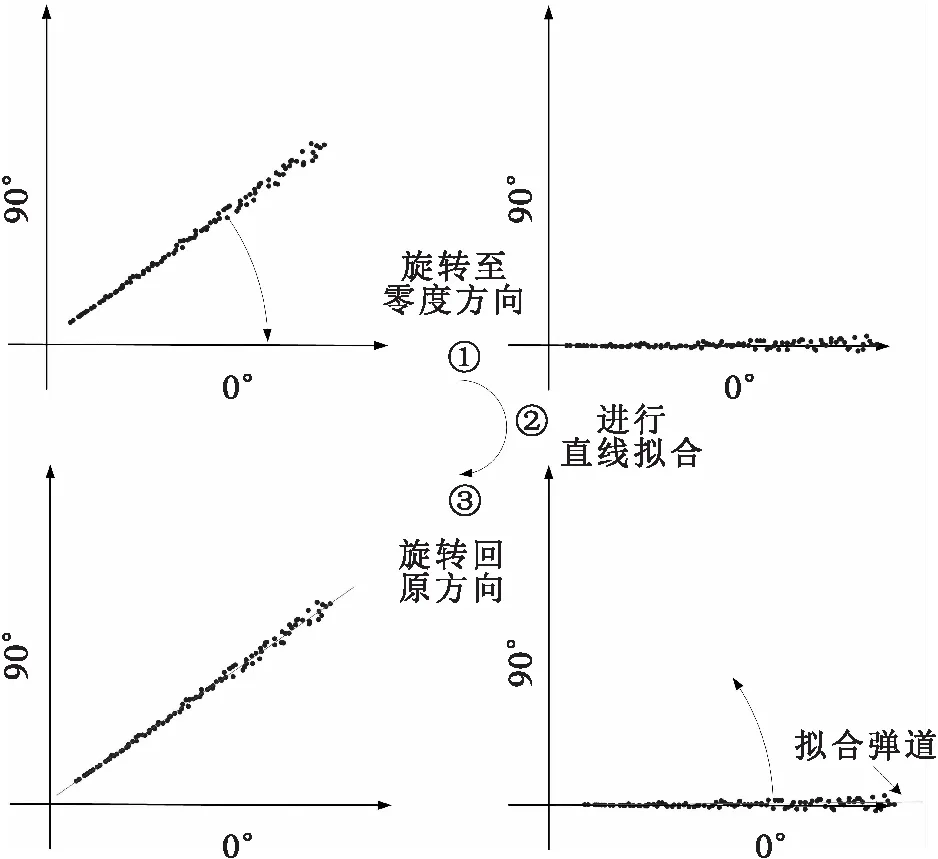
图1 旋转坐标系法最小二乘的直线拟合执行流程

旋转坐标系法最小二乘的直线拟合步骤如下：

1)求取目标角度均值α，然后在极坐标系下对测量值顺时针旋转角度α，使目标角度处于0°方向附近；

2)由极坐标系变换至直角坐标系，并进行最小二乘直线拟合；

3)将拟合结果由直角坐标系变换至极坐标系，然后逆时针旋转角度α，得到原坐标系下的拟合值。

3 仿真计算

通过蒙特卡洛仿真来验证算法性能，仿真参数设定如表1所示。

表1 仿真参数配置

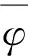
设定目标不同的飞行角度，每个角度分别进行1000次蒙特卡洛仿真。仿真结果如下：

图2中，“带◇”曲线为直接进行最小二乘直线拟合的平均偏差，较平滑虚线曲线为旋转坐标系法最小二乘直线拟合的平均偏差。目标角度越大，前者的平均偏差越大，而后者的平均偏差随角度基本保持不变且始终保持较小值。仿真结果与前文的推论相符合。

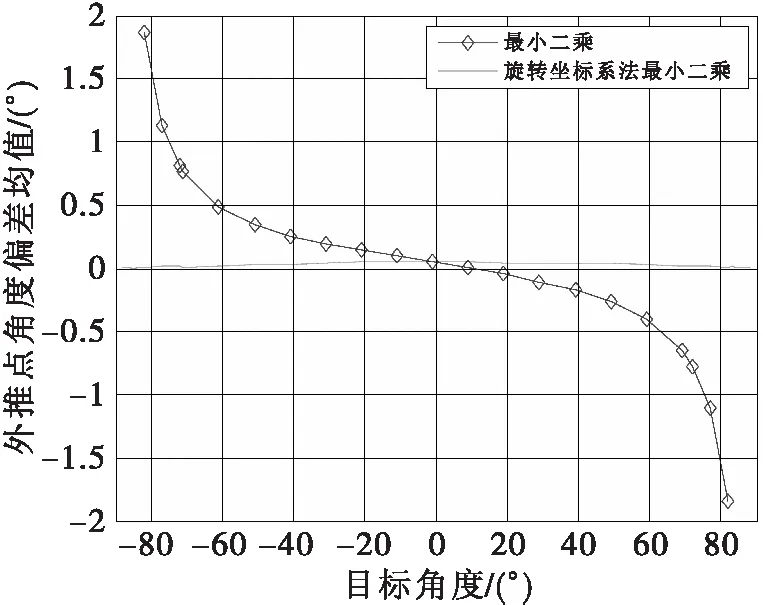
图2 外推点角度偏差均值

目标角度为75°时，两种方法的误差散布图如图3所示。

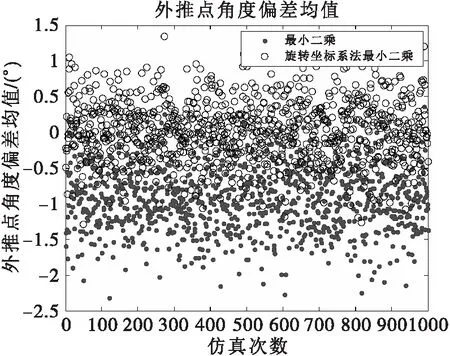
图3 两种拟合方法的误差散布图

从图3可以看出，旋转坐标系法最小二乘的误差在0°上下平均分布，属于无偏的拟合方法。而直接的最小二乘方法的平均误差偏离了0°，属于有偏的拟合方法，其拟合误差的均值大于旋转坐标系法最小二乘。

4 结束语

由极坐标系到直角坐标系的非线性变换，导致直角坐标系下的总测量噪声与目标角度相关。通过旋转坐标系法，可将直角坐标系下的总测量噪声最小化，从而提高最小二乘法的弹道直线拟合精度。仿真结果同时表明：由于直角坐标系下的各个坐标值误差互相不独立，直接的最小二乘方法为有偏估计，目标角度偏离0°越远(在-90°～90°范围内)，拟合的平均偏差越大；旋转坐标系法最小二乘接近于无偏估计，且拟合误差不随目标角度变化而变化。当目标角度接近0°时，直接的最小二乘方法的拟合平均偏差很小，因此在实际弹道测量中难以察觉出该偏差。