基于动态规划的多站雷达协同探测信号级融合算法

安政帅 刘志国

(中国电子科技集团公司第二十研究所 西安 710068)

0 引言

随着战争的不断升级和军事科学技术的飞速发展，快速发展的隐身技术和不断出现的低空高速超高速目标、日新月异的电子侦察和雷达干扰技术等，对现代雷达工作构成了巨大的威胁[1]。近几年，我国军事现代化建设的不断深入，武器装备得到了长足的发展，未来我国将会装备更多的雷达来维护我国的战略利益。目前，我国已经装备了许多同型的雷达，这些雷达目前都是独立工作的，与其它阵地或平台上的同型雷达不存在探测信息的交互。

针对单部雷达探测在频域、空域、时域等方面的局限性，为有效扩展雷达的威力范围，提高雷达的探测能力，可以选择增加雷达的功率孔径积、改进雷达信号处理技术等手段。但是，增加功率使雷达自身受到严重的安全威胁；后端信号处理改善也很有限。对于传统雷达来说，目标RCS闪烁是造成雷达性能下降的一个重要因素，但对于多站分布式雷达来说，目标RCS闪烁是可以利用来提高雷达探测性能的手段之一。研究表明，目标观测角转动一微弧度，RCS可能会变化10dB甚至更多，而传统的雷达试图最大化相干处理增益，并不能有效处理目标的RCS起伏。与传统平台上单部雷达相比，多站雷达协同探测可以充分利用目标的RCS起伏特性来大幅提升目标的探测性能，同时还具有抗摧毁、抗干扰等优势，因此，近年来成为国际雷达界的前沿研究热点之一[2-14]。

目前，国内外学者主要集中在多部雷达航迹融合算法的研究[15-19]，单部雷达通过信号级处理形成点迹或航迹，然后将单部雷达的点迹或航迹信息传送到数据融合中心进行多部雷达点迹或航迹数据的融合。这种融合方法可以大大提高对目标的跟踪精度，但是由于传输到数据融合中心的单部雷达数据已经经过门限处理，这将导致探测到的微弱目标信号的丢失，大大降低了对微弱目标的检测能力。

针对此问题，本文提出了一种基于动态规划的多部同型雷达信号级融合协同探测的新方法。该方法将多部雷达空间坐标转换后的距离多普勒数据组成动态规划算法的多帧数据，然后利用动态规划算法进行非相参信号融合处理，这样可以大大提高目标的检测性能，仿真结果表明了该算法的有效性。

1 系统模型

1.1 空间栅格划分[8]

多部雷达由于观测目标视角、观测时间以及距离尺度的不同，进行非相参积累检测，首先要进行时间维、空间维的数据对齐。以雷达距离单元和方位参数为尺度基准，对多部雷达观测区域进行栅格化划分，将多部雷达目标数据进行分类存储，方便后续信号融合处理。

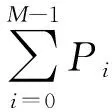
图1 雷达搜索区域空间栅格划分示意图

各节点雷达对接收的目标信号数据，根据栅格化的要求和各雷达目标的唯一性，依据各节点的相对位置信息、时间同步信息，通过坐标转换，时、空对准解算，进行目标信号数据的整理及栅格化对齐、存储。

1.2 空间坐标变换

在各雷达协同之前，每部雷达知道其他雷达在自己坐标系下的位置信息。这样，每个雷达对其他雷达送来的目标位置信息可以通过坐标变换来统一到自己坐标系下。设参与协同的雷达总数为K(K≥2)，以雷达一为融合中心，雷达k(k=1,2,…,K)为参与协同的雷达，这其中的坐标变换为：雷达k送来其观测数据信息——通过雷达k平台在雷达一的坐标位置，将观测数据信息统一到雷达一坐标系下——雷达一与雷达k(k=1,2,…,K)的信号在同一坐标系下，共同作为参与融合的原始信号。

坐标变换过程如图2所示。

图2 雷达与目标坐标关系示意图

O1为融合中心雷达，Ok为参与融合的雷达站点，T为目标。Ok在O1极坐标系下的坐标为dk,αk，目标T在各自雷达的极坐标系下的坐标为ρk,θk(k=1,2,…,K)，其中dk为雷达一与雷达k的直线距离，Rk为雷达k与目标之间的直线距离，R′k表示雷达k经上述坐标变换后距目标的直线距离；θk为目标所在方位与雷达k坐标轴之间的方位夹角，θ′k表示雷达k经上述坐标变换后所在方位与雷达一坐标轴之间的方位夹角，αk为雷达k坐标原点与雷达一坐标原点连线和雷达一坐标轴之间的夹角。

在ΔO1OkT中，由余弦定理得

(1)

在RtΔO1TH和RtΔOkTH中

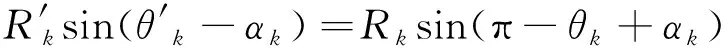
(2)

因此，雷达k与雷达一的坐标位置具有函数关系，利用式(3)、式(4)将所有雷达接收的预处理后的距离多普勒数据统一到同一坐标系下

(3)

(4)

2 多部雷达信号级融合算法[20-21]

对单部雷达而言，现代雷达信号处理技术基本都采用相参技术，但是，在目前的技术水平下，尤其对于运动平台,由于不同站点之间的时间同步精度限制，多站雷达之间的信号融合只能进行非相参积累。

2.1 数据模型

这里假设雷达一到雷达K已经完成时间同步，则对雷达一至雷达K回波数据进行预处理的过程为：对雷达回波数据进行脉冲压缩以及MTD处理，并对雷达二至雷达K回波数据按照1.2节的坐标变换公式进行空间坐标变换，变换后的数据模型表示为

zk(m,n,p)=Ak,m,n,pexp(jφk,m,n,p)

(5)

其中，k=1,2,…,K(k代表雷达编号，K表示参与协同探测的雷达总数)；m=1,2,…,M(m代表距离单元编号，M表示距离单元总数)；n=1,2,…,N(n代表多普勒单元编号，N表示多普勒单元的总数)；p=1,2,…,P(p代表方位波位编号，P表示雷达探测的方位波位总数)；这里zk(m,n,p)为第k部雷达第m个距离单元第n个多普勒单元第p个方位单元的数据值，Ak,m,n,p表示复数据的幅度值，φk,m,n,p表示复数据的相位值。

为了方便后续描述，这里将雷达一到雷达K经预处理后的数据统一表示为Z=[z1,z2,…,zK]。

2.2 状态转移原理

从理论上讲，如图3所示，各部雷达把原始数字信号经预处理后送到指定的节点进行时空配准、信号关联、信号融合、点迹检测等处理，输出目标检测信息。但是由于雷达自身定位精度和时间同步精度的限制及不同雷达观测目标的速度差异和空间坐标转换误差，融合中心进行高精度的时空配准十分困难。

为了有效实现各雷达间信号融合，将各部雷达预处理后的数据组成多帧数据，(即将多部雷达预处理后的数据分阶段进行处理)，然后利用动态规划算法进行非相参积累，实现目标的有效检测。下面讨论不同帧间目标状态是如何进行转移的。

图3 多雷达信号级融合过程

为了描述的方便，这里定义目标的状态向量xk=[rk,θk,vk]，其中rk表示目标当前的距离，θk表示目标当前所处的方位角，vk表示目标当前的速度。

为了实现动态规划算法,必须对目标的状态空间进行离散化。在1.1节中已经将雷达搜索区域进行了空间栅格划分，下面将目标的速度进行离散化，将[-vmax,vmax]进行均匀划分为2L等份，其中L=vmax/Δv，这里Δv表示速度分辨单元，这样目标的速度范围可以表示为[-LΔv,LΔv]，目标的速度可以表示为vm=-vmax+mΔv，(m=0,1,2,…,2L+1)。

假设第k帧目标所处的状态为

那么第k+1帧目标所处的状态为

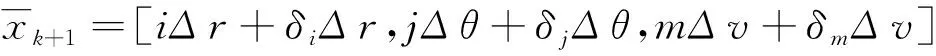
这里δi，δj，δm分别表示距离、角度和速度误差，这些误差主要是由于空间坐标转换，雷达自身定位精度等因素引起的，δi，δj，δm可以根据实际需要进行取值。

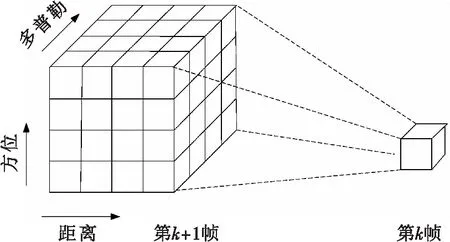
图4 帧间状态转移示意图

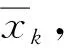
2.3 基于动态规划的多部雷达信号级融合算法[22-26]

在采用动态规划方法进行多部雷达信号级融合前，对2.1节中雷达一的数据和坐标变换后雷达二到雷达K的数据取幅值，根据数据的幅度值，构造动态规划方法的值函数，然后采用动态规划方法进行多部雷达信号级融合，流程如图5所示，最后经目标检测得到目标的距离、方位、速度等信息。

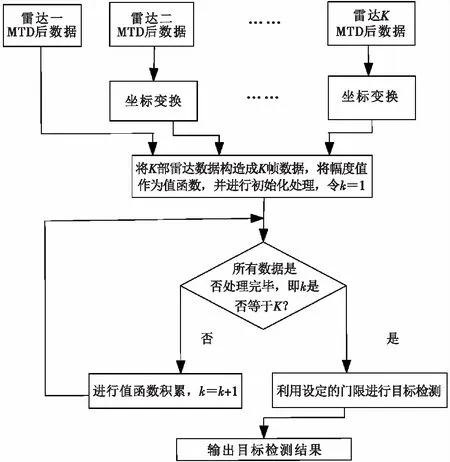
图5 多部雷达信号级融合算法流程

具体地，采用动态规划方法进行多部雷达信号融合包括以下步骤：

Step1：进行初始化处理，用雷达一取幅值后的数据作为第一帧数据，利用第一帧数据对值函数进行初始化

I(x1)=z1

(6)

其中，I(·)表示值函数。

Step2：递归积累过程，当k取2至K时，将雷达二到雷达K坐标变换取幅值后的数据作为第2到K帧数据，利用式(7)求出k帧积累后的值函数I(xk)

(7)

其中，τxk表示目标状态在k-1帧时所能转移的状态范围。

当k=K时，得出I(xK)，根据前述说明，此时I(xK)仅为xK的函数，τxk根据坐标转换误差和目标相对不同雷达的运动特性确定。

Step3：找出满足设定条件的状态，所述设定条件为I(xK)>VDT，VDT为设定门限。

3 信号级融合算法性能分析

3.1 不存在匹配误差下的非相参积累增益分析

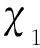
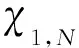
(8)

(9)

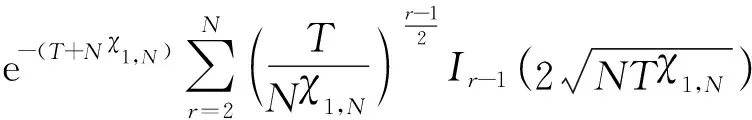
这里Person形式的不完全伽玛函数为

(10)

从式(10)可以看出该闭合解包含非常复杂的非线性运算，计算十分复杂，下面通过研究近似方法来求解其非相参积累增益。

Albersheim公式是对非起伏目标检测问题的实验性近似，但是仅仅对于线性检波器有效。单个样本SNR根据公式(11)计算。

lg(A+0.12AB+1.7B)dB

(11)

通过使用具有不同N值的Albersheim公式来计算单个样本SNR，可以容易地获得非相参积累增益。

3.2 存在匹配误差下的非相参积累增益分析

下面给出现存文献中关于动态规划非相参积累增益的分析结果，具体推导可以参阅文献[27]。

1)纯噪声区域

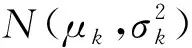
μm1=μk+σkμmax(q)

(12)

(13)

(14)

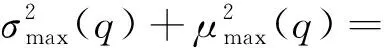
(15)

两个相互独立的高斯随机变量的均值与方差通过对这两个随机变量的均值与方差求和得到，因此

μk+1=μm1+μ=μ+μk+σkμmax(q)

(16)

(17)

2)存在信号的区域

则

(18)

(19)

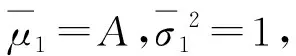
这样可以得到检测概率和虚警概率的表达式为

(20)

(21)

在存在不同匹配误差条件下，给定虚警概率，根据虚警概率的表达式可以计算出相应误差下的检测门限值，然后根据检测门限值依据检测概率的表达式可以计算不同信噪比下的检测概率，进而可以得出不同匹配误差条件下的检测性能损失。

4 实验结果与性能分析

仿真参数设置：雷达发射线性调频信号时宽5μs，带宽2MHz，采样率4MHz，雷达一和雷达二单次回波信噪比均为SNR=-18dB，相干积累脉冲数64；方位波束宽度2°，雷达搜索区域方位角度范围θ0=30°和θP=120°，两部雷达的直线距离为1km，雷达二相对于雷达一的夹角α=20°。仿真实验具体如下：

1)不存在站址误差条件下信号级融合算法仿真与分析。

从图6可以看出，利用基于动态规划的信号级融合算法实现了两部雷达的信号级融合,同时不难发现信号进行非相参融合积累的同时噪声也实现了一定的积累,由于噪声是随机的，经信号级融合后信噪比会有一定的提升，这样有利于实现对弱小目标的检测。

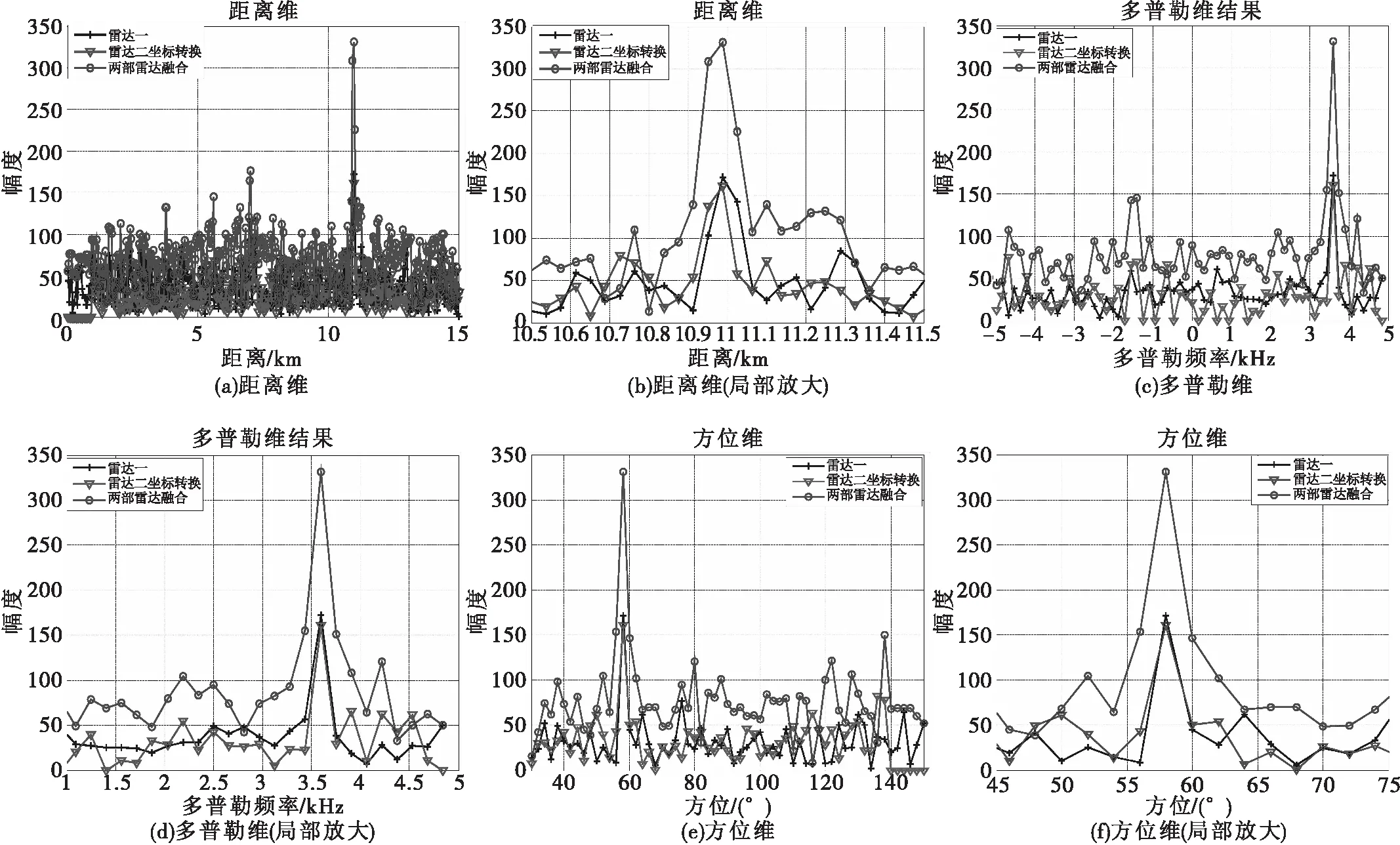
图6 信号级融合前与融合后结果对比图

2)存在站址误差条件下信号级融合算法仿真与分析。

从图7可以看出，由于雷达定位误差的存在，空间坐标转换只实现了距离维、方位维和多普勒维的近似配准，并没有实现雷达一和雷达二距离、方位和多普勒通道的完全对齐，但是利用基于动态规划的信号级融合算法仍然实现了两部雷达的信号级融合，这说明该算法具有一定的稳健性，从而为该算法工程应用奠定了基础。

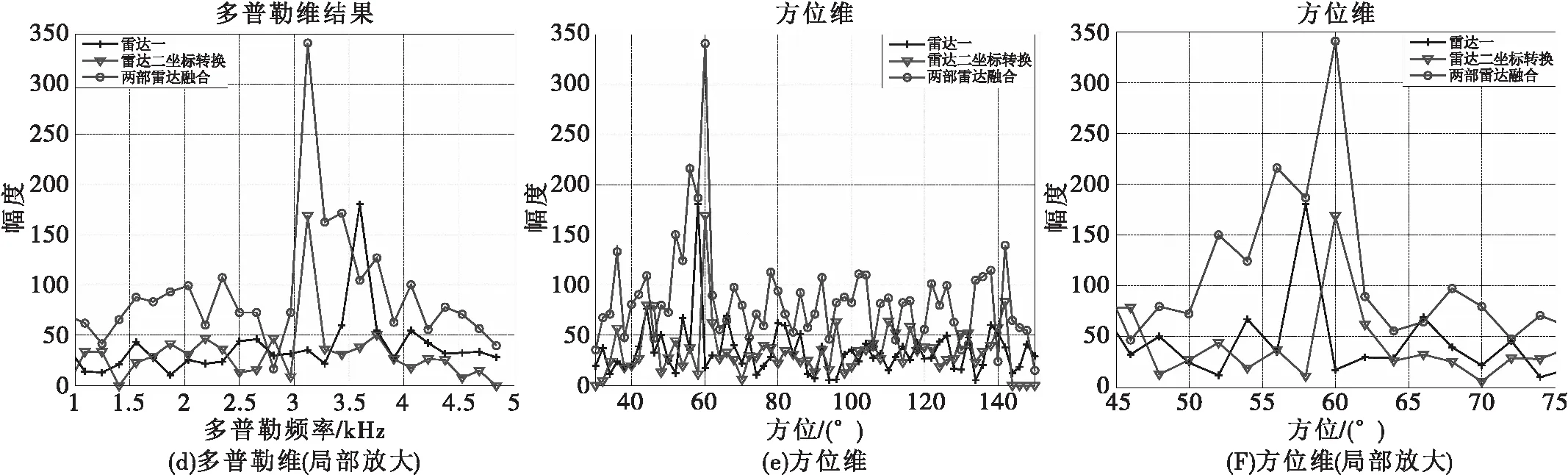
图7 信号级融合前与融合后结果对比图

3)两部雷达信号级融合算法检测性能仿真与分析。

下面通过蒙特卡罗试验研究两部雷达信号级非相参融合检测性能的改善，并通过理论分析进一步得到多部雷达进行信号级非相参融合的积累增益。

图8为通过蒙特卡罗试验得到的雷达一、雷达二及雷达一和雷达二进行信号级融合后不同信噪比下的检测概率曲线。由于雷达一和雷达二设置的仿真参数完成一致，因此雷达一和雷达二单部雷达的检测概率是一致的。从图中可以看出雷达一和雷达二经信号级融合后，与单部雷达相比，信噪比提高大约为2.5dB。图9为利用3.1节中Albersheim公式分析得到的不同积累样本下的非相参积累增益，从图8和9不难得到，对于两部雷达而言，蒙特卡罗试验结果与理论分析结果基本一致，从而验证了算法的正确性。从图9可以进一步得到多部雷达进行信号级非相参融合目标检测性能的提升能力；同时不难看出随着非相参积累样本的增加，积累增益会逐渐减小，显然对于略高于噪底的弱小目标通过多部雷达非相参融合来实现目标检测还十分困难，因此如何实现多部雷达的相参融合以更好的提升对弱小目标的探测性能仍需进一步研究。

图8 单部雷达与两部雷达信号级融合后检测性能曲线(Pfa=10-4)

图9 使用Albersheim公式计算非起伏目标的非相参积累增益(Pfa=10-4)

4)不同匹配误差下两部雷达信号级融合算法检测性能仿真与分析。

图10为在不同的距离方位匹配误差条件下两部雷达信号级融合后检测性能损失曲线。由于站址误差、空间坐标转换误差等多种误差的影响，空间坐标转换后只能实现近似配准，而且配准误差会随着站址误差、时间定位误差等误差的增大而增大。从图10中可以看出，该算法随着匹配误差的增加检测性能下降并不十分明显，这说明该算法具有一定的稳健性，同时不难发现，当匹配误差很大时，与单部雷达检测相比，检测性能提高十分有限。因此，采用多种措施减小各种误差的影响将有利于提高信号级融合后的检测性能。

图10 不同匹配误差下两部雷达信号级融合后检测性能损失曲线

从以上仿真结果可以看出，基于动态规划的信号级融合算法可以有效实现两部雷达信号级融合，并且具有一定的稳健性，验证了该算法理论的正确

性，同时在不考虑站址误差及时间误差的条件下，两部雷达进行信号级非相参融合信噪比可以提高大约2.5dB。

5)实测数据结果与分析。

本试验通过雷达对四旋翼无人机(如图11所示)进行照射，数据采样仪采样雷达回波中频信号，然后将采样的雷达回波数据在计算机上进行离线处理，以验证信号级融合相关指标。

图11 无人机飞行试验

雷达发射线性调频脉冲信号，时宽2μs，带宽40MHz，中频120MHz，脉冲重复周期200μs，数据采集仪采样率160MHz。

图12中的(a)、(b)、(c)展示了信号融合前和融合后距离维的结果，从图中可以看出，经空间坐标变换后，虽然距离维没有实现同一坐标系下的完全对齐，但是利用基于动态规划的信号级融合算法仍然实现了两部雷达的信号级融合，从而说明该算法的鲁棒性。

图12 两部雷达信号级融合前与融合后结果对比图

5 结束语

本文提出了一种基于动态规划的多站雷达协同探测信号级融合算法，目的是将各站雷达多普勒滤波后的数据经空间坐标转换后直接进行非相参融合，从而克服以前算法进行数据级融合信息利用不充分和不利于微弱目标检测的缺点。仿真表明，该算法不仅可以有效提高目标的检测概率，而且可以在误差条件下实现信号级融合；与此同时，通过实测数据验证了算法的可行性。该算法虽然提高了目标的检测能力，但是如何实现多部雷达的相参融合以更好地提升对弱小目标的探测性能并将该算法更好地应用到工程实践中尚需进一步的研究。