怎样引导数学解题反思

李寒月

摘要：反思就是个体对自己所想、所说、所做的动机、过程、结果进行再思考，从中总结得与失、经验与教训，获得感悟的过程。以一道简单的平面几何题为例，聚焦数学解题教学中的反思。教师可以引导学生从结论成立需要满足的条件、条件成立可以得到的结论、一题多变、一题多解等方面展开反思，以获得比较全面、深刻的认识。

关键词：数学解题教学;反思;平面几何题;基本图形

反思，就是回头看、回头想的意思，具体来说，是个体对自己所想、所说、所做的动机、过程、结果进行再思考，从中总结得与失、经验与教训，获得感悟的过程。从现代心理学的角度来看，反思是一种元认知——对认知的认知。反思，可以让我们获得更全面、更深刻的认识。

当然，学生的反思要想做到全面、深刻，离不开教师的引导。本文以一道简单的平面几何题为例，聚焦数学解题教学中的反思。

八年级学习“全等三角形”时，学生会遇到这样的基本问题：如图1，已知AB=CD，∠B=∠C，求证△AOB≌△DOC。其证明过程如下：因为AB=CD，∠B=∠C，∠AOB=∠DOC（对顶角相等），根据“AAS”，可得△AOB≌△DOC。

对于这道题的解决过程，教师可以引导学生从四个方面展开反思。

反思之一：结论成立需要满足什么条件

这道题主要研究两个三角形全等的关系。从结论成立需要满足的条件入手，可以引导学生反思：判定两个三角形全等有哪些方法？进而反思：满足哪些条件还能使这两个三角形全等？对此，学生不难想到，因为题目中已经有一个隐含的条件∠AOB=∠DOC（对顶角相等），所以只要再添加两个条件就能使这两个三角形全等。比如，添加AB=CD，∠A=∠D，根据“AAS”，可以得出△AOB≌△DOC;添加OA=OD，OB=OC，根据“SAS”，也能得出△AOB≌△DOC;添加OA=OD，∠A=∠D或添加OB=OC，∠B=∠C，都可以根据“ASA”，得到△AOB≌△DOC。

通过上述反思，学生不仅回顾了全等三角形的判定方法，还进一步尝试了从不同的角度得到两个三角形全等，从而加深了对全等三角形判定方法的理解。可见，从结论出发，思考结论成立需要满足的条件，是引导学生展开解题反思的有效途径。

反思之二：条件成立可以得到什么结论

显然，这道题根据已知条件，只能得出△AOB≌△DOC及对应的边和角相等的结论。其原因是图1比较简单，包含的元素比较少。由此，可以引导学生反思：怎样不改变题目的条件，而增加图中的元素，以得到更多的结论？对此，可以引导学生注意图1中有5个点，其中任意两点之间的连线还缺少AD和BC，从而想到把AD和BC分别连接起来（如图2）。这时，可以引导学生进一步反思：这样能得到哪些新的结论？比如：有没有新增的三角形？它们是否全等？全等的理由是什么？有没有特殊的三角形？有没有相等或平行的边？有没有相等的角？……通过对这一系列问题的思考，学生可以进一步得出△ABC≌△DCB，△BAD≌△CDA，△BOC、△AOD是等腰三角形，AD∥BC等结论。

虽然只是在图1的基础上添加了两条线段，但是衍生出了一系列新的结论。在研究上述问题的过程中，学生对这个图形和原来的问题就有了更全面、深刻的认识。可见，从条件出发，思考条件成立可以得到的结论，也是引导学生展开解题反思的有效途径。

当然，对于图1，除了考虑所有点都连线，还可以引导学生考虑所有线都“交”点，从而得到最“完备”的图形（如图3）。由此，可以引导学生进一步反思又能得到哪些新的结论……

反思之三：题目还可以怎么变化

对一个问题有了比较全面、深刻的认识后，就要引导学生反思这个问题可以发生怎样的变化：条件和结论都要改变。

教师可以继续引导学生观察图3，发现它是轴对称图形，比较“正”，从而想到让它“歪”一点。由此，可以引导学生思考：怎样“歪”才是基于原有图形自然生长的变化？进而引导学生发现，整个图形是由A、B、C、D四点决定的，而且，这四点具有一定的对称性，从而想到延长或缩短BD（或CA）。这样，随着点D（或A）的位置变化，点E的位置也跟着变化，整个图形就“歪”了。实际作图后，学生可以发现，这时，除了△BOC是等腰三角形及相应的边和角相等的结论显然还成立（不变），其他结论基本上都不成立（变）了。可以继续引导学生思考：在图形变化的过程中，有什么“不显然”的不变吗？如果有的话，便可以得到一个不错（有一定思维含量）的新题目。学生可以发现，如果∠BDC>90°，那么在延长BD（点D运动）的过程中，有一个点D的位置，使CD的长不变;如果∠BDC<90°，那么在缩短BD（点D运动）的过程中，有一个点D的位置，使CD的长不变。而在原有图形中，AB=CD。由此，在图形变化的基础上，可以让学生以AB=CD为结论命制一个新题目。接下来需要学生思考的问题便是：这个新题目的条件是什么？也就是说，在图形变化的基础上，满足什么条件可以得到AB=CD的结论？

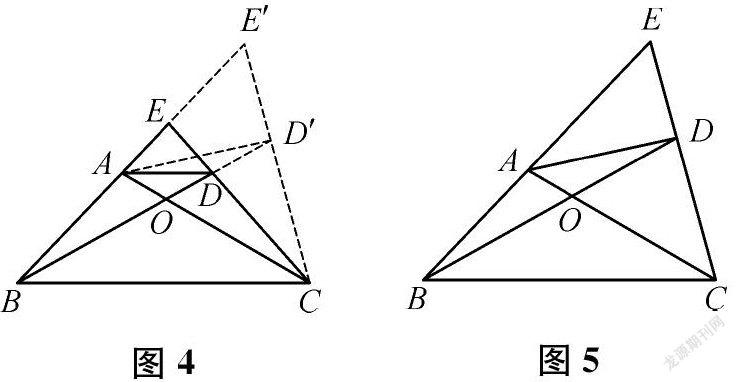
对此，可以∠BDC>90°，延长BD为例，将图形ABCDE变为ABCD′E′（如下页图4），引导学生发现：要使AB=CD′，只要CD=CD′，只要∠CDD′=∠CD′D;而∠CDD′=∠DOC+∠DCO，∠CD′D=∠E′+∠ABO，且∠DCO=∠ABO，因此只要∠DOC=∠E′;∠DOC=∠OBC+∠OCB，且∠OBC=∠OCB，所以只要∠OBC=∠OCB=1/2∠E′。

经过这么长的推理链后，只考虑变化后的图形，不考虑原有图形，学生便可得到这样一个不错的新题目：

如图5，在△EBC中，点A、D分别在EB、EC上，连接BD、CA，相交于点O，∠OBC=∠OCB=1/2∠E，证明：AB=CD。

在知道命题过程的情况下，解这道题十分容易。但是，如果不知道命题过程，要解这道题就比较困难了。由此，可以引导学生体会基本图形的作用。观察图5，会发现它和图3这个基本图形“长得很像”，只是“歪”了一点。注意∠OBC=∠OCB的条件，不难想到在OD上截取OD′=OA或在OA延长线上截取OA′=OD，从而构造基本图形（如图6或图7）。由此，很容易得到AB=CD′或A′B=CD。接下来便可以用分析法证明CD′= CD或A′B= AB。证明过程基本上就是上述命题过程，这里不再赘述。

反思之四：题目还有什么解法

上述新題目比较复杂，教师可以引导学生思考它有没有更多的解法（过于简单的问题通常没有很多有价值的解法），进而寻找解法之间的联系，以发现问题的本质、解法的核心。

为此，需要引导学生反思已有的解法，发现其关键是构造基本图形，而构造基本图形的目的是得到全等三角形。可以进一步引导学生，分析发现，上述解法中构造全等三角形的思路是，保持一个（组）三角形不变，改变另一个（组）三角形的形状和大小。由此，学生可以想到：能否同时改变两个（组）三角形，从而构造全等三角形？于是，解决问题的思路再次打开，得到一些新的解法：

新解法1：如图8，过点C作CG⊥BD于点G，过点B作BF⊥CA于点F，根据基本图形，很容易证明△BFC≌△CGB（AAS），再证明△BFA≌△CGD（AAS），从而得出BA=CD。

新解法2：如图9，延长BD至点G，延长CA至点F，使BF=BO，CG=CO，则可以得到△BFO≌△CGO（AAS），进而得到△BFA≌△COD（AAS），从而得出BA=CD。

而且，学生不难发现，此题的解法不限于此，还有很多。这时，可以引导学生反思：这些解法之间有无联系？通过对比，学生可以发现，这些解法的本质都是构造基本图形，获得全等三角形（图8、图9中的四边形FBCG其实也是基本图形——图2）;不同的解法只是添加的辅助线不同，构造的基本图形有变化。由此，可以引导学生充分体会基本问题（图形）思想：把一些基本问题（图形）吃透后，遇到复杂问题（图形）时，往往可以通过分解、演变得到基本问题（图形），从而找到解题思路和方法。