EGM2008模型在山区GNSS高程转换中的应用分析

宋 宁，龚真春，王积武，白 冰，吴 洋

（61287部队,甘肃 兰州 730020）

采用传统的水准、三角高程测量方式在山区、荒漠等地区进行控制点高程测量时，精度虽然高，但实施难度大、效率低。利用全球导航卫星系统GNSS定位技术可快速、精确地测定出点位cm级甚至mm级的三维坐标，但其测定的是大地高，不是我国所采用的正常高，因此需要对二者进行高程转换。目前，在测量作业中普遍通过GNSS/水准拟合方法来获取点位的正常高，但需要测区内有一定数量的已知水准点、分布均匀且覆盖测区，这对水准点稀少的地区，会有诸多的不便。

近年来，国内众多学者就EGM2008地球重力场模型实现GNSS高程转换进行了大量研究，并成功应用于工程实践中[1]。利用GNSS和EGM2008模型进行跨海高程传递，200km范围内高程精度优于10cm，10km范围内可达6cm的结果；文献[2]将EGM2008重力场模型应用于无验潮测深，坐标转换误差和测深精度均达到cm级。本文针对山区地形复杂、已知水准点少、常规高程测量方法实施困难等实际，探讨直接使用EGM2008地球重力场模型求取点位高程异常，然后采用差分抵消高程基准系统偏差的方法求取点位正常高，并以实例数据进行对比分析。

1 EGM2008模型简述

EGM2008地球重力场模型是美国国家地理空间情报局（NGA）于2008年推出的新一代地球重力场模型。模型提供的最终成果包括：2190阶次的全球重力场模型；全球5′×5′空间分辨率的重力异常；全球 5'×5'、2.5'×2.5'、1'×1'网格大地水准面；全球 5'×5'网格垂线偏差[3]。

高程异常是地球重力场的主要参数之一，根据Bruns公式可求得地面上任意一点A的模型高程异常[4]。

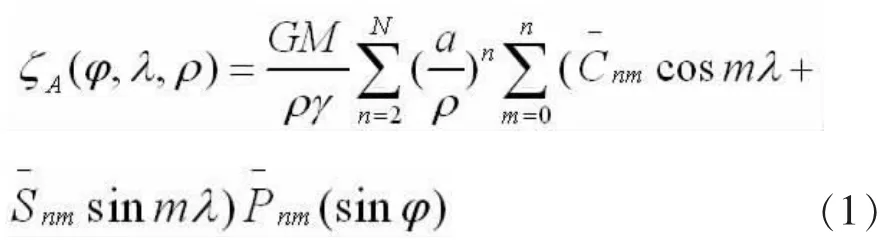
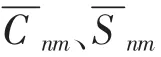
对于EGM2008模型在我国大陆地区的精度以及适用性问题，国内很多学者都进行了深入的研究。章传银等[5]利用我国大陆GPS水准实测高程异常，对EGM2008模型在我国大陆地区的精度以及适用性问题进行了研究，得出EGM2008模型高程异常在我国大陆的总体精度为20cm，但表现出区域不均衡性，华北地区9cm，华东华中地区12cm，西部地区为24cm。

2 GNSS高程转换基本原理与方法

GNSS技术测定的大地高同我国采用的正常高之间的关系为：

由式（2）可知，GNSS高程转换的关键在于高程异常的求解。现阶段主要有物理重力法和几何拟合法，物理重力法需要地球重力模型、重力数据，用式（1）计算出点位高程异常，按式（2）求得点位的正常高，由于受成本、资料保密等多种因素的制约，实际应用较少，EGM2008地球模型及其他模型的公开发布，使这一问题得到了较好地解决。几何拟合法是指利用测区内一定数量的GNSS/水准重合点位，通过已知高程异常值构建测区似大地水准面，再由数学方法求解区域内任意一点的高程异常值，拟合法容易实现、方法较多，这里不再详述。

由于我国的高程基准与EGM2008模型所定义的全球似大地水准面之间存在着一个系统偏差△H0，若直接利用EGM2008模型进行GNSS高程转换时，效果不理想[6]。因此，可将式（2）表达为：

根据高程异常曲面同样均衡性特点，模型误差具有较强的相关性，这种系统误差△H0可通过差分被抵消。设地面任意两点 和之间的正常高的高差△hij为：

结合式（3）可知：

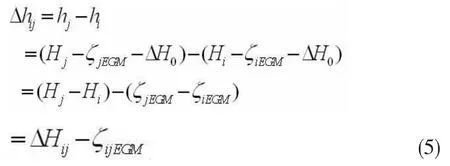
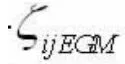
若在测区范围内有1个已知GNSS/水准点，其正常高为hp，则由式（4）、式（5）可得未知点 hi的正常高为：

3 算例分析

采用文献[8]中的17个已知GNSS控制点进行验证分析，控制点分布如图1所示。

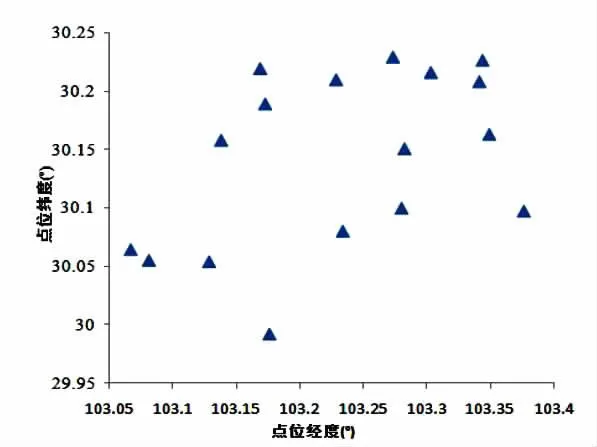
图1 已知控制点分布情况

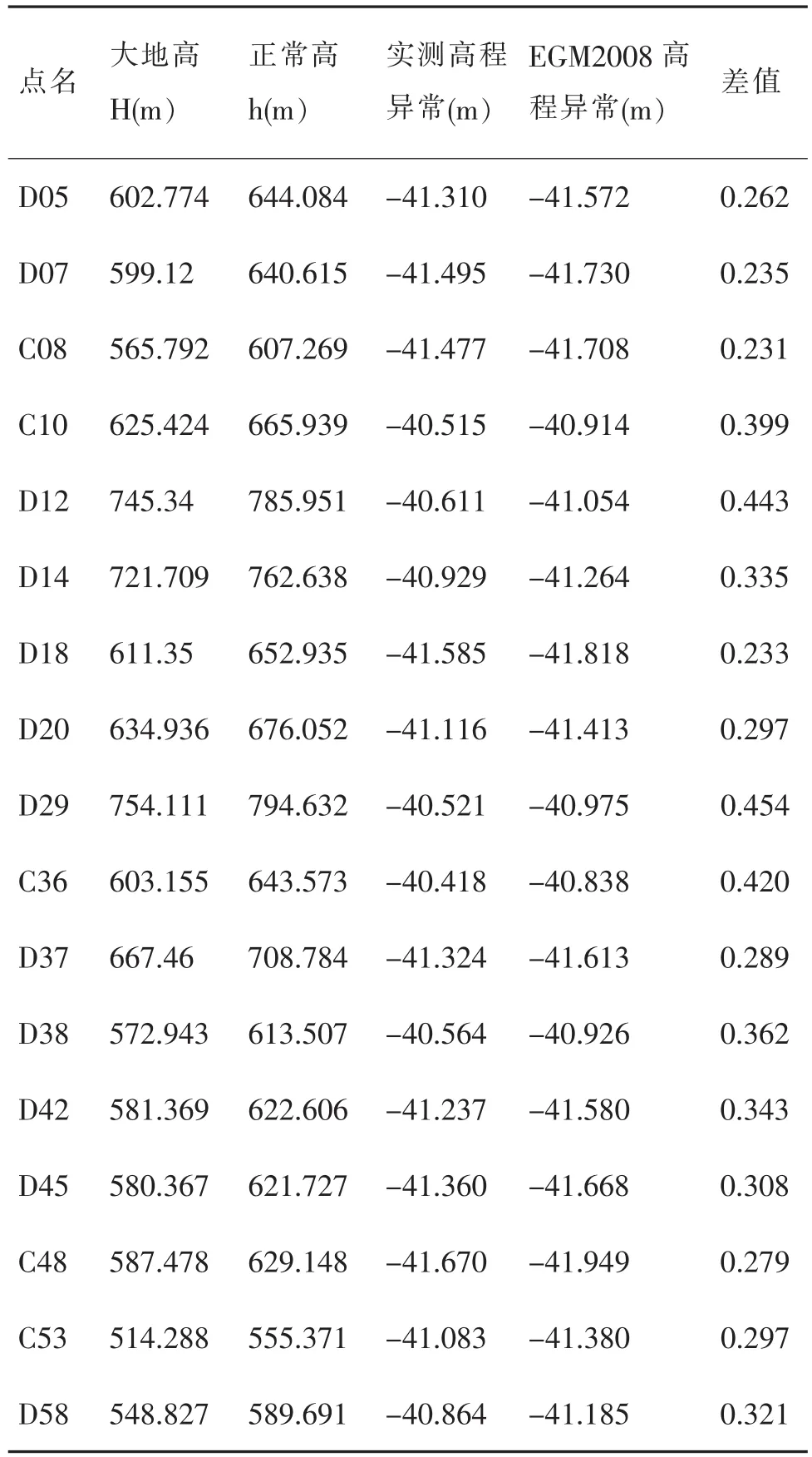
实例中的17个GNSS控制点均进行了四等水准测量。为方便后续对比分析，利用EGM2008计算软件“Alltrans EGM2008 Calculator1.2”得到点位高程异常。17个已知控制点数据整理见表1。

为验证本文差分抵消高程基准系统偏差求取点位正常高方法的可行性及精度。现分以下三种方案进行比较分析。

1）方案一：假定测区内无利用的已知水准点，直接由GNSS测定的大地高、EGM2008模型计算出的高程异常，按式（2）求取正常高。同已知正常高比较结果如图2所示。由表1、图2可知，直接利用大地高、EGM2008模型求出的点位正常高，系统偏差为0.324m，正常高最大相差为0.454m、最小0.231m，中误差为0.331m，效果不理想。

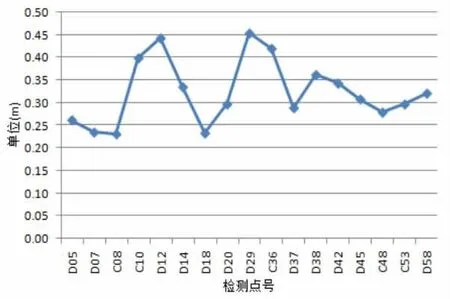
图2 直接利用EGM2008模型求取的正常高差值

2）方案二：以常用的GNSS/水准平面拟合的方法，选取3个已知点C08、C36、D45求出拟合参数后，计算得到其余14个点的正常高，同已知正常高进行比较，其差值统计如图3所示。其中，正常高最大相差为0.159m、最小0.003m，中误差为0.086m。同方案1相比，整体精度有了较大提高。

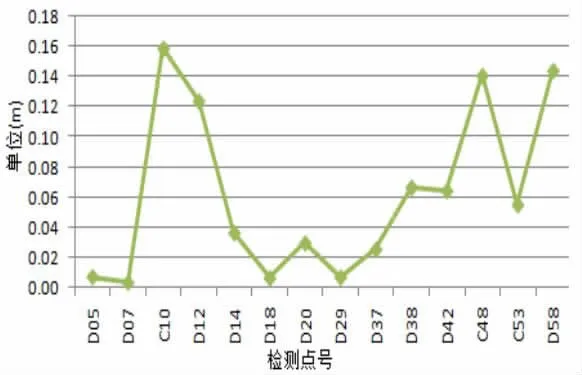
图3 平面拟合方法求出的正常高差值

3）方案三：按本文所提出的方法，在测区内选取1个已知点D05，根据式（6）计算出其余16个点位的正常高，同已知正常高进行比较，其差值统计如图4所示。其中，正常高最大相差为0.192m、最小0.017m，中误差为0.096m。同方案1相比，整体精度同样有了很大的提高；同方案2相比，精度基本相当。

三种方案求解出的点位正常高同已知正常高的差值统计如图5所示。

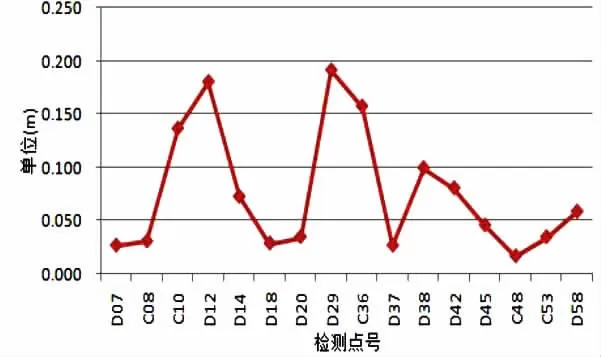
图4 经差分抵消基准系统偏差后的差值

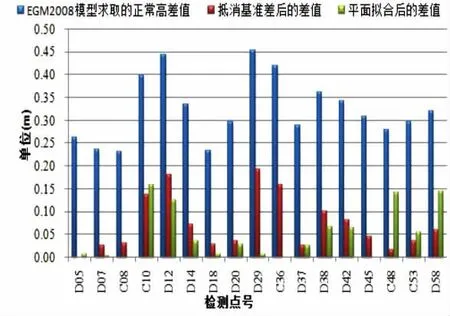
图5 三种方案正常高差值统计

综合上述各方案和图5可得出：在不进行水准或三角高程联测的情况下，方案二、方案三完全满足1:5000比例尺成图及一般工程作业精度要求。但在方案二中只利用1个已知水准点，在水准点稀少的困难地区作业时，更具有实用价值。

4 结语

本文探讨利用EGM2008重力场模型获取点位正常高的方法，对于已知水准点少、测区联测困难、交通不便等实施常规高程测量困难的测区有较强的现实意义。