基于组合赋权的TOPSIS方法的甘肃省祁连山东段草地生态安全评价＊——以甘肃省天祝藏族自治县为例

牛雪娜，史战红，周生伟，朱亚莉

（甘肃农业大学 理学院 数量生物学研究中心，甘肃 兰州 730070）

1 概述

草地既是区域生态环境最基本和最主要的构成要素，也是当地社会经济发展的主要依托，草地资源对当地的生态环境和社会经济发展具有决定性的影响。草地生态环境的破坏以及草地的严重退化是全球面临的主要生态问题之一，目前许多国家和地区都面临着草地生态系统退化所造成的生态和贫困等问题的困扰[1]。本文以甘肃省天祝地区的草地生态系统作为研究对象，该区域地处甘肃省祁连山东段的高寒牧区，是典型的生态脆弱区，近些年随着人口及牲畜数量的不断增长，严重地导致天然草地退化，并由此引发了水土流失、生物多样性地大幅减少、土壤急速退化等一系列生态环境问题，已经严重威胁了当地区域的草地生态安全。2016年，张强等[2]采用可拓综合分析方法建立了能够反映祁连山生态功能区安全的评价模型。2017年，王治和等[3]以祁连山冰川与水源涵养生态功能区张掖段2005～2015年的数据定量评估了该区域的生态安全，并对2017年该区域的生态安全环境进行了动态预警。

综上，学术界对祁连山生态评价的显著特点是以生态承载力、区域生态安全和草地生态系统服务功能价值研究为主，向我们展现了不同的理论指向。然而，文献中很少有探讨甘肃祁连山东段草地生态安全评价的相关研究。本文拟在借鉴、反思以上研究成果的基础上，立足于草地生态系统的功能和作用，在草地的可持续利用理论基础和技术的指导下，选择祁连山东段的草地生态系统作为研究对象，对其安全性做出合理的评价。

2 研究方法

2.1 层次分析法

每一项指标在指标体系中的重要性不同，在实际问题中往往引入权重来表示其差异性。当指标体系的指标较多且具有分层结构时，尝试使用层次分析法来确定各指标的权重。该方法由美国运筹学家Saaty[4]所提出，它是一种定量与定性相结合的多目标决策分析方法，现将其分为以下四个步骤进行：

1）构建指标层次结构（如图1所示）。

2）由专家给出的意见，再结合Saaty给出的1-9标度法（见表1）并将其定量化。以期构造反映各指标间重要性程度的判断（成对比较）矩阵。

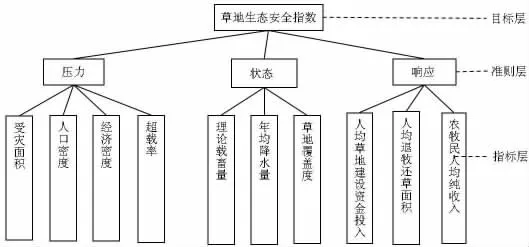
图1 指标层次结构

表1 1-9标度法

3）求解第2步判断矩阵的最大特征值λmax及其对应的归一化特征向量，将此向量作为本层的指标对应于上一层指标的权重，由此完成层次单排序。并由CI和CR进行一致性检验：

（1）式中，CR为判断矩阵的随机一致性比率；CI为判断矩阵的一致性指标且

RI为判断矩阵的平均随机一致性指标，部分阶的判断矩阵的值见表2。

表2 平均随机一致性指标值

当判断矩阵的时CR<0.1，认为判断矩阵具有满意的一致性，否则要调整矩阵中的元素使其具有满意的一致性。

4）根据分层指标间的层级关系，求出最底层指标相对于目标层的权重，完成层次总排序，并作相应的一致性检验。

假定已知层次所有B的因素B1，B2…，Bn的权重值（总排序结果）分别为 b1,b2,b3…,bn。 bj对应本层次 C 中因素 C1，…，CP单排序的结果为 Cj1，…Cjn，所得层次总排序见表3。

表3 层次总排序

层次排序是自上而下逐层进行的，其结果按公式（2）进行一致性检验。

2.2 最大熵权法

在多指标的决策问题中，最大熵权法可以确定各评价指标的权重[5]。它的基本原理是：从个方案中选取最优方案，这取决于个方案的各个指标向决策者所提供的信息，如果在决策表中提供的确定信息量大者，那么该信息量对决策做的贡献就大，从而所对应的指标权重值也就越大。

第一步：假设多指标决策问题有n个指标G1，G2，…，Gn，m 个可行方案 A1，A2，…Am，其决策矩阵 D 为

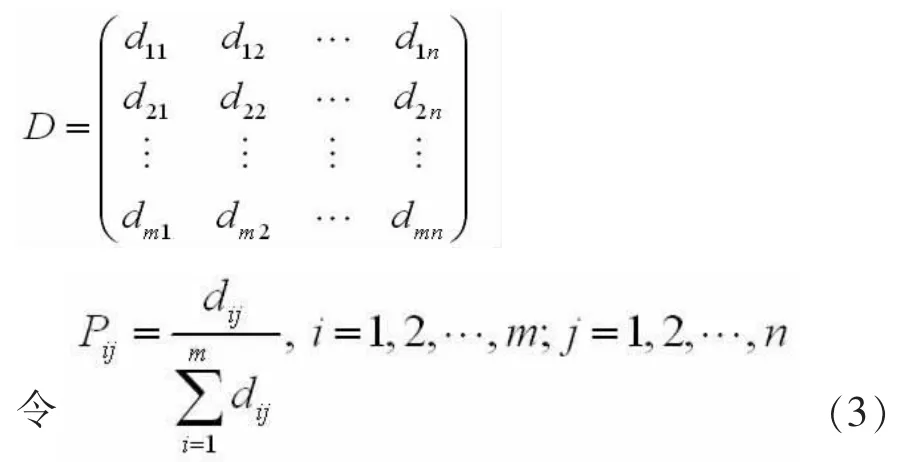
则第j个指标的输出熵为

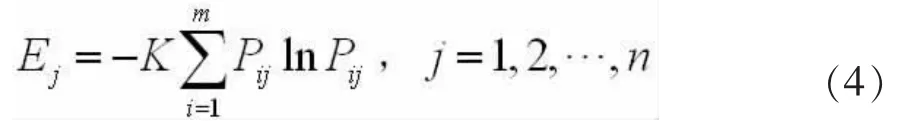
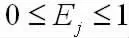
第二步：若决策者对n个指标G1G2，…Gn无明显的偏好，即认为这n个指标重要程度相当，则指标Gj的权重Wj为

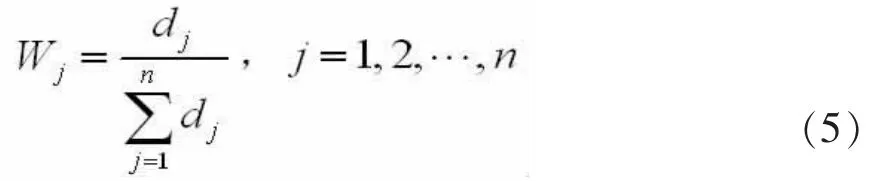
2.3 TOPSIS法

TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution）法简称为逼近理想点法，此方法是Hwang和Yoon[6]于1981年提出的，是一种解决多指标决策问题的行之有效的方法。为了得到可行方案的优劣排序，将此方法分为五个步骤进行。

1）将决策矩阵 D=（dij）m×n标准化。即

2）计算加权标准化决策矩阵 V=（Vij）m×n。

由层次分析法和最大熵权法组合赋权求出了评价指标权重 W=（W1，W2，Wn），则加权标准化决策矩阵为

3）求正理想方案和负理想方案。

则 A+=（V+1，V+2，V+n）为正理想方案，A-=（V-1，V-2，V-n）为负理想方案。

4）计算各可行方案到理想方案的距离

Ai到正理想方案A+的距离为

Ai到负理想方案A-的距离为

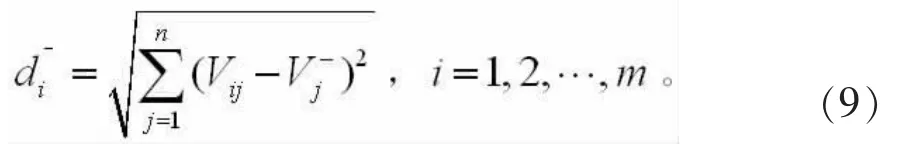
5）计算各可行方案到理想方案的相对接近程度

Ai到理想方案的接近程度为

最后，由Ci的大小来确定方案的优劣。即当Ci越大，对应的方案Ai越优。

3 指标权重的确定

层次分析法得到的权重体现了决策者的意向，具有较大的主观随意性。最大熵权法是采用相关的数学理论结合数据计算出的权重，但该方法没有考虑决策者的主观意向。为了使得权重更为准确、更为合理，采用主观与客观相结合的权重设置方法，即层次分析法与最大熵权法组合对指标进行赋权。

3.1 利用层次分析法确定权重

为了体现草地生态的系统性和安全性，结合草地生态安全评价的相关理论及指标选取准则，采用层次分析法建立三个层次的草地生态安全评价指标体系。以草地生态安全指数作为目标层；以压力、状态和响应作为准则层去刻画目标层；由表达每一个相应准则的具体指标作为指标层，以此构建出草地生态安全评价的指标体系，见表4。

表4 草地生态安全评价指标体系

首先构造准则层两两比较的判断矩阵，以确定各准则对目标层的权重。该矩阵的元素bij是由Saaty的1-9标度法结合草地生态相关理论给出，即O-B层判断矩阵如下。

使用MATLAB软件计算出上述判断矩阵的最大特征值为

λmax=3.0183

对应的归一化特征向量为

wB=（0.6250,0.1365,0.2385）T

判断矩阵的随机一致性比率CR为

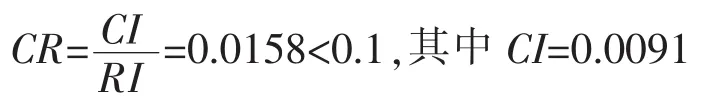
因此，认为此判断矩阵具有满意的一致性。

用同样的方法计算出指标层中每个指标相对于其上一级准则的判断矩阵分别如下所示。

B1-C层

B2-C层

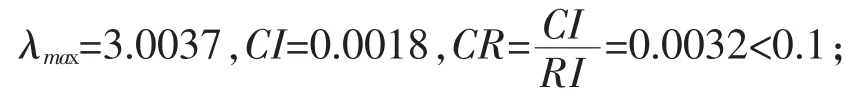
B3-C层

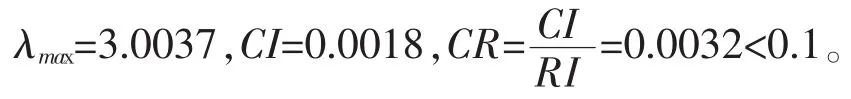
最后，由表3的层次总排序得到10个指标的权重，见表5。

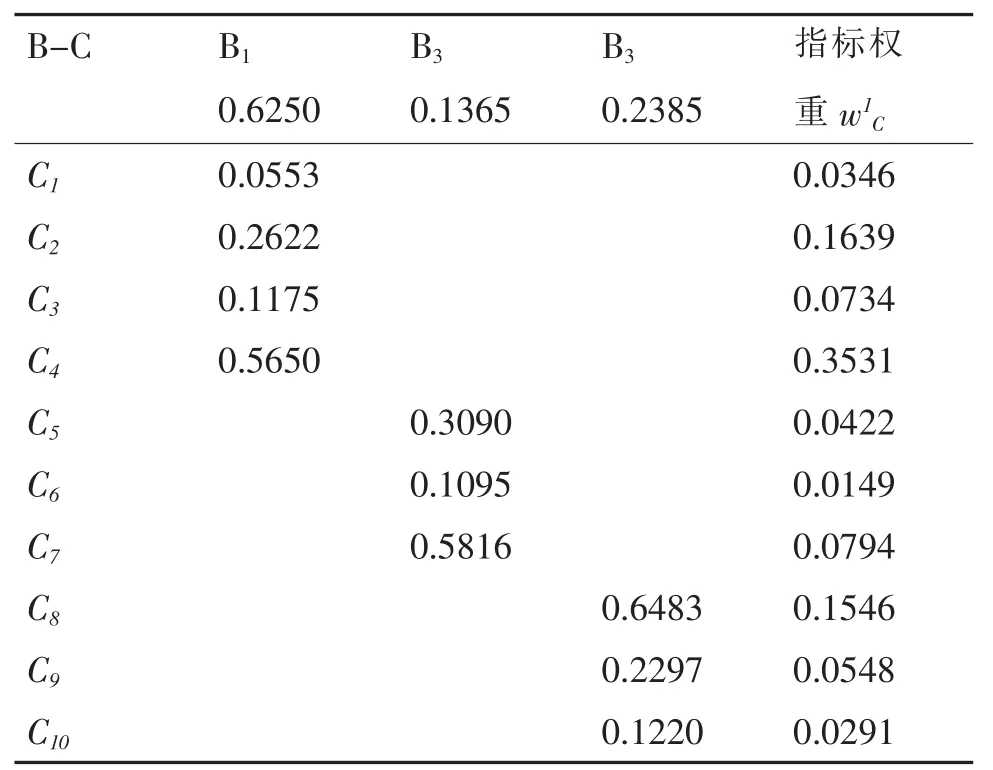
表5 指标层权重

总排序的一致性检验：

因此，总排序具有满意的一致性。即通过层次分析法得到权重为：

w1C=（0.0346,0.1639,0.0734,0.3531,0.0422,0.0149,0.0794,0.1546,0.0548,0.0291）T

3.2 利用最大熵权法确定权重

以受灾面积、人口密度、经济密度、超载率等10个指标作为评价指标，由公式（3）、（4）和（5），得到这10个指标的权重为：

w2C=（0.2109,0.0784,0.0716,0.0002,0.0848,0.2021,0.06820.0.0874）T。

经由组合赋权即公式（6）可得权重为：

4 基于TOPSIS模型的构建

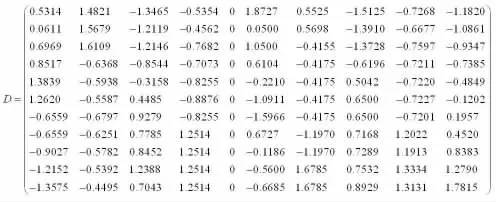
以2007-2017年的受灾面积、人口密度、经济密度、超载率等10个指标值的数据，由公式（7）得到标准化的决策矩阵D：

建立多属性决策模型：

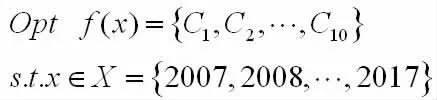
应用TOPSIS法步骤3至步骤5进行多属性决策，对甘肃省祁连山东段2007-2017年的草地生态安全优选和排序，得到草地生态安全指数为：

C=（0.3381,0.2772,0.3563,0.3811,0.4399,0.4356,0.2113,0.6274,0.5974,0.5852,0.5667）T

由图2可知，甘肃省祁连山东段2007年至2017年的草地生态安全指数总体呈现出上升的趋势，在总体上升的同时，个别年份又有所下降。其中，2007年、2008年和2013年草地生态安全指数均小于0.35[7]，草地生态安全的状况较差；2009-2012年草地生态安全指数在0.35～0.45之间，草地生态安全的状况一般；2013年草地生态安全指数大幅度下降为0.2113，安全状况变得较差，而从2014年开始又有显著的上升，草地生态安全指数均大于0.45，安全状况良好，最后基本呈现稳定。

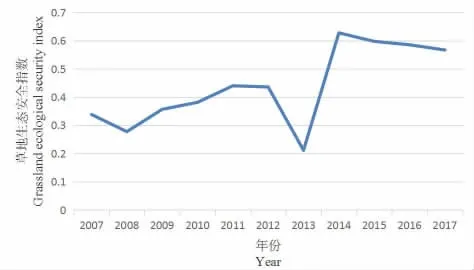
图2 甘肃省祁连山东段草地生态安全指数

5 结论

以常用的衡量草地生态安全的三个准则：压力、状态和响应出发，结合评价指标体系构建的层次性原则，建立评价草地生态安全的指标体系。由于草地生态安全的评价涉及多个年份的多准则及多属性问题，在此采用TOPSIS法对草地生态安全进行评价。甘肃省祁连山东段2007年至2017年的草地生态安全指数总体呈现上升的趋势，这也是近年来对牧民实施禁牧和轮牧、天然草地进行围栏封育和施肥灌溉；同时对草地退化较严重的区域采取以播种优良牧草为主的综合培育方式[8]，当地政府对于天然草地实施的一系列保护措施取得了显著成效。草地生态安全指数总体呈上升的趋势，2007年、2008年和2013年草地生态的安全状况较差，其主要原因可能还是牧民地过度放牧所致。草地生态安全指数在2013年出现大幅度下降，安全状况较差，其原因可能是对于草地退化较严重区域所播种的优良牧草成活率有所下降且毒草生长的速度过快所致[9],但在2013年至2014年草地生态安全指数有了显著地上升，安全状况较好，最后基本呈现稳定。今后政府应继续实施天然草地的保护政策，对于禁牧期的牧民政府可以给予适当的补助，同时也要强化牧民的草地生态环境保护意识，以期促进祁连山东段草地生态恢复以及草地畜牧业的转型升级[10-11]。