关于d元广义Legendre-Sidelnikov序列的自相关性研究
申诗萌,刘华宁
(西北大学 数学学院,陕西 西安 710127)
具有良好伪随机性质的序列在通讯和密码学上起着重要的作用,其中很多具有这些特性的序列是基于有限域的乘法特征来构造的[1-8],包括Legendre序列、Sidelnikov序列和双素数序列。Su和Winterhof结合这3个序列的概念构造了一个新的Legendre-Sidelnikov序列[9],具体来说,设p是一个奇素数,q是一个奇素数幂且满足gcd(p,q-1)=1。令
m=p(q-1),
P={0,p, 2p,…,(q-2)p},
R={0,1,2,…,m-1}(P∪Q*),
Su和Winterhof研究了该序列的自相关性,给出了周期自相关的精确值和非周期自相关函数的一个上界, 并且注意到该序列仅在p=q时是平衡的[9]。文献[10]研究了k阶相关测度以及线性复杂度。此外, Su给出了该序列在不同条件下线性复杂度的上界和下界[11]。相关研究成果还可参考文献[12]和文献[13]。
χp(α)=ω,χp(0)=0,

χp(i)=χp(αj)=ωj,

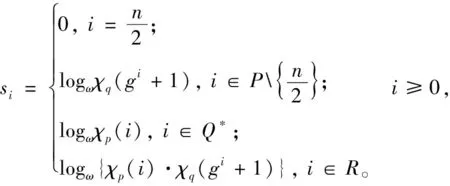
(1)

对于周期为T的d元序列(si),周期自相关函数的定义为
其中1≤l 本文对于一般的d,完全给出d元广义Legendre-Sidelnikov序列(1)的自相关值,主要结论见定理1。 定理1设(si)如序列(1)中的定义。则有 AC(si,l)= 证明见文献[14]中引理3。 证明见文献[14]引理4。 根据d元广义Legendre-Sidelnikov序列(1)的定义,有 (2) 下面,分3种情形证明定理1。 情形1当l∈P{0}时,该情况在文献[14]中得到了证明。 情形2当l∈Q*时,由式(2)得 ωsi-si+l= 因此 (3) 结合引理2,得到 (4) 以及 χp(-l)(-χq(-1)-1)。 (5) 再由引理1,可得 (6) -χq(2) (7) 以及 χq(-1)+1。 (8) 最后,结合式(3)至式(8)可直接得到 χq(2)χp(-l)+χp(-l)(-χq(-1)-1)- χq(2)+χq(-1)+1= 情形3当l∈R时, 由式(2)得 ωsi-si+l= 根据引理1,得到 (9) (10) -χq(-g-l+1)。 (11) 再结合引理2,有 (12) (13) 以及 (14) 当l满足(q-1)|l时,结合式(9)、式(12)至式(14),得到 (q-2)χp(-l)-(q-2)= 然而,当l∈R满足(q-1)不整除l时,有 χp(-l)χq(-g-l+1)+ χp(-l)χq(-g-l+1)+ χq(g-l)+1= 综上,即完成了定理1的证明。 在文献[14]中,Su利用乘法特征将一般的Legendre-Sidelnikov序列推广成形为序列(1)的d元平衡序列,其中d是p-1和q-1的一个公共因子,并且gcd(p,q-1)=1。而本文的主要结果是进一步计算了该d元广义Legendre-Sidelnikov序列的自相关值,并利用特征和的性质证明了该序列有很好的自相关性质,完整地解决了该序列自相关性的研究。1 关于特征和的一些引理


2 定理1的证明




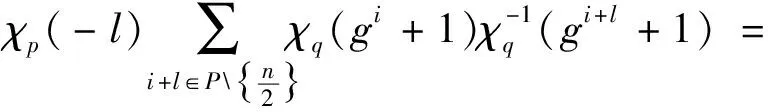
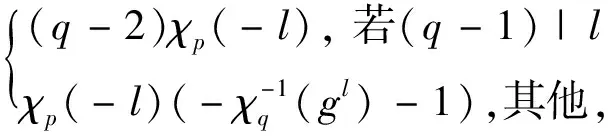

3 结语

