一种新的病态问题奇异值修正方法

杨秋伟,陈华,周聪,李翠红

(1.绍兴文理学院 土木工程系 浙江 绍兴 312000;2. 宁波工程学院 建筑与交通工程学院,浙江 宁波 315211;3. 浙江省土木工程工业化建造工程技术研究中心(宁波工程学院)，浙江 宁波 315211)

0 引 言

在测量平差问题中,最小二乘估计是求解线性方程组最常用的方法之一,例如,考虑一个常见的线性估计模型:

y=A·x,

(1)

式中：向量y为已知的观测向量(m×1维);A为系数矩阵(m×n维列满秩矩阵);向量x为未知的参数向量(n×1维).利用最小二乘法求解方程(1)的过程如下:

对方程(1)两边乘以AT,可得法方程为

z=B·x,

(2)

式中,B=ATA,z=ATy.由方程(2)可得x的最小二乘估计为:

xlse=B-1·z.

(3)

由方程(3)所得的最小二乘解满足最优线性无偏性,因此最小二乘估计又称为无偏估计.然而,当线性方程的系数矩阵A存在复共线性时,即A中某些列向量相关度很高时,由方程(3)所得的解可能误差很大甚至完全失真,这种情况称为病态最小二乘问题[1-5].为了得到准确的x估值,必须研究其他的稳健算法.

1 奇异值截断方法

如前所述,针对病态最小二乘问题,学者们已提出各种稳健估计算法.其中,奇异值截断方法[6-11]是最具代表性的一类方法.这类方法普适性强,既可适用于方程数目大于或等于未知量数目的情况(系数矩阵A列满秩),也可适用于方程数目小于未知量数目的情况(系数矩阵A行满秩),还可适用于系数矩阵为亏损矩阵的情况.其理论依据是,在方程组系数矩阵的所有非零奇异值中,较大的奇异值对数据噪声不敏感,而较小奇异值(接近于0的奇异值)体现了系数矩阵的复共线性,且对数据噪声很敏感.因此,在方程求解时忽略较小的奇异值而只保留较大的奇异值,相当于一定程度上消除了系数矩阵的复共线性,增强了抵抗数据噪声干扰的能力,从而可以获得比较稳定的计算结果.

利用奇异值截断方法求解线性方程组的过程简述如下.不失一般性,考虑一个任意的线性方程组如下：

y=C·x.

(4)

与方程(1)不同,方程(4)中的系数矩阵C对矩阵维数和是否满秩没有特殊要求.接下来首先对方程(4)中的系数矩阵C做奇异值分解,即

C=UΛVT,

(5)

U=[u1,u2,…],V=[v1,v2,…],

(6)

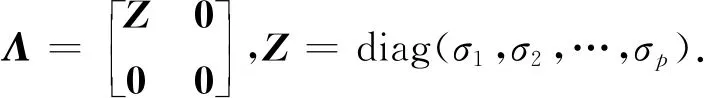
(7)

式中,σ1,σ2,…,σp为矩阵C的p个非零奇异值,且满足σ1≥σ2≥…≥σp.方程(5)代入方程(4)中可得x的解为

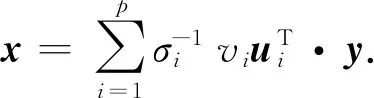
(8)

由方程(8)可见,越小的奇异值倒数越大,其微小变化将引起解的很大变化.因此,为了提高解的稳定性,在方程(8)中可以舍去较小的奇异值,而只保留较大的奇异值.假设只保留前t个奇异值,t又称为截断阈值,则截断奇异值后所得的解为

(9)

方程(9)即为奇异值截断方法计算x的公式.显然,决定该方法计算精度的关键是确定合适的截断阈值t.不少学者就此开展研究工作,代表性的方法有F检验法[10],广义交互确认法(GCV)[12],L曲线法[13]等.但这些方法均需要花费额外的计算量,操作步骤上比较复杂,且容易出现误判.

2 奇异值修正方法

鉴于奇异值截断阈值选择过程比较复杂,增加的额外计算量较多,有些学者提出了奇异值修正的方法[9,12-16],其核心思想是对较小的奇异值进行适量的修正(增大),从而使得结果更为稳定.这些奇异值修正方法所提的修正公式基本都是分段函数,比如文献[9]中所提修正公式为

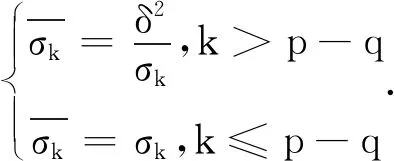
(10)

文献[14-16]中所用的修正公式为

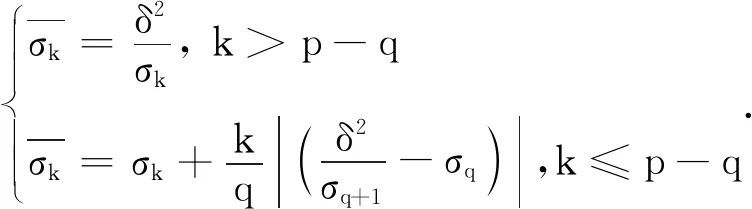
(11)

显然,这些修正公式中仍然需要确定一个修正阈值q,来对不同的奇异值选择相应的修正函数. 确定修正阈值q的计算量仍然与确定截断阈值t的计算量相当,在应用上仍然不太方便,尤其是对于大规模的线性方程组,计算过程很复杂.因此,本文提出一种新的奇异值修正公式,对所有的非零奇异值都采用同样的修正公式,形式如下

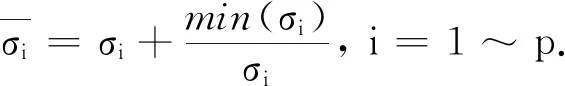
(12)

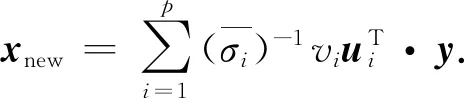
(13)

显然,采用本文所提的奇异值修正公式,并不需要确定任何阈值,基本没有增加额外的计算量,有利于工程应用.由后继的数值算例可见,本文方法可以获得比奇异值截断法精度更高的计算结果.

3 数值算例

3.1 病态平差模型

以文献[17]所用的病态平差模型y=A·x为例,验证所提的奇异值修正法,该方程的系数矩阵A和观测向量y的真值为

(14)

未知参数向量x的真值为

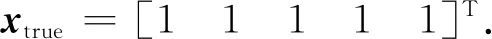
yc=[-10.178 1, 10.640 4, 1.372 4, 12.05, 13.607 7,-0.112 2, 20.942 2, 1.554, 9.328 6, 12.112 3]T.

采用本文所提奇异值修正法,即利用方程(12)和(13),所得的估值xnew的元素值列于表1中.另外,为了比较本文方法、最小二乘法和截断奇异值方法,表1中同时给出了最小二乘估计xlse的元素值和取最优截断阈值t=3时的x估值xt的元素值.为了评估这三种解与真值之间的接近程度,表1中还给出了各个估值与真值之差的2-范数eΔx.

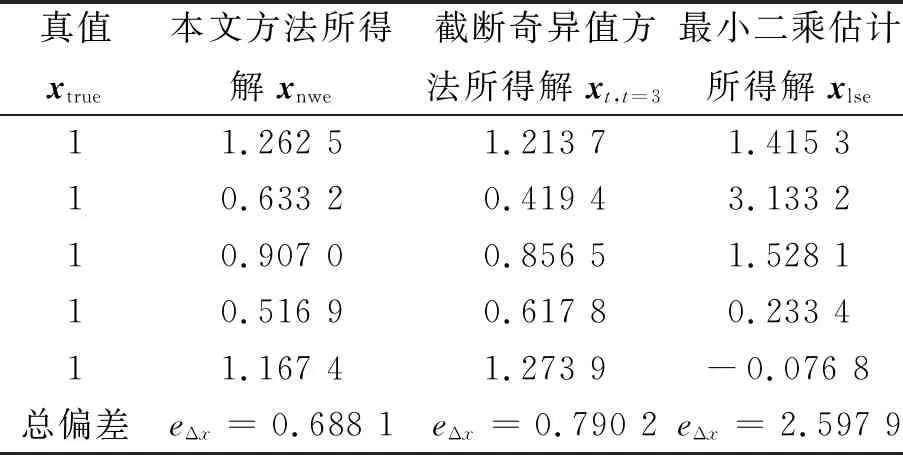
表1 本文方法与最小二乘估计和截断奇异值方法的比较

由表1可见,最小二乘估计xlse与真值差别很大,已完全失真.而采用本文所提奇异值修正方法,所得结果(xnew)的元素值要比奇异值截断法(xt)的元素值更准确,且本文方法计算公式十分简单快捷,并不需要任何额外的运算,方便工程应用.

3.2 Hilbert病态矩阵

Hilbert病态矩阵[18]经常用于测试各种稳健估计算法的可靠性,该矩阵由如下公式产生:

(15)

式中,i、j为该矩阵中元素hij的行号和列号.随着矩阵维数的增大,Hilbert矩阵的病态性也会越来越严重.以Hilbert矩阵为系数矩阵,建立线性方程如下:

Hm×n·x=y.

(16)

不失一般性,假设该方程中x的真值取为全部元素等于1的列向量,而观测向量y取为Hm×n·(1,1,…,1)T.现利用本文方法来对方程(16)进行求解,为了说明所提方法的普适性,考虑三种类型的Hilbert矩阵,分别为:行数大于列数、行数等于列数和行数小于列数,不失一般性,分别取系数矩阵为H30×20、H20×20和H15×20,利用本文方法的计算结果xnew的元素值列于表2中.另外,为了便于比较,表2中也给出了部分最小二乘估计和奇异值截断解.

由表2的第2和3列可见,系数矩阵取为H30×20时(行数大于列数),即使方程中不含有数据噪声,用最小二乘法计算的结果xlse的元素值也是完全失真的,因为系数矩阵的病态性相当严重,而采用本文方法所得结果与真值高度一致.因此,对于病态非常严重的方程组,最小二乘法已完全不能使用,故对于系数矩阵取H20×20和H15×20的情况不再给出最小二乘解.对于后两种情况,表2的第4和6列分别给出了奇异值截断法的计算结果xt的元素值,和本文方法计算结果对比发现,奇异值截断法也能取得较好的精度,但显然操作步骤上比本文方法更为繁琐,也增加了额外的计算量.总体而言,本文方法综合效率最好.

4 结 论

提出了一种统一的奇异值修正公式,以此为基础提出的奇异值修正法,可用于解决测量平差中的病态最小二乘问题.和现有的奇异值截断法或修正法相比,所提新方法更简便快捷,且能获得比奇异值截断法精度更高的计算结果.另外,所提方法普适性强,对方程系数矩阵的维数和是否满秩没有特殊的要求.以两个病态方程为例对所提方法进行了验证,并将计算结果与最小二乘解和奇异值截断解进行了比较,结果说明了所提方法的有效性和优越性.