基于Keras平台的LSTM模型的对流层延迟预测

时瑶佳,吴飞,朱海,韩学法

(上海工程技术大学 电子电气工程学院,上海 201620)

0 引 言

地球大气的最低部分是对流层．它含大约80%的大气质量和99%的气溶胶和水蒸气．17 km是对流层在中纬地区的普遍深度．它在热带地区较深,最高可达20 km,在极地地区较浅[1]．除了各种气体物质存在于对流层中,还有水珠、水汽凝华生成的固态水合物、岩石与金属颗粒等杂质,这些非色散介质会影响电磁波的传输[2]．近年来,随着中国北斗卫星导航系统(BDS)的快速发展,对空间的进一步探索已成为当代科学领域的研究热点．对流层会引起卫星信号的传播延迟,电磁波通过对流层时,会发生传播路径的弯曲和速度的变化,最终测距结果会有误差．因此,天顶对流层延迟(ZTD)成为全球卫星导航系统(GNSS)测量误差的主要来源[3]．所以,充分认识对流层延迟的变化,对于提高导航定位精度是必要的．

当下,常用的对流层折射误差改正方法有参数估算法、差分法、外部改正法、模型改正法[4]．参数估算法会造成待求参量变多,延长了模糊度收敛时间．外部校正法,即GNSS 信号的对流层延迟经由辅助设备如水汽辐射计、激光雷达等校正以获取精度较高的数据，因为设备比较贵重,实际状况下很少使用．但差分计算出的对流层延迟残量也许会使未知数固定失败．模型改正法,即通过分析造成包围地球的空气的折射率改变的大气参数,建立适用在某个区域的对流层延迟模型[5],分成经典模型和经验模型．

模型改正法凭借其廉价和方便的优点,得到了普遍使用,但传统的ZTD模型已很难满足现今高精度定位的需求．机器学习的快速发展使其在时间序列分析领域中发挥着越来越重要的作用,关于对流层延迟预测的机器学习方法也逐渐发展．陈阳等[6]利用反向传播(BP)神经网络误差补偿技术,在Hopfield模型基础上建立了一个适于北半球的融合模型． 吕慧珠等[7]对ZTD的频谱结构进行研究,构造预测模型,该模型的残差被自回归(AR)方法校正,预测达到cm级精度．李伟捷等[8]为提高无气象情况下ZTD预测的精准性,采用一种小波-AR组合模型对IGS中7个测站实现单站ZTD建模预测,均方根误差(RMSE)达到3 cm．任超等[9]提出一种无实测气象参数ZTD预报模型,该模型实现了不同地点和季候下的ZTD估计,精度达cm级．Junping Chen等[10]基于中国地壳运动观测网(CMONOC) GNSS站点和周边地区GNSS站点连续的ZTD时间序列,建立了上海天文台对流层延迟扩展模型,为中国及周边地区的用户提供了精度更高的对流层延迟修正,RMSE达3.5 cm．尹为松等[11]采用安徽省10个连续运行参考站(CORS)的ZTD数据,建立了一种对流层延迟区域内插法,误差达mm级．

上述实测气象参数的经典模型需要大量的输入参数,像气温、压力和水汽压等[12],然而,获取这些气象参数对大多数使用者来说难度较大,这大大限制了他们使用的便捷性．上述无需实测气象参数的经验模型会受天气变化的影响,稳定性较差;存在模型参数不统一,参考性较差;精度较低等缺点[13]．因此,本文提出了一种基于长短期记忆神经网络(LSTM)的ZTD预测模型．该方法利用LSTM能有效捕捉长期的时变信息的优势,只需使用单个测站前期的ZTD时间序列作为输入,预测未来的ZTD数据,这一特点在接收机测试环境下优势更为明显,可行性强,稳定性高,预测精度基本达到mm级,可满足用户的需求．

1 Keras框架简介及LSTM理论方法

1.1 Keras框架

Keras是一个用Python编写的高层神经网络应用程序编程接口(API),它能够以TensorFlow,CNTK或者Theano作为后端运行[14]．迅速把用户的思路转换为实验结果是Keras的研发重心,Keras是做好科研的关键[15]．

Keras的优势是:

1) 对使用者友好:Keras这个API是因人而生的,其考虑的第一要义是使用者的运用感受,它的简便性降低了人们在理解时候的难度,减少了普通应用下使用者的任务量．同时,明确且有实践价值的问题也被提出．

2) 模块化:模型可解释成由独立的、可自由设置的模块构成的序列或运算图．如神经网络层、损失函数、优化器、激活函数模块,可以根据详细需求把它们组合起来构建新模型．

3) 易扩展性:由于现有的模块已经提供了充沛的示例,新模块易仿照其编写新的类,创建新的函数,这种便捷性使Keras在高级钻研中更有优势．

4) 与Python合作:Keras无独立的配置文件, 由Python简洁的代码描绘其模型,调试方便,拓展起来很高效便捷．

1.2 LSTM理论方法

LSTM是循环神经网络(RNN)的一个改进[16]．LSTM由一组称之为记忆块的循环子网构成,每个记忆块包含一个或多个自连接的记忆细胞及三个乘法控制单元——输入、输出和遗忘门,提供着类似读、写、重置的功能[17]．从网络结构设计角度来说,LSTM对标准RNN的改进主要体现在通过门控制器增加了对不同时刻记忆的权重控制,以及加入跨层连接削弱了梯度消失问题的影响[18]．

LSTM记忆块结构示意图如图1所示．符号⨁代表两个向量的加法运算,符号⊗代表两个向量的点乘运算,σ为sigmoid激活函数,tanh为双曲正切激活函数．

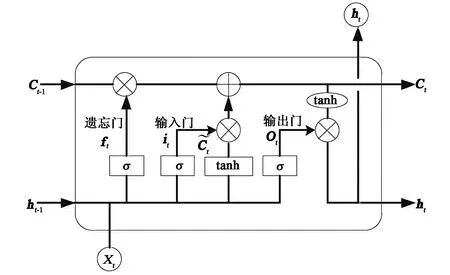
图1 LSTM记忆块结构示意图

LSTM通过门控制器增加了对不同时刻记忆的权重控制,记忆块数据更新的过程如下:

1) 经由遗忘门的sigmoid单元来决定细胞状况需要抛弃的信息．

ft=σ(Wf·[ht-1,xt]+bf).

(1)

式中:ft为遗忘门输出;Wf,bf分别为遗忘门的权重矩阵和偏移向量;σ为sigmoid激活函数,σ∈(0,1);ht-1为上一个细胞的输出;xt为当前细胞的输入．

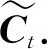
it=σ(Wi·[ht-1,xt]+bi).

(2)

(3)

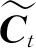
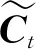
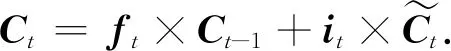
(4)

式中，Ct-1、Ct分别为上一时刻和当前时刻的细胞信息．

4) 状态输出,分为两个步骤．起初,输出门的sigmoid层经由ht-1和xt,细胞状态的输出部分被选定．下一步是,tanh层通过了更新的细胞状态Ct,得到一个向量,值为-1～1．最后一步是sigmoid层的输出与该向量相乘获取整个单元的输出ht．

ot=σ(Wo[ht-1,xt]+bo).

(5)

ht=ot×tanh(Ct).

(6)

式中:ot为输出门输出;Wo、bo分别为输出门的权重矩阵和偏移向量．

2 ZTD预测模型的构建

LSTM的网络结构即预测过程如图2所示,整个LSTM网络由若干个记忆块组成,上一时刻的细胞信息和整个记忆块的输出会传入下一个记忆块中以进行数据更新,其中LSTMt为t时刻的记忆块．LSTM的网络结构由L确定,L为神经网络的窗口长度,该参数表示利用时间长度为L的历史数据输入网络以预测下一时刻的数据．

图2 LSTM网络结构示意图

2.1 站点数据源

本文使用的对流层延迟数据来源于国际GNSS服务(IGS)提供的高精度ZTD产品,数据间隔为5 min[19],选取了全球均匀分布的8个测站作为实验测站,分别是scor,mars,aruc,ykro,riop,alic,falk,syog测站,提取其1 h间隔的ZTD数据,数据的时间范围是2016年第90—136年积日．各站点的经纬度及海拔如表1所示,测站分布如图3所见,其中红色点代表8个实验站点的所在位置．

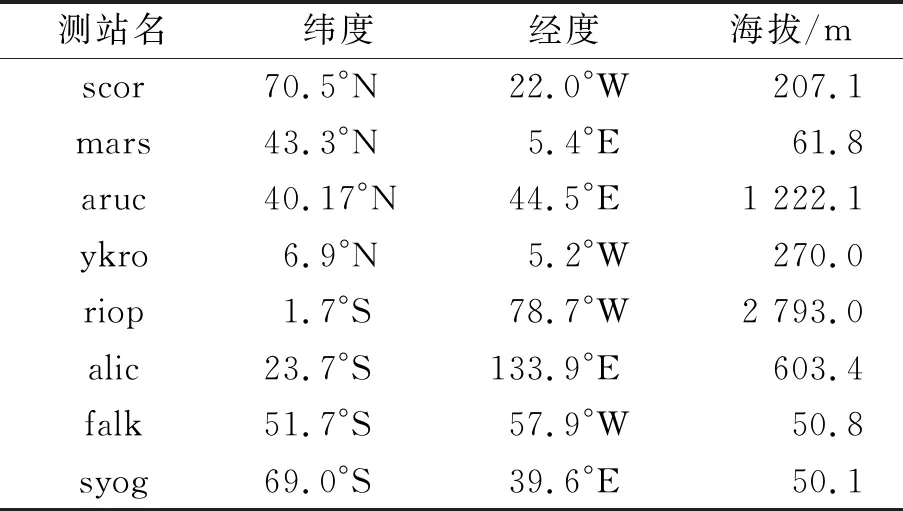
表1 8个实验测站的经纬度及海拔

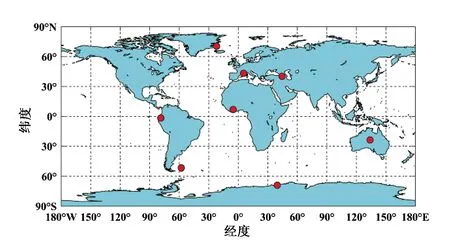
图3 测站分布图

2.2 LSTM模型的构建

用Keras建立模型一般包括数据预处理、定义模型、训练模型、评估模型准确率和进行预测这几个阶段．

设对流层延迟时间序列为x={xt},t=1,2,3,…,n,其中,xt为t时刻的对流层延迟．给定神经网络的窗口长度L,该参数表示使用时间长度为L的历史对流层延迟xt,xt+1,…，xt+L-1序列来预测下一时刻的对流层延迟pt+L[20]．对ZTD进行训练和预测过程具体如下:

步骤1:网络初始化．

设定窗口长度L为3,特征数量amount-of-features为1,dropout系数为0.05,批训练数量batch-size为16,总迭代次数epoch设为100．

步骤2:数据归一化．

由于数据是每一小时的对流层延迟,即只有一个属性值,因此不需要归一化操作．

步骤3:划分数据集．

划分x为训练集xtrain={x1,x2,…，xd}和测试集xtest={xd+1,xd+2,…,xn}．根据L对训练集划分子集,结果为{{xtrain1},{xtrain2},…{xtraint},…,{xtraind-L+1}},其中xtraint={xt,xt+1,…,xt+L-1}．

步骤4:构建LSTM网络．

本文运用了Keras中最主要的Sequential层次模型,即一层层线性叠加的网络架构,构建方式为:model=Sequential()．激活函数使用relu函数．使用的损失函数为均方误差(MSE),优化器为自适应矩估计(Adam)．

步骤5:将网络训练好后,进行迭代预测．

首先,使用训练子集中的最后一个子集{xtraind-L+1}得到第一个预测值pd+1,将此值与{xtraind-L+1}的后L-1个值合并成新子集{xd-L+2,xd-L+3,…,xd,pd+1},将该子集输入到网络中得到下一个预测值pd+2,以此类推,即可得到所有的预测值{pd+1,pd+2,…,pn}．

3 实验结果与精度分析

为了验证LSTM模型在对流层延迟预测方面的性能及广泛性,鉴于实验数据完整性准则,本文选取全球均匀分布的,实验数据完整的8个测站．利用IGS提供的其2016年第90～136年积日,共47 d的整点数据为样本数据,样本数据中前42 d共1 008 h的数据作为训练数据,后5 d共120 h的数据作为测试数据．本文采用Python 3.8语言与Keras2.4函数库实现建模,建立了8个测站的LSTM对流层延迟预测模型．将LSTM模型与BP神经网络的预测结果对比分析,验证LSTM模型的可靠性．

作为对比的BP网络也采用Keras平台,其与LSTM最大的区别在于BP是一个全连接网络,各层神经元仅与相邻层神经元之间相互连接,同层的神经元之间不连接,具体网络连接顺序为输入层、4层隐藏层、输出层．BP网络使用relu为激活函数,采用Adam优化函数实现梯度下降,其余参数与LSTM基本一致,包括dropout设为0.05, batch-size设为16, epoch设为100等．

本文算法的开发环境是Win10操作系统下的TensorFlow4 2.3框架,运行的硬件环境为英特尔酷睿i7-8750H@2.2 GHz处理器,内存是16 GB．

3.1 单个测站预测结果与分析

本文选取了全球均匀分布的8个测站作为实验测站,其中ykro,riop,alic处于低纬地区,mars,aruc,falk处于中纬地区,scor,syog处于高纬地区,LSTM模型,BP神经网络模型的预测结果如图4所示．

(a)scor站 (b)mars站

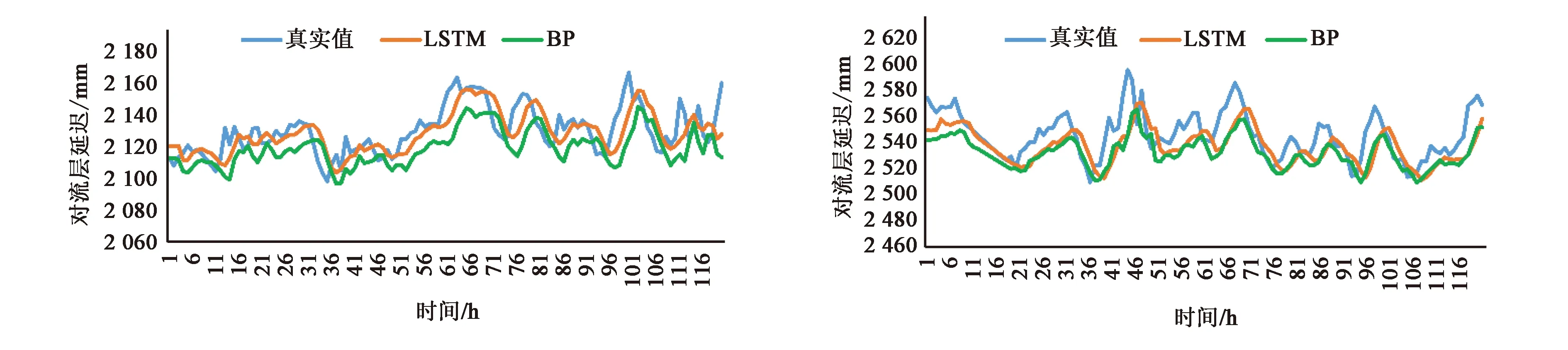
(c)aruc站 (d)ykro站

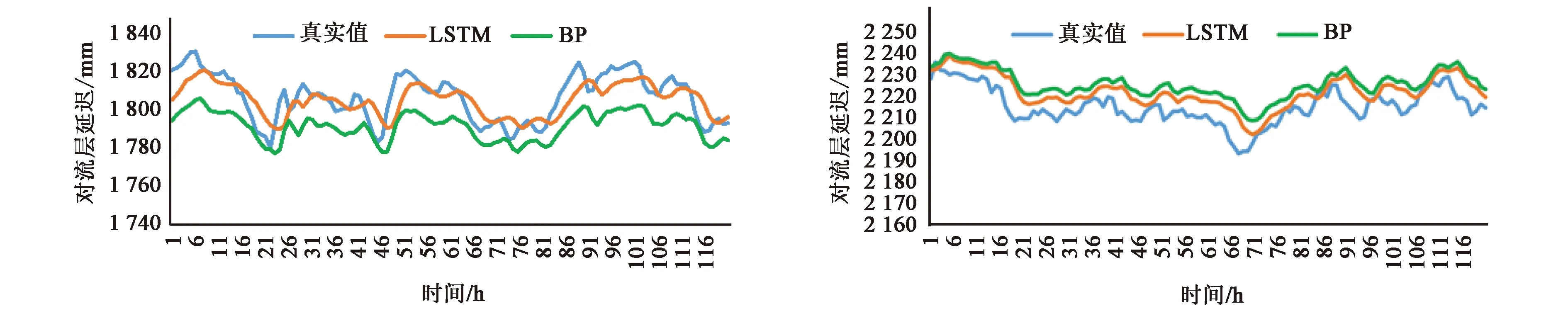
(e) riop站 (f)alic站

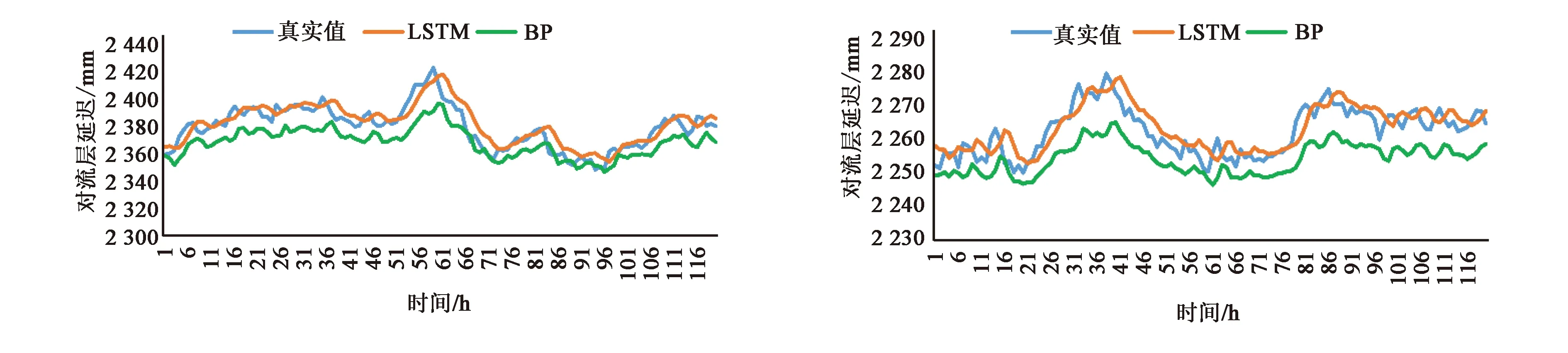
(g)falk站 (h)syog站图4 各站点在两种模型下的预测结果

从图中可以看出,LSTM模型对对流层延迟的预测比较准确,BP模型预测的结果与真实值的差距较大,且存在预测效果不稳定的情况．总的来说,LSTM模型预测效果在全球均匀分布的8个站点中均优于BP模型．其中,北纬地区的scor,mars,aruc测站的预测效果优于ykro测站, 南纬地区的falk,syog测站的预测效果优于riop,alic测站,说明中高纬地区的LSTM模型预测效果优于低纬地区．

3.2 精度分析

为了验证LSTM模型对ZTD预测的准确性,选择了8个实验测站中的alic测站,利用散点图直观地表现出真实值与模型预测值之间的总体关系趋势,散点图如图5所示．alic站的LSTM模型预测效果在所有实验测站中处于较低水平,因此可以大致代表所有实验测站的散点图情况．

(a)alic站 (b)alic站图5 alic站两种模型ZTD预测结果散点图

根据图5,对比两种模型的预测结果散点分布情况可以看出,LSTM模型的预测值与实际观测值更加贴切,说明其预测精度更高,决定系数R2达到了0.725 8,而BP模型的决定系数R2为0.704 9,比LSTM模型低了约0.02．由此说明,LSTM模型的预测效果优于BP模型．

相比于BP模型,LSTM要训练的参数增加,如Wf,Wi,Wo,Wc等,因此数据关联性和准确度也会增加．另外BP模型在实验过程中存在一个较为严重的问题,由于BP模型的本质是梯度下降法,根据设置的目标函数去求取最优解,这样就必然会出现局部鞍点和不收敛的情况,而LSTM则是基于RNN的改良,并且解决了RNN中梯度爆炸和梯度消失的问题,从理论层面是优于原始BP模型的．

为进一步验证LSTM模型的精度,本文使用RMSE、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)为精度指标,计算结果如表2所示,计算公式为:

(7)

(8)

(9)

式中：ot,pt分别为t时刻对流层延迟的观测值和预测值;n为测试集中数据的个数．

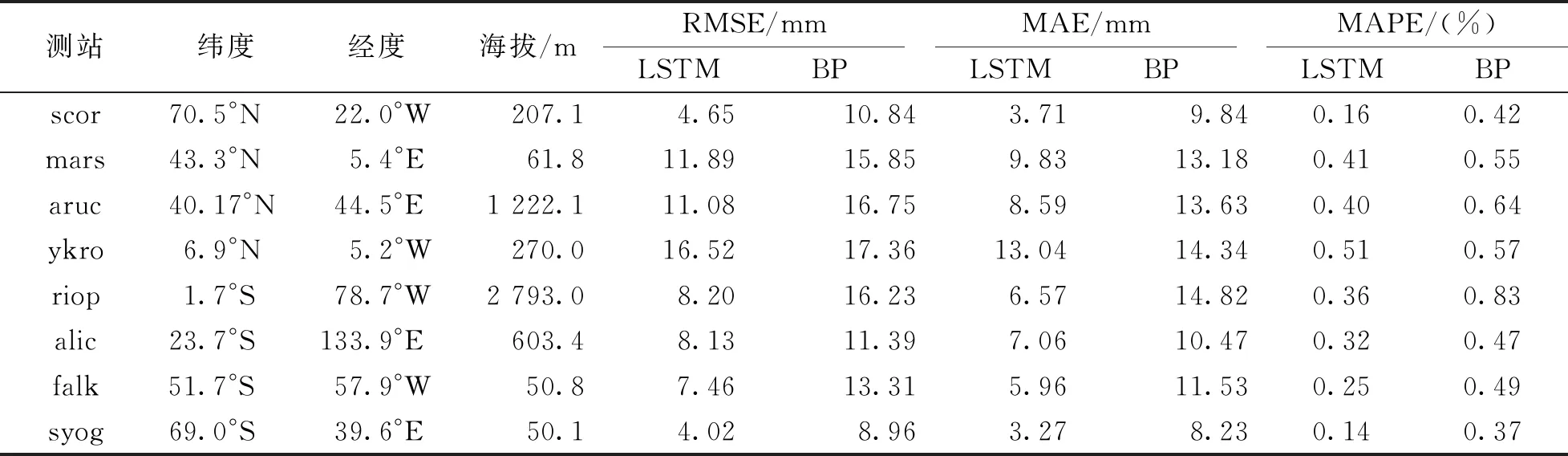
表2 2个模型预测结果的RMSE,MAE及MAPE对比站

根据表2,本次实验LSTM模型在8个测站中的RMSE,MAE,MAPE均比BP模型低,LSTM模型中,有5个站点的RMSE达到mm级,BP模型中,有1个站点的RMSE达到mm级;LSTM模型中,有7个站点的MAE达到mm级,BP模型中,有2个站点的MAE达到mm级;LSTM模型的MAPE均小于0.51%,BP模型的MAPE均小于0.83%,LSTM模型在全球的预测精度明显高于BP模型．

LSTM模型的预测精度基本达到mm级,适用于对流层延迟的预测,且更适用在中高纬地区．

4 结束语

本文通过提取IGS中心提供的全球均匀分布的8个测站2016年第90—131年积日ZTD真值训练LSTM模型,构建了一种无需实测气象参数的预测新方法,预测了该8个测站第132—136年积日的ZTD．结果表明:1)基于LSTM神经网络的对流层延迟预测模型,其建模方法简单,易于使用;2) LSTM模型预测结果的RMSE达到mm级的约占62.5%,BP模型预测结果的RMSE达到mm级的约占12.5%,LSTM模型的MAE和MAPE均比BP低．LSTM模型在精度和稳定性上较BP模型均有显著提高;3)LSTM模型更适用于中高纬地区的对流层延迟预测．

论文证明了将LSTM神经网络应用到定位与导航领域中对流层延迟时间序列预测的可行性．由于本文选取的8个测站(scor,mars,aruc,ykro,riop,alic,falk,syog)经纬度,海拔存在较大差异,因此文章所得结论排除了一定的偶然性．