FDFA及其在发动机故障诊断中的应用

武书彦，邹建华，吴青娥,许明喆，胡博

(1.西安交通大学 电子与信息工程学院, 陕西 西安 710049;2.河南牧业经济学院 信息工程学院, 河南 郑州 450046;3.郑州轻工业大学 电气信息工程学院, 河南 郑州 450002)

0 引言

单位模糊自动机在模糊自动机半群中的某一时刻会对应多种不同的状态，每一种状态都对应着不同的可信度，这样模糊自动机半群就能与现实世界和客观事物比较贴合，能够比较真实地反映现实世界。但是半群自动机的推导等价并不容易实行，即便是对复杂程度较低的有限半群自动机也有一定的困难。

在神经网络技术和模糊技术发展的背景下，模糊自动机得以快速发展并取得了广泛的应用[1-3]。在现代战争方面的应用尤为突出，面对狡猾的敌人如何识别真相是一个难题；又如列车前方障碍物的识别、汽车防撞雷达、无人机的目标探测、潜艇的障碍物闪避等，运用模糊神经网络自动机(Fuzzy neural network automaton, FNNA)[4-6]能够轻松达到灵活、快速、准确地做出判断处理的效果。而且在通信领域FNNA中模糊自动机发挥的作用将越来越大。模糊推理在社会的诸多领域起到了重要的作用，尤其是控制系统以及人工智能领域。具有不确定性数据之间的相似性特点通常可以模糊集与闭区间将它们的特征表示出来，根据这种特性，有些学者提出了区间分析方法[7-12]。为了提高自动机的诊断效果，可以将其与模糊集的方法相结合，提出模糊自动机半群的模糊推理，并将其应用于机器故障诊断中。YAGER[13]在多值模糊关系研究基础上，进一步探究了两种形式的模糊推理，分别是简单多值模糊推理和多重区间值的模糊推理。模糊推理进行时，影响因素的大小可能会产生不同的结果，因此可以对影响大的因素分配较大的权重，影响小的因素分配较小权重，这是一种符合人的正常思维过程的想法。

在前期的工作中，已讨论过一种类型的FDFA代数系统，即格。格〈M,∨|∪,∧|∩〉具有两个二元运算。在本文中，将讨论具有一个二元运算的代数系统，即半群。这些理论在自然科学以及应用科学领域都起到了不小的作用。例如，在信息安全与编码理论中就用到半群。

1 半群

设F=[0，1]，G是Q中的模糊集，Gλ为集合G的截集Gλ={x∈Q|G(x)≥λ,λ∈F}，显然Gλ⊆Q。定义λG={G(x)|G(x)≥λ,λ∈F,x∈Q}，显然λG⊆F。

定义1对FDFAM输入Σ*中的一个字符序列ω后，以某一隶属度μ，由Q的每一个状态p都要分别变到另外一个状态q，因此，(ω,μ)引导出状态集合Q到Gu上的一个变换δ(qi,ω,μ)={qj},∀μ∈F，即Q上的一个变换。所有由(ω,μ)引导出的变换“·”，即{qj}·{ql}={qn}。若FDFAM(M,·)满足结合律，即对于任何m1= (Q1,Σ1,δ1,q01,G1,F1)，δ1(qi1,a1,μ1)={qj1}；m2= (Q2,Σ2,δ2,q02,G2,F2)，δ2(qi2,a2,μ2)={qj2}；m3= (Q3,Σ3,δ3,q03,G3,F3)，δ3(qi3,a3,μ3)={qj3}；m1,m2,m3∈M，有m1·(m2·m3)=(m1·m2)·m3，即{qj1}·({qj2}·{qj3})=({qj1}·{qj2})·{qj3}，则称FDFAM(M,·)为半群，有时就称M为半群自动机。

例1由FDFA引导出的一个确定的有限态自动机(DFA)D=(Q,Σ,δa,q0,Gλ)，这里定义δa(q,ω)=p⟺δ(q,ω,a)=p,q,p∈Q,ω∈Σ*，a∈F。则FDFA到DFA的变换构成半群，且(D,∩)和(D,∪)也都是半群。

定义2将FDFA与M进行二元运算·，它们作为具有单位元的半群，相当于对所有m1= (Q1,Σ1,δ1,q01,G1,F1)，m2= (Q2,Σ2,δ2,q02,G2,F2)，m3= (Q3,Σ3,δ3,q03,G3,F3)，m1,m2,m3∈M，有m1·(m2·m3)=(m1·m2)·m3，并且有元素e∈M，对于任何m1∈M，有m1·e=e·m1=m1，则称(M,·)为含单元半群。

FDFAM中存在e= (Q,Σ,δ,q0,G,F)，定义δ(q,ω,μ)=q，这里ω∈Σ*,q∈Q，μ∈F和G0=Q。

显然，含单元半群的单位元是唯一的。

在半群(M,·)中，规定mn=m·m·…·m。因此，对于任何正整数l,n，∀m∈M，有ml·mn=ml+n，(ml)n=mln。

若(M,·)是含单元半群，规定m0=e(单位元)。

假如(M,·)的二元运算“·”在半群自动机以及含单元半群自动机过程中是可进行交换的，即∀m1,m2∈M，m1·m2=m2·m1，则称(M,·)是可换半群或含单元半群自动机。

在半群自动机(M,·)中，如果元素m满足m·m=m，则称m是幂等的。若m为幂等元，则mn=m，每个含单元半群至少包含一个幂等元素，即单位元。

定义3设(M,·)是一个半群自动机，这里M={(Qn,Σn,δn,q0n,Gn,Fn)|n∈N}，对应δn(qi,a,μ)={qj}；Mi={(Qi,Σi,δi,q0i,Gi,Fi)|i∈N}，对应δi(qk,ω,λ)={ql}，这里，qj∈Gn，ql∈Gi。假设Mi作为M的有元子集，可得Qi⊆Qn，Σi⊆Σn，δi(ql,ω,λ)⊆δn(qi,a,μ)，q0i=q0n，Gi⊆Gn，Fi⊆Fn，Mi进行二元运算“·”是密闭进行的，即对于∀m1,m2∈Mi，有m1·m2∈Mi，即{qj}·{ql}={qn}⊆Gi，则称(Mi,·)是(M,·)的子合单元半群自动机。

定义4设(M,·)是一个含单元半群自动机，M1是M的子集，如果M1对运算·是封闭的，且M的单位元e∈M1，则称(M1,·)是(M,·)的子群自动机。

从定义可以看出，子半群自动机本身是一个半群(含单元半群)自动机。

定理1对于任何可换的含单元半群FDFA (M,·)，M的幂等元的集构成一个子含单元半群自动机。

证设T是M中的幂等元的集，因为单位元e是幂等元，所以e∈T。对于∀t1,t2∈T，于是t1·t1=t1，t2·t2=t2，由于(M,·)可交换，故

(t1·t2)·(t1·t2)=(t1·t2)·(t2·t1)=t1·(t2·t2)·t1=t1·t2·t1=t1·t1·t2=t1·t2，因此，t1·t2∈T，即(T,·)是(M,·)的子含单元半群。

定义5设(M,·)和(T,*)是两个半群自动机，映射f:M→T称为M到T的半群自动机同态映射，假如对于∀m1,m2∈M，有

f(m1·m2)=f(m1)*f(m2)，

假如f作为自动机的满映射，就将f称作自动机的满同态；假如f作为自动机的单映射，就将f称作自动机的单一同态；假如f作为自动机的双映射，就可以将f作为M到T的同构映射。如果半群自动机M和T之间存在同构映射，则称M和T同构，记为M≅T。

定理2设f是FDFA(M,·)到(T,*)半群同态映射，则对于任何幂等元m∈M，f(m)也是幂等元。

证因为m是幂等元，即m·m=m，于是

f(m·)m=f(m)=f(m)*f(m)，

即f(m)是幂等元。

定义6设(M,·)和(T,*)是两个含单元半群自动机，映射f:M→T称为M到T的含单元半群自动机同态映射，假如对于∀m1,m2∈M，有f(m1·m2)=f(m1)*f(m2)，f(eM)=eT，这里eM，eT分别是M与T的单位元。

定理3设FDFA半群自动机(M,·)，(T,*)，这里“·”，“*”分别是M和T的二元运算，且f是M到T的满同态映射。

① 如果(M,·)是半群自动机，则(T,*)也是半群自动机。

② 如果(M,·)是含单元半群自动机，则(T,*)也是含单元半群自动机，且单位元对应单位元。

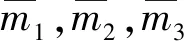
而:

由假设

m1·(m2·m3)=(m1·m2)·m3,

于是(T,*)是半群自动机。

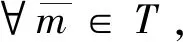
因此，eT是T的单位元，即(T,*)是含单元半群自动机。

定理4设FDFA(M1,*1)，(M2,*2)和(M3,*3)都是半群自动机，且f:M1→M2，g:M2→M3都是半群同态映射，则(g·f)是M1→M3的半群同态映射。

证设对于任何m1,m2∈M1，有

(g·f)(m1*1m2)=g[f(m1*1m2)]=g[f(m1)*2f(m2)]=

g(f(m1))*3g(f(m2))=(g·f)(m1)*3(g·f)(m2)。

因此，(g·f)是M1到M3的半群同态映射。

2 FDFA半群的推理及应用

2.1 FDFA半群的推理

根据模糊自动机推理的特点，可总结定义如下：

定义7模糊自动机推理是运用模糊语言和自动机的一种映射转变关系，对模糊现象进行模糊判断，推导出一个与模糊结论相近的解决方法，是一种不确定性推理方法。

FDFA半群的多输入模糊推理由以下两种推理构成。

2.1.1FDFA半群的多态模糊推理

多态模糊推理经常出现在多—单系统的设计里面，例如，在运动机械动力部分的速度值控制调整系统中，“如果速度误差以及速度误差的变化量也同样较大，就需要增加控制电压”这类规则控制就可以采用FDFA半群的多态模糊推理机制来解决。

对于矩阵A，B，C，这种规则的一般形式可表示如下：

前提1：如果A且B，那么C，

前提2：现在是A′且B′。

结论：C=(A′ andB′)·[(AandB)→C]。

如果各语言变量的论域通常都为非无限集，因此隶属度函数作为有限集的模糊子集是离散的，在这种情况下采用模糊控制的关系矩阵运算方法是简易的。已知如果存在当A且B的关系时，则有输出为C，即矩阵A、B、C存在以下的推理规则:

ifAandB, thenC，

求当A′和B′，控制输出C′应该多少可以用以下步骤：

① 先求矩阵D=A×B，令dxy=μA(x)∧μB(y)得D矩阵:

② 将D写成列矢量DT，即DT=[d11,d12,…,d1n,d21,…dmn]T。

③ 求出关系矩阵R，R=DT×C。

④ 由A′、B′求出D′，D′=A′×B′。

⑤ 仿照②。将D′转化为行矢量DT′。

⑥ 最后求出输出的模糊推理。

2.1.2FDFA半群的多输入多规则模糊推理

如果A1且B1，那么C1。

否则如果A2且B2，那么C2。

……

否则如果An且Bn，那么Cn。

已知A′且B′，那么C′=?

C′=(A′ andB′)·([(A1andB1)→C1])∪…∪([(AnandBn)→Cn])=C1′∪C2′∪C3′∪…∪Cn′。

其中，Ci′=(A′ andB′)·([(AiandBi)→Ci])=A′→(Ai→Ci)∩[B′·(Bi→Ci)],i=1,2,3,…,n。

对于上述的多态多规则总的推理结果是将每一个推理规则的模糊关系矩阵进行“并”运算就可以了，相当于对以上所有的推理规则，都能计算出相符合的模糊关系矩阵。

Ri=Ai×Bi×…×Ci,i=1,2,3,…,n。

在上式中直积算子“×”可采用“极小”运算，对上述式子进行 “代数积”运算。

系统总的控制规则所对应的关系矩阵R通常采用并的算法求出，即

R=R1∪R2∪…∪Rn。

2.2 FDFA半群的多维模糊推理在运动装置旋转机械故障诊断中的应用

本文通过分析未处理的故障数据，基于FDFA半群模糊推理的模糊技术对模糊几何特性属性进行处理，从而达到故障诊断的效果。下面通过一个发动机故障诊断的例子，展示一下FDFA半群的多维模糊推理在发动机故障诊断中的应用。

2.2.1 征兆/故障样本集的收集与设计

发动机在高负荷和长时间运行时，容易导致油路和气路发生故障。但是发动机的内部结构比较复杂，不易准确和快速找到其故障点。所以下面尝试利用FDFA半群的模糊推理来实现对发动机的故障诊断。

发动机运行时常有6种参数表示其运行状态，它们分别是MA、AA、MD、AD、TR和RS。其中,MA表示发动机运行的最大加速度，AA表示发动机运行的平均加速度，MD表示发动机运行的最大减速度，AD表示发动机运行的平均减速度，TR为表示发动机的扭矩谐波分量比,RS表示发动机的燃爆时的上升速度。

在进行诊断时，需通过FDFA半群模糊推理技术对提取的相关特征参数进行分析，具体过程如图1所示。

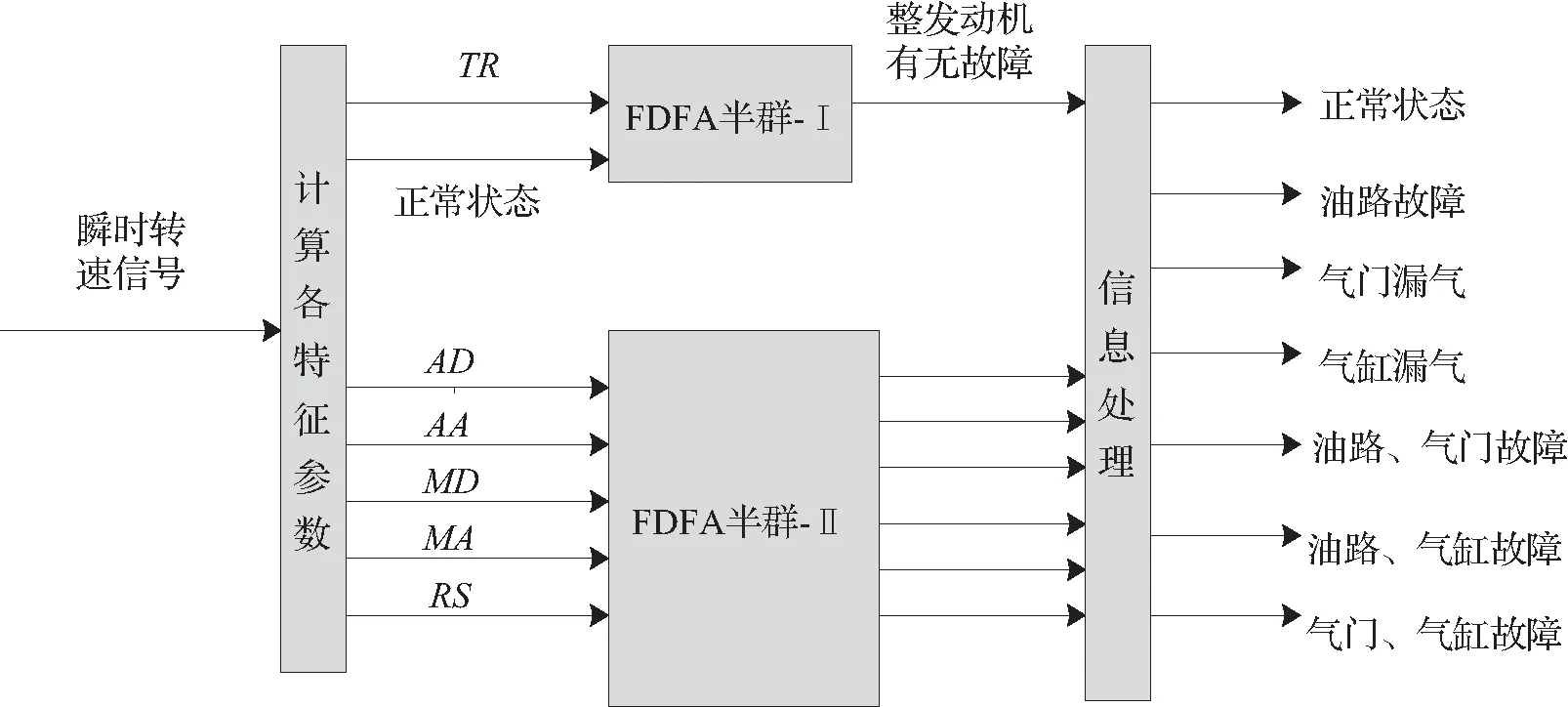
图1 基于FDFA半群的模糊推理的发动机诊断模型Fig.1 Engine diagnosis model based on fuzzy reasoning of FDFA semigroup

这里主要介绍如何利用FDFA半群的模糊推理进行故障诊断，通过对于发动机1号气缸的分析可知，自动机的1号气缸一共发现了3种故障，它们分别是油量不足、气门漏气和气缸漏气，如果算上正常模式，可以把故障归结为4种。本文采用二进制格式对不同的故障类型进行描述，见表1。这4种故障通过大量的现场实地考察和历史资料的汇总分析，总结出了四组故障的样本数据，见表2。

表1 故障模式分类Tab.1 Classification of fault modes

表2 故障样本数据Tab.2 Fault sample data

使用上面列表中的数据训练FDFA半群，经2 000次迭代过程，以均方误差最小为其训练的性能指标。其模糊推理过程如图2所示。

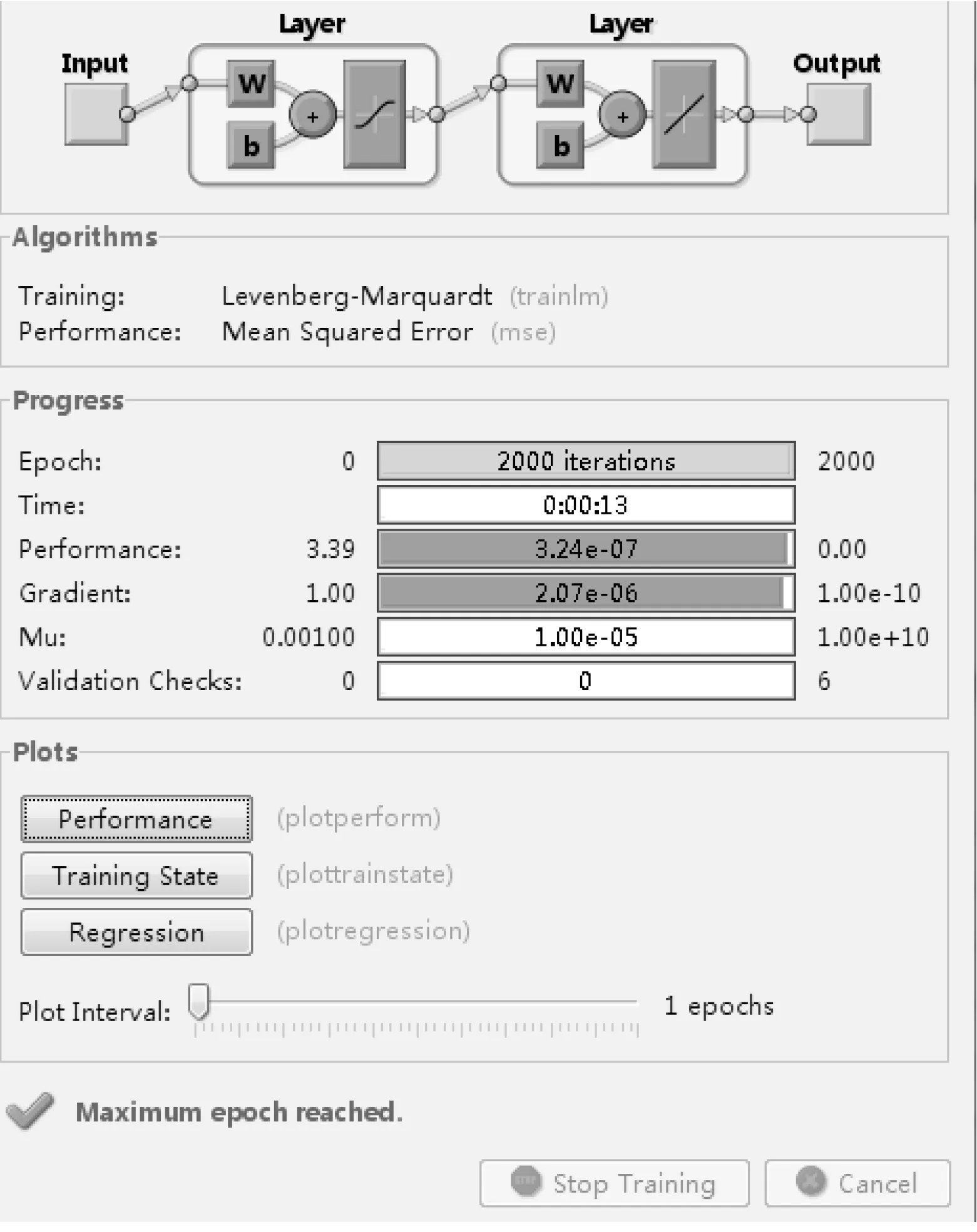
图2 FDFA半群的模糊推理的训练过程Fig.2 Training process of fuzzy reasoning for FDFA semigroups

程序运行，由仿真得分类结果为：faultclass =[1, 2, 3, 4]。由仿真结果可知，FDFA半群的模糊推理成功地对上述故障模式进行了分类，这与表2中的数据是吻合的，共四种故障模式类。

为了测试FDFA半群自动机进行模糊推理时的外推性能,给出一组测试样本数据,见表3。这些数据采集的是机械真实的故障数据,可以准确地测试出FDFA半群的模糊推理的故障检测性能。

表3 故障样本数据Tab.3 Fault sample data

采用训练样本以外的数据对网络进行测试，是一种最好的测试方案。现对表3所示的测试样本数据进行测试，仿真结果也为faultclass =[1, 2, 3, 4]。由仿真结果可知，FDFA半群的模糊推理也能成功地对上述测试样本数据进行了分类，这与表3的4种故障模式数据也是吻合的。

由FDFA半群的模糊推理的MATLAB仿真结果可知，FDFA半群的模糊推理的诊断结果是正确的。也就是说，FDFA半群的模糊推理成功地诊断出了这4种故障，因此，FDFA半群的模糊推理用于故障诊断是有效的。

2.2.2 FDFA半群的输出向量设计

为了方便找出故障所在，本文将发动机故障的严重程度划分为3个等级Fi，这里i为发动机故障的级别，即1级严重故障、2级中等故障和无故障(正常)。根据FDFA半群的模糊推理的输出向量，得到以下结果。

若0.75

若0.25

若Fi<0.25或者Fi>1.50，则Fi=正常(无故障)。

所以可以通过得出的结果来判断发动机故障的严重程度。

用一组实际数据对FDFA半群的模糊推理进行检验，从本次测试中可以看出FDFA半群的模糊推理是否能够正确诊断出发动机增压系统中的故障。如果可以正确诊断出故障，则FDFA半群的模糊推理可以投入使用。分别在F2、F3和F4出现故障时进行检测，获取到各参数的值，将得到的这些值作为输入向量，对FDFA半群的模糊推理输出采用仿真函数进行推理计算，并且对故障点进行故障判别准则判断出故障原因。测试数据见表4。

表4 测试数据Tab.4 Test data

编写代码进行仿真，运行程序，输出如下：

output 1=[2 3 4 5];

output 2=[2 3 4 5];

output 3=[2 3 4 5]。

由分析结果可知，FDFA半群的模糊推理成功地诊断出了所有故障，这与表4中的数据是吻合的，因此，可以将该FDFA半群的模糊推理投入实际工程应用。

本文对故障数据采用基于FDFA半群的模糊推理等技术，得出结论：在应用该技术处理发动机故障问题后，不仅系统推理速度明显提高，而且还使推理系统的识别精度更加理想化。对如表3中的大量样本数据，FDFA半群的模糊推理对故障数据的跟踪如图3(a)所示。对如表4中的大量测试数据，FDFA半群的模糊推理对故障数据的跟踪如图3(b)所示。

(a) 对表3故障数据的跟踪

如果所研究的问题很复杂，有很多不确定的因素，那么，FDFA半群逻辑为解决此问题提供了一个合适的工具，使我们可以很快为一个系统建模，并在多种模型和方法中选择合适的一个。

3 结论

本文给出了模糊自动机半群的定义及其性质，给出了FDFA半群的推理方法，并讨论了FDFA半群的推理方法在发动机故障诊断中的应用。针对FDFA半群的多维模糊推理，提出了一种阈值、规则的模糊推理方法，构造了FDFA半群的推理系统。本文设计的系统在对数据进行预处理前，首先会给每个规则条件赋予一个适当的阈值向量,对一些影响小的因素进行筛检，从而清除一些无用的规则,并提高了最终输出结果的精度，所以在此方案基础上得出的推理方法与实际推理更加接近，便于日常工程应用。

一个值得思考的问题是，是否能把几个不同的半群自动机组合，去处理多个模糊知识的叠加，以及由神经网络怎样抽取这个组合的半群自动机?我们接下来将会对这个问题进行探索。