机械密封动环结构动力学特性研究与试验分析

邹昕桓 陈 庆 高 路

(吉林化工学院 吉林吉林 132022)

机械密封是一种依靠弹性元件对动、静环端面密封副的预紧及介质压力的双重作用而达到轴向密封的装置，又称为端面密封。按端面比压(pc)大小可以分为接触式机械密封(pc>0)和非接触式机械密封(pc=0)。机械密封早期的端面材料单一，磨损量和使用寿命较短。随着材料科学的不断发展和新技术的诞生，新型陶瓷、合金及镀膜材料在机械密封上的应用，使得其具有磨损小、寿命长、耗能低、泄漏量少、工作状态稳定及适应性强等优点，被广泛应用在航空航天、石油化工、船舶、汽车等领域[1]。

机械密封端面在加工和研磨时存在误差，使得其端面在加工波度和表面粗糙度的影响下有着大小不一的微凸体，尤其是在接触式机械密封中，这些微凸体导致表面液膜并不完整，形成混合摩擦。在实际工况下，机械密封不仅受到温度、压力等因素的影响，设备的振动同样会影响机械密封的使用效果。振动会增大密封面的相对滑动，导致液膜厚度不均匀，增大密封副之间的干摩擦面积。大小不一的微凸体会使动环和静环之间的犁削作用加剧，摩擦端面产生的磨损会高于润滑条件良好状态下几个数量级，进而导致泄漏[2]，加速机械密封的失效。

在机械密封研究方面，文献[3]提出了一种磨损率的计算方式；文献[4-7]建立了机械密封端面接触模型，并根据W-M函数确定表面微凸体的主要变形为弹性、塑性及弹塑性；文献[8]构造了BP神经网络模型,对机械密封端面间的膜厚进行检测。根据Archard磨损理论[9]可知，摩擦副中软质环在载荷的作用下会发生形变，在摩擦力及轴向振动的影响下其微凸体会被剪断，形成杂质。过多的杂质会加快端面间的磨损进而导致失效。在机械密封动力学研究方面，文献[10-12]证明了转子系统的振动会受到机械密封的抑制，并推导和建立了机械密封静环的动力学方程；文献[13]建立了静环动力学模型；文献[14]提出动环的轴向位移会影响静环稳定性。但上述研究对机械密封端面磨损及低速气体端面密封的动力学分析较少[15]。在实际工况中机械密封的失效是不可避免的，其主要的失效形式表现为端面的磨损，所以对机械密封的动态分析是十分必要的。

本文作者以某浓缩循环泵用机械密封为例，依据模态分析理论[16]，采用有限元分析软件对机械密封的动环进行有限元结构分析，得到动环的各阶模态和应变云图，并通过试验加以验证。

1 有限元分析

1.1 模态分析理论

模态分析将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦[17]，得到结构模态空间的固有频率、振型、模态质量、模态刚度等。其矩阵形式的非线性结构方程[18]为

(1)

(2)

(3)

将公式(2)、(3)代入公式(1)得到公式(4)：

(4)

由公式(4)可知：结构的质量、阻尼、应力、刚度、材料密度和外载荷均对结构的模态产生影响。在模态分析中假设结构为线性，即：结构质量矩阵[M]和结构刚度矩阵[K]为常值，F[t]=0。一般阻尼[C]=0.001～0.1，对结构的固有振型影响很小，固将非线性结构方程简化为线性无阻尼结构方程[19],即

(5)

假设结构的运动简谐方程为

{u}={φ}isin(ωi+θi)

(6)

(7)

将结构位移、速度方程代入控制方程中可以得到特征方程：

([K]-ω2[M]){φi}={0}

(8)

式中:ω为固有频率；{φ}为结构振型；θi为初相位。

当{φi}=0时，表明该结构没有振动，故舍去。所以该方程的解可以化简为

det([K]-ω2[M])={0}

(9)

1.2 有限元建模

用SolidWorks对泵用机械密封动环进行三维建模并化简，动环参数见表1。在ANSYS中对三维模型离散化，并打开高级尺寸控制，对圆边进行优化，得到了56 993个节点和36 911个单元。动环模型如图1所示。

表1 机械密封动环静环参数

图1 机械密封动环模型

Fig 1 Movable ring model of mechanical seal

1.3 有限元分析

由于机械密封动环的轴向运动受到静环和弹簧力的约束，因此在有限元分析中假设动环轴向运动被固定，抑制其轴向自由度。在动环内壁处加Cylindrical Support限制了径向自由度，周向自由度没被限制。动环受到弹簧的作用力，外部受到介质压力，内径受到轴的支撑力。机械密封在运行过程中，摩擦副端面由于结构振动引起的相对滑动会加大零件扭转变形，使动环和静环之间的切削作用增大，导致机械密封动环的端面磨损量和变形量增大。用有限元分析软件ANSYS Workbench对动环进行力学分析。工程中为减少工作量，一般取前10阶或前20阶模态进行分析。文中模拟取前10阶模态进行分析。其模态如图2所示。

图2 机械密封动环前10阶振型Fig 2 The first ten vibration modes of the mechanical seal movable ring

结果表明，机械密封的动环主要振型有：径向产生相对扭转，如1阶、2阶、3阶模态；两边向圆心方向发生弯曲，如4阶、5阶模态；密封面沿径向摆动，如6阶、7阶模态；端面产生相对拉伸，如8阶模态；端面处整体产生很大的形变，如9阶、10阶模态。在动环模态分析中，其应变随着固有频率的增加而增大，第1阶与后9阶的固有频率有极大的差距，从第4阶到第9阶，频率变化稳定，每一阶模态应变大小不同。各阶振动的频率与应变关系见表2。

表2 频率与应变之间对比

由表2可知，与1阶模态比较，2～10阶模态振动频率高，动环的形变量大。振动使端面产生扭转变形，相对滑动增大，接触面积变大，微凸体之间的间隙减小，微米级别的液膜厚度会随着端面形变和微凸体之间的间隙减小而逐渐减小，使液膜分布不均匀，密封面形成干摩擦，加快了密封面的磨损，减少了有效密封面积，使密封失效。

2 试验验证

为验证有限元分析的结果，通过机械密封试验台进行试验。该试验台可以控制密封腔体的温度、压力及电机的转速，通过扭矩传感器ZH07-100T对机械密封的扭矩进行测量，该传感器精度为0.3%(对满量程)，试验台型号为STEFP-120；电机功率为30 kW；转速为0～6 000 r/min，轴径为25～120 mm；装置最大承受压力为4 MPa；承受最高温度为200 ℃。试验中仅对固有频率为18.839 Hz的动环第1阶模态进行验证。

2.1 试验方法

以工作介质为水的浓缩循环泵用机械密封进行试验分析。该机械密封动环和静环材料均为反应烧结碳化硅。密封面之间的摩擦因数理论值f=0.03，验证共振对机械密封摩擦因数的影响。ANSYS计算出的一阶固有频率18.839 Hz对应试验台电机转速1 500 r/min。取3组工作转速1 500 r/min(19 Hz)为A组，2 000 r/min(25 Hz)为B组，2 500 r/min(33 Hz)为C组，保持腔体温度恒定为30 ℃，腔体压力恒定为0.4 MPa，密封液压力恒定为0.6 MPa。

采A组进行磨损试验分析，试验时间为100 h。

2.2 摩擦试验结果

电机在3组不同转速下运行平稳后，通过扭矩传感器监测扭矩的变化。其扭矩变化如图3所示。

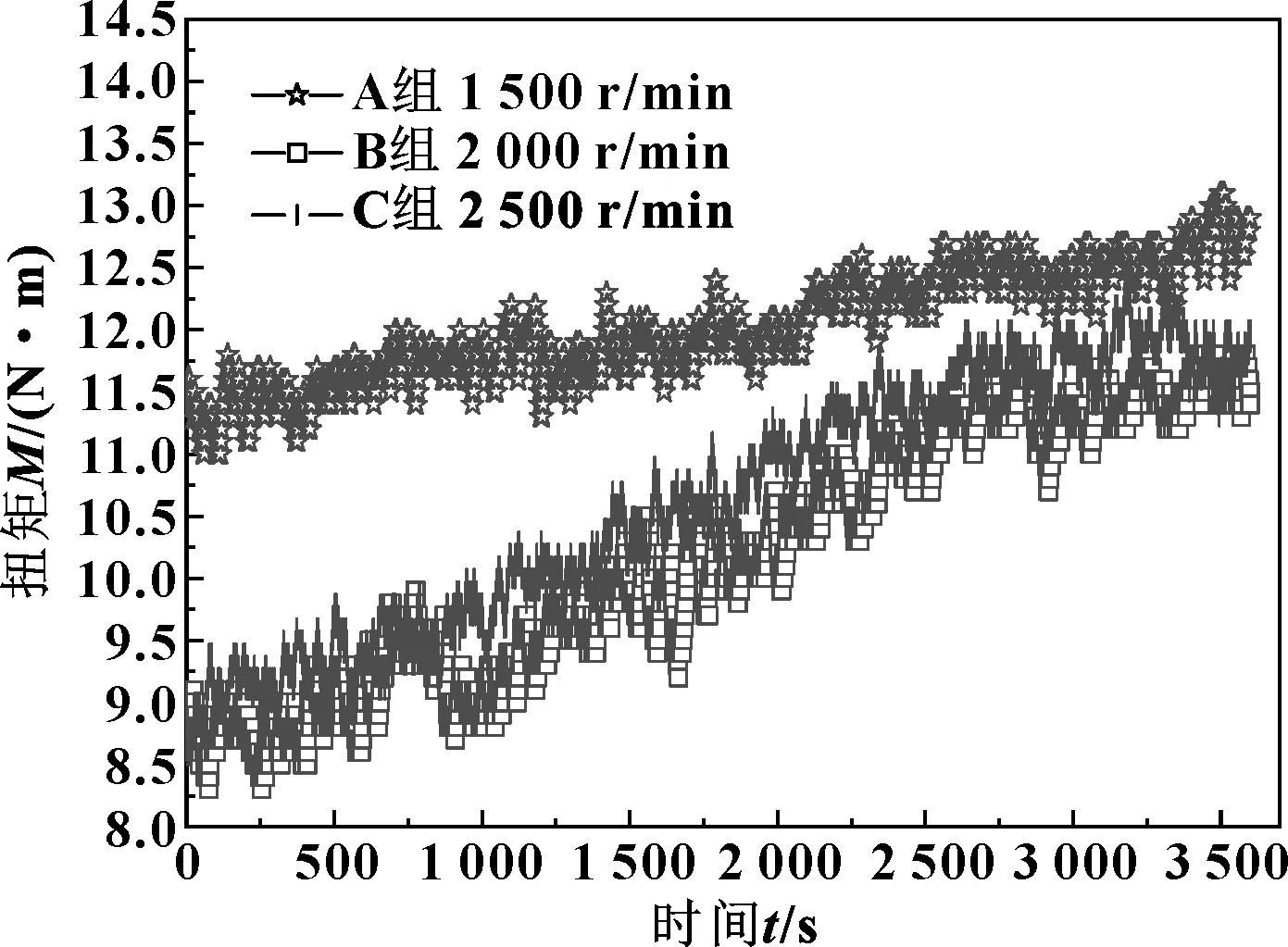
图3 不同转速下的扭矩变化Fig 3 Torque variation at different rotational speeds

从图3可见，当温度、压力保持不变的情况下，3组不同工作转速下的扭矩都先稳定增加后逐渐趋于平稳。这是因为，机械密封摩擦副之间充斥着薄厚不一的局部液膜，设备运行中其液膜厚度在端面扭转变形及摩擦的作用下越来越薄，导致扭矩升高，但一段时间后趋于稳定。A组转速下的扭矩从初始值开始就高于B、C组，且A组曲线斜率较小；B组和C组从同一起点开始，C组曲线略高于B组。

摩擦因数计算公式为

(10)

式中:p为端面平均水膜压力，MPa；rm为平均摩擦半径，mm；Mf为试验验装置总摩擦扭矩，N·m；M0为试验装置基准扭矩，N·m；Af为摩擦面面积，mm2。

由公式(10)可知，摩擦因数与扭矩成正比关系。因此，由图3中结果可得出A组的摩擦因数大于B组和C组。表3中给出了计算得到的实际摩擦因数和摩擦因数理论值。

表3 摩擦因数理论值和实际值

A组在1阶模态频率下，结构发生共振，使端面产生形变，增加了微凸体之间的接触面积，并增大相对滑动，导致扭矩高于其他2组，摩擦因数也高于理论值。在B组和C组的转速下，结构没有产生共振，扭矩相对A组较小，摩擦因数低于理论值。

2.3 磨损试验结果

磨损试验前，在动环上随机取Ⅰ点、Ⅱ点、Ⅲ点3个点，静环上随机取A点、B点、C点3个点。试验结束后将动环和静环分别拍照放大50倍进行对比分析，如图4所示。可知，动环密封面的主要磨损和划痕集中在外径处，3个点磨损面的大小和深度均不相同，并存在径向和切向的划痕，外径处局部出现破损，见I点。用棉球蘸乙醇溶液擦拭密封面，擦拭外径处的棉球变黑，擦拭内径处的棉球略有变化。静环与轴配合没有相对转动，静环的密封面磨损量比较小，均匀地分布在外径处，局部出现划痕，见图4(d)。

图4 机械密封局部磨损Fig 4 Local wear of mechanical seal (a)point Ⅰ of movable ring;(b)point Ⅱ of movable ring;(c)point Ⅲ of movable ring;(d)point A of static ring;(e) point B of static ring;(f)point C of static ring

振动导致的动环不仅有径向的相对扭动也有径向的相对滑动，产生的不规则磨损面导致动环外径处的端面十分粗糙，并且外径比内径的磨损严重。静环受振动的影响较小，静环端面磨损较少。长时间运转下粗糙的动环密封面会加大对静环的犁削作用，产生划痕如图4(d)所示。微凸体的之间通过弹性、塑性或弹塑性形变形成的黏着点被剪断，结焦在密封面上成为杂质，使得磨损愈加剧烈，使密封失效，降低了设备的使用寿命。

试验结果与有限元分析结果是一致的，验证了有限元分析的正确性。

3 结论

(1)通过对机械密封动环的有限元分析，得到其前10阶的模态振型的固有频率和应变关系。结果表明，机械密封的动环主要振型有径向产生相对扭转、两边向圆心方向发生弯曲、密封面沿径向摆动、端面产生相对拉伸、端面处整体产生很大的形变，动环应变随着固有频率的增加而增大。

(2)通过动环第一阶模态频率下的密封试验，发现当电机的工作频率达到动环的固有频率时，设备发生共振，在共振频率下其摩擦因数和力矩均有较大的增加。

(3)通过动环第一阶模态频率下的磨损试验，发现共振导致的动环扭转变形会造成密封面的局部磨损，使有效密封面积减小，从而使密封失效。在机械密封设计中应该避免振动造成的影响，使工作频率远离共振频率。