油气两相动压密封自振稳定性流固热耦合分析*

李双喜 廖浩然 陈 炼 刘兴华 赵 祥

(北京化工大学机电工程学院 北京 100029)

油气润滑是指通过压缩空气携带微量润滑油进行润滑的润滑方式[1]，其能够同时起到冷却与润滑的作用。油气润滑状态下的润滑油始终为液态，对坏境污染小[2]，因而广泛应用于轴承腔、齿轮箱的润滑。

油气两相动压密封是一种密封介质为油气混合物的密封装置，是航空航天等领域高速轴承箱的关键元件。密封自振是密封在运行过程中受到干扰并恢复后，补偿环在平衡位置发生的后续振动。一般用密封自振稳定性来表征密封发生自振的难易程度，自振稳定性包括轴向和角向的自振稳定性。密封自振稳定性较差时容易引发密封系统失稳，造成严重的后果，因此保证密封自振稳定性是密封长久稳定运行的必要条件。

油气两相动压密封作为非接触密封，具有使用寿命长、维护成本低、泄漏量小的特点[3]，且其稳定性以及密封性能优良。现有动压密封集中于有关槽型的优化[4-5]和温度场[6-7]的分析。在动态性能研究方面，邓强国等[8]、张伟政等[9]总结了流体动压干气密封研究现状，提出了微扰法、摄动法、龙格-库塔法、步进法等多种研究求解方法；李双喜等[10]求解了动静压密封端面间气膜雷诺方程；GREEN和BARNSBY[11]推导得到了非接触式气密封动态稳定性数值分析方法。

在自振稳定性研究方面，刘雨川等[12]提出了角向气锤自振概念，研究了不同端面结构对密封稳定性的影响；马纲等人[13]应用简正模验证了角向气锤振动的存在并总结了其对密封的影响；徐万孚等[14]研究了气膜密封轴向、角向刚度对自振稳定性的影响，总结了刚度与自振稳定性的关系；张树强等[15]研究了动静压混合式气体密封的自由振动临界失稳条件。

现有研究多集中于单相自振稳定性能研究以及油气两相流体性质的相关研究，缺少考虑热与变形下油气两相流体密封自振稳定性的研究。本文作者基于前人对油气润滑机制、动压密封性能、自振稳定性的研究，修正气体雷诺方程，采用流固热耦合数值分析方法，分析在油气两相工况下螺旋槽动压密封的动态性能，得到油气比、转速、压差和O形圈阻尼等参数对密封自振稳定性的影响。

1 油气两相动压密封结构与工作原理

1.1 密封结构

油气两相密封示意图如图1所示，密封端面外径侧与轴承相邻，工作时由喷油嘴喷出两相润滑介质润滑轴承，腔内循环气体，一般将轴承腔内介质视为分布均匀的油气两相润滑介质。油气两相密封组件由动环和静环组件两部分组成，动环随轴旋转，静环组件固定在腔体上，动静环的接触面称为密封端面。静环组件包括静环、O形圈、弹簧垫、波形弹簧和弹簧座。

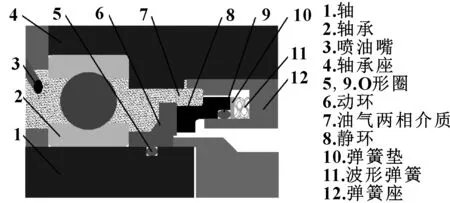
图1 油气两相动压密封示意Fig 1 Schematic of oil-gas two-phase dynamic pressure sealing

1.2 工作原理

油气两相密封静止时由波形弹簧提供闭合力，将静环紧紧贴在动环上，起到密封效果。在高速运转时，油气两相流体进入流体动压槽，产生一层具有一定刚度的流体膜，在推开动静环的同时密封住油气两相介质，达到无摩擦磨损、零泄漏甚至倒吸的效果。其动力学模型如图2所示。

图2 密封原理Fig 2 Sealing principle

1.3 密封参数

动环端面螺旋槽尺寸对运转形成流体膜的刚度以及旋转时流体膜厚度的影响很大。油气两相动压密封端面结构参数包括外径、内径、螺旋槽外径、螺旋角、槽深、槽坝比、槽宽比、槽数端面结构示意图如图3所示。

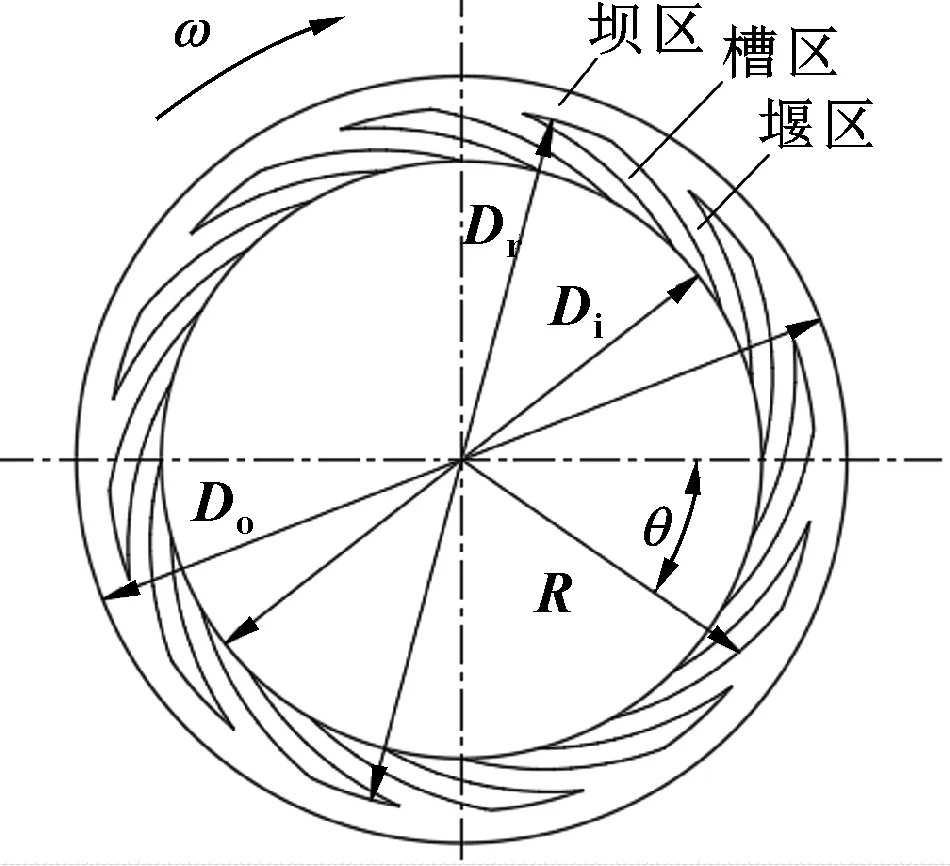
图3 端面结构示意Fig 3 Schematic of the end face structure

文中针对某轴承箱油气两相动压密封的结构展开分析，端面尺寸[16]如表1所示。润滑油和空气的物性参数如表2所示，密封分析参数如表3所示。

表1 端面结构尺寸

表2 密封介质物理性质

表3 密封分析参数

2 油气两相动压密封自振稳定性数学模型

2.1 动态分析模型

以动环端面中心为原点建立坐标系，油气两相动压密封动力学模型如图4所示。补偿环静环初始平衡位置为ho处，在密封受到来自外界的扰动时，静环会沿z轴方向发生轴向振动、绕x轴和y轴发生角向振动，振动方向的密封动静环旋转为周期运动，假设图5中补偿环静环的微扰运动定义为简谐运动，z(t)、α(t)、β(t) 3个方向运动方程如式(1)所示。经过推导获得动压密封18个动态性能的表达式[17],如式(2)所示。

(1)

式中：t为时间；i为虚数单位；ν为补偿环受到微扰的频率。

(2)

式中：kmn、cmn(m,n=z,x,y)代表油气两相介质流体膜的动态性能参数；pzr、pαr、pβr、pzi、pαi、pβi参数计算如式(3)所示。

(3)

其中p的计算公式如式(4)所示。

(4)

利用MatLab求解式(2)，获得油气两相动压密封动态性能参数。Δz、Δα和Δβ定义如图4所示。

图4 油气两相动压密封动力学模型Fig 4 Oil-gas two-phase dynamic pressure sealing dynamic model

2.2 自振稳定性分析模型

补偿环的振动分为轴向自振和角向自振。轴向可将动压密封补偿环视为一个弹簧-阻尼系统,如图5所示。当非补偿环受到微小扰动，补偿环系统将产生自振。

图5 分析模型示意Fig 5 Schematic of the analysis model

2.2.1 轴向自振运动方程

轴向自振方程表达式为

(5)

令c=(czz+cs)，k=(kzz+ks)，则有：

(6)

设ω0为系统固有频率；δ为阻尼系数；ζ表示阻尼比，有：

(7)

阻尼比ζ<1、ζ=1、ζ>1时振动方程不同，在阻尼比ζ≥ 1的情况下，补偿环的运动会逐渐衰减，此时由于阻尼的作用，补偿环的自振随着时间而减小，故在此种情况下，补偿环系统不会发生失稳。在阻尼系数ζ<1时，为欠阻尼状态，其振动方程如式(8)所示。

z=e-δt[C1cos(ωdt)+C2sin(ωdt)]

(8)

在ζ<1时，补偿环运动因为阻尼系数δ的取值分为以下3种情况，同时据式(8)可知：

(1)δ<0：此时-δt>0，即补偿环的振幅随着时间t的增加而递增，最终导致系统失稳。

(2)δ>0：此时-δt<0，即补偿环的振幅随着时间t的增加而减少，最终保持系统稳定。

(3)δ=0：此时-δt=0，即系统振幅变化为三角函数，补偿环简谐振动。

由分析可以看出，在δ=0时为系统长期运行失稳或稳定的临界判断点。取此时的系统频率以及质量为临界频率和临界质量。

设δ=0，此时的振动方程如式(9)所示。

z=eiυcrt

(9)

式中：υcr为密封的临界频率。将式(9)代入式(6)得：

(10)

当虚部等于0时计算临界频率：

c=czz+cs=0

(11)

实部相等计算临界质量：

(12)

因此，油气两相动压密封轴向自振稳定性判据为

(13)

式中：υzcr表示轴向临界转动频率。

即在满足式(13)条件下补偿环保持轴向自振稳定。

2.2.2 角向自振运动方程

角向自振运动方程为

(14)

式中：Ix=Iy=I;ksx和ksy为角向刚度，csx和csy为辅助O形圈的角向阻尼，可由式(15)[18]计算得到。

(15)

设α=C1ert，β=C2ert，其中r=λ+iυ。将式(15)代入式(14)，当C1、C2存在非零解时：

a0+a1r+a2r2+a3r3+a4r4=0

(16)

式中：

(17)

λ=0时为密封的临界失稳状态，则有

r=iυcr

(18)

可得到密封角向自由振动临界转动惯量为

(19)

式中:keq为角向自振恢复力矩等效刚度,其计算式为

(20)

因此，油气两相动压密封角向自振稳定性判据为

(21)

式中：υωcr表示角向临界转动频率。

即在满足式(21)条件下补偿环保持角向自振稳定。

2.3 油气两相雷诺方程

假设油气两相介质中油滴与空气混合均匀，油滴之间相互独立，不会相互影响。将密封端面间的流场单元化，其单元物理模型[19]如图6所示

图6 密封端面间油气两相流体的物理模型Fig 6 Physical model of oil-gas two-phase fluid between sealed end faces

油气比c0即为油滴在两相介质中所占的体积比，膜厚h为密封端面间流体膜厚。经过推导得到修正黏度μm计算公式如式(22)所示[20]。

(22)

实际情况中黏度随温度、压力变化较小，为了方便计算，假设黏度为常数。

油气两相流体的等效密度ρm为

ρm=ρliqco+ρgas(1-c0)

(23)

式中：ρliq、ρgas分别为液体和气体密度。

综上得到用于求解油气两相密封端面流体膜压力分布的修正压力控制方程(Reynolds方程)如公式(24)所示。

(24)

式中：rL、θ分别为所研究流域极坐标中的长度与角度。

通过求解油气两相动压密封稳态方程与流固热耦合计算，求流体膜端面压力分布，如图7所示。

图7 油气两相流体膜压力分布云图Fig 7 Oil-gas two-phase fluid membrane pressure distribution contour

再通过求解动态性能的油气两相动压密封非稳态雷诺方程获得动态性能参数，进而求解临界频率、临界质量、临界转动惯量，分析补偿环自振稳定性。

2.4 流固热耦合计算模型

流固热耦合分为固体域计算、流体域计算、热计算3部分，在动静环推开以后，端面形成1～4 μm厚的流体膜。密封端面变形会影响流体膜的厚度以及流体膜的压力分布，从而影响开启性能。运行过程中密封受热产生热变形，进而影响端面变形以及膜压。此三者之间相互影响形成一个稳定的状态，其流固热耦合流程图如图8所示。密封端面的微小变形对摩擦生热影响不大，此处只考虑温度对密封环变形的单向影响。具体计算方法如下：

图8 流固热耦合分析流程Fig 8 Flow of fluid-solid-thermal coupling analysis

(1)根据实际结构对密封环进行建模并划分网格，其静环网格如图9所示，计算求出密封环的变形矩阵。利用密封环变形分量δij和δid修正流体膜初始厚度，即hi=ho+δij+δid，所得到的hi即为流体域计算初始厚度修正值。

图9 静环网格Fig 9 Static ring grid

(2)根据热计算过程得到密封环在环境温度和黏性剪切热下的热变形δkj和δkd，再一次对膜厚初始值进行修正，即得到流体域计算初始值。

(3)进行流体域部分计算，得到流体膜部分的压力分布p1，将压力作为边界条件重新进行固体域计算，得到密封环的变形δ′ij和δ′id。新的流体膜膜厚为h′i=ho+δ′ij+δ′id+δkj+δkd，将新的流体膜膜厚h′i代入流体域进行计算，设定压差精度(ε)进行迭代计算。当压差在精度范围内，则视为流体膜压力分布、密封环变形达到稳态，完成流固热三大部分的耦合。

2.5 计算模型准确性验证

Λ是压缩数，其表达式为

(25)

压缩数对临界频率比影响如图10所示。文中所用油气两相动压密封数学模型计算所得结果与文献[20]中结果趋势相似且数值差距较小，验证了数学模型的正确性。

图10 临界频率计算结果的对比验证Fig 10 Comparison of calculation results of critical frequency ratio

临界频率、临界质量和临界转动惯量是自振稳定性的表征参数，在密封运行过程中油气比、转速、压差和O形圈阻尼等参数的变化可能会引起机械密封自振。分析机械密封运行过程中油气比、转速、压差和O形圈阻尼等参数对临界频率和临界质量的影响，对密封自振稳定性设计有指导性意义。

3 结果及分析

3.1 油气比对密封自振稳定动态特性的影响

油气比对密封自振稳定动态特性的影响如图11所示，图中耦合前后油气比对轴向临界频率、轴向临界质量、角向临界频率和角向临界转动惯量的影响趋势相同，说明流固热耦合前后流体进出端面的微流动机制相同。耦合产生的变形对局部流体以及性能产生了影响，导致4个表征参数不同。如图11(a)所示，油气比小于0.1前耦合后两相介质临界频率较大，而油气比大于0.1时相反。这是由于气相可压缩性强，对耦合产生的变形敏感进而对轴向临界频率的影响较大。

如图11(a)、(b)所示，轴向临界频率随着油气比的增加而减小，轴向临界质量随着油气比的增加而增加，在油气比c0为0.1～0.15时，轴向临界频率以及轴向临界质量相对较大。如图11(c)、(d)所示，油气比c0为0.15左右时角向临界频率和角向临界转动惯量相对较大。综合考虑油气比对各表征参数的影响，油气比c0在0.1～0.15时，油气两相动压密封自振稳定性较好。

3.2 转速对密封自振稳定动态特性的影响

转速对密封自振稳定动态特性的影响如图12所示，耦合前后纯气相以及耦合前后油气两相的轴向临界频率、轴向临界质量、角向临界频率以及角向临界转动惯量在转速变化下的变化趋势大致相同。耦合后的纯气相介质以及油气两相介质轴向临界频率、角向临界转动惯量大于未耦合的情况，而轴向临界质量与角向临界频率与耦合后介质的变化规律则相反。这是由于压力以及温度的作用使得端面产生一定的发散锥度，使得轴向接触面积减小，轴向临界频率减小；产生的角向阻力减小，角向临界频率增加。

如图12(a)、图12(b)所示，轴向临界频率和轴向临界质量随着转速提升而减小，同时变化速率减小，这是由于转速增加，螺旋槽产生动压效果使得开启力增加，轴向自振稳定性变差。如图12(c)、图12(d)所示，角向临界频率随着转速提升而平稳增加，角向临界转动惯量则相反。这是由于转速增加使得端面间油气两相介质分布更加均匀，设计油气两相动压密封中应在实际转速下综合考虑4种参数的大小，规避失稳。

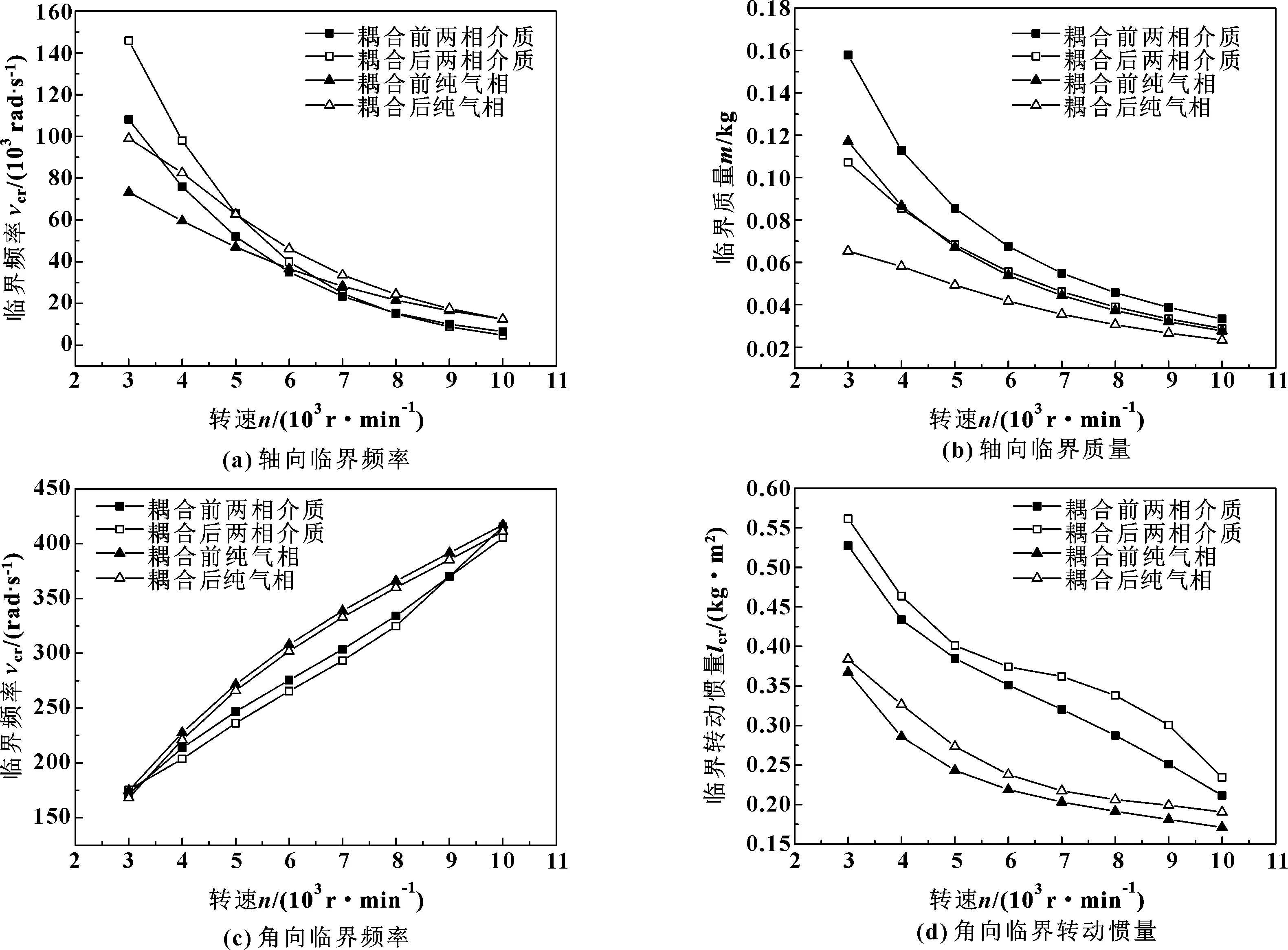
图12 转速对密封自振稳定动态特性的影响Fig 12 Effect of rotational speed on the self-vibration stability of the seal (a)axial critical frequency;(b)axial critical mass; (c)angular critical frequency;(d)angular critical moment of inertia

3.3 压差对密封自振稳定动态特性的影响

如图13(a)所示，压差增大虽然使得端面间开启力增加，但在载荷系数较大的情况下，压差增大使得端面闭合力增加，因此轴向临界频率随着压差的增加而增大且变化趋势加大。

如图13(b)所示，轴向临界质量在压差变化的情况下基本保持不变。即在补偿环质量小于轴向临界质量的条件下，压差增大能够增大密封轴向自振稳定性。如图13(c)所示，由于压差增大使得径向流体膜压力分布跨度增大，不利于角向自振稳定性，角向临界频率随着压差的提升而减小。如图13(d)所示，临界转动惯量随着转速的提升而增大。这是由于压差增加导致轴向闭合力增加，轴向稳定性更好，同时角向条件更加苛刻，容易受到干扰发生失稳。

图13 压差对密封自振稳定动态特性的影响Fig 13 Effect of differential pressure on the self-vibration stability of the seal (a)axial critical frequency;(b)axial critical mass; (c)angular critical frequency;(d)angular critical moment of inertia

3.4 O形圈阻尼对密封自振稳定动态特性的影响

如图14(a)所示，轴向临界频率随着O形圈阻尼增加而增大，耦合前后介质情况下计算的轴向临界频率差别不大。如图14(b)所示，O形圈阻尼的变化对临界质量的大小基本没有影响。从图14(c)可以看出，O形圈阻尼的变化对油气两相介质角向临界频率的影响比纯气相时大。从图14(d)可以看出，耦合后介质情况下计算的角向临界转动惯量，受O形圈阻尼变化影响较大，这是由于端面变形产生的锥度，对临界转动惯量计算影响较大。

图14 O形圈阻尼对密封自振稳定动态特性的影响Fig 14 Effect of O-ring damping on the self-vibration stability of the seal (a)axial critical frequency;(b)axial critical mass; (c)angular critical frequency;(d)angular critical moment of inertia

4 结论

(1)油气两相动压密封轴向临界频率随着油气比增大而减小，轴向临界质量随着油气比的增大而增大，油气比在0.1～0.15时油气两相动压密封自振稳定性较好，在补偿环质量较大时易选择大油气比环境。

(2)转速较低时轴向自振稳定性较好而角向自振稳定性较差，转速高时两者相反，即在极端转速情况下油气两相动压密封自振稳定性较差。

(3)在满足临界质量要求情况下，压差越大轴向自振稳定性越好，角向自振稳定性较差。压差达到一定程度后，角向自振稳定性随压差增大而不再减小，趋于稳定。低压差设计时应着重考虑轴向自振稳定性，高压差则相反。

(4)O形圈阻尼较低时轴向自振稳定性较差而角向自振稳定性较好，O形圈阻尼高时两者相反，即在取极端O形圈阻尼时，油气两相动压密封自振稳定性较差。由于轴向临界频率整体较大，在角向自振稳定性较差时易选用较大阻尼O形圈。