旋转分数阶Fourier域构建SAR方位向成像算法的研究

王振力，王群，陈先意，马如坡，刘晓迁

(1.江苏警官学院 计算机信息与网络安全系，南京 210031；2.南京信息工程大学 计算机与软件学院，南京 210044)

0 引言

合成孔径雷达(synthetic aperture radar，SAR)具有不受光照和气候条件等限制实现全天时、全天候对地观测的特点，可穿透地表或植被获取其掩盖的信息，在民用和军事领域具有广阔的应用前景。SAR通过把小孔径天线雷达装载在运动的载体上，利用雷达与地面测绘带内各种目标的相对运动进而利用相干处理实现距离向和方位向成像[1]。常见的SAR成像算法[2]主要有距离多普勒(range Doppler，RD)算法、波数域(ωK)算法和CS(chirp scaling)算法等，其中距离多普勒算法[3-4]是SAR成像处理中最常见、最经典的方法。目前距离多普勒算法虽然在许多模式的SAR尤其是正侧视SAR成像处理中仍然广为使用，但是其较低质量的图像越来越不能满足实际应用需求[5-6]。

众所周知，Fourier变换在传统距离多普勒算法成像处理中起着至关重要的作用，而同时Fourier变换也是分数阶Fourier变换(fractional Fourier transform，FrFT)阶数为1时的特例。分数阶Fourier变换是一种广义的Fourier变换，它是一种统一的时频变换，随着变换阶数从0连续增长到1而展示出信号从时域逐步变化到频域的所有特征。将分数阶Fourier变换应用于SAR成像处理是近年来的研究热点[7-14]。文献[7-8]针对线性调频(linear frequency modulation，LFM)信号的参数估计问题,提出在分数阶Fourier域进行二维谱峰搜索来确定分数阶Fourier变换的最佳变换阶数，该方法稳定性较好但搜索分数阶谱峰计算量大，同时有限数据样本会导致参数估计精度的降低。Capus 等[9]利用几何变换关系得到适用于线性调频信号的分数阶Fourier变换[10]最优变换阶数，但相应的分数阶Fourier变换无法代替传统距离多普勒算法中的Fourier变换进而实现信号重构。Mashed等[11]将分数阶Fourier变换应用于传统的RD算法，虽然可获得SAR成像性能的提高，但同时计算复杂度也相应增加。陈勇等[12]通过局部最优处理来测量SAR回波信号的调频率并以此计算FrFT的最优阶数，所研究算法在提高弹载SAR成像性能方面是有效的但不具有适用的普遍性。为获得地面运动目标清晰的SAR图像，Tan等[13]提出分数阶Fourier变换与自适应迭代模糊数算法相结合的多普勒参数估计方法；Wang等[14]提出联合利用Wigner-Ville 分布和分数阶Fourier变换实时估计多普勒参数的方法，并且观测信号的WVD处理决定分数阶Fourier变换的旋转角；Huang等[15]利用距离-频率变量的等间隔采样，研究了基于RFRT-FrFT的合成孔径雷达地面运动目标成像新算法。

本文针对传统距离多普勒算法方位向成像质量低的问题，首先对SAR方位向信号进行变换分析得到其阶数表达式；接着构建旋转分数阶Fourier变换域和方位向高分辨率成像算法；最后给出模拟数据和实测数据实验结果与分析。

1 SAR方位向信号变换分析

在SAR成像系统中，理想的点目标回波在方位向近似为线性调频信号的形式，如式(1)所示。

sa(t)=Wa(t)exp(j2πfdct+jπκat2)

(1)

式中：fdc为多普勒中心频率；κa为方位向调频率；Wa(t)=rect(t/Ta)；Ta为合成孔径时间。连续信号f(x)的分数阶Fourier变换定义式如式(2)所示。

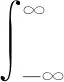
(2)

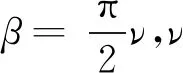
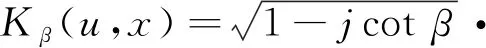
(3)

将式(1)代入式(2)，得到式(4)。

(4)

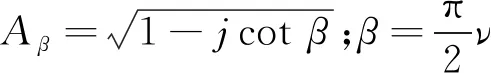
经简化计算并利用驻定相位定理(principal of stationary phase)[16]，可得SAR回波方位向信号进行分数阶Fourier变换时的最优阶数，如式(5)所示。

(5)

式中：arctan(·)为反正切函数；Na为抽样序列长度；Fa为抽样频率。对于实际SAR数据成像，Na长度既不可过大，也不可过小，否则会影响方位向成像质量，即方位向分辨率、方位向峰值旁瓣比(peak side lobe ratio，PSLR)和方位向积分旁瓣比(integrated side lobe ratio，ISLR)会受到相应的影响。

2 旋转分数阶Fourier变换域的构建

对于给定的SAR回波抽样信号，方位向调频率κa、抽样序列长度Na和抽样频率Fa均是已知的，因此根据式(5)可直接计算出相应的最优阶数νopt，相对应的时频域旋转角为β=-νopt×π/2。如图1所示，其中负号表示逆时针旋转，tν和fν分别表示方位向时间域和方位向频率域。图1中，yβ表示对方位向时域信号作旋转角为β时的FrFT相对应的分数阶Fourier变换域；yβ ′表示对分数阶Fourier变换域yβ中信号作旋转角为β′(β′=π/2，对应阶数为1)时的FrFT相对应的分数阶Fourier变换域;t′ν表示tν的平行轴，显然tν⊥fν，yβ⊥yβ ′，方位向回波信号在时频域(tν，fν)中分解形式与其在分数阶Fourier变换域(yβ，yβ ′)中的分解形式是等价的，且后者更利于方位向回波信号能量的聚焦。若yβ域中分解信号等同于fν域中的频率信号，则yβ ′域中分解信号等同于tν域中的时间信号。

图1 方位向信号时频域旋转图

3 方位向高分辨率成像算法的构建

无论机载或星载SAR成像，为提高方位向信号在分数阶Fourier变换域中的成像聚焦效果，可将相应的时频角旋转π/2变换至(yβ ′，yβ ″)，此时方位向最优阶数变为ν′opt=1-νopt，如图2所示。图2给出了以传统距离多普勒算法为基础的方位向成像算法的构建流程图。由于多普勒中心频率fdc在SAR正侧成像模式下其值为0，式(5)是在此条件下得出的结论，因此依据此结论构建的算法与传统距离多普勒算法的适用条件是一致的，即适用正侧模式成像。

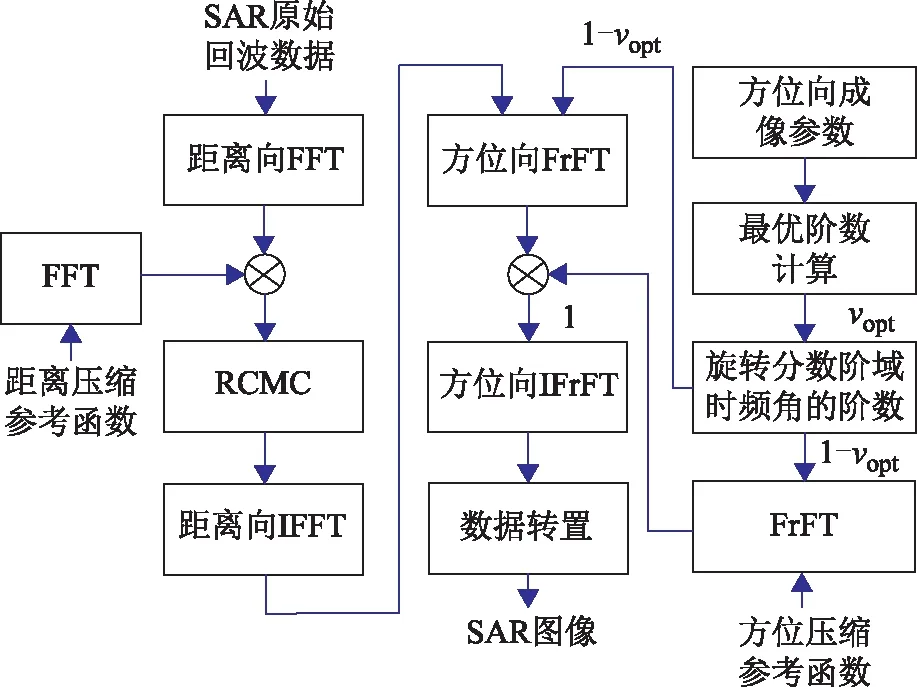
图2 方位向高分辨率成像算法的构建流程图

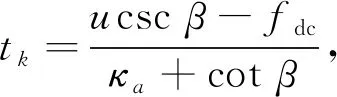
无论fdc是否等于0即正侧模式还是斜侧模式(小斜视角)成像，其对SAR成像精度均无影响，前提是fdc估计数值不能存在误差。如果其数值存在误差，方位匹配滤波器的中心频率会偏离频谱能量峰值，这会导致多普勒频谱混叠最终出现图像模糊。因此，本文算法也可适用于小斜视角条件下成像模式，这与传统距离多普勒算法也是一致的。

4 数据成像实验及分析

机载SAR正侧视点目标成像仿真参数为：载波频率为4 GHz，信号带宽为120 MHz，信号脉宽为5 μs，信号抽样频率为192 MHz，脉冲重复频率(PRF)为154 Hz，方位向天线尺寸为3 m，载机飞行速度为154 m/s，中心点斜距为5 000 m。仿真实验中所选PRF的方位向过抽样率系数为1.5，3个点目标幅度系数分别为0.8、1和1.2。对于采用传统的RD算法、本文算法的3个点目标成像，由表1数据可知，在PSLR和ISLR相当的情况下，本文算法获得的方位向分辨率绝对值降低0.42，相应的分辨率提高比值为31.3%。本文算法的方位向高分辨率成像在图3和图4中也能得到明显体现。图3所示的插值后点目标成像轮廓图表明，经本文算法成像得到的点目标其方位向主瓣能量聚焦性能更优，相应的旁瓣能量明显减弱。图4 所示的插值后峰值点目标成像剖面图表明，经本文算法成像的点目标其方位向波形主瓣宽度明显变窄，旁(副)瓣电平也相应降低，因而其成像的清晰度得到显著提高。

表1 方位向成像性能对比

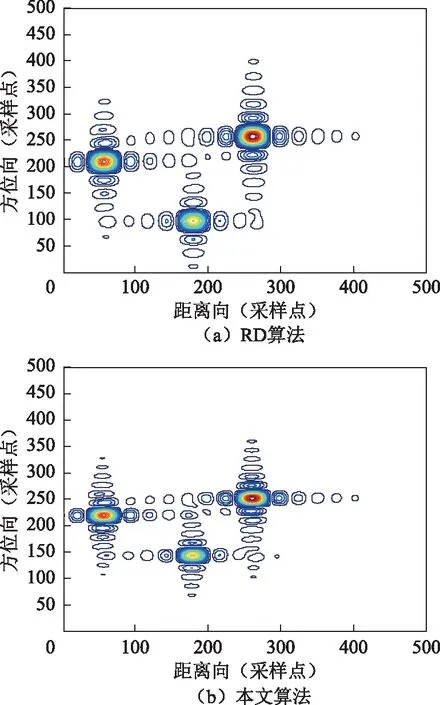
图3 插值后点目标的轮廓图

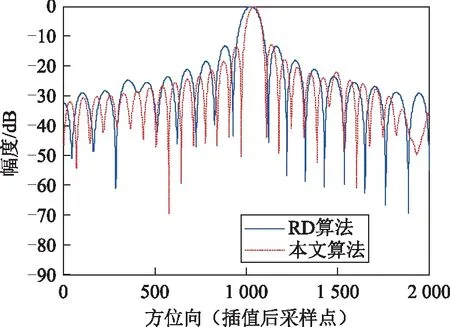
图4 插值后峰值点目标成像方位向剖面图

图5给出了星载SAR实测数据成像结果，其原始数据来自于加拿大Radarsat-1精细模式下温哥华场景(截取)。图5成像结果表明：与传统RD算法相比，经本文算法得到的SAR图像分辨率高，所获得的图像中自然景观公园、马路和高速公路等清晰可见，斑点噪声小，纹理和边界线明显，强点目标突出，强弱目标对比度高。图6和图7分别给出了与图5相对应插值后的峰值点目标成像轮廓图、峰值点目标成像方位向剖面图，表2给出了方位向成像性能对比。由图6和图7可知，由本文算法成像的峰值点目标方位向主瓣宽度明显变窄，旁瓣电平明显降低，尤其是第一旁瓣能量显著降低。由表2中实验结果可知，在PSLR和ISLR相当的情况下，本文算法成像方位向分辨率绝对值比传统RD算法降低12.12，相应的方位向分辨率提高比值为41.8%。

图5 SAR实测数据成像

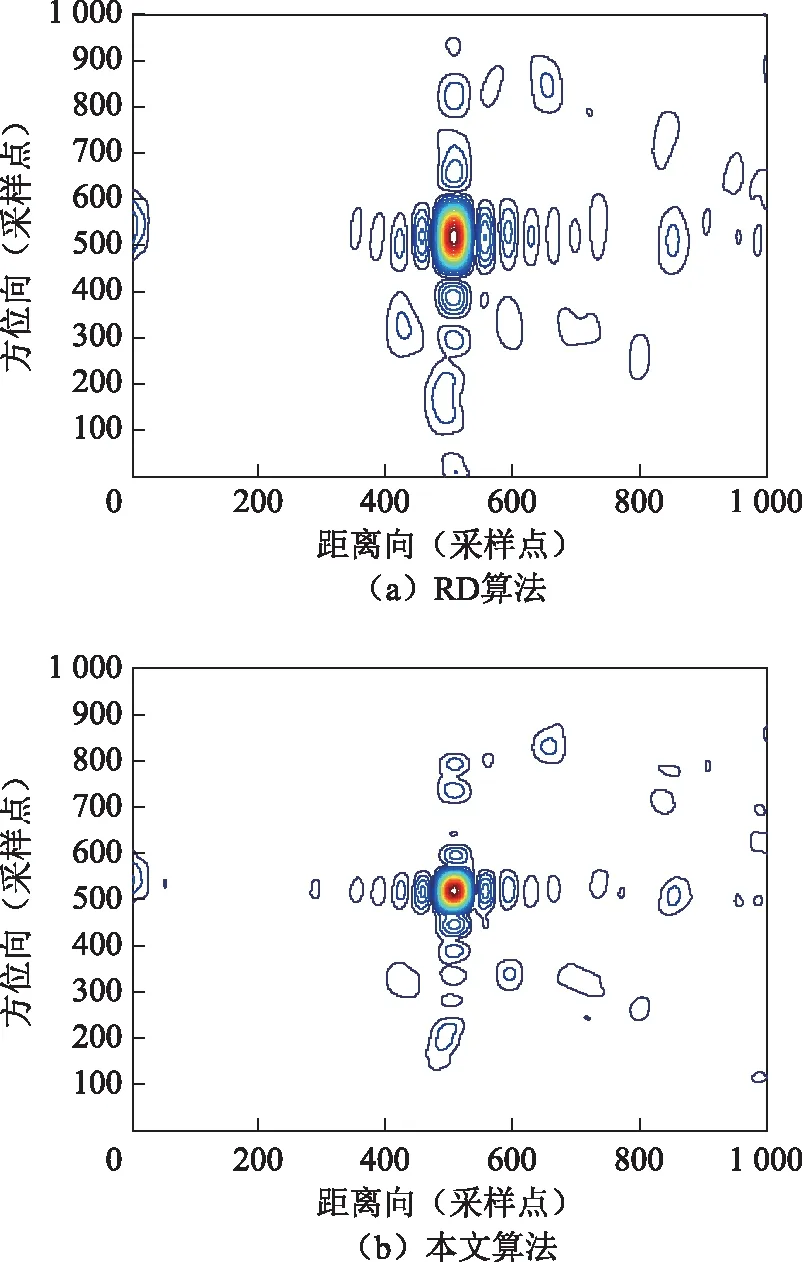
图6 插值后峰值点目标成像轮廓图

图7 插值后峰值点目标成像方位向剖面图

表2 方位向成像性能对比

以上机载SAR仿真数据和星载SAR实测数据成像实验表明，由本文算法得到的SAR图像均可获得比传统RD算法更优异的成像性能，这主要是因为本文算法在方位向依据最优阶数获得的旋转分数阶Fourier变换域(y′β1，yβ2)具有比传统Fourier域更好的目标成像聚焦效果。

5 结束语

本文通过分数阶Fourier变换的阶数分析，建立SAR成像方位向最优阶数计算表达式；以传统的距离多普勒算法为原型，基于方位向最优阶数获得旋转分数阶Fourier变换域并提出方位向高分辨率SAR成像算法。机载SAR模拟数据和星载SAR实测数据成像结果表明，在峰值旁瓣比和积分旁瓣比相当的情况下，与传统距离多普勒算法相比，本文算法得到的SAR图像在方位向上的分辨率得到显著提高，同时本文算法具有图像斑点噪声小、图像纹理清晰和强弱目标对比度高等优点，因此更有利于SAR图像目标的特征提取、目标识别、判读与解译。传统的距离多普勒算法在方位向可看作本文算法的特例，二者计算量相当。本文算法的执行无需额外增加SAR载体平台的任何硬件成本，具有良好的推广应用价值。