离子晶体中熵的性质

李越,任恒峰,王清亮

(忻州师范学院 物理系,山西 忻州 034000)

离子晶体是由正负离子或正负离子集团按一定比例、通过离子键结合而成的晶体[1-3],它是固体物理学理论中一种基本的、典型的模型,在理论上和实际中都具有非常广泛的应用[3,4].自然界中最常见的离子晶体有强碱、活泼金属氧化物、大部分盐类等晶体,日常生活中经常遇到的NaCl晶体即为一种典型的离子晶体.目前,随着科学技术的日益进步,和对其他重要物理规律的研究一样,对于离子晶体的研究也已取得了长足的发展[5-10].然而,尽管很多工作对离子晶体的某些热力学特征量做了较为细致的研究,但对于其熵的研究仍然不够深入.在此基础上,本文主要讨论离子晶体的熵,并给出一种熵函数相应的计算方法.

1 晶格量子热容

在晶格热容的发展中,德拜对晶格采取了一个简单的近似模型[3],他认为如果不从原子理论而纯粹的从宏观的角度来看,可以把晶体视为各向同性的连续弹性介质,进而晶体振动的格波可看作是弹性波,并在此基础上引入了德拜模型的近似频率分布函数

(1)

据此,可直接写出晶体的量子热容

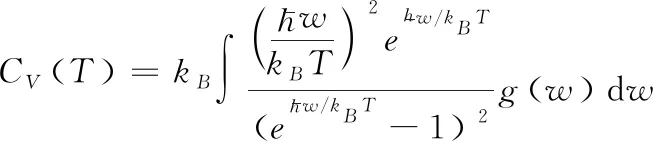
(2)

根据弹性理论,晶格振动频率w可取0到∞的任意值,对式(1)积分,将得到发散的结果,换句话说,振动模的数目或者晶体的自由度是无限的.对于连续介质而言,很自然的可以得到这样的结果,因为理想的连续介质包含无限的自由度；然而,如果考虑包含N个原子的晶体,其自由度则只有3N个.为了解决这一矛盾,德拜假设振动频率高于某一wm的短波实际不存在,而频率低于wm的振动都可用弹性波近似,则wm可由自由度来确定如下

(3)

即

(4)

(5)

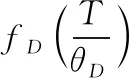
在高温极限下

(6)

代入式(5),可以得到

CV=3NkB

(7)

即,高温极限时与杜隆-珀替定律一致.

在低温极限下

(8)

代入式(5),可以得到

(9)

即,低温极限时,晶格量子热容与T3成正比,这个规律称为德拜T3定律.

2 离子晶体的熵

离子晶体可以视作是一个热力学系统,它的一切热力学变化(包括相变化和化学变化)方向和限度都可归结为热和功之间的相互转化及其转化限度的问题,热力学自发过程的方向和限度可以用一个普遍的热力学函数——熵函数来进行判别.熵函数既是一种状态函数,又是一个判别性函数(有符号差异),利用它能够定量地说明自发过程的趋势大小[5].

在物理学领域中,熵函数是一个非常重要的热力学状态函数,它的变化与中间途径没有关系,而只与始末状态有关.熵函数与能量的概念相类似,也是与某一状态所对应的函数,它是在热力学第二定律的基础上建立起来的.熵的大小可以反映系统所处状态的稳定情况,熵的变化指明热力学过程进行的方向,系统有趋向于最大混乱度的倾向,系统混乱度增大有利于反应自发地进行.根据统计物理学的观点,从微观上讲,熵与体系的混乱度有关,即它是体系混乱度的量度[6].熵可以用符号S来进行表示,若用Ω表示微观状态数,则熵可以定义为

S=klnΩ

(10)

其中,k=1.38×10-23J·K-1(k=R/NA),为玻耳兹曼(Boltzmann)常数.

选T、V为状态参量,由式

(11)

可得熵的全微分为

(12)

求线积分得

(13)

S0是初始条件下熵的值.离子晶体体系的晶格热容如式(5)所示,将其代入式(13)可得体系的熵函数表达式为

(14)

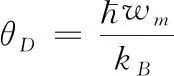
(15)

在低温极限下,将晶体体系的热容量式(9)代入可以得到低温极限的熵函数为

(16)

其中,R=NkB.

若选T、p为状态参量,则晶体状态方程为

V(T,p)=V0(T0,0)[1+α(T-T0)-κTp]

(17)

其中α为体胀系数,κT为等温压缩系数,对于简单离子晶体,α和κT的数值都很小,在一定的温度范围内可以把它们看作常数[10].引入符号V1=V0-αV0T0,则体系物态方程可表示为

V=V1+V0(αT-κTp)

(18)

由此可得

(19)

代入式(15)、(16)中,可以得到高温极限和低温极限下离子晶体的熵随温度T而变化的函数关系式分别为

(20)

(21)

3 结 论