500m 级双曲抛物面空间缆索人行悬索桥探讨
斯朗拥宗 扎西罗布
(1.西藏大学工学院 拉萨850012; 2.西藏自治区交通勘察设计研究院 拉萨850000)
引言
随着人行悬索桥的跨度不断增加, 其结构日趋轻柔化[1,2]。跨度大幅度增长带来的主要问题是悬索桥结构空间刚度的急剧下降, 竖向平行的缆索体系悬索桥对风荷载的作用非常敏感, 其抗风问题日益突出[3,4], 这使得风致振动对大跨径悬索桥安全性的影响更加重要, 而影响大跨径悬索桥风振性能最为关键的因素就是抗风稳定性。
现有人行景观悬索桥设计仍是依据传统的大跨径公路悬索桥设计理念, 缺乏创意, 其桥塔仍为传统的公路悬索桥门式桥塔结构, 美学效果不理想[5,6]; 同时, 随着跨径的发展, 亟需解决超大跨人行悬索桥的抗风稳定性问题[7,8]。
本文针对超大跨径人行景观悬索桥, 提出一种卵蛋拱形桥塔的双曲抛物面空间缆索体系大跨径人行悬索桥, 采用卵蛋拱形桥塔代替门式桥塔结构, 在卵蛋拱形桥塔之上悬挂碳纤维双曲抛物面空间缆索体系, 以便提高超大跨径人行悬索桥的空间刚度, 钢丝平行缆索和碳纤维双曲抛物面空间缆索两组缆索协同工作, 优势互补。
结合某500m 级超大跨径人行景观悬索桥,开展超大跨径双曲抛物面空间缆索体系人行悬索桥的结构构形研究, 进行工程参数设计, 建立Midas 有限元分析模型, 开展悬索桥的颤振稳定性分析研究, 从根本上解决特大跨人行悬索桥抗风稳定性问题。
1 构形研究
改革传统人行悬索桥结构, 采用卵蛋拱形桥塔代替门式桥塔结构, 卵蛋拱形桥塔由上部抛物线和左右椭圆弧线组成, 造型美丽, 可提升人行悬索桥的景观品位。改革传统人行悬索桥缆索,增加碳纤维双曲抛物面空间缆索, 形成平行钢丝缆索和碳纤维双曲抛物面空间缆索混合缆索, 碳纤维双曲抛物面空间缆索悬挂于卵蛋拱形桥塔的抛物线段拱圈上, 二组缆索混合使用, 优势互补, 协同工作, 可提高人行悬索桥结构抗风稳定性。在碳纤维双曲抛物面空间缆索上铺设不锈钢铁丝网, 种植藤蔓植物, 可遮蔽阳光, 同时增加景观效果。
双曲抛物面是一种高斯负曲面, 其曲面可由一条凸形抛物线在另一条凹形抛物线上移动而形成。同时双曲抛物面也是典型的二次直纹曲面,其曲面可以由两族直线构成, 应用直纹曲面建造的空间交叉杆系建筑物, 可形成空间扭壳结构,具有优良的力学性能。双曲抛物面方程为:

式中:fx、fy为双曲抛物面空间索网纵向和横向矢高;a、b为半长和半宽。
分析可得直纹线水平投影的斜率为:

双曲抛物面空间缆索按照抛物线线形下垂一定垂度, 平行主缆和碳纤维双曲抛物面空间缆索形成混合缆索结构体系, 平行缆索用以承担竖向荷载, 双曲抛物面空间缆索用以提高悬索桥的抗侧刚度和抗扭刚度, 两组缆索协同工作, 优势互补。双曲抛物面空间缆索分布形式如图1 所示。
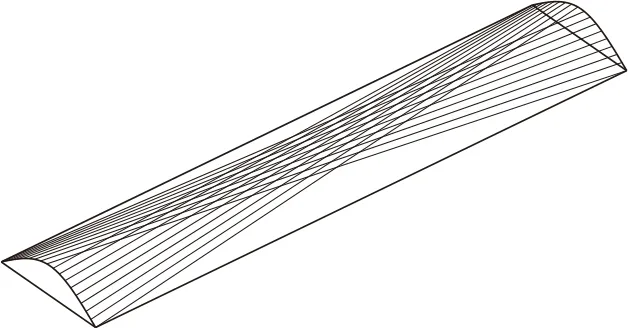
图1 双曲抛物面空间缆索分布形式Fig.Spatial cable distribution of hyperbolic paraboloid
如图2 所示, 设置多道钢结构曲梁放置在双曲抛物面索网之上, 采用夹具将平行钢丝缆索和双曲抛物面索网与钢结构曲梁牢固连接, 加强空间缆索体系的空间刚度和整体性, 也可方便斜向吊杆的安装, 可确保加劲梁桥面系与空间缆索体系共同受力工作。

图2 双曲抛物面混合空间缆索人行景观桥构形Fig.2 Configuration of hyperbolic paraboloid hybrid spatial cable pedestrian landscape bridge
新型空间混合缆索和传统的抗风缆索的上下二套柔性缆索协同工作, 双曲抛物面空间缆索在上面吊住悬索桥桥面系, 传统的抗风缆索在下面拽住悬索桥桥面系, 可以牢牢固定悬索桥桥面系, 从而可以大幅度提高人行悬索桥的抗扭频率。本工程的超大跨径人行悬索桥效果如图3 所示。

图3 双曲抛物面混合空间缆索人行景观桥效果Fig.3 Effect of hyperbolic paraboloid mixed space cable pedestrian landscape bridge
2 有限元建模
某峡谷景区人行大跨径悬索桥, 主跨径为480m, 桥面全宽8m, 采用卵蛋拱形桥塔的空间缆索人行悬索桥方案。
卵蛋拱形桥塔由抛物线段塔顶和左右两个椭圆弧线段塔柱组成, 桥塔最高处为68m, 桥塔最宽处为50m, 其中抛物线段塔顶的宽度为40m,矢高为8m, 椭圆弧线段塔柱高度为60m, 卵蛋拱形桥塔采用直径为5m 的圆形钢管, 钢管壁厚为20mm, 内灌注C60 混凝土, 卵蛋拱形桥塔采用桩基础, 倾斜角度为15°。
空间缆索体系由平行钢丝缆索和双曲抛物面碳纤维索网组成, 平行钢丝缆索采用1670MPa 的高强钢丝缆索, 左右两股平行钢丝缆索间距为8m, 每股直径均为0.4m, 竖向钢丝吊杆间距为8m, 共计2 ×59 根吊杆。
为了平衡悬索桥拉力, 每侧设置四根斜拉背索, 一端锚固在卵蛋拱桥塔中, 另一端锚固在隧道式锚碇中, 四根斜拉背索分为左右两组, 斜拉背索采用1670MPa 高强钢丝, 每根高强钢丝直径为0.6m。
双曲抛物面索网采用3500MPa 的高强碳纤维缆索, 全桥共10 根, 每根主缆直径为0.05m。带有下拉杆的钢结构曲梁设置在双曲抛物面索网和两股平行钢丝缆索之上, 钢结构曲梁间距24m, 共计19 根, 曲梁两端设置斜向碳纤维吊杆与加劲梁相连, 斜向碳纤维吊杆间距24m, 共计2 ×19 根斜向吊杆。抗风主缆索为左右两股直径为0.2m 的高强钢丝缆索, 连接拉杆间距为8m,共计2 ×59 根连接拉杆。
桥面加劲梁采用钢梁格结构, 高度为600mm, 钢梁宽度为300mm, 150mm 透明钢化玻璃内嵌于钢梁格结构之中, 桥面加劲梁在跨中处设置一个观光圆环, 圆环内直径14m, 圆环外直径20m。
本工程采用Midas 软件建模并计算。采用索单元模拟缆索部分, 卵蛋拱桥塔、桥面系加劲梁及钢结构曲梁等构件采用三维空间梁单元建模。
按照零位移原则, 按抛物线形建模并施加相应的自重荷载, 给索单元设置初始应变, 计算出悬索的位移, 然后不断更新节点坐标和索单元初拉力来求平衡状态, 得到主缆的初始应力状态后, 通过反复修正来使成桥状态的有关控制参数满足要求, 从而得到主缆的成桥线形。MIDAS 模型如图4 所示。
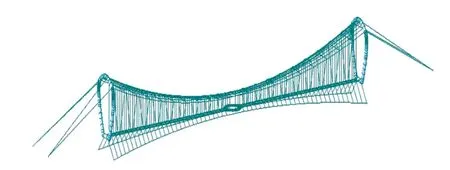
图4 Midas 有限元模型Fig.4 Midas finite element model
3 竖向荷载作用下的计算结果
对主跨桥面做满荷加载, 桥面附加恒荷载采用均布荷载标准值10kN/m2, 桥面活荷载采用均布荷载标准值5kN/m2。对直接受荷载的加劲梁作内力分析, 计算结果见图5 ~图7。

图5 竖向荷载作用下位移计算结果(恒+活)(单位: m)Fig.5 Displacement calculation results under vertical load(Dead load +live load)(unit: m)

图6 内力计算结果(恒+活)(单位: kN)Fig.6 Internal force calculation results(Dead load +live load)(unit: kN)
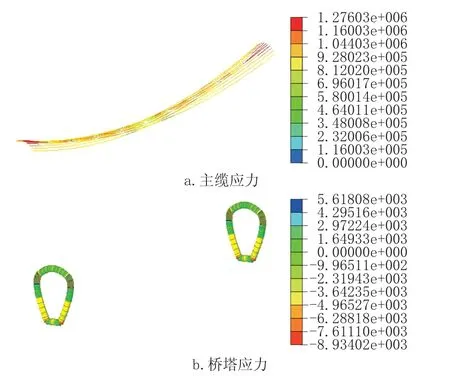
图7 应力计算结果(恒+活)(单位: kN/m2)Fig.7 Stress calculation results(Dead load +live load)(unit: kN/m2)
由以上计算结果可知, 在竖向恒活荷载作用下, 最大竖向位移出现在跨中位置, 最大位移为0.373m, 满足规范规定1/800 限值要求。
碳纤维主缆最大内力为62637.0kN, 碳纤维主缆最大应力为1276.0MPa, 满足强度要求。钢主缆最大内力为155567.7kN, 钢主缆最大应力为792.3MPa, 满足强度要求。桥塔最大内力为334467kN, 桥塔最大应力为89.3MPa, 桥塔材料采用钢管混凝土, 混凝土采用C60 混凝土, 钢材选用Q355 钢材, 可以满足强度要求。
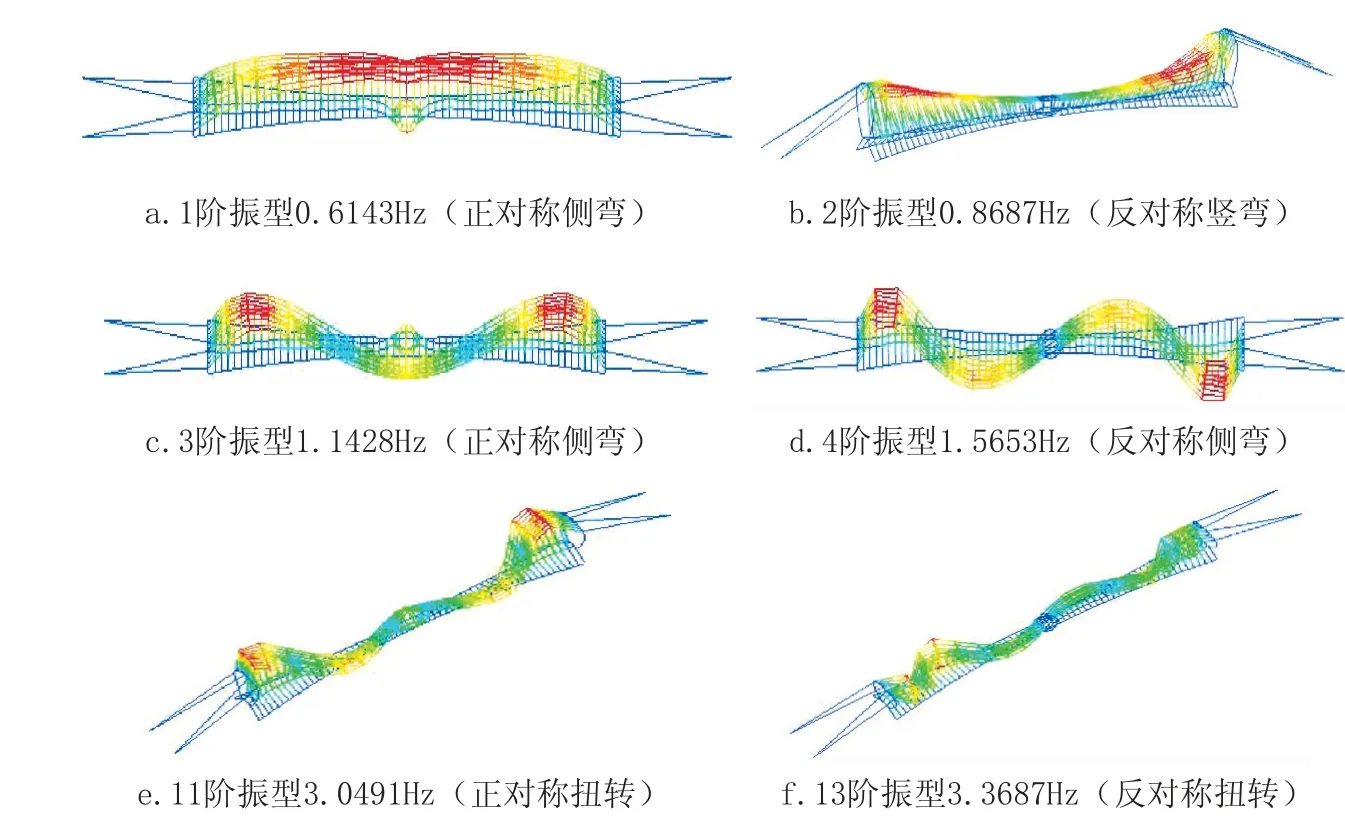
图8 典型振型Fig.8 Typical vibration mode
4 动力模态分析
主缆是悬索桥的主要承力结构, 动力特性分析必须考虑重力刚度的影响, 建模时以初拉力的形式计入主缆、吊索的成桥内力。基于Midas 的非线性静力分析、应力刚化效应和模态分析功能, 进行自振特性分析。为了不遗漏任何振型,分析过程中采用子分块法求解特征方程、自振频率以及振型特点, 双曲抛物面混合缆索空间悬索桥比较有代表性的振型见图8。
由图8 中的计算结果可知,第1 阶振型为正对称侧弯, 频率为0.6143Hz; 第2 阶振型为反 对 称 竖 弯, 频 率 为0.8687Hz; 第11 阶振型为正对称扭转, 频率为3.0491Hz; 第13 阶振型为反对称扭转, 频率为3.3687Hz。整体来看, 振型密集, 出现明显的振型分组现象, 前10 阶振型主要以侧弯、竖弯振动为主, 直到第11 阶才出现正对称扭转振型。先发生正对称扭转振动, 后发生反对称扭转振动, 扭弯频率比值为3.51 较高, 表明本工程悬索桥结构具有良好的空间刚度。
5 抗风稳定性研究
在实际工程中, 悬索桥的横断面大都是非流线型的, 故对分离流扭转的颤振临界风速应用较为广泛。本章采用分离流扭转的颤振临界风速计算中的Selberg 公式来分析悬索桥的颤振稳定性:
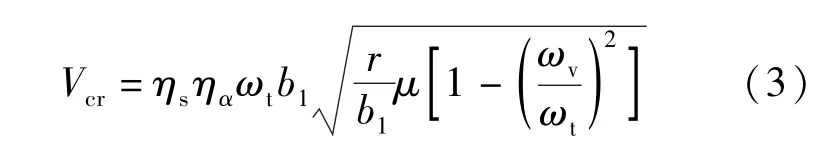
式中:ηs是主梁截面形状影响系数,ηα是攻角效应系数, 对于0 度风攻角下的平板断面,ηs、ηα均取1.0;r是桥梁断面(包括加劲梁和主缆)惯性半径;b1为加劲梁截面的半桥宽;μ为桥梁与空气的密度比;m为加劲梁及主缆的质量密度;ρ为空气密度;ωt、ωv分别为最低阶扭转圆频率和竖向圆频率。本设计中,ηs、ηα均取1.0。经过计算,r=9.15m,μ=2.12,ωt、ωv分别为13.94rad/s、3.97rad/s。因此, 本设计悬索桥的颤振临界风速为:
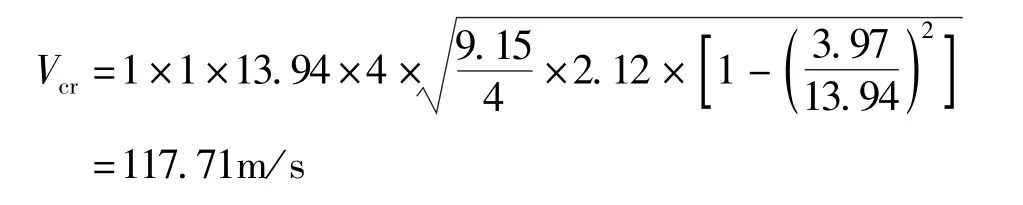
由此, 该桥的颤振临界风速较高, 满足本工程72m/s 的设计风速要求, 具有良好的抗风稳定性。
6 对比分析
为了验证双曲抛物面混合空间悬索桥的优势, 建立平行悬索桥的有限元模型, 开展对比分析, 平行悬索桥的Midas 模型如图9 所示。

图9 平行悬索桥Midas 有限元模型Fig.9 Midas finite element model of parallel suspension bridge
平行悬索桥的典型振型及振型频率计算结果如图10 所示。由图10 中的计算结果可知, 平行缆索悬索桥第1 阶振型为正对称侧弯, 频率为0.4721Hz; 第4阶振型为正对称竖弯, 频率为0.6408Hz; 第6 阶振型为正对称扭转, 频率为0.7703Hz; 第8阶振型为反对称扭转, 频率为0.9052Hz。扭 弯 频 率 比 值 为1.20, 抗风稳定性较差。
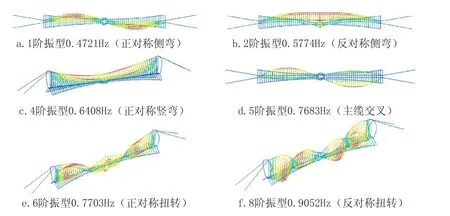
图10 平行悬索桥典型振型Fig.10 Typical vibration mode diagram of parallel suspension bridge
由公式(3)可以计算得到平行悬索桥的颤振临界风速。平行缆索悬索桥的相关参数取值如下:r= 4.95m,μ= 2.12,ωt、ωv分 别 为4.840rad/s、2.966rad/s。因此, 平行缆索悬索桥的颤振临界风速为:
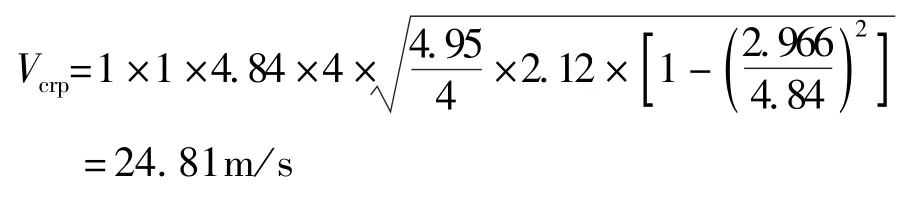

表1 平行悬索桥与双曲抛物面悬索桥对比Tab.1 Comparison between parallel suspension bridge and hyperbolic paraboloid suspension bridge
如表1 所示, 相对于平行缆索悬索桥, 双曲抛物面混合缆索空间悬索桥扭转频率提高295.8%, 扭弯比提高192.5%, 表明空间缆索体系大大提高了悬索桥的空间刚度; 颤振临界风速较平行缆索悬索桥提高374.4%, 表明双曲抛物面混合缆索空间悬索桥具有良好的抗风稳定性。
为满足行人的舒适性要求, 我国现行规范规定, 人行桥的竖弯基频应不小于3Hz。然而, 对于旅游景区大跨径悬索桥这种柔性结构, 很难满足这一要求, 本工程通过设置质量调节阻尼器,可改善大跨径悬索桥的行人舒适度。
为了证实双曲抛物面形空间缆索悬索桥的合理性, 选取两座传统的人行悬索桥进行对比分析, 将本设计的双曲抛物面人行悬索桥的模态振型主要指标与所选取两个人行悬索桥进行对比,对比结果见表2。
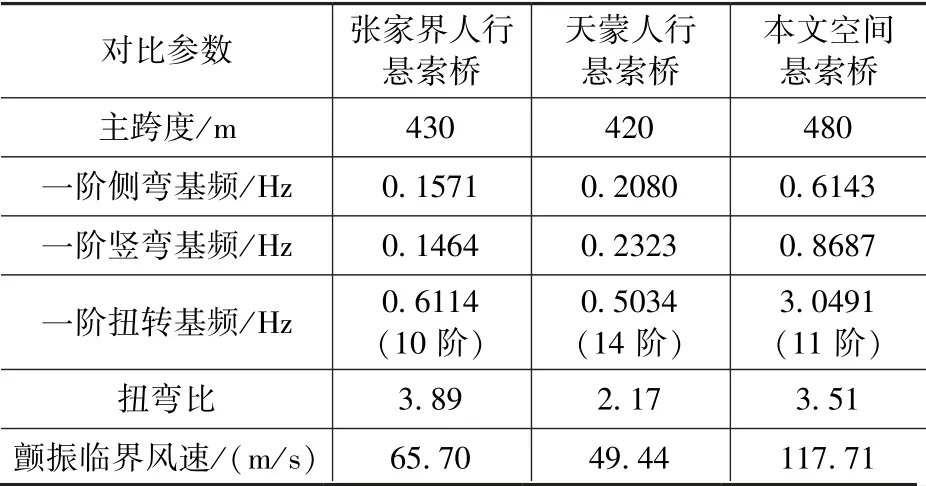
表2 双曲抛物面悬索桥与其他人行悬索桥对比Tab.2 Comparison between hyperbolic paraboloid suspension bridge and other pedestrian suspension bridges
通过对比可见, 相比于两座对照的人行悬索桥, 本设计的双曲抛物面悬索桥人行悬索桥的一阶侧弯、一阶竖弯、一阶扭转基频和扭弯比明显更高, 其颤振临界风速远远大于对比桥梁, 证实双曲抛物面形空间缆索悬索桥具有良好的抗风稳定性。
7 结论
本文以某峡谷景区的500m 级双曲抛物面空间混合缆索体系悬索桥为背景, 建立Midas 有限元模型, 进行静力分析、模态分析和抗风稳定性分析, 得出以下结论:
1.双曲抛物面空间混合缆索体系悬索桥, 平行缆索承担竖向荷载, 碳纤维双曲抛物面空间缆索和抗风缆索两套缆索可大幅度提高抗扭刚度。
2.碳纤维双曲抛物面空间缆索和抗风缆索两套缆索协同工作, 优势互补, 上下左右四组抗风拉索紧紧拽住桥面系, 可大幅度提高抗风稳定性。
3.前10 阶振型主要以侧弯、竖弯振动为主,直到第11 阶才出现正对称扭转振型(3.0491Hz)。先发生正对称扭转振动, 后发生第13 阶反对称扭转振动(3.3687Hz), 扭转频率较高, 双曲抛物面空间交叉缆索、抛物线刚性曲梁和抗风缆索形成了强大的空间缆索体系, 具有良好的空间刚度。
4.双曲抛物面形空间缆索体系抗扭刚度较大, 能显著提升悬索桥的颤振稳定性, 本设计的500m 级人行景观窄幅悬索桥一阶正对称扭转基频高达3.0491, 扭弯频率比值为3.51, 颤振临界风速为117.71m/s 较高, 满足本工程72m/s 的设计风速要求。

