顶管管顶竖向土压力计算探讨

范毅雄

(中国市政工程中南设计研究总院有限公司 武汉430010)

引言

各国顶管设计规范中, 顶管管顶竖向土压力的计算公式在形式上有所不同, 日本下水道管渠推进技术协会规范[1]采用太沙基松弛土压力公式计算,德国水资源管理协会规范[2]和污水处理技术协会规范[3]根据筒仓理论计算, 美国土木工程师协会规范[4]采用马斯顿-斯潘格勒公式计算, 但差别只是形式上的, 德、美规范中计算公式实际上和太沙基松弛土压力公式是一致的, 都遵循相同的理论假设和推导过程, 只是计算参数的取值有区别。

决定松弛土压力的主要是剪切面形态及其间距、剪切阻力计算参数、地面荷载等几个关键计算参数, 日、德、美规范对这些参数的取值是不同的, 中国规范则主要参考美国规范的做法。本文期望通过对各国规范不同参数取值方法的分析和比较, 综合总结, 得到一个更全面、合理、便捷的计算公式。

1 太沙基松弛土压力公式

太沙基(1943)[5]对活门试验[6]进行总结,基于以下三条假设推导了平面应变状态下的松弛土压力公式: ①剪切面竖直平行, ②任意水平面上松弛土压力均匀分布, ③剪切面上的剪切阻力按摩尔-库仑公式计算。计算模型如图1 所示。

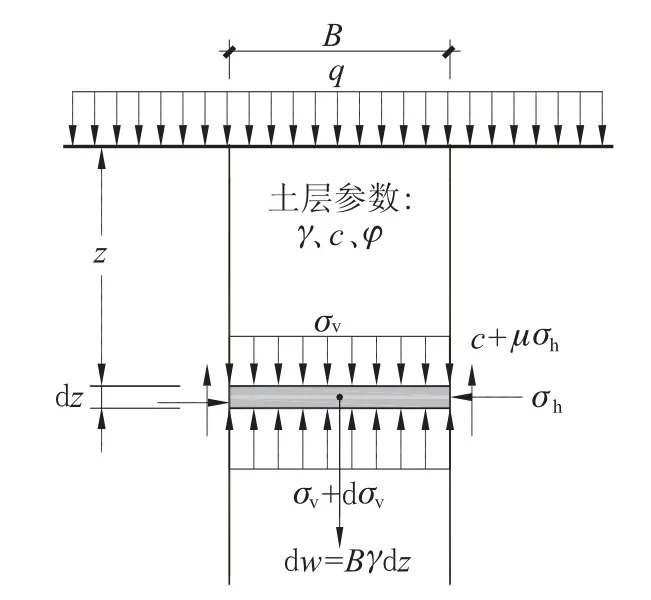
图1 太沙基松弛土压力计算模型Fig.1 Terzaghi relaxation earth pressure calculation model

其中B为剪切面间距(本文和德、美规范一致定义为B, 太沙基原文和日本规范则定义为2B以简化公式),q为地面分布荷载,γ为土体重度,c为土体内聚力,φ为土体内摩擦角; 取深度z处的微单元dz,σv为竖直松弛土压力,σh为水平土压力, 引入水平土压系数K, 令σh=Kσv; 则根据摩尔-库仑公式, 剪切面上的剪切阻力为c+μσh=c+Ktanφσv。

对单位宽度的微单元dz列力的平衡方程得到一个一次线性常微分方程, 再结合边界条件:z=0处σv=q, 可解得深度z处松弛土压力公式(1):

顶管掘进使其上方的土体向下沉降, 符合太沙基松弛土压模型, 顶管管顶竖向土压力可按公式(1)计算。由图1 可知, 将公式(1)应用于顶管需解决以下两个问题: ①剪切面形态及其间距和顶管管道的关系; ②剪切面上剪切阻力的计算参数(K、c、φ)如何取值。对此日、德、美规范采取了不同方法。

2 各国顶管设计规范

2.1 日本下水道管渠推进技术协会规范

1.剪切面形态及其间距

日本规范完全按照太沙基理论[5], 规定管道两侧的剪切面倾角按主动土压力破坏面倾角45° +φ/2 取值, 管顶以上剪切面为竖直, 计算模型如图2 所示。

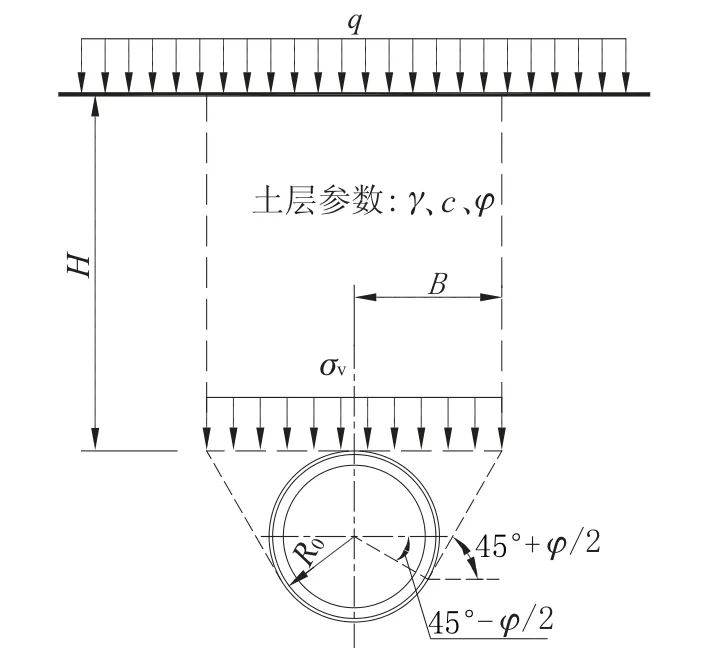
图2 日本下水道管渠推进技术协会规范计算模型Fig.2 Calculation model of Specification for Japan sewer jacking Technology Association

日本规范取剪切面间距为2B, 则B=R0cot其中R0为顶管掘削毛洞的半径,并规定R0比管道外半径大50mm。

除了B的取值, 日本规范中松弛土压力计算公式和公式(1)一致, 故不再罗列。

2.剪切阻力计算参数

太沙基(1936)[6]认为K值从约为1 的数值增大到约为1.5 的极大值, 由于K越小则剪切阻力越小, 松弛土压力越大, 因此日本规范取K=1。

日本规范对于c、φ的取值方法也基本和太沙基理论[5]一致, 但对于是否在计算中考虑c的作用, 日本规范认为: 计算松弛土压时如果考虑c, 某些情况下计算结果会太小甚至为负值, 与实际不符且不安全。因此规定: 对于标贯值N＜2的软粘土不考虑c; 对于标贯值N≥25 的粘性土,c采用地勘报告所给标准值的一半。

3.分层土计算

日本规范中推导了分层土条件下的松弛土压力, 这部分内容是德、美规范所没有。其方法是将上一土层底部的松弛土压力视为下一土层顶部的均布荷载, 然后迭代应用公式(1), 就可算得多层土条件下管顶的松弛土压力。限于篇幅, 本文不罗列具体公式。

同时, 日本规范规定对于埋深小于10m 的顶管, 可按厚度加权平均各土层参数(γ、c、φ),从而将分层土转化为均质土来计算; 而对于埋深大于10m 的顶管则要求按分层土计算。

2.2 德国水资源管理协会规范和污水处理技术协会规范

1.剪切面形态及其间距

德国规范的计算模型和日本规范基本一致,但认为管道两侧的剪切面与水平面夹角一般大于60°, 因此规定夹角恒取60°, 计算模型如图3,则其中Da为管道外径。

2.剪切阻力计算参数

德国规范规定计算时不考虑c的作用, 并在计算公式中采用剪切面上的计算内摩擦角δ替换φ。对于参数K和δ, 德国规范[2]在第4.4 节的表3 和表4 中给出了对于不同土质的建议值, 见本文表1、表2。其中φ′为有效内摩擦角。

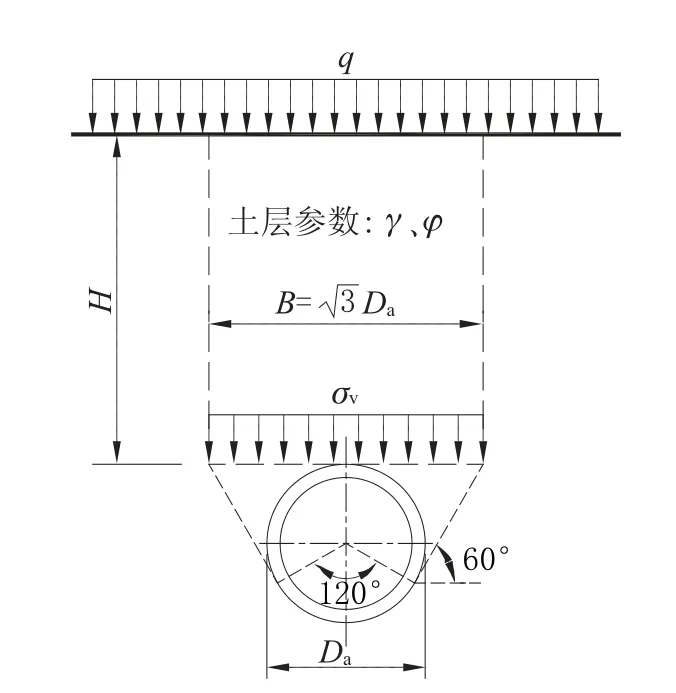
图3 德国水资源管理协会规范计算模型Fig.3 Calculation model of specification for german water resources management association

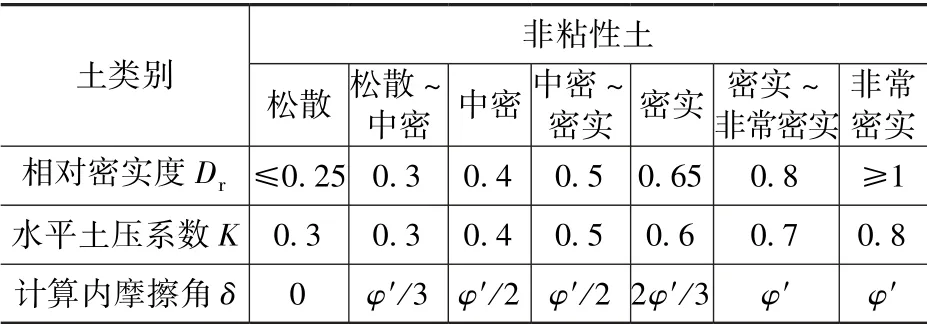
表1 非粘性土水平土压系数和计算内摩擦角Tab.1 Horizontal soil pressure coefficient and calculated internal friction angle of non-cohesive soil

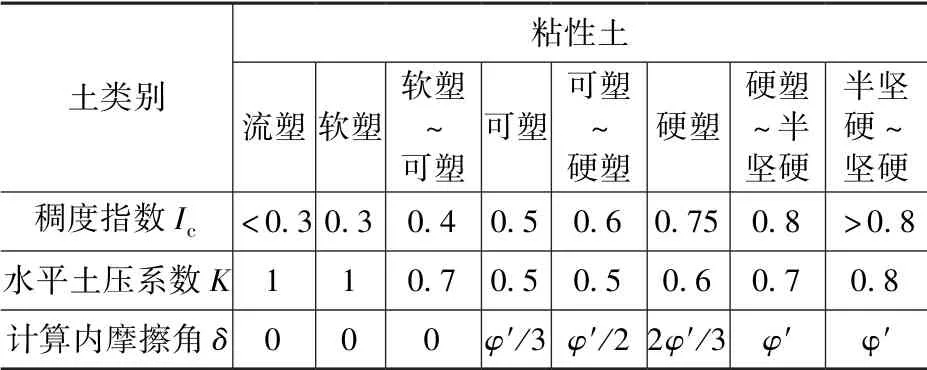
表2 粘性土水平土压系数和计算内摩擦角Tab.2 Horizontal soil pressure coefficient and calculated internal friction angle of clayey soil

德国规范规定在无地勘报告时, 非粘性土φ′取30° ～35°, 粘性土φ′取20° ～25°。

3.德国规范公式

和日本规范不同, 德国规范引入松弛土压力系数κ和κ0, 将公式表达为管顶全土柱压力的折减形式如公式(2) ～公式(4):

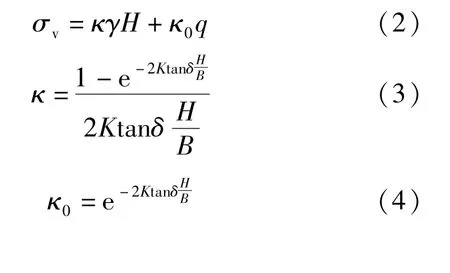
对于κ和κ0, 除了表1、表2 中注1 的规定,附加规定以下情况时取κ=1: ①当采取施工措施使得顶管掘进过程中没有发生地面沉降, ②管顶覆土厚度小于管道直径, ③水下顶管, ④膨胀土中顶管; 并规定当q为随时间变化的荷载时κ0=1。即这些情况下应按管顶全土柱压力计算而不能折减。

2.3 美国土木工程师协会规范

1.剪切面形态及其间距

美国规范采用的马斯顿-斯潘格勒公式源于开槽埋管, 推广至暗挖管道后沿用了自管道两侧竖直向上的剪切面, 因此剪切面形态和日、德规范不同, 其剪切面间距B取掘削孔径Bth, 计算模型如图4 所示。

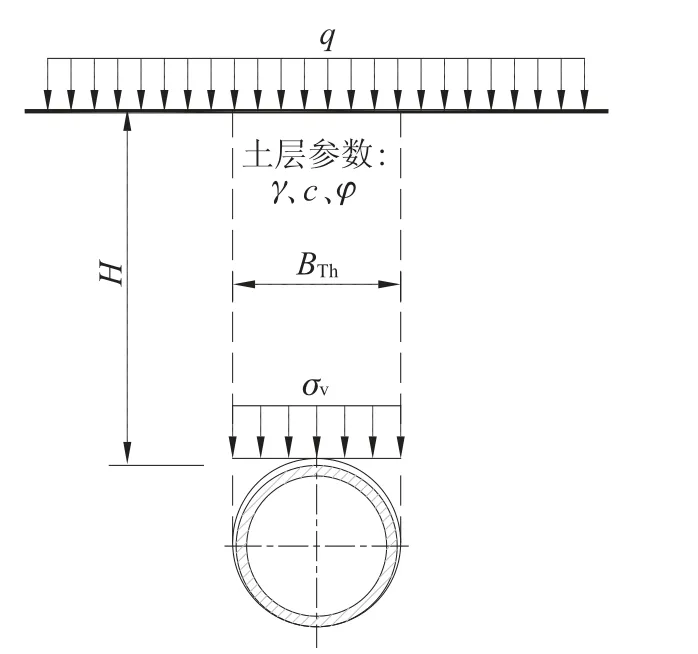
图4 美国土木工程师协会规范计算模型Fig.4 Calculation model of specification for the american society of civil engineers

2.剪切阻力计算参数

美国规范规定c的设计值取实验值的33%,如果没有实验值, 则按表3 取值。

表3 内聚力设计值Tab.3 Design value of cohesion

美国规范认为c的取值应偏保守, 规定在以下条件下取c=0: ①在没有足够把握的情况下;②当土层因冰冻或干燥原因会季节性开裂时;③施工超挖较多且施工完成之后没有回填密实。

对于K和φ, 美国规范的做法则是将公式(1)中的Ktanφ合并为参数K′μ, 并对于不同土质给出建议值, 见表4。美国ASCE 手册[7]中对这些参数如何取值作了详细阐述。

表4 K′μ和重度设计值Tab.4 design value ofK′μ and density

3.美国规范公式

和德国规范类似, 美国规范的公式也采用了全土柱压力的折减形式; 不同的是对于地面荷载q, 美国规范规定将其转化为等效厚度的覆土,因此公式中不含q项。

由于美国规范依据的马斯顿公式是根据力的平衡推导的, 最后得到的是管顶总的力而不是应力, 本文将其除以管道外径转换为应力形式的公式, 并在符号上和公式(2) ～公式(4)保持统一,得到:

2.4 中国国家规范和中国工程建设协会规范

1.剪切面形态及其间距

中国国家规范[8]采用了和日本规范相似的做法, 但剪切面起点不同, 计算模型如图5 所示,则按本文符号表达的剪切面间距为:B=Da中国工程建设协会规范[9]沿用了国家规范的公式。

2.剪切阻力计算参数

中国国家规范不考虑内聚力c的作用; 并参考美国规范将Kμ合并取值, 统一取了表4 中碎石对应的0.192; 公式表达和美国规范相同之处是采用了管顶总的力的形式, 即得到的沿管道纵向的线分布力, 不同之处则是将土压力系数公式(5)分母中的H/B代入到土压计算公式(6)中消去了H。

中国工程建设协会规范则考虑了内聚力c的作用, 并规定取地质报告中的最小值; 对于Kμ合并的取值, 则参考美国规范, 按表4 分别规定了饱和粘土、普通粘土、砂砾的取值; 公式表达采取了和国家规范相同的化简处理。

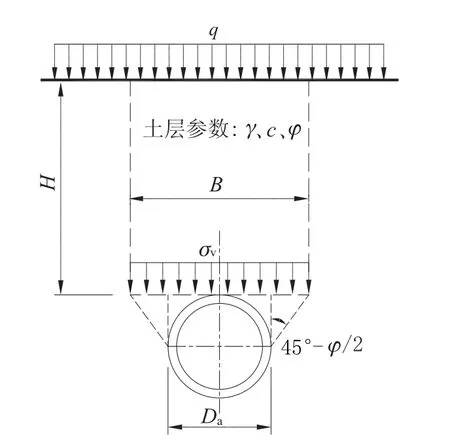
图5 中国规范计算模型Fig.5 Calculation model of chinese specification

另外, 中国国家规范和中国工程建设协会规范都没有考虑地面荷载q的作用。

3 综合分析

3.1 剪切面形态及其间距

美国规范沿用了马斯顿-斯潘格勒公式中自管道两侧竖直向上的剪切面, 但首先顶管掘进施工时不可避免地对周围土体产生扰动, 使得剪切面间距加大, 其次在相同条件下B越大则σv越大, 日、德规范中B的取值比美国规范更安全,因此不推荐采用美国规范的做法。

日本规范采用原始的太沙基理论, 对不同内摩擦角的土层分别计算B, 但管道两侧剪切面的倾角实际上和土体的c和φ都有关, 因此对于某些c较大而φ较小的粘土, 会使计算所得的B过大而不符合实际情况。

中国规范和日本规范类似, 但两者的剪切面起点不同, 且日本规范中采用挖掘毛洞直径代替管道直径, 相同条件下日本规范的计算结果会稍大一些。

德国规范则基于工程经验认为剪切面倾角最小为60°, 因而规定B等于倍管道外径, 这种方法比较简便易用, 也能保证安全, 因此本文推荐采用德国规范的模式, 或者即使采用日本规范的模式, 也要采用考虑内聚力的综合内摩擦角来计算B。

3.2 剪切阻力计算参数

1.关于内聚力c

日、美规范都规定可以考虑c的作用, 但同时为了避免当2c接近甚至超过γB时, 计算所得松弛土压力太小甚至为负值, 两者都规定在某些条件下不考虑c的作用, 而且在考虑c的作用时,日本规范还规定c值取地勘报告结果的1/2, 美国规范则是取1/3。

中国国家规范不考虑c的作用。中国工程建设协会规范考虑了c的作用, 但规定c值宜取地质报告中的最小值。在c的折减这一点上中、美规范的做法哪个更安全取决于实验值的离散性,如果离散性大则中国规范更安全, 反之则美国规范更安全, 但由于实验值的允许最大偏差是受限制的, 因此实际上美国规范更安全。

而德国规范则明确规定不考虑c的作用, 并基于此采用剪切面上的计算内摩擦角δ替换φ。

由于考虑c的作用时, 当2c大于γB时松弛土压力计算值为负值, 特别是对于管径较小的微型顶管尤其如此, 而为此作很多补充规定来避免这种情况, 对于设计而言不太便捷, 因此本文推荐的计算公式采用德国规范的方法。

2.关于K和μ

日本规范采用原始的太沙基理论[5], 取K=1,μ=tanφ。但Handy (2004)[10]的研究指出随着剪切面上的剪切位移增加, 水平土压系数K由静止土压系数变化为主动土压系数, 因此太沙基公式[5]中取K=1 应予以修正。

德、美规范则对不同的土质列表给出了推荐参数值, 德国规范是分别列出K和δ值, 美国规范则是将Ktanφ合并成一个参数K′μ。

Moser[11]认为K应按朗肯土压力系数取值,并给出了K、μ的经验值如表5 所示, 由此计算得到的K′μ和美国规范中的取值基本一致。

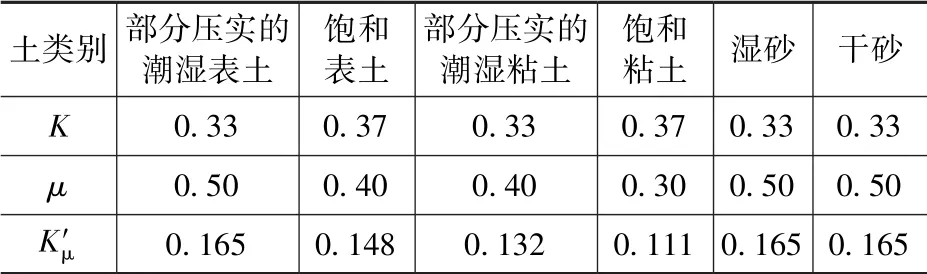
表5 K、μ 的经验值Fig.5 Experience value ofK、μ

而德国规范认为顶管掘进施工一般会采取措施减小地面沉降, 剪切面上实际发生的剪切位移达不到综合内摩擦角φ′所对应的剪切位移值, 根据土力学原理, 如图6 所示, 例如当实际发生的剪切变形仅为φ′对应值的1/10 时, 此时剪切面上起作用的δ≈φ/2。

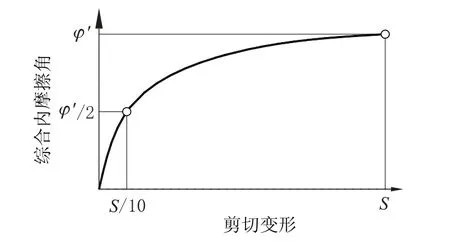
图6 内摩擦角和剪切变形的关系Fig.6 Relationship between internal friction angle and shear deformation

表6、表7 根据表1、表2 计算Ktanδ值, 和美国规范的K′μ进行对比。

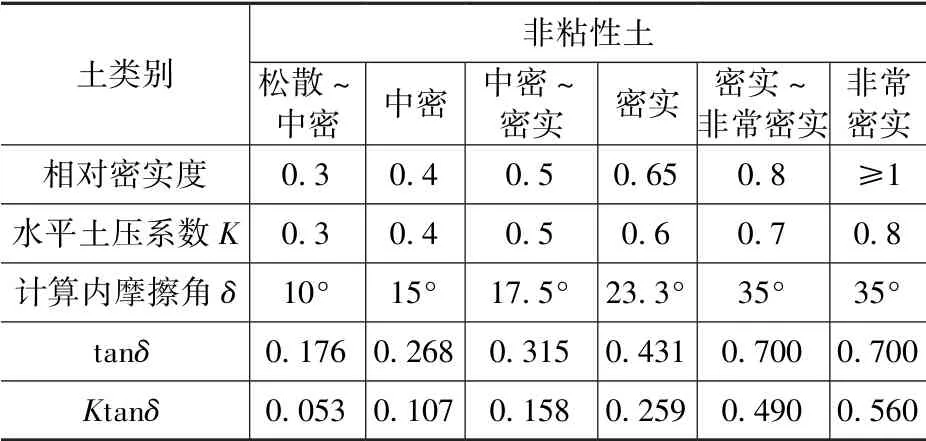
表6 非粘性土Ktanδ 值Tab.6 K ofδ non-cohesive soil

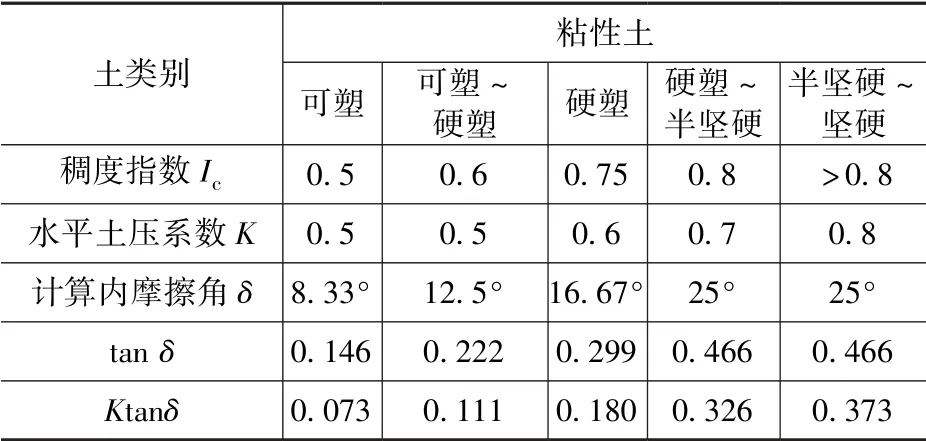
表7 粘性土Ktanδ 值Tab.7 Ktanδ of cohesive soil

和表4 对比可见, 对于松散～中密的非粘性土和可塑的粘性土, 德国规范的参数取值低于美国规范; 对于密实以上的非粘性土和硬塑以上的粘性土则相反。由于Ktanδ和K′μ代表剪切面上的摩阻系数, 其值越小则竖向松弛土压力就越大,对于一般的松散～中密的非粘性土和可塑的粘性土德国规范更偏于安全, 而对于密实和坚硬的土相反。

相对于美国规范, 德国规范的表格根据相对密实度和稠度系数对土进行了详细分类, 实际应用时更合理, 可操作性也更强, 推荐采用。

3.3 关于地面荷载q

日、德规范公式都包含了地面荷载q项, 而美国规范则建议将q折算成等效覆土厚度, 但这种处理方式存在问题。假设将q折算成等效覆土层, 其厚度H等效=q/γ, 按公式(1)计算, 在减去等效覆土层两侧剪切面的摩阻力之后, 传递到等效覆土层底面处的土压是小于原始的q=γH等效的。而中国国家规范和中国工程建设协会规范也都不包含q项, 且并未给出如美国规范那样的处理方式, 则地面荷载q如存在, 将按应力扩散的方式传至管顶, 这也存在问题。

按图1 模型,q应在顶管施工过程中存在,即从剪切面产生到应力完成转移的过程中存在,在此期间q无论是满布还是仅局部施加于宽度B的范围内, 对松弛土压力的影响都是一致的; 而在顶管施工结束后, 即应力完成转移后, 再施加的荷载则不能按图1 模型计算, 而要按应力扩散的方式计算。所以本文第2.2 节第3 条德国规范的附加规定中关于κ0=1 的规定即针对这种情况。由此可见, 公式中的q项是针对顶管施工期间的荷载, 和顶管施工完成后使用期间再施加的荷载应加以区别。

另外从应用的角度, 公式中包含q项, 可以方便推导分层土的松弛土压力。

3.4 推荐计算公式

为方便应用, 推荐计算公式采用德国规范的全土柱压力折减形式, 并且采用类似美国规范的K′μ参数形式。因此在公式(2) ～公式(4)的基础上, 将代入, 并定义土压折减系数K1、荷载折减系数K0、剪切阻力系数Kμ, 令Kμ=得到推荐公式(7) ～公式(9):

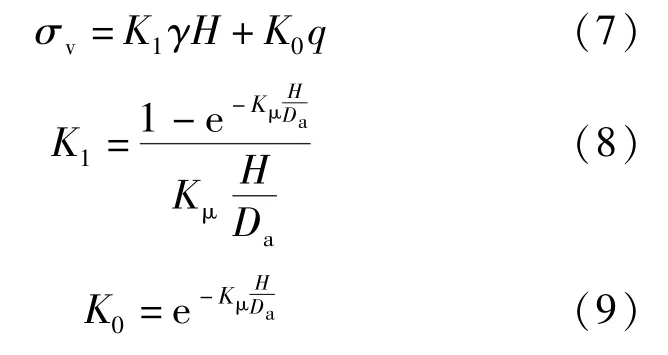
式中:K1、K0、Kμ可按表8、表9 取值, 并遵守本文第2.2 节第3 条的附加规定。

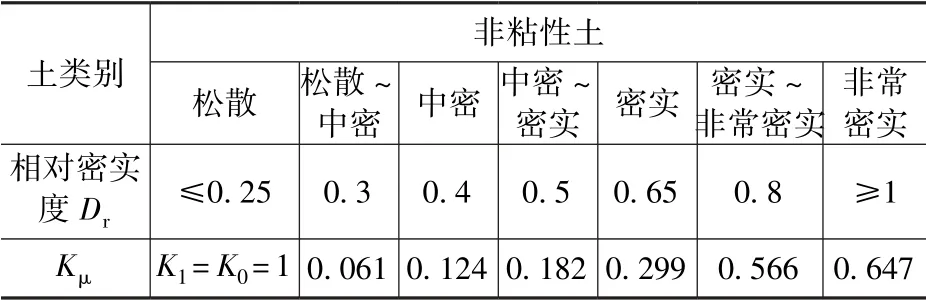
表8 非粘性土K1、K0、KμTab.8 K1、K0、Kμ of non-cohesive soil

表9 粘性土κ、κ0、KμTab.9 κ、κ0、Kμ of cohesive soil

之所以推荐采用德国规范的全土柱折减形式, 不仅是因为这样的表达形式物理意义比较明确, 更重要的是因为折减系数K1、K0仅由变量H/Da, 即覆土厚度和管径的比值确定, 可以绘制后面的图7, 方便工程应用。

3.5 关于公式计算结果的连续性

活门试验[6]显示土层厚度大于1 倍活门宽度是土拱效应形成的必要条件, 据此德国规范和中国规范都规定: 当管顶覆土厚度小于管道直径时按全土柱压力计算。即本文第2.2 节第3 条的附加规定②, 但此规定会造成公式计算结果的不连续。

不考虑q的影响, 则依以上规定, 当H/Da≤1.0 时, 取σv=γH; 而当H/Da=1.0 时, 按公式(7)计算, 松弛土压力σv=K1γH, 由于K1＜1.0,就意味着当H/Da由小于1.0 的区间增大至进入大于1.0 的区间时, 在H/Da=1.0 这个节点上σv发生了突变, 并且是变小了。所以此附加规定应修正为: 当H/Da≥1.0 时, 如K1γH＜γDa, 取K1γH=γDa。如此可使公式计算结果保持连续。

3.6 公式应用图表

不考虑q的影响, 将松弛土压力σv转换为一个折减高度(设为H′)的土柱压力, 则H′=K1H, 因此H′/Da=K1H/Da, 由此可以绘制折减土柱高度相对管径比值如图7 所示。

图7 折减土柱高度相对管径比值Fig.7 Ratio of soil column reduced height to pipe diameter

图7 显示随着Kμ的减小, 比值曲线依次有规律地向上排列, 因此实际应用时可根据Kμ值在图7 中取两条曲线进行插值。从图7 还可看到随着覆土厚度增大, 折减土柱高度相对管径比值趋向于一个极限值, 可由公式(7)、公式(8)推导该极限值为1/Kμ。

深度H处松弛土压力为:

当H/Da→∞时, 公式(10)的后面一项→0,此时H′→Da/Kμ, 即H′/Da→1/Kμ; 由于H→∞时,K0→0, 因此在考虑q的情况下, 极限值也相同。

3.7 分层土计算

根据第2.1 节第3 条的计算方法, 采用日本规范中的计算模型, 设第i层土的厚度为Hi, 剪切阻力系数为Kμi, 对地面荷载q按公式(7) ～公式(9)进行迭代计算可得到q传到管顶的压力公式(11)。

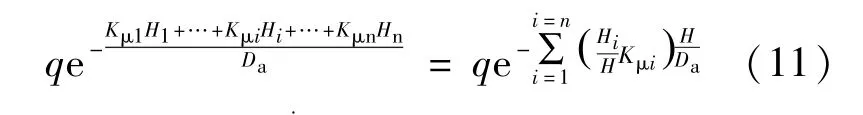
4 结语

通过对太沙基松弛土压力理论以及德、日、美、中等国规范中顶管管顶竖向土压力计算方法的分析和比较, 本文对剪切面形态及其间距、剪切阻力计算参数、地面荷载等几个关键计算参数的取值进行了探讨, 综合比较了各国规范对于这些关键参数取值方法后, 在德、美规范的基础上提出了一个推荐计算公式, 并绘制了相关的参数图表, 推导了分层土计算公式, 可供顶管设计参考。

存在的问题是: 本文主要基于理论推导和分析, 采用的计算参数主要基于德国规范, 一方面是和目前国内规范基于美国规范的计算参数有所区别, 需要协调, 另一方面是缺乏本国的工程实验数据的支持, 这都有待于进一步工作的补充和完善。