基于粒子群优化极限学习机及电容层析成像的两相流流型及其参数预测

张立峰, 朱炎峰

(华北电力大学 自动化系, 河北 保定 071003)

1 引 言

两相流在工业中广泛存在,流型是两相流的重要参数,实现流型实时监控对发展混流输送,提高安全等级,完善监督水平有着重要意义,因而,流型辨识在工业两相流研究中占据重要地位。电容层析成像(electrical capacitance tomography, ECT)技术是一种基于电容敏感机理的过程层析成像技术,由于其非侵入、可视化、结构简单、非辐射等优势受到学者广泛关注[1～3]。目前,常见的基于ECT技术的辨识方法主要分为3种:基于成像的流型辨识,该方法是通过ECT图像重建算法实现流型识别;基于数据特征的流型辨识,主要是应用统计学的方法观测不同流型的数据特性规律进行辨识;基于神经网络的流型辨识,该方法是将大量ECT采集到的数据与对应流型进行训练,建立合适的网络结构,从而对未知流型进行辨识[4,5]。相较而言,通过神经网络的方法进行流型辨识可以近似完成复杂的映射关系,预测结果也最为准确。极限学习机(extreme learning machine, ELM)是一种前馈神经网络,该算法具有优秀的泛化能力和学习速度[6,7],但由于其随机给定的输入权重和隐含层偏差导致该算法极不稳定,因此有学者尝试使用各种算法对ELM进行优化[8～11]。

目前已有的ECT流型辨识技术,通常只对流型进行分类辨识,但在实际工业生产过程中,亦需流型参数信息。本文针对这一问题,首先基于粒子群(particle swarm optimization, PSO)优化的极限学习机算法对流型进行辨识研究,再使用粒子群优化极限学习机(particle swarm optimization extreme learning machine, PSO-ELM)算法对流型参数进行预测,并与ELM算法预测结果进行了比较分析。

2 理论基础

2.1 电容层析成像技术原理

ECT系统主要分为3部分:电容传感器单元,数据采集单元和图像重建单元[3],如图1所示。不同介质对应的介电常数不同,所以当管道内的介质浓度和位置发生改变时,场内混流等价介电常数也随之发生变化,使其电容值也发生改变。ECT系统就是通过不同的电容值对管道内介质进行重建。本文使用的ECT系统的电容传感器为12电极传感器,每个流型对应66个独立测量电容值。

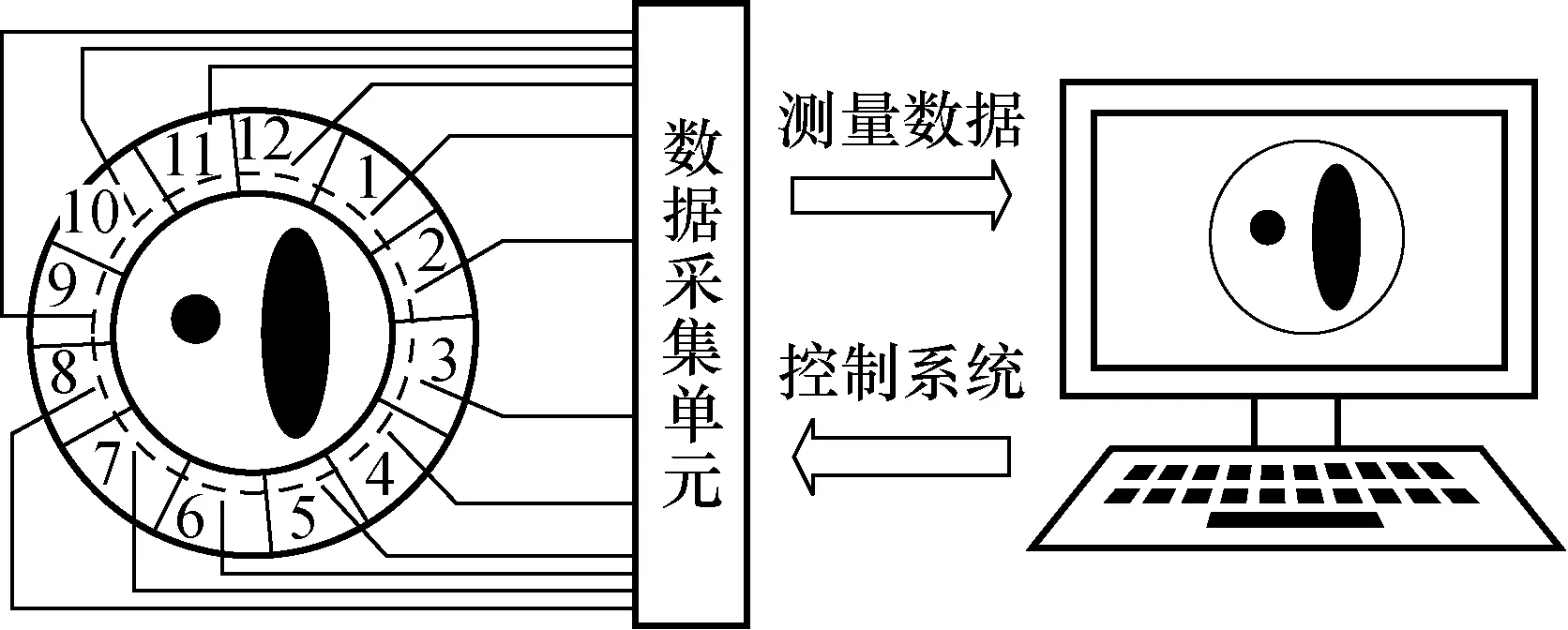
图1 ECT系统结构图Fig.1 Structure diagram of ECT system

2.2 极限学习机算法

对于N个任意不同的样本(xi,ti),其中,xi=[xi1,xi2,xi3,…,xin]T∈Rn,ti=[ti1,ti2,ti3,…,tim]T∈Rm,定义一个隐层节点数为,激活函数为g(x)的SLFNs的数学模型为[6～7]:

(1)

式中:j=1,…,N;wi=[wi1,wi2,…,win]T为连接输入层和第i个隐层节点的权重;βi=[βi1,βi2,…,βim]T为连接输出层和第i个隐层节点的权重;bi为第i个隐层节点的阈值;wi·xj为wi和xj的内积;oj为前馈神经网络的输出值;g(x)可选为Sigmoid函数或径向基函数等。

(2)

将式(2)简写为:

Hβ=T

(3)

式中:H为神经网络隐层的输出矩阵,H的第i列为受输入x1,…,xN输入所影响的第个隐层节点的输出。

根据ELM理论,在g(x)无限可微的条件下,wi和bi可随机选取。ELM开始学习后,wi和bi不作任何调整,即H保持不变。在一般情况下,隐层节点数量远小于训练样本数量,即≪N,导致矩阵H不是方阵,亦或有不存在βi使得Hβ=T成立的可能,将导致H不可逆。因而,将上述线性系统的极小范数最小二乘解改写为:

(4)

式中H†为矩阵H的Moore-Penrose广义逆矩阵。

2.3 粒子群优化算法

粒子群优化算法是一种受鸟类捕食活动启发而创造的优化算法。PSO算法首先在可行解中初始化一群粒子,每个粒子代表极值优化问题的潜在最优解,粒子特征由3个指标表示:位置,速度和适应度值。粒子在解空间中活动,并通过跟踪个体极值Pbest和种群极值Gbest来更新各个体位置。个体极值Pbest是在个体经历的位置中计算的适应度值的最佳位置。群体极值Gbest指的是搜索中所有粒子的适应度的最佳位置。每次更新粒子时,计算适应值一次,并通过比较新粒子的适应度值与个体极值和群体的适应度值来更新个体极值Pbest和群体极值Gbest位置[12～14]。

在D维空间中,由n个粒子构成的种群X=[X1,X2,…,Xn],其中第i个粒子的位置为Xi=[Xi1,Xi2,…,XiD]T。将Xi带入适应度函数f(Xi)中计算出适应度值粒子位置Fitness。第i个粒子的速度为Vi=[vi1,vi2,…,viD]T,其中粒子i的个体极值为Pi=[Pi1,Pi2,…,PiD]T,种群的全局极值为Pg=[Pg1,Pg2,…,PgD]T。

在每一次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置,更新公式:

(5)

式中:ω为惯性权重,调节最优解搜索范围;d=1,2,…,D,i=1,2,…,n,其中,n为种群大小;k为当前迭代次数;Vid为粒子速度;c1,c2(非负常数)为加速因子;r1,r2为2个随机数,取值范围为(0,1),以此来实现随机搜索;通常情况下,为了防止粒子盲目搜索,会将其位置和速度分别限制在[-Xmax,Xmax]和[-Vmax,Vmax]范围内。

2.4 粒子群优化极限学习机

由于ELM算法中的wi和bi随机选取,将会造成网络结构不稳定,存在输入权值和隐层阈值为0的情况,将导致部分隐层节点失效等问题。本文使用粒子群优化极限学习机算法,通过粒子群算法寻找合适的输入层权重和隐含层偏差,从而得到最优的ELM网络[15～16]。

PSO-ELM算法步骤如下:

1) 初始化粒子群算法的参数,主要包括:粒子群N,最大迭代次数tmax,c1=c2=2。

2) 设定隐含层神经元个数的值以及参数范围,从而构建ELM网络结构。

3) 根据w、β和b初始化粒子群,并确定粒子自身和群体的历史最优位置。

4) 将粒子群进行解码,得到w、β和b,计算训练样本的输出,k=1,2,…,n,n为训练样本的数量,并计算粒子群的适应度值。

5) 更新粒子飞行的权值、粒子群飞行的速度和位置。

6) 将每一个粒子的位置与粒子自身和群体的历史最优位置进行对比；如果更优,就更新相应的位置。

7) 更新当前迭代次数的数值,若当前迭代次数小于tmax时,则返回3)继续迭代。

8) 根据种群最优粒子位置得到ELM网络参数w、β和b,并建立的网络模型。

3 基于PSO-ELM的流型辨识

3.1 仿真条件及模型建立

本文选取油-气两相流为研究对象进行仿真实验,油相和气相的相对介电常数分别设置为3和1;采用12电极ECT传感器,其独立电容测量值的数量为66。以管道内半径为基准,进行无量纲化建模仿真。通过课题组编制的基于MATLAB的ECT仿真软件包进行传感器网格剖分、ECT正问题计算以及电容值的仿真计算。管内成像区域剖分网格如图2所示,管内剖分为12层,共计1 728个像素单元。

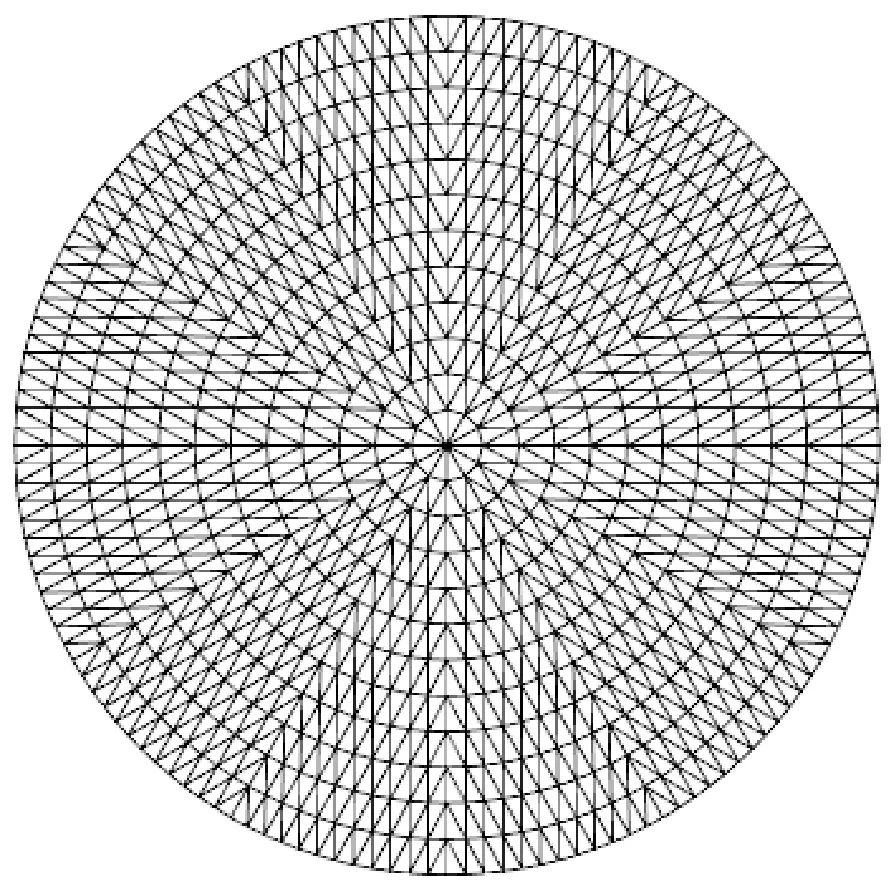
图2 管内成像区域剖分图Fig.2 Dissection diagram of the in-pipe imaging field

本文对4种典型流型进行了辨识研究,分别为:核心流、环流、高位层流及低位层流,如图3所示。通过ECT仿真软件包对每种流型设置200个样本,并计算其对应的电容测量值,4种流型共计800个样本。本文基于随机的思想建立4种流型,即核心流随机生成流型半径r;环流随机生成环流宽度d;高位层流和低位层流分别随机生成液位高度h1和h2,以使流型具有统计意义上的代表性。

图3 典型流型Fig.3 Typical flow regime

3.2 流型辨识

从800个仿真样本中随机选取600个样本作为PSO-ELM算法的训练样本,剩下的200个样本作为测试样本。各样本对应的66个仿真电容值作为网络输入,流型类型作为网络输出,4种流型对应络输出值分别为1,2,3及4。

训练过程中,不断增加PSO-ELM隐层节点以观察其预测效果,并与相同隐层节点数下ELM算法的预测结果进行比较；训练结束后,使用测试样本对其辨识效果进行检验,其流型正确辨识率结果如图4所示。

图4 测试样本的流型正确辨识率Fig.4 Correct identification rate for test samples

由图4可见,PSO-ELM算法在2个隐层节点时,即可对4类流型进行100%正确辨识,而ELM算法在10个隐层节点时首次达到100%正确辨识,由此可见,PSO-ELM算法预测效果明显优于ELM算法;此外,当PSO-ELM算法的隐层节点数从2增加到15的过程中,其正确辨识率均为100%,而ELM算法正确辨识率出现上下波动。

综上所述,PSO-ELM与ELM算法相比,可在更为简洁的网络结构下,获得更为稳定及更高精度的辨识效果。

4 基于PSO-ELM的流型参数预测

在流型辨识的基础上,基于PSO-ELM算法进行

了流型位置参数的预测,位置参数为:核心流半径r;环流的流体宽度d;高位层流及低位层流的液位高度h1及h2。

本文将4种流型对应的电容值以及流型位置参数分别作为各种流型参数预测网络的输入和输出,随机选取每种流型的150个样本作为训练样本,剩下的50个样本作为测试样本。本文选取均方误差(MSE)和决定系数(R2)作为流型位置参数预测的评价指标,其定义为:

(6)

(7)

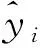
MSE越接近于0,表明预测参数越接近于实际流型参数；R2越接近于1,表明预测效果越好。

PSO-ELM在不同隐层节点数下各种流型位置参数预测效果如表1及表2所示。表中ELM算法在隐层节点数为N时记为ELM-N(如:ELM-1,ELM-2,…),PSO-ELM算法在隐层节点数为N时记为PSO-ELM-N(如:PSO-ELM-1,PSO-ELM-2,…)。

表1 不同隐层节点下的均方误差Tab.1 Mean Square Error of different hidden layer nodes

从表1和表2可知,PSO-ELM算法较ELM算法参数预测结果的MSE在隐层节点数大于1时相差1个量级;在相同隐层节点数下,PSO-ELM算法R2更接近1,表明PSO-ELM算法预测精度更高。为检验PSO-ELM及ELM算法的参数预测结果,对所研究的4种流型,分别随机选取5个样本,隐层节点数取为3,其预测结果如表3所示。由表3可知,在相同的隐层节点数下,PSO-ELM算法的参数预测结果相较于ELM算法预测结果更接近于实际值,其最大相对误差为5.24%。

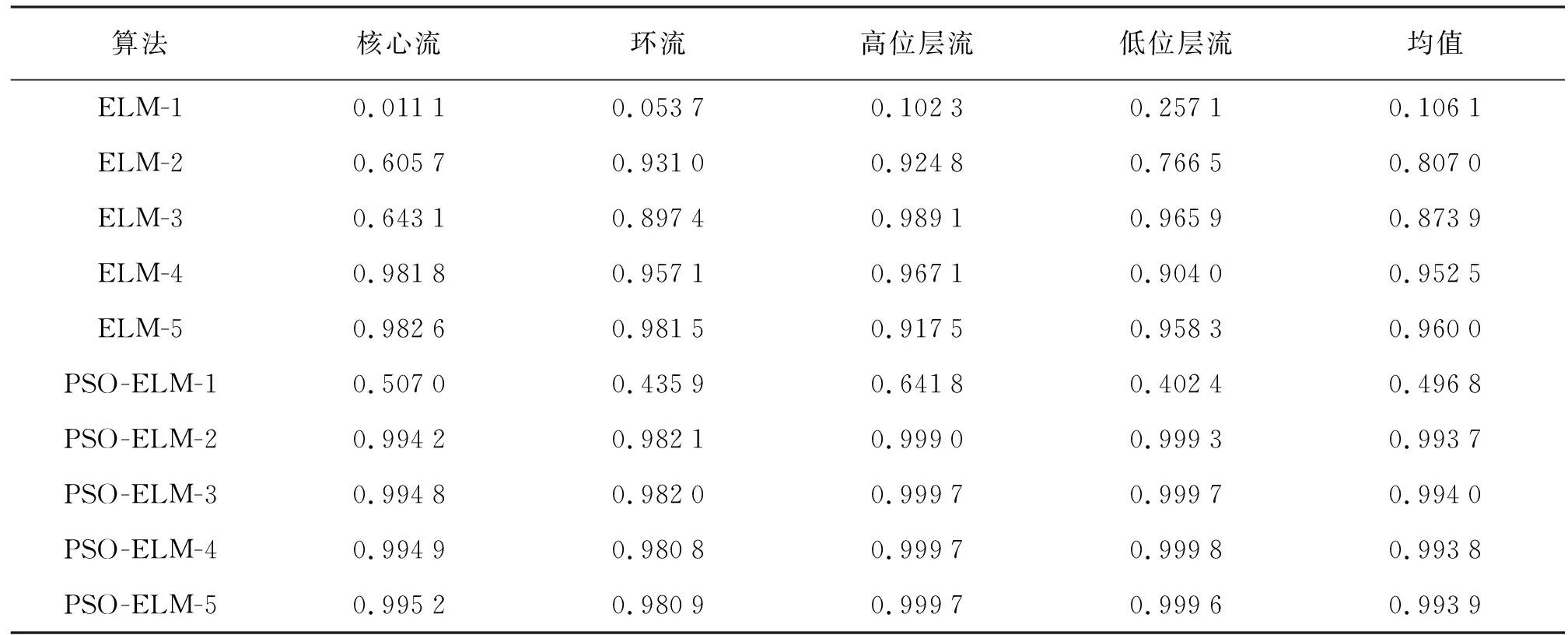
表2 不同隐层节点下的决定系数Tab.2 Determination coefficients of different hidden layer nodes

表3 预测结果Tab.3 Prediction results

5 结 论

1) 使用粒子群算法优化极限学习机和电容层析成像技术对4种典型流型进行流型辨识和特征预测,仿真实验结果表明:PSO-ELM算法较ELM算法可在更少的隐层节点下准确辨识流型及进行流型参数预测;

2) 本文以水平管4种典型流型为例,进行了基于PSO-ELM方法进行流型辨识与特征参数预测的初步研究,对于竖直、倾斜管流,从理论上来说,该方法同样适用;

3) 以中心流为例,隐层节点数为3时,PSO-ELM算法的流型辨识及流型参数预测时间分别为0.005 9 s及0.022 7 s。因此,该算法可以在线使用,实现流型及其参数的实时辨识及预测。

[参考文献]

[1] 张立峰. 压缩感知在电容层析成像中的应用 [J]. 北京航空航天大学学报, 2017, 43(11): 2316-2321.

Zhang L F. Compressed sensing application to electrical capacitance tomography [J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2017, 43(11): 2316-2321.

[2] 张立峰, 宋亚杰. 基于梯度投影稀疏重建算法的电容层析成像图像重建 [J]. 计量学报, 2019, 40(4): 631-635.

Zhang L F, Song Y J. Image Reconstruction for Electrical Capacitance Tomography Based on Barzilai-Borwein Gradient Projection for Sparse Reconstruction Algorithm[J].ActaMetrologicaSinica, 2019, 40(4): 631-635.

[3] Meribout M, Saied I M. Real-Time Two-Dimensional Imaging of Solid Contaminants in Gas Pipelines Using an Electrical Capacitance Tomography System [J].IEEETransactionsonIndustrialElectronics, 2017, 64(5): 3989-3996.

[4] 孔银. 电容层析成像技术图像重建算法的研究[D]. 哈尔滨:哈尔滨理工大学, 2017.

[5] 张立峰, 王化祥. 基于SVM及电容层析成像的两相流流型识别 [J]. 仪器仪表学报, 2009, 30(4): 812-816.

Zhang L F, Wang H X. Identification of two-phase flow regime based on support vector machine and electrical capacitance tomography technique [J].ChineseJournalofScientificInstrument, 2009, 30(4): 812-816.

[6] Huang G B, Zhu Q Y, Siew C H. Extreme learning machine: a new learning scheme of feedforward neural networks [J].IEEEInternationalJointConferenceonNeuralNetworks, 2004, 2: 985-990.

[7] Huang G B, Zhu Q Y, Siew C H. Extreme learning machine: Theory and applications [J].Neurocomputing, 2006, 70(1): 489-501.

[8] 何群, 王红, 江国乾, 等. 基于相关主成分分析和极限学习机的风电机组主轴承状态监测研究 [J]. 计量学报, 2019, 39(1): 89-93.

He Q, Wang H, Jiang G Q,etal. Research of Wind Turbine Main Bearing Condition Monitoring Based on Correlation PCA and ELM [J].ActaMetrologicaSinica, 2018, 39(1): 89-93.

[9] 吴忠强，尚梦瑶，申丹丹,等. 基于BSA-RELM的纯电动汽车锂离子电池SOC估计[J]. 计量学报, 2019, 40(4): 693-699.

Wu Z Q, Shang M Y, Shen D D,etal. Estimation of SOC of Li-ion Battery in Pure Electric Vehicle by BSA-RELM[J].ActaMetrologicaSinica, 2019, 40(4): 693-699.

[10] 毛羽, 毛力, 杨弘, 等. 改进人工蜂群优化的极限学习机 [J]. 传感器与微系统, 2018, 37(4): 116-120.

Mao Y, Mao L, Yang H,etal. Extreme learning machine optimized by improved ABC [J].TransducerandMicrosystemTechnologies, 2018, 37(4): 116-120.

[11] Chu Z, Ye M, Jing C. Adaptive reactionless control strategy via the PSO-ELM algorithm for free-floating space robots during manipulation of unknown objects [J].NonlinearDynamics, 2018, 91(2): 1321-1335.

[12] Chatterjee S, Sarkar S, Hore S,etal. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings [J].NeuralComputing&Applications, 2017, 28(8): 2005-2016.

[13] Bonyadi M R, Michalewicz Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review [J].EvolutionaryComputation, 2017, 25(1): 1-54.

[14] 刘彬, 赵朋程, 高伟, 等. 基于粒子群算法与连续型深度信念网络的水泥熟料游离氧化钙预测 [J]. 计量学报, 2018, 39(3): 134-138.

Liu B, Zhao P C, Gao W,etal. Prediction of Cement fCaO Based on Particle Swarm Optimization and Continuous Deep Belief Network [J].ActaMetrologicaSinica, 2018, 39(3): 134-138.

[15] 李婉华, 陈羽中, 郭昆, 等. 基于改进粒子群优化的并行极限学习机 [J]. 模式识别与人工智能, 2016, 29(9): 840-849.

Li W H, Chen Y Z, Guo K,etal. Parallel Extreme Learning Machine Based on Improved Particle Swarm Optimization [J].PatternRecognitionandArtificialIntelligence, 2016, 29(9): 840-849.

[16] 高斐, 李洪儒, 许葆华. 基于ICPSO优化的极限学习机在故障诊断中的应用 [J]. 中国机械工程, 2013, 24(20): 2753-2757.

Gao F, Li H R, Xu B H. Applications of Extreme Learning Machine Optimized by ICPSO in Fault Diagnosis [J].ChinaMechanicalEngineering, 2013, 24(20): 2753-2757.