基于主成分分析及多维高斯贝叶斯的超声流量计故障智能诊断方法

朱建新 , 吕宝林, 乔 松, 王溢芳, 陈嘉宏

(1. 合肥通用机械研究院有限公司,安徽 合肥 230031；2. 国家压力容器与管道安全工程技术研究中心,安徽 合肥 230031)

1 引 言

流程行业设备在长周期运行过程中,受部件之间、设备之间以及设备与工艺介质之间的耦合影响,发生的失效或故障十分复杂,故障一旦发生往往导致流程中断,因而行业对设备的可靠性具有很高的要求。传统的设备失效或故障诊断往往从机理出发,利用材料力学、结构力学、流体力学以及腐蚀理论等开展失效或故障的分析,这种方法对于结构单一、影响因素简单、失效或故障模式清晰的失效往往十分有效[1]。基于机理的分析方法在传统的设备失效或故障诊断中发挥了重要作用,如依据振动频谱分析转子可能发生的不平衡、不对中及磨碰等故障,依据润滑油成分分析设备可能的故障等[2],采用化学成分、力学性能、金相等分析设备的失效[3],采用动力学及振动响应分析方法研究转子-支承-机匣耦合系统碰摩故障、滚动轴承故障等[4～6]。然而随着设备复杂程度的提高,部件之间、设备之间、设备与工艺之间耦合关联,设备发生失效或故障往往受多种因素影响,在这种情况下设备主导失效或故障机理的分析需要设计、材料、制造、使用管理等多专业配合[1]。传统的以机理分析为主的故障诊断方法需要全面考虑这些相互影响,并在做大量简化的前提下选择部分主导因素开展分析,因而分析过程复杂且准确性难以保证。若将所有影响因素全部考虑在内又会因系统的复杂程度太高而无法求解。为解决这一问题,研究者将主要影响因素及其相互关系进行一定的简化后,提出了基于贝叶斯网络的可靠性分析方法[7,8]。贝叶斯网络是不确定知识表达和推理领域最有效的理论模型,该方法考虑了影响因素的相互关系后,以贝叶斯理论为基础开展故障的诊断,在一定程度上解决了复杂系统的可靠性分析与故障诊断难题。如将贝叶斯网络用于机械系统的剩余寿命预测,大型回转设备故障诊断,水电机组的振动故障诊断、机械设备转子系统的故障诊断等[9～13]。

贝叶斯网络通过建立表示事件之间因果关系的有向无环图,并利用一系列条件概率来分析事件发生的依存关系及可能性,因而应用贝叶斯网络时,首先要建立表示事件因(父节点)与果(子节点)之间的相互关系。实际应用时,若无法明确状态之间的因果关系,贝叶斯网络构建就存在困难,此外当存在多个影响因素时,影响因素之间的独立性也难以保证。

近年来随着数据科学的发展,将大数据分析方法用于多种影响因素耦合作用的设备故障分析与诊断已成为可能,该方法以发生失效的原始数据为基础,通过对数据背后的统计规律进行深入研究,分析影响因素与故障状态之间的相互关系,用概率分析方法判断在多种因素交互作用下的设备失效或故障可能性。与传统的方法相比,由于无需进行任何简化,避免了先入为主的主观因素可能带来的不足,对影响因素的独立性没有特殊要求,因而可以最大程度避免不必要的简化带来的问题。

在众多的大数据的分析方法中,通过贝叶斯理论把现象发生的可能性与原因(故障)联系起来,描述了设备故障诊断的一般规律,因而贝叶斯模型在实际设备的故障诊断中具有广泛应用[7]。依据样本的特点,贝叶斯又分为朴素贝叶斯、高斯贝叶斯等不同类型。本文采用多维高斯贝叶斯模型为基础,研究了模型在故障智能诊断中的应用,以公开发表的超声流量计诊断数据库为例,对方法应用流程及效果进行分析,并将分析结果与k-最近邻(k- nearest neighbors,KNN)聚类分析算法结果进行比较。

2 多维高斯贝叶斯分类模型及诊断方法

2.1 多维高斯贝叶斯分类模型

设备的故障诊断,是通过观测设备运行的特征来判断发生特定故障的可能性。通常设备发生故障时往往伴随一个或多个特征,其完全符合贝叶斯理论有关条件概率的描述：当设备发生Ck类故障模式时,该故障会使设备表现出若干特征,如壁厚的减薄、振动振幅、频率、流量或压力的变化等。当观测的对象具有N个特征时,用X表示N个特征构成的特征向量。则当设备有K个可能的故障模式时,可以计算出Ck故障模式下X中N个特征的先验联合分布概率：

(1)

当发生Ck故障模式时,对应特征X的先验联合分布概率P(X|Ck)最大。这样可以通过计算不同故障模式下特征的联合分布概率,概率最大时对应的故障模式即为最可能的故障模式。

对于特征X中任一子特征x,若特定故障模式Ck下的子特征x的条件概率密度函数服从参数为μ和σ的高斯分布,即：

(2)

则认为特定的失效模式下任一子特征服从高斯分布,相应地满足该条件的全部子特征组成的联合分布称为多维高斯贝叶斯分布。

对于一个包含N个特征,共有K种故障模式(或称为分类)的系统,对特定的分类Ck,全部子特征组成的联合分布概率密度函数为[14,15]：

(3)

采用极大似然估计方法可以估计N个特征同时发生时系统隶属于Ck故障模式的似然函数值：

lnL= ln (P(x1,x2,…,xN|Ck))=

(4)

对特定的故障模式,式(4)中 ln (|ΣK|)和Nln (2π)均为常数。

对特定的待检样本,可以通过多维高斯贝叶斯求解不同故障模式下全部特征的联合分布概率密度,概率密度越大表明发生该故障模式的可能性越大。这样就可以利用极大似然对设备的故障进行智能诊断,通过排序筛选设备最可能的失效或故障模式,从而为维护维修提供依据。

2.2 智能诊断算法流程

基于多维高斯贝叶斯分类模型,可以整理出相应的智能诊断算法流程如图1所示。

图1 基于多维高斯贝叶斯的智能诊断算法流程Fig.1 Flowchart of smart diagnosis method based on multivariate Gaussian Bayesian model

智能诊断流程主要包括以下几个步骤：

1) 数据集准备。设备的故障数据样本是多维高斯贝叶斯智能诊断方法的基础,要针对特定的研究对象,筛选所有与故障有关的参数做为特征,并标记特征所对应的故障分类作为数据集。数据的收集过程中可能会由于偶发因素(如传感器损坏)导致数据缺失,故需要对数据集进行完整性分析,舍弃特征数据缺失的样本,或采用一定的策略补充缺失的数据,形成结构化的数据。

2) 数据的降维与数据集划分。当样本数量较少而特征数量较多时,可能导致建立的协方差矩阵为奇异矩阵而无法求逆,此时需要对数据进行降维处理,降维的作用一是通过特定的变换,使各特征参数投影到正交空间上,确保变换后的特征相互独立;二是通过保留变换后方差最大的若干个特征,舍弃方差小的特征,来实现参数降维。常见的降维算法有主成分分析(primary component analysis,PCA),奇异值分解等。降维后的数据需要将数据集依据一定的比例分成训练集与检验集,训练集用于分析检验集用于检验。

3) 不同故障模式的多维高斯贝叶斯模型的建立。在训练集中将相同故障模式的特征分别筛出,依据第2.1节的分析方法建立各故障模式的多维高斯贝叶斯模型。

4) 模型的检验。将检验集中除故障模式外的特征数据分别用不同故障模式的多维高斯贝叶斯模型进行计算,计算得到的似然函数最大的故障模式即为诊断结果。将该诊断结果与检验集样本中实际故障模式进行比对,判断模型的准确性。

5) 降维模型修正与模型的输出。由于降维后的特征数少于原始特征数量,不可避免会导致表征设备故障信息的丢失,为避免降维对诊断结果的影响,需要适当调整降维深度,使诊断识别率达到最佳。当通过多次检验达到最佳的效果时,将模型参数固化下来,用于后续故障的智能诊断。

本文方法仅通过特征的先验联合分布概率来进行故障的诊断,诊断过程并未涉及复杂的机理分析,以及为开展机理分析所做的简化,当设备故障机理复杂但数据量大时,该方法可以较好地满足大数据条件下设备故障的智能诊断要求。

2.3 数据的PCA降维

若故障数据收集共有M个样本X=[x1,x2,…,xM]T,其中第i个样本的W个的特征数据为xi=(xi,1,xi,2,…,xi,W),则各特征的协方差矩阵Σ如式(5)所示,协方差矩阵反映了各特征之间的相互关系。

(5)

式(5)中μ=[μ1,μ2,…,μW]为全部W个特征的均值。

若存在矩阵A∈RW×W,使(X-μ)·A=y,且y的协方差矩阵Σy满足：

=AT·Σ·A=Λ

(6)

式中：Λ为对角阵,其对角线元素λi为一个大于0的数,则说明变换得到的y中各特征相互独立,λi越大表明y中第i个特征的方差越大,即数据的分散性越好。

式(6)中的变换矩阵A即为由协方差矩阵Σ的特征值所对应的特征向量(列向量)组成的矩阵。当将特征值由大到小排列,取全部特征值之和中一定比例的前N个特征值,并将对应的N个特征向量(列向量)组成新的变换矩阵B∈RW×N,则通过计算(X-μ)·B即可将全部样本中的特征参数由W维降为N维。

降维时特征值的比例越小,降维深度越深,则保留的特征值个数N越小,即降维后的维数越小,信息丢失的越多。

3 应用案例分析

3.1 数据库简介

超声波流量计是一种以速度差法为原理的非接触测量仪表,测量准确度高,广泛应用于石油、化工、冶金、电力、给排水等领域。实际使用中超声波流量计存在空气侵入、蜡沉积等故障,需要定期进行校准。在英国的石化等流程行业中超声波流量计使用量大,但校准成本高昂[17]。为避免设备过度检验与校准,英国研究机构采集了流量计相关参数并建立了设备健康数据库,拟采用机器学习方法开展流量计健康诊断。

图2 超声波流量计检测通道Fig.2 Test paths of ultrasonic flowmeters

本文使用的超声波流量计故障诊断数据库(Ultrasonic flowmeter diagnostics Data Set,http:// archive.ics.uci.edu/ml/datasets/Ultrasonic+flowme-ter+diagnostics)是由英国考文垂大学(Coventry University)和国家工程实验室(National Engineering Laboratory,TUV-NEL)采集,数据库由加州大学欧文分校提供[18]。该数据库收录了4类流量计共540个样本,4类样本中,B型流量计的样本数92个,故障分类包括无故障(Healthy)、气体侵入(Gas injection)及蜡沉积(Waxing),C型流量计的样本数181个,故障分类除上述3种外,还包括安装影响(Installation effects)故障模式。2个子数据库中检测的项目分别如表1、表2所示。

利用多维高斯贝叶斯模型,本文对两类超声波流量计开展健康状态智能诊断。并利用k-最近邻(KNN)聚类分析工具,对2种分析方法的效果进行了比对。

表1 B型流量计故障诊断检测项目Tab.1 Test items for failure diagnosis of type B flowmeter

表2 C型流量计故障诊断检测项目Tab.2 Test items for failure diagnosis of type C flowmeter

3.2 数据预处理

超声波流量计故障诊断数据库是一个标准的结构化数据库,数据中不存在缺失数据,但数据库中原始的特征数分别为51和43个,多数特征存在明显的相关性,如4个通道中通道两端信号强度、信号质量,通道内流速与声速等。由于数据库的样本数偏少,仅为92和181个,为避免特征的协方差矩阵为奇异矩阵带来的求解困难,需要对样本数据进行降维处理,剔除相关的因素。

为更好地检验诊断效果,对样本进行随机排列后采用相同的方法进行10次不重复的诊断,相同的数据同时利用开源的聚类分析工具Scikit-learn中的KNN聚类分析算法进行诊断,并对结果进行比对。

3.3 诊断分析结果及比较

利用本文提出的方法及流程,对超声波流量计进行故障智能诊断。B型和C型流量计分别保留70.0%和99.7%的特征值进行降维,在全部样本中选择70%(B型64个,C型126个)用于训练,30%(B型28个,C型55个)用于检验,2种诊断方法得到的结果如表3所示。

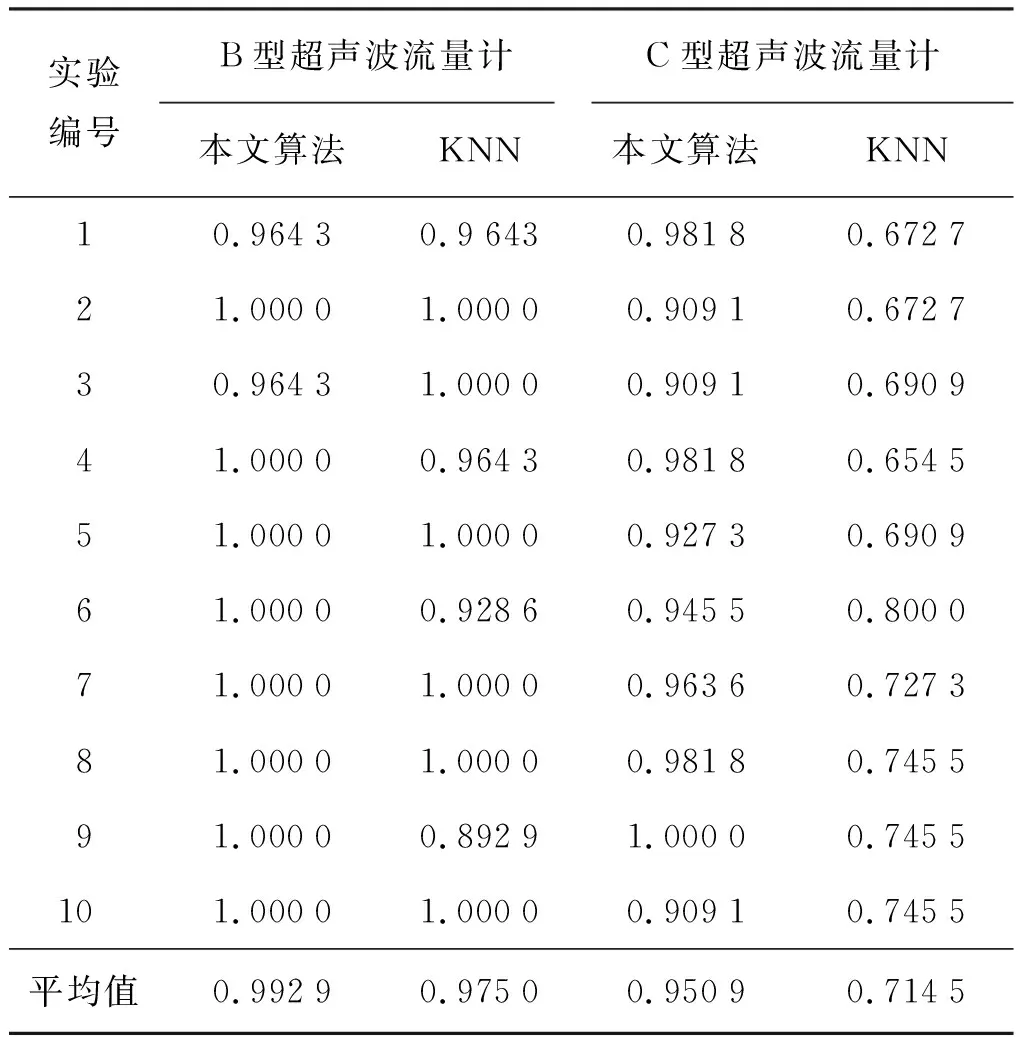
表3 流量计的检验结果Tab.3 Test results of flowmeters

为分析数据特征及降维深度对诊断结果的影响,采用不同的PCA降维策略,对B型和C型流量计进行诊断分析,得到结果如图3所示。图中可以发现B型流量计和C型流量计的诊断结果存在较大区别。对B型流量计采用PCA降维后,降维时特征值保留比例由0.4上升至0.9时,本文算法的诊断识别率98.5%附近波动,总体较佳但进一步增加特征值的保留比例会使维数增加过多,反而使识别率有所降低。而对于KNN算法,提高PCA降维特征值保留比例时,正确识别率会发生显著下降。C型流量计样本数量相对较多,当特征值保留比例由0.9上升至0.999时,本文算法计算得到的识别率显著增加,特征值保留比例达到99.9%时全部55个待检样本共550次诊断的故障识别率为96.9%,这一数据明显高于KNN聚类分析75.3%的诊断结果。

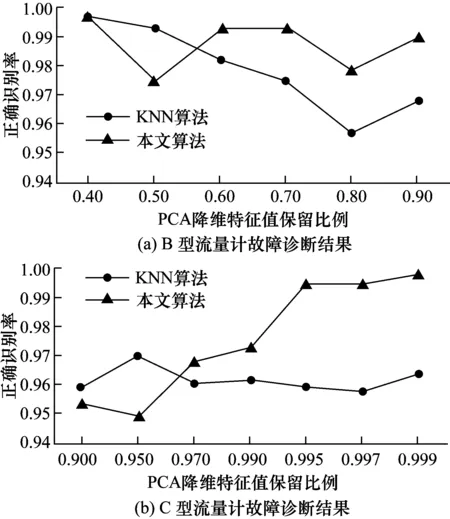
图3 两型流量计的PCA降维深度对故障识别率的影响Fig.3 Influence of PCA dimensionality reduction depth on failure diagnosis rate for two types of flowmeters

4 结 论

1) 提出了基于多维高斯贝叶斯的设备故障智能诊断流程,将该方法用于某超声波流量计的故障智能诊断,故障的正确识别率达到95%以上,该诊断效果总体优于k-最近邻(KNN)聚类分析算法;

2) 多维高斯贝叶斯分类算法克服了复杂设备系统故障诊断分析中需要对故障模式及影响进行机理研究,对耦合影响因素进行简化分析等不足,可将全部影响设备失效或故障的因素考虑在内,避免了为开展机理分析需要进行简化带来的不足;

3) 用多维高斯贝叶斯方法进行设备的故障诊断时,需要综合考虑样本及特征的数量、特征与失效或故障的相互关系,可以通过分析选择恰当的降维深度,以达到最佳的诊断效果;

4) 样本中不同特征对故障识别率的影响存在较大区别,应用降维技术进行分析时,不同的降维深度可能对诊断结果产生较大影响。由于PCA降维后的复合特征与初始特征存在一定的线性关系,如何利用复合特征来分析原始特征对诊断结果的影响,这是后续值得进一步开展的研究方向。