联想 等效 拓展 建模
——以“带电小球在复合场中的运动”为例
刘万强 肖梦军
(湖北省松滋市第一中学,湖北 松滋 434200)
1 问题
如图1所示,匀强电场的场强大小为E,与水平方向的夹角θ=30°,电场中有一质量为m、电荷量为q的带电小球,用长为L的绝缘细线悬挂于O点,当小球静止时,细线恰好水平。现用一外力将小球缓慢拉到竖直方向的最低点,然后将小球由静止开始释放,求:
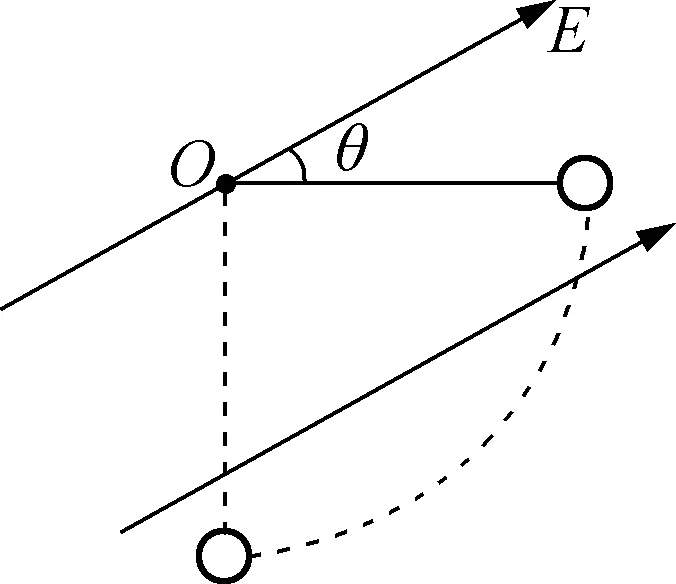
图1
(1) 小球在何处速度最大?最大速度为多少?
(2) 小球向右运动,最远处在哪里?
(3) 若小球能做完整的圆周运动,小球在运动过程中最小速度是多少?
速度最大(动能最大)的点、向右能够运动到达的最远处(动能为零)和做完整圆周运动等问题涉及的主要是能量问题,那如何分析在这种多场并存的复合场中的运动呢?我们会联想到小球只在重力场中的圆周运动。
2 联想
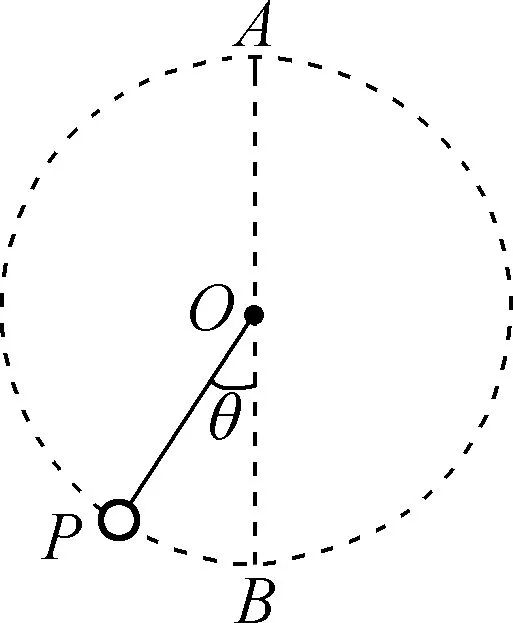
图2
如图2所示,细绳一端固定于O,另一端固定一小球,让小球在竖直平面内做圆周运动。现将小球从图示位置P由静止释放,细绳与竖直方向成夹角θ,求:
(1) 小球在何处速度最大?最大速度为多少?
(2) 小球向右运动,最远处在哪里?
(3) 若小球能做完整的圆周运动,小球在运动过程中最小速度是多少?

联想到小球只在重力场中的圆周运动,关注小球的动能和势能,可追溯到最简单的能量与圆周运动相结合的模型的源头。需重点关注小球的重力势能极值对应的高度位置:(1) 小球位于最高点时,动能最小、势能最大、绳中张力最小,绳子在此处不松弛是保证小球做完整圆周运动的充要条件;(2) 小球位于最低点时,动能最大、势能最小、绳中张力最大,绳在此处最易断裂。
假设小球只在匀强电场中运动,又如何处理呢?我们不妨进行类比分析。
3 等效
如图3所示,在光滑绝缘水平面上放置一质量为m、电荷量为q的带正电小球,小球系在长为L的绝缘细线上,线的另一端固定在O点。整个装置置于大小为E的匀强电场中,电场方向与水平面平行且沿OA方向。现将小球从OA左边与OA垂直的位置静止释放,求:

图3
(1) 小球在何处速度最大?最大速度为多少?
(2) 小球向右运动,最远处在哪里?
(3) 若小球能做完整的圆周运动,小球运动过程的最小速度是多少?
将电场力Eq等效成重力场中的重力mg,那么A处于最低等势面上,相当于重力场的最低位置,可以将小球的电势能与重力势能相类比,则在A处电势能最小,速度最大,小球绕等效最低点两边对称摆动,向右可摆到OA右边以及与OA垂直的位置。如能做完整的圆周运动,恰好过等效最高点(即A关于O的对称点),此处电势能最大,动能最小,绳子拉力最小。
重力和电场力对带电小球的运动都有影响,又该如何处理呢?我们不妨分两力共线和不共线两种情况来拓展研究。
4 拓展
4.1 重力和电场力在同一直线上
如图4所示,在长为L的丝线的一端拴一质量为m、电荷量为q的带正电小球,另一端连在水平轴O上。丝线拉着小球可在竖直平面内做圆周运动,整个装置处在竖直向上的匀强电场中,电场强度大小为E,且电场力Eq大于重力mg。现将小球拉到与轴O在同一水平面上的A点,然后无初速度地将小球释放。求:

图4
(1) 小球在何处速度最大?最大速度为多少?
(2) 小球向右运动,最远处在哪里?
(3) 若小球能做完整的圆周运动,小球在运动过程中的最小速度是多少?
将电场力Eq和重力mg进行合成,得到合力F=Eq-mg(称为等效场力),其方向向上,B处于等效场的最低等势面上,相当于重力场中的最低处,把小球的电势能和重力势能之和(称为等效场势能)与重力势能相类比,则B处等效场势能最小,速度最大,B成为等效最低点,小球绕等效最低点两边对称摆动,向左可摆到A关于O的对称点。如能做完整的圆周运动,恰好过等效最高点(即B关于O的对称点),此处等效场势能最大,动能最小,丝线拉力最小。
4.2 重力和电场力不在同一直线上
如图5所示,在水平方向的匀强电场中,在一根不可伸长的绝缘细绳的一端连着一个质量为m、电荷量为q的带正电小球,另一端固定于O点,把小球拉起直到细绳与场强方向平行,然后无初速度释放,则小球沿圆弧做往复运动。已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ,求:

图5
(1) 小球在何处速度最大?最大速度为多少?
(2) 若小球能做完整的圆周运动,小球在运动过程中的最小速度是多少?
如图6所示,将电场力Eq和重力mg进行合成,得到合力F(称为等效场力),其方向为斜向右下方,过圆心画出沿合力F方向的直线,与圆轨迹交于点A、B两点(图7),用F等效替换仅在重力场中运动的小球受到的重力mg,那么A处于等

图6

图7
效场的最低等势面上,相当于重力场的最低处,将小球的电势能和重力势能之和(称为等效场势能)与重力势能相类比,则A处等效场势能最小,速度最大,A成为等效最低点,小球绕等效最低点两边对称摆动。若带电小球能做完整圆周运动,恰好过等效最高点(即A关于O的对称点B),此处等效场势能最大,动能最小,丝线拉力最小。
5 建模
研究小球在重力场和电场并存的复合场中的圆周运动时,通过联想、等效到拓展类比,建立了以等效场、等效场力、等效场加速度、等效最高(最低)点和等效场力势能等概念组成的等效场模型,分析带正电的小球在仅有重力场、仅有电场、重力场和电场并存三种情况下的圆周运动,比较结果如表1。

表1
如图8所示,将原题中的电场力Eq和重力mg进行合成,得到合力F(称为等效场力),其方向为水平向右,过圆心画沿合力F方向的直线,与圆轨迹交于点A、B两点(图9),用F等效替换仅

图8

图9
在重力场中运动的小球受到的mg,那么A处于等效场的最低等势面上,相当于重力场的最低处,将小球的电势能和重力势能之和(称为等效场势能)与重力势能相类比,则A处等效场势能最小,速度最大,A成为等效最低点,小球绕等效最低点对称摆动,即从空间最低点运动到空间最高点。若小球能做完整圆周运动,要能恰好过等效最高点(即A关于O的对称点B),此处等效场势能最大,动能最小,细线拉力最小。
6 结语
带电小球在等效场中的圆周运动是高中物理的重要模型。从物理观念来看,等效场模型涉及相互作用观、运动观和能量观;从科学探究来看,探究等效场中的场力、加速度、等效最高(最低)点等,通过发现、联想、推理等,循序渐进,深入探究;从科学思维来看,需要综合运用类比、等效、拓展、建模等思维方法;从科学态度与责任来看,通过对小球圆周运动的深入探究,有利于学生认识科学本质,形成正确的科学态度和责任感。

