圆锥摆模型中双球问题的探讨

朱 挺

(江苏省启东中学,江苏 南通 226200)

圆锥摆模型是高中物理中常见的一类模型，是在一根质量和伸长不计的细线下系一个可以视为质点的摆球，在水平面内做匀速圆周运动。摆球受竖直向下的重力和沿摆线方向的拉力作用，两个力的合力提供了摆球做圆周运动的向心力。

由基本的圆锥摆模型衍生出的双球问题是该模型中较复杂的一类问题，需要针对摆线倾角和摆长的特点，结合受力规律进行综合分析。

1 等倾双球问题

例1：如图1所示,质量相等的甲、乙两个小球,沿光滑玻璃漏斗内壁做水平面内的匀速圆周运动,甲在乙的上方,则它们运动的( )。

图1

A. 向心力F甲>F乙

B. 线速度v甲>v乙

C. 角速度ω甲>ω乙

D. 向心加速度a甲>a乙

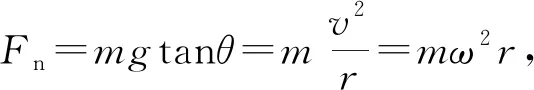
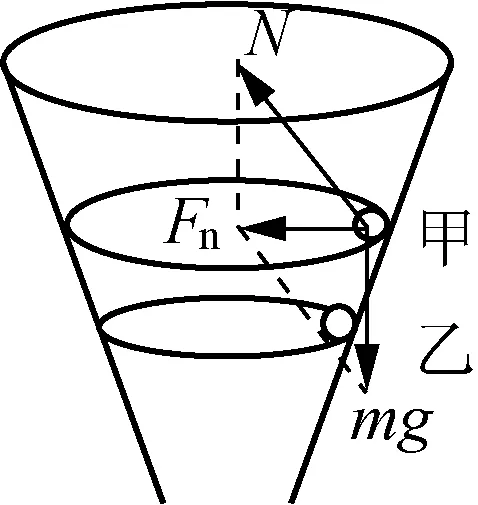
图2

由于两小球做圆锥摆运动时“摆线”的倾角相等，所以小球的受力方向一致，向心加速度的大小相等，这是解决问题的关键，再运用圆周运动的向心力公式来求得线速度、角速度等。

2 等高双球问题

例2：如图3所示，两根长度不同的细线下面分别悬挂着小球,细线上端固定在同一点,若两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,则两个小球在运动过程中的相对位置关系示意图正确的是( )。

图3

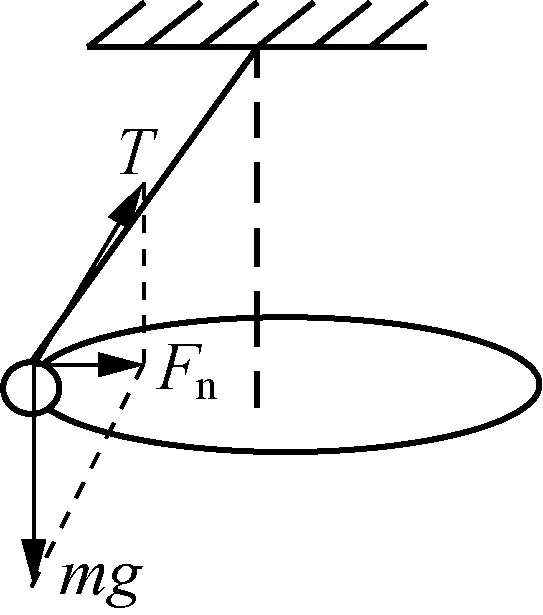
图4

在等高问题中，由于角速度相等这一前提条件，虽然两球的摆长和摆线的倾角不同，通过分离变量的方法，不难发现悬点到轨道平面等高的这一隐藏结果。

3 等长双球问题

例3：内壁光滑的半球形碗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着内壁分别在如图5所示的水平面内做匀速圆周运动,则( )。

图5

A. 球A的线速度等于球B的线速度

B. 球A的角速度大于球B的角速度

C. 球A的向心加速度小于球B的向心加速度

D. 球A对碗壁的压力等于球B对碗壁的压力

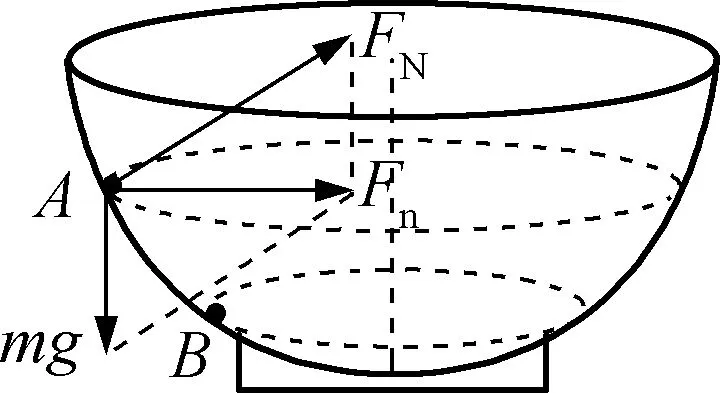
图6

本题中的两球的运动更具一般性，所以在处理问题时，还是从受力分析出发，在摆长相同的情况下，寻找相关物理量与倾角的关系，从而找到解决问题的突破口。

4 临界双球问题

例4：如图7所示,半径为R的半球形容器固定在水平转台上,转台绕过容器球心O的竖直轴线以角速度ω匀速转动,质量不同的小物块A、B随容器转动且相对器壁静止,A、B和球心O点连线与竖直方向的夹角分别为α和β,α>β，则( )。

图7

A.A的质量一定小于B的质量

B.A、B受到的摩擦力可能同时为零

C. 若A不受摩擦力,则B受沿容器壁向上的摩擦力

D. 若ω增大,A、B受到的摩擦力可能都增大

图8

若继续增加ω，则摩擦力方向将会反向。在竖直方向上有：FNcosα+fsinα=mg；在水平方向上有：FNsinα+fcosα=mω2Rsinα，且f随着ω的增加而增加，直至A与容器发生相对滑动。

读者可以自行计算A与容器发生相对运动的临界角速度，可见本题答案与A、B的质量无关，故选项A错误；由于倾角不同，A、B两物体的临界角速度不同，所以选项B错误；因为α>β，所以当A的临界角速度大于B，A不受摩擦力时，B所受摩擦力沿容器壁向下，所以选项C错误；当角速度大于A的临界角速度时，则A、B摩擦力均沿容器壁向下，且随着角速度的增加而增加，选项D正确。

本题从运动小球受力分析出发，列出相关的方程，找到临界点出现的规律，从而全面、直观地分析整个运动过程。

综上所述，在圆锥摆模型中的双球问题的处理上，我们应该抓住问题的主要特征，从受力分析出发，建立相关物理量与摆角、摆长之间的联系，找到解决问题的办法。