极限海况下6 MW单柱型浮式风力机耦合动力响应

阳 杰，何炎平，孟 龙，赵永生，吴浩宇

(上海交通大学 海洋工程国家重点实验室；高新船舶与深海开发装备协同创新中心；船舶海洋与建筑工程学院，上海 200240)

目前，经济发展对能源的需求越来越大，而传统的化石能源属于不可再生资源，随着不断开采、使用，其储藏量也在不断减少.世界正在面临巨大的能源危机，风能作为可再生能源，越来越受到重视.如今陆上风能已经被越来越多的国家逐渐开发使用，成为了重要的可再生能源之一[1].随着我国海洋强国战略的提出，人们对于海洋能源的关注日益加强，海上风能也越来越受到人们的重视.在陆上风能开发技术日益成熟的条件下，海上风力发电技术能够进一步减少我们对于化石能源的依赖，使得经济发展与环境保护更加协调.2018年，全球新建多个大型海上风电项目，这些新建的海上风电项目融资达到178亿元左右.伴随着全球海上风电项目的展开和新型市场的兴起，海上风能正逐渐向世界主流能源迈进.

浮式风力机(FOWT)是海上风能开采的重要途径，主要有驳船型(Barge)、半潜型(Semi-submersible)、张力腿型(TLP)和单柱型(Spar)几种形式[2].在大于50 m的海域采用Spar型浮式基础作为支撑能够有效降低风力发电成本.目前，已经有很多学者对浮式风力机进行了研究工作.针对5 MW风力机，Jonkman等[3]设计了以Spar平台作为浮式基础的OC3-Hywind，并且通过其开发的“气动-水动-伺服-弹性”软件FAST对风力机动力响应进行了时域耦合计算[4].Jonkman 等[5]还对驳船型、张力腿型和OC3-Hywind风力机进行了模型开发和载荷分析比较.除此之外，国内的学者也对浮式风力机做了不少研究，Zhao等[6]对5 MW TLP型浮式风力机进行了时域动态全耦合分析，数值分析结果表明，该TLP型风力机具有较好的水动力性能.唐友刚等[7]针对5 MW浮式风力机设计了1种Spar型浮式平台，并对其进行了频域分析.马钰[8]针对5 MW OC3-Hywind进行了时域全耦合动力响应计算，并且提出了浮式风力机在水池中进行模型试验的思路.杜炜康等[9]、郭子伟等[10]、陈哲等[11]对浮式风力机的模型叶片设计方法进行了计算研究，优化了模型叶片的设计方法.为了拓展Spar型浮式风力机的适用水深范围，Meng等[12]开发了一型适用于工作在100 m水深海域的6 MW单柱型浮式风力机，并对该风力机进行了时域耦合响应分析计算研究[13].虽然国内外学者做出了大量的研究工作，但是大部分研究只采用了数值模拟分析，只有少数的学者对风力机进行了试验研究，并且试验数据不公开且不全面.此外，已有的大部分试验都是基于5 MW浮式风力机进行的，对于6 MW Spar型浮式风力机涉及很少.然而，要大规模开发和有效利用风能，风力机向着更大的兆瓦级发展是必然趋势，这就意味着风力机需要走向大型化.与5 MW浮式风力机相比，随着单机功率的提高，6 MW风力机风轮直径更大，塔架的尺度也更大，流固耦合问题更加显著.故此，在恶劣工作条件下和极端天气状况下，风力机塔筒与浮式基础的结构稳定性和安全性研究更为重要.但是，目前专门针对浮式风力机极限海况的试验分析还很少.

为了补充以上研究内容的空缺，本文以新型 6 MW Spar型浮式风力机[12]为研究对象，在极限海况下对风力机进行了模型试验，得到了风力机的六自由度运动响应、锚泊系统的受力情况以及风力机危险受力点的受力情况.同时，运用数值仿真软件对风力机在极限海况下的六自由度运动特性及系泊系统响应特性进行了时域全耦合分析，并且对数值仿真的可靠性进行了分析验证.对风力机的试验结果和数值模拟结果进行了时域和频域分析，预报了风力机的极限载荷，为结构强度计算提供必要的理论依据和计算参数.研究极限海况风力机动力响应所采用的试验方法、数值模拟方法、极限载荷分析方法以及模型试验的数据对后续研究、工程设计和实际运行等均有较多参考意义.

1 浮式风力机基本参数

1.1 浮式风力机整体模型概述

6 MW Spar型浮式风力机[12]主要由风轮系统、塔筒、Spar平台以及锚泊系统组成，其示意图如图1所示.锚泊系统采用3根互相成120°的悬链线组成，锚链与Spar平台采用Delta-line形式连接[14].浮式风力机试验模型的缩尺比λ=65.3，试验模型如图2所示，试验主要参数见表1，更详细的参数可参见文献[12].

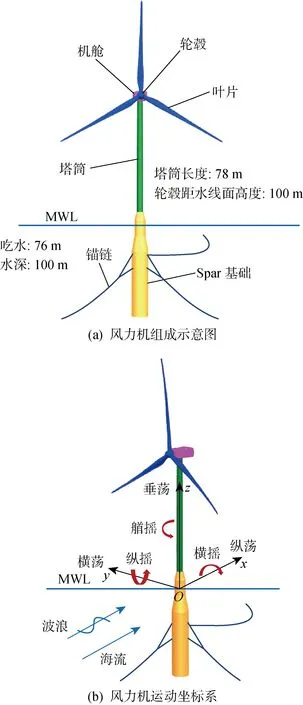
图1 6 MW Spar型浮式风力机示意图Fig.1 Schematic of 6 MW Spar-type FOWT

图2 浮式风力机水池试验模型Fig.2 FOWT model for basin test

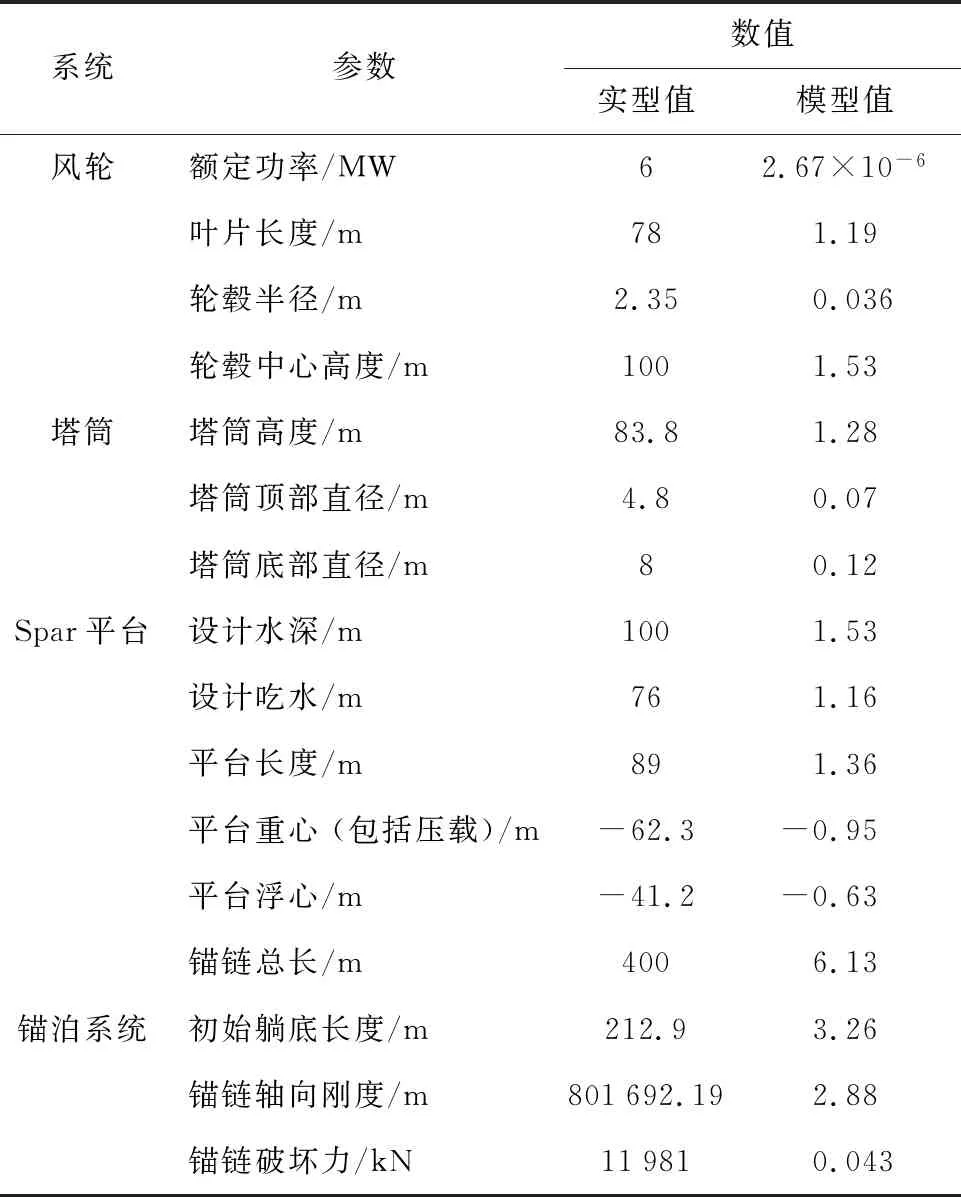
表1 浮式风力机主要参数Tab.1 Main characteristics of FOWT

1.2 极限海况风环境模拟

由于空气密度随高度、温度和湿度的变化而变化以及海面属于粗糙平面的原因，平均风速沿着垂直高度方向变化.实际应用中，平均风速沿高度的变化规律可用对数函数或幂函数来描述.幂函数关系式为

(1)

式中：z为海平面以上高度；Vm(z)为海平面以上高度z处的平均风速；h为海平面以上参考高度，根据挪威船级社规范，一般h取为10 m；Vm(h)为海平面以上参考高度h处的平均风速；系数α与海平面粗糙度、测量风速的时长和距地表高度有关，典型取值范围为0.1～0.2.

本文采用Kaimal风谱表示风速的脉动部分，其功率谱密度为

(2)

式中：ω为频率；σ为风速的标准差；L为特征长度.

1.3 极限海况海流模拟

模型风力机试验在上海交通大学海洋深水试验池进行，水池主体长50 m、宽40 m、深度由可升降式假底控制在0～10 m.极限海况试验中极限海况采用的造流系统为外循环分层造流系统，可以模拟垂向流速剖面深水流，表层流速最高可达0.4 m/s，速度水流速度沿水深的变化采用Near-Surface模型描述，如图3所示，Near-Surface模型公式为

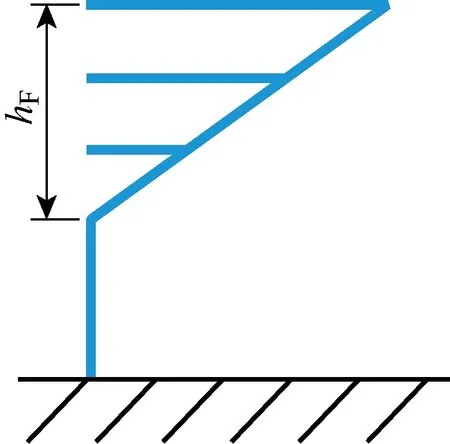
图3 Near-Surface模型Fig.3 Model of Near-Surface

(3)

式中：Vc(d)为水流速度；d为水线面以下深度；V0为水线面处水流速度(表层流速)；hF为参考深度.

图4所示为极限海况下海流速度测量值与目标值.可以看出，海流速度测量值与目标值吻合良好，符合模型试验要求.

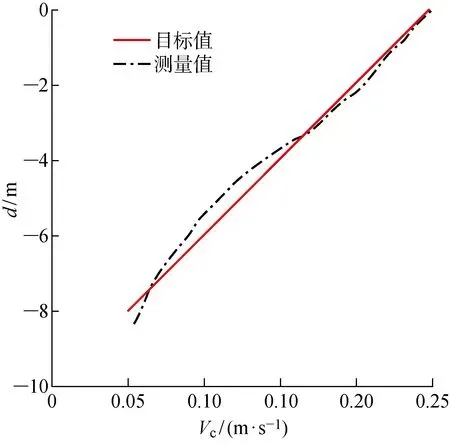
图4 极限海况下海流测量值与目标值Fig.4 Measurement values and target values under extreme condition

1.4 极限海况波浪环境模拟

试验中海域模拟采用北海海域的海洋环境.基于该海洋环境对浮式风力机在极限海况下的动力响应进行试验，模拟采用 50年一遇风浪流条件，波浪模拟选用双参数JONSWAP谱，波浪谱密度为

(4)

式中：h1/3为有义波高；T1为谱峰周期；γ为谱型参数.

图5和图6分别给出了极限海况下的波浪测量谱和目标谱的比较以及水池试验中极限海况下的波浪时历曲线，图中f为波浪频率.可以看出，水池试验中模拟的极限海况不规则波的精度非常高，符合模型试验要求.

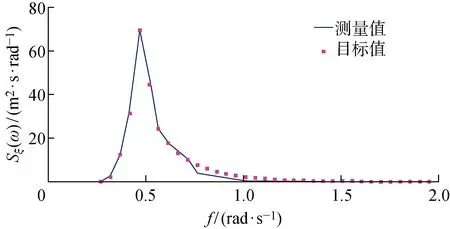
图5 极限海况下波浪测量谱与目标谱Fig.5 Target and measured wave spectrum under extreme condition

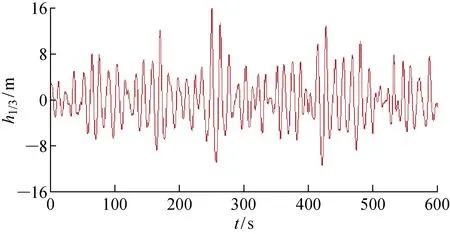
图6 极限海况下的波浪时历曲线Fig.6 Wave height history curve under extreme condition

表2给出了极限海况的主要环境条件.在极限海况下，风力机的风轮将处于停机状态，此时桨距角为90°，风载荷对风力机作用非常小，可以忽略不计，风力机的动力响应主要受到波浪载荷和流载荷的影响，所以试验时采用波浪载荷和流载荷同时作用进行试验.

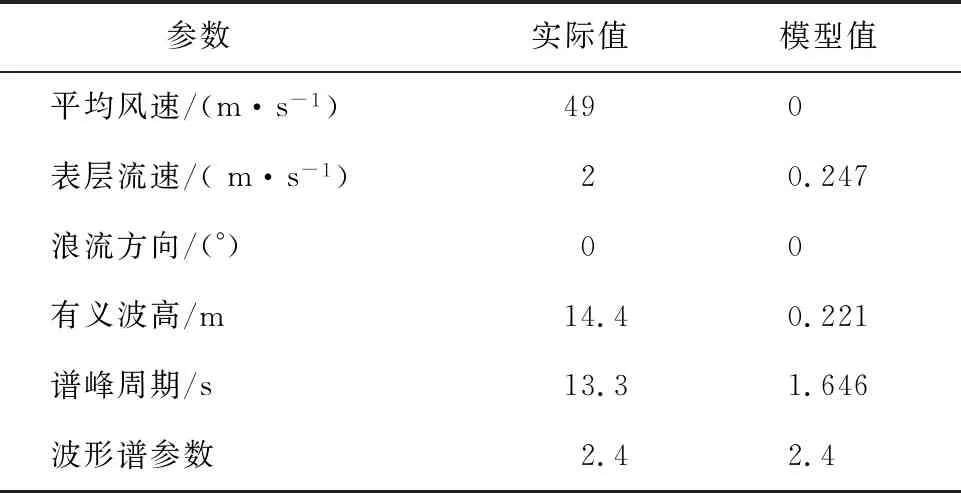
表2 极限海况环境条件主要参数Tab.2 Main environmental parameters of extreme condition

1.5 相似准则

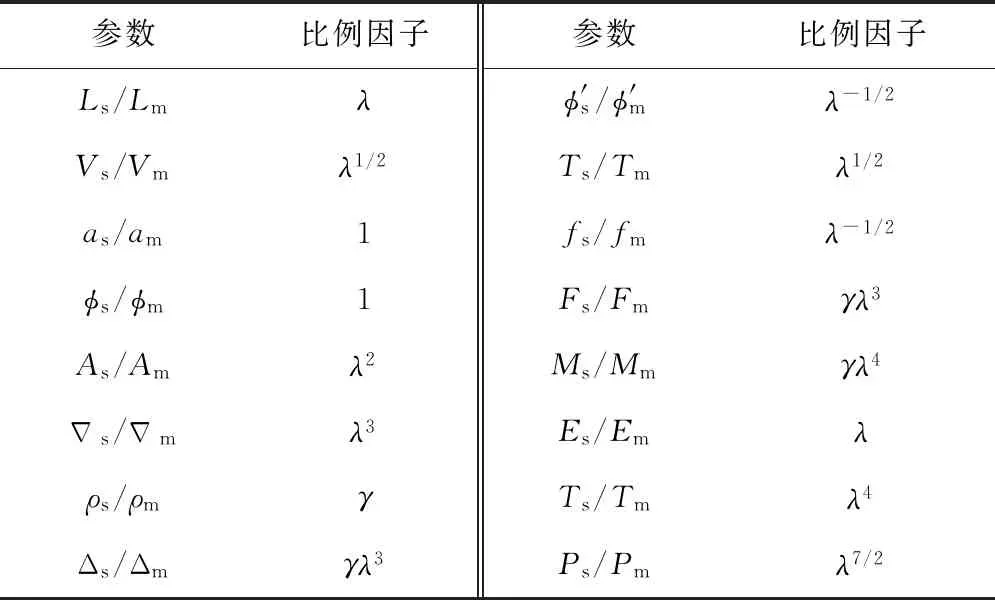
表3 模型与原型风力机系统之间的比例因子Tab.3 Scaling factors between model and prototype wind turbine system

2 数值模型

2.1 运动方程

数值模拟分析采用“气动-水动-伺服-弹性”软件FAST，FAST是由美国国家可再生能源实验室(NREL)开发的浮式风力机数值模拟软件，由AeroDyn、HydroDyn、MoorDyn、SevroDyn和BeamDyn等模块组成，可以建立浮式风力机耦合时域计算模型.

风机、塔架、平台以及锚链运动的完整耦合非线性时域运动方程为

(5)

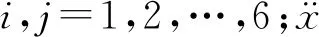
2.2 水动力载荷

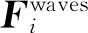
(6)

(10)

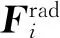
2.3 锚链力

锚链力的计算采用有限元(FEA)模型，锚链简化为离散的弹性细长杆模型[15].杆模型的有限元方程采用1个全局坐标系，如图7所示.变形后的锚链中心线由图7中位置向量曲线r(s,t)表示，其中s为弧坐标,q为锚链单位长度上的受力，M为锚链单位长度上的弯矩，F为沿着锚链中心线的合力，箭头方向为各受力方向.用r′表示单位切向量(r(s,t)对弧度的微分)，r″表示单位主法向量，r′×r″表示单位副法向量.

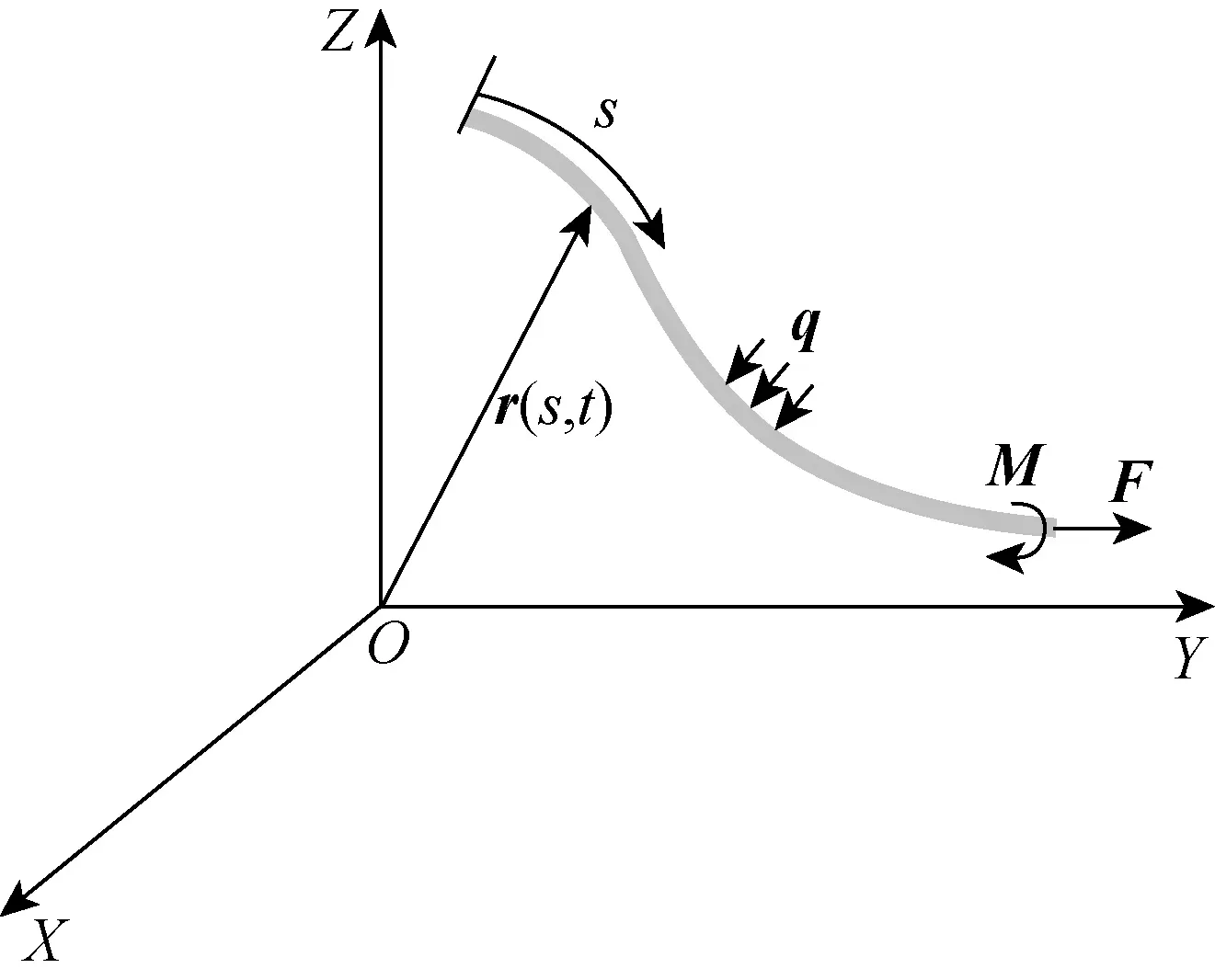
图7 细长杆模型坐标系Fig.7 Coordinate system for slender rod

根据牛顿第二定律，得出锚链单位长度上的力平衡方程：

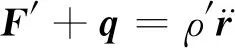
(11)

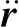
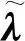
q=W+Fs+Fd

(14)

Fd可以用Morison方程表示为

(15)

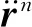
将式(12)～(15)代入式(11)可以得到锚链的运动控制方程：

(16)

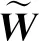
(17)

式中：A′为锚链截面面积.

杆模型的控制方程由式(16)、(17)共同组成.由于控制方程是非线性的，很难得到解析解，所以利用有限元方法来求解弹性杆的运动微分方程，上述控制方程可以通过一系列代数方程进行求解：

(18)

(19)

3 耦合动力响应试验结果对比分析

为了便于分析和比较，以下所有的数值模拟和模型试验数据都已经根据相似准则(表3)转换为实尺度数据.在进行极限海况试验前，先对风力机进行了静水衰减试验，得到了风力机的六自由度的固有周期，如表4所示.可以看出，由试验得到的以及由数值模拟得到的风力机六自由度运动固有周期得到的吻合良好.

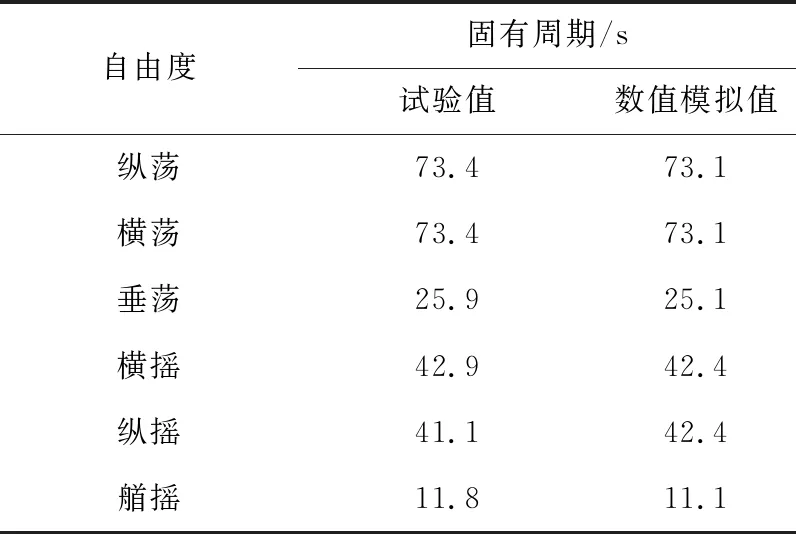
表4 浮式风力机六自由度运动的固有周期Tab.4 Natural period of six degrees of freedom of FOWT

3.1 纵荡运动

通过数值模拟和模型试验，得到了纵荡响应时历曲线以及纵荡功率谱，如图8所示.图中，ζ为运动响应值.可以看出，对于纵荡运动，存在3个能量峰值点，分别对应风力机的纵荡固有周期、纵摇固有周期以及波浪周期.纵荡功率谱在纵荡固有周期处出现最大的能量峰值，这说明在极限海况下，纵荡运动的能量主要集中在低频运动.风力机纵荡功率谱在纵摇的固有周期处出现峰值，表明纵荡和纵摇存在一定的耦合作用.纵荡功率谱在波浪的周期处出现了明显较大的峰值，这说明了波浪载荷对风力机纵荡运动影响较大.除此之外，数值模拟的功率谱在波频处与模型试验结果吻合良好，但是对于低频处的响应能量有所低估.图9给出了数值模拟与模型试验的纵荡响应对比.图中：ζmean为响应的平均值；ζmax为响应的最大值；ζSTD为响应的标准差.可以看出，风力机的纵荡的试验平均值为10.9 m，试验最大值为16.1 m，数值模拟与试验结果偏差为11.8%，试验值较数值模拟值稍大，但是数值模拟与试验值的平均值、最大值以及标准差相差的趋势是一致的，可以看出，试验与数值模拟吻合良好.

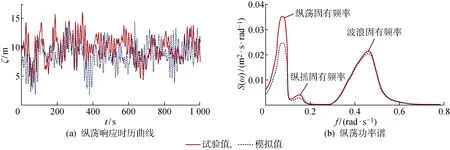
图8 浮式风力机极限海况下的纵荡响应时历曲线及纵荡功率谱Fig.8 Surge time history curves and surge spectrums for extreme condition of FOWT

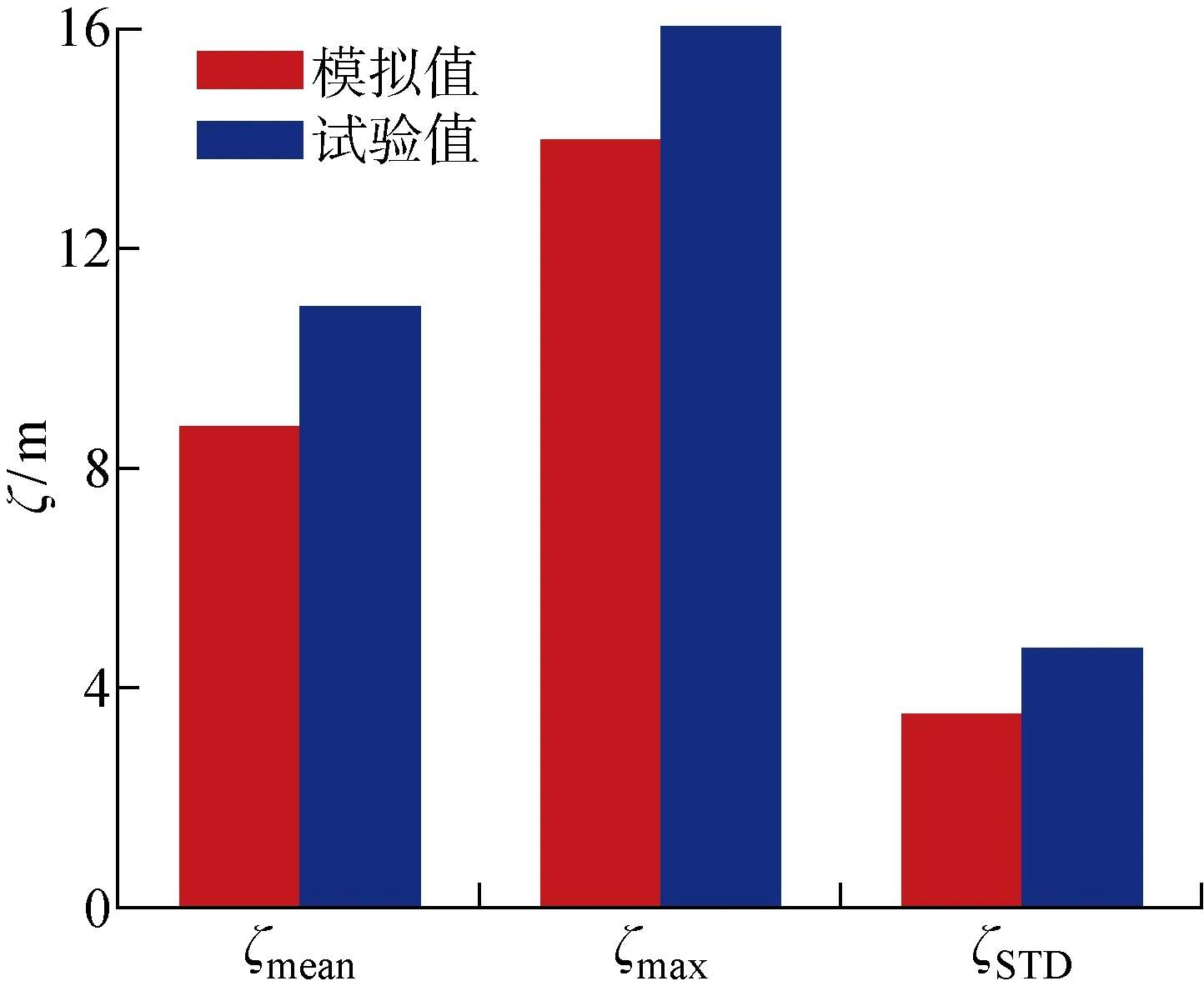
图9 极限海况下纵荡响应数值模拟与试验值对比Fig.9 Comparison of surge response between simulation and test results under extreme condition

3.2 纵摇运动

图10所示为纵摇响应时历曲线以及纵摇功率谱模型试验和数值模拟的结果.图10(b)表明，对于纵摇运动，存在3个能量峰值点，分别对应风力机的纵荡固有周期、纵摇固有周期以及波浪周期.风力机纵摇功率谱在纵荡的固有周期处出现峰值，这也验证了图8(b)中纵荡和纵摇存在一定的耦合作用.纵摇功率谱在纵摇固有周期处出现最大的能量峰值，这说明在极限海况下，纵摇运动的能量主要集中在低频运动.纵摇功率谱在波浪的周期处同样出现了较明显的峰值，说明了波浪载荷对风力机纵摇运动影响较大.图11给出了纵摇响应数值模拟与模型试验的对比.可以看出，风力机纵摇的试验平均值为2.2°，这说明在极限海况下，Spar型基础满足风力机的稳性保障要求.风力机纵摇的试验最大值为9.2°，极限海况下的最大纵摇角不超过 10°，符合Spar型浮式风力机的设计标准[16].风力机最大纵摇值的数值模拟与试验结果偏差为11%，纵摇动动响应的数值模拟与试验值吻合良好.

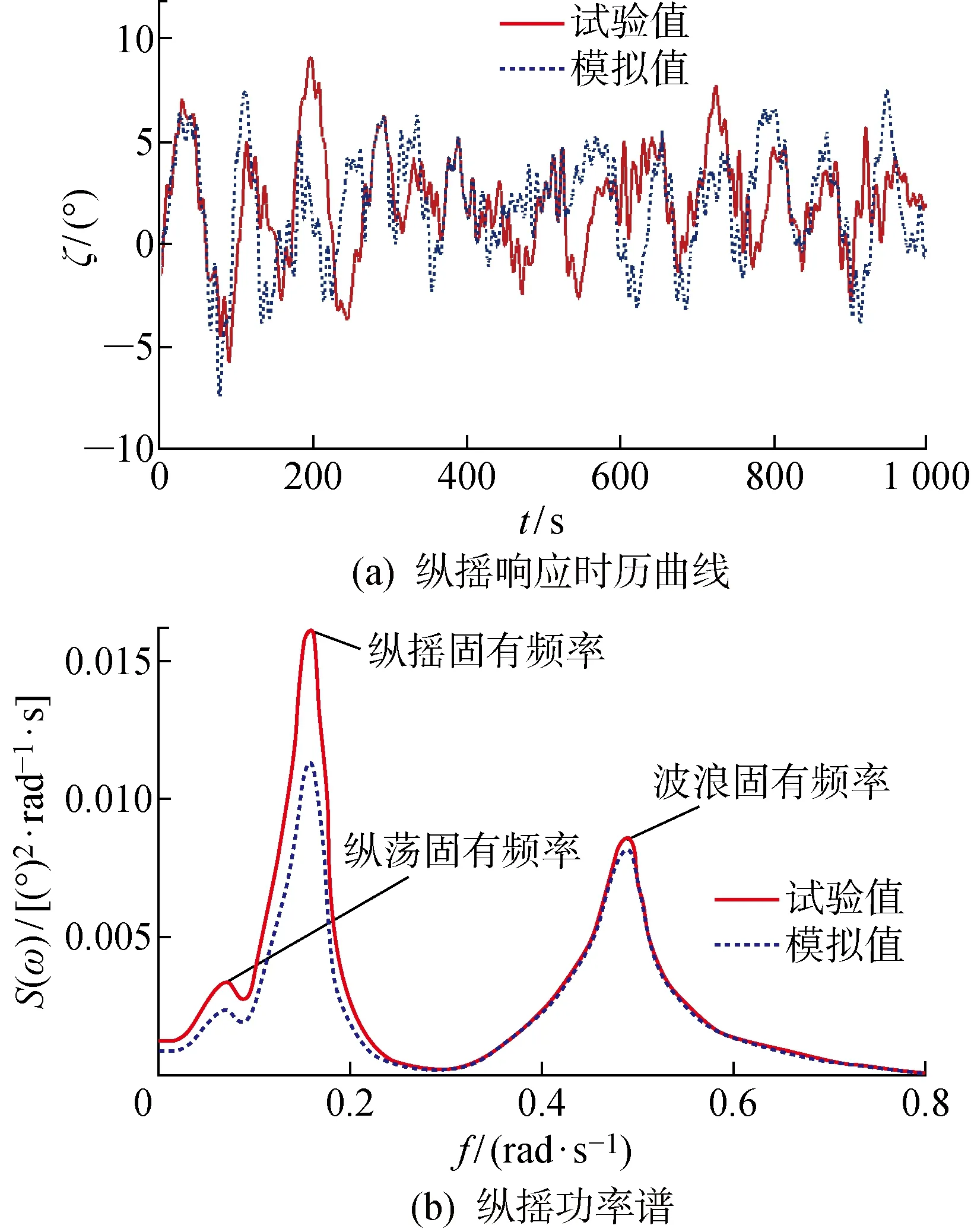
图10 浮式风力机极限海况下的纵摇响应时历曲线及纵摇功率谱Fig.10 Pitch time history curves and pitch spectrums for extreme condition of FOWT

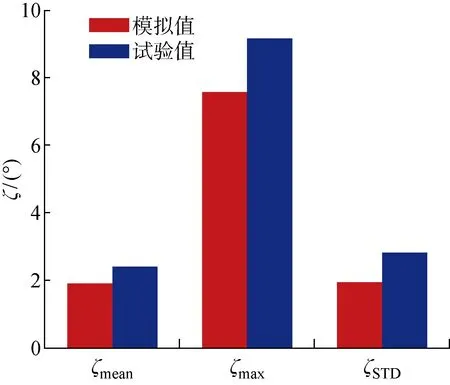
图11 极限海况下纵摇响应数值模拟与试验值对比图Fig.11 Comparison of pitch response between simulation values and test results under extreme condition

3.3 垂荡运动

由数值模拟和模型试验得到的垂荡响应时历曲线以及垂荡功率谱如图12所示.图12(b)表明，对于垂荡运动，存在2个能量峰值点，分别对应风力机的垂荡固有周期以及波浪周期.垂荡功率谱在波浪的周期处出现了最大的峰值点，这说明了波浪载荷是风力机垂荡运动主要影响因素.图13给出了垂荡响应数值模拟与模型试验的对比.可以看出，在极限海况下，风力机垂荡平均值基本处于平衡位置，垂荡的试验最大值为2.2 m，不足风力机整体高度的1%，说明风力机的Spar基础能够保障风力机在极限海况下垂荡响应处于安全范围.风力机最大垂荡值的数值模拟与试验结果偏差为9%，垂荡运动响应的数值模拟与试验结果吻合良好.

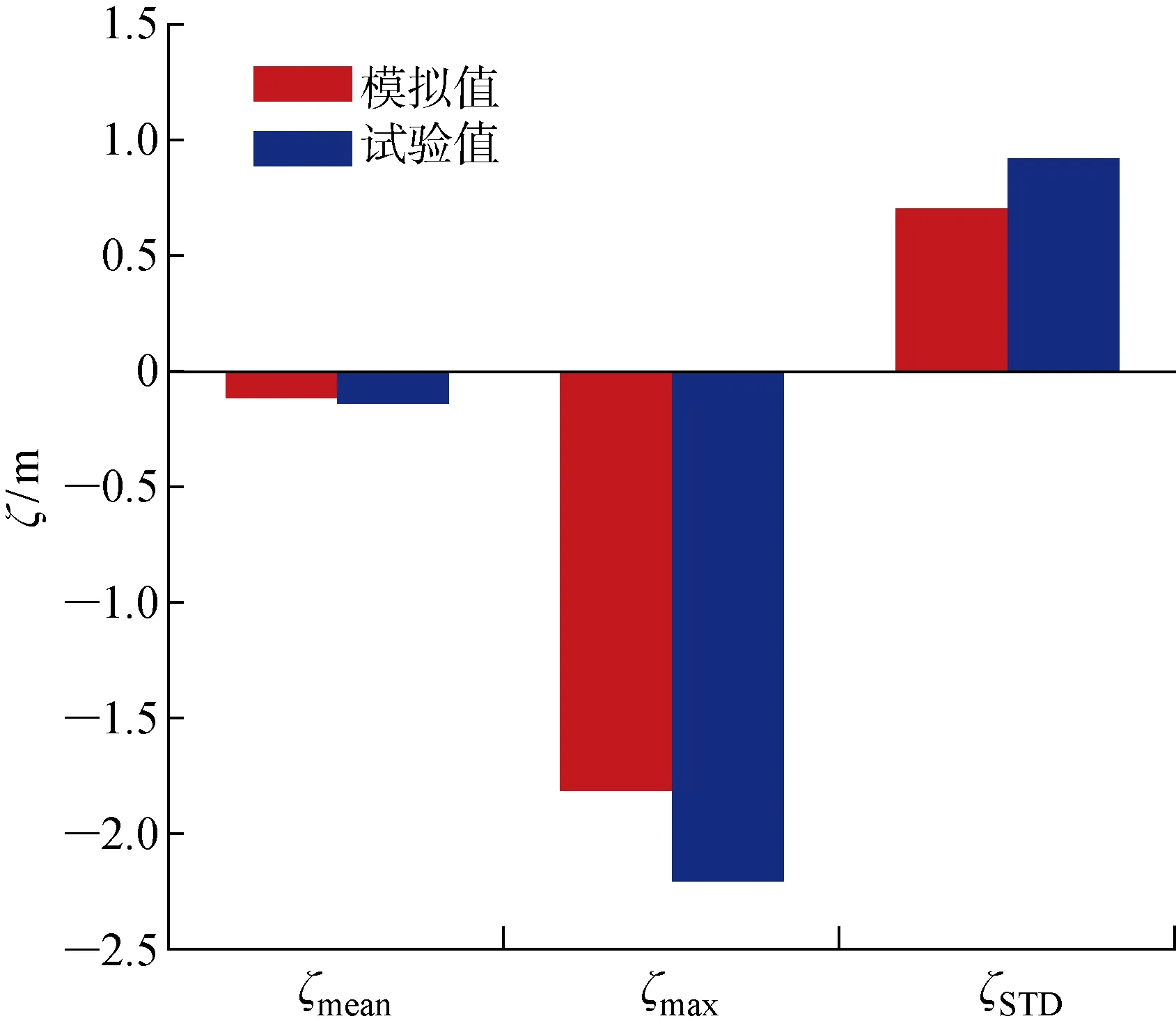
图13 极限海况下垂荡响应数值模拟与试验值对比Fig.13 Comparison of heave response between simulation values and test results under extreme condition

3.4 导缆孔处锚链的受力情况

图14所示为导缆孔处锚链受力的时历曲线以及锚链受力功率谱数值模拟和模型试验的结果，图中Ft为导缆孔处锚链受力.图14(b)表明，对于锚链受力，存在3个能量峰值点，分别对应风力机的纵荡、垂荡固有周期以及波浪周期.浮式风力机在风力机的纵荡、垂荡固有周期处存在峰值，说明了锚链受力与风力机的运动存在耦合现象，这也可以从本文2.3节中锚链力的计算理论中得到验证.锚链受力功率谱在波浪的周期处出现了最大的峰值，这说明了波浪载荷是锚链受力的主要影响因素.图15给出了锚链受力数值模拟与模型试验的对比.图中：Fmean为锚链受力的平均值，Fmax为锚链受力的最大值，FSTD为锚链受力的标准差.可以看出，在极限海况下，导缆孔处锚链受力最大值约为平均值的2倍，最大值为 2 380 kN，远小于表1中的锚链破坏力 11 981 kN，这说明锚链可以保障风力机在极限海况下安全.

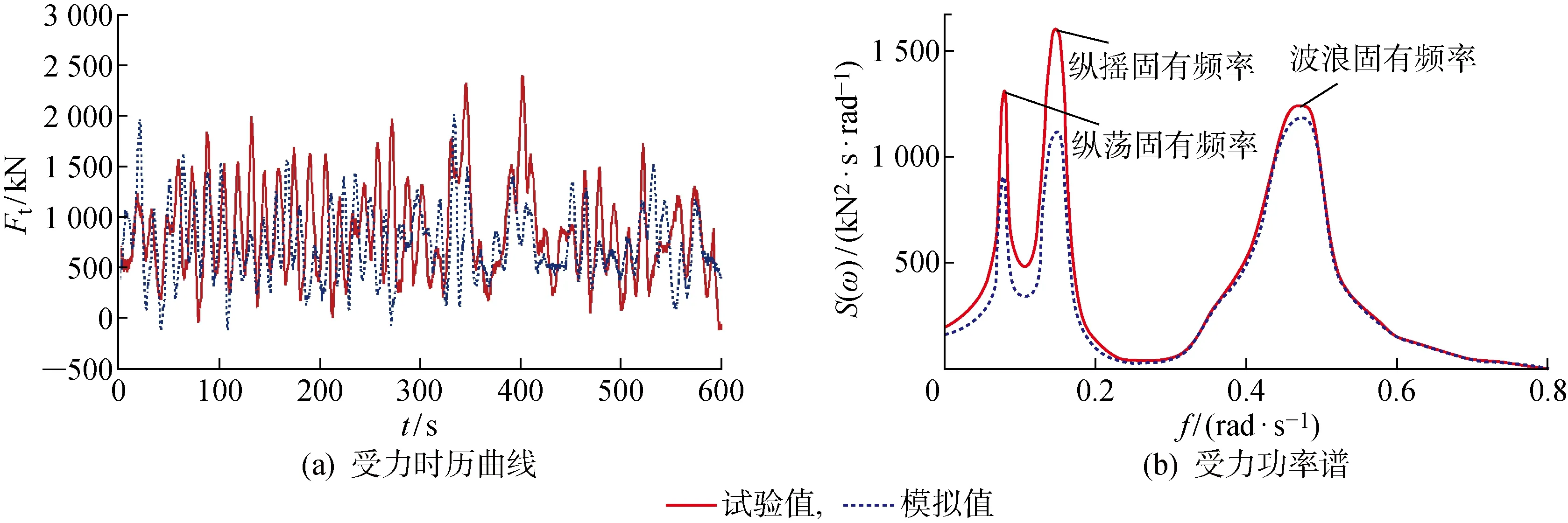
图14 浮式风力机极限海况下的锚链受力时历曲线及锚链受力功率谱Fig.14 Fairlead force time history curves and fairlead force spectrums for extreme condition of FOWT

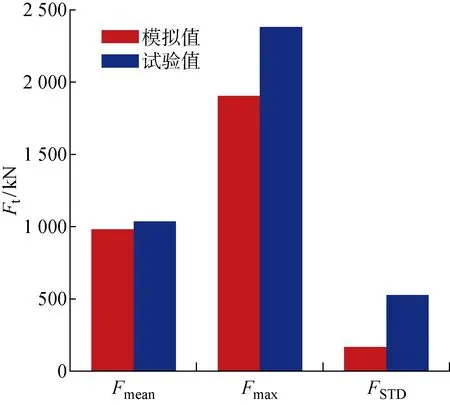
图15 极限海况下锚链受力数值模拟与试验值对比Fig.15 Comparison of fairlead force between simulation values and test results under extreme condition

从纵荡、纵摇、垂荡以及锚链力的试验与数值计算结果的比较可以看出，运动特性趋势都是一致的，但是相对于数值模拟的计算值，试验值稍大.数值模拟和模型试验结果差异的主要原因有以下两点：

(1) 模型试验中，风力机的六自由度运动响应是通过测量安装在塔筒上的测量灯球的位置来获得的，试验的塔筒具有一定的柔性，会产生弹性变形.数值模拟中，塔筒假定为刚体，不会变形；

(2) 数值模拟时没有考虑二阶差频波浪力作用，导致数值模拟对纵荡和纵摇固有周期处的响应能量有所低估.在后续计算优化中，可以对二阶差频波浪力产生的低频运动进行补充计算，从而进一步提高数值模拟的准确性.

3.5 极限状态分析

极限海况对于浮式风力机的生存状况至关重要，极限海况下的极限载荷是分析风力机在极限状态下结构强度的重要数据，表征了结构抵抗极端载荷的能力.浮式风力机属于细长体结构，受力后产生的形变主要为弯曲形变，局部载荷参数(如危险截面处的剪力、弯矩大小)对总体结构强度影响很大.按照规范要求和载荷评估结果，风力机机舱和塔筒连接处最有可能产生受力极限状态.为了确定风力机的最危险状态，总结了5个关键载荷参数作为判断极限状态的依据，并对极限海况下风力机机舱和塔筒连接处受力情况进行了试验测量.风轮系统受力测量点与坐标系如图16所示.风力机的主要受力极限状态有：

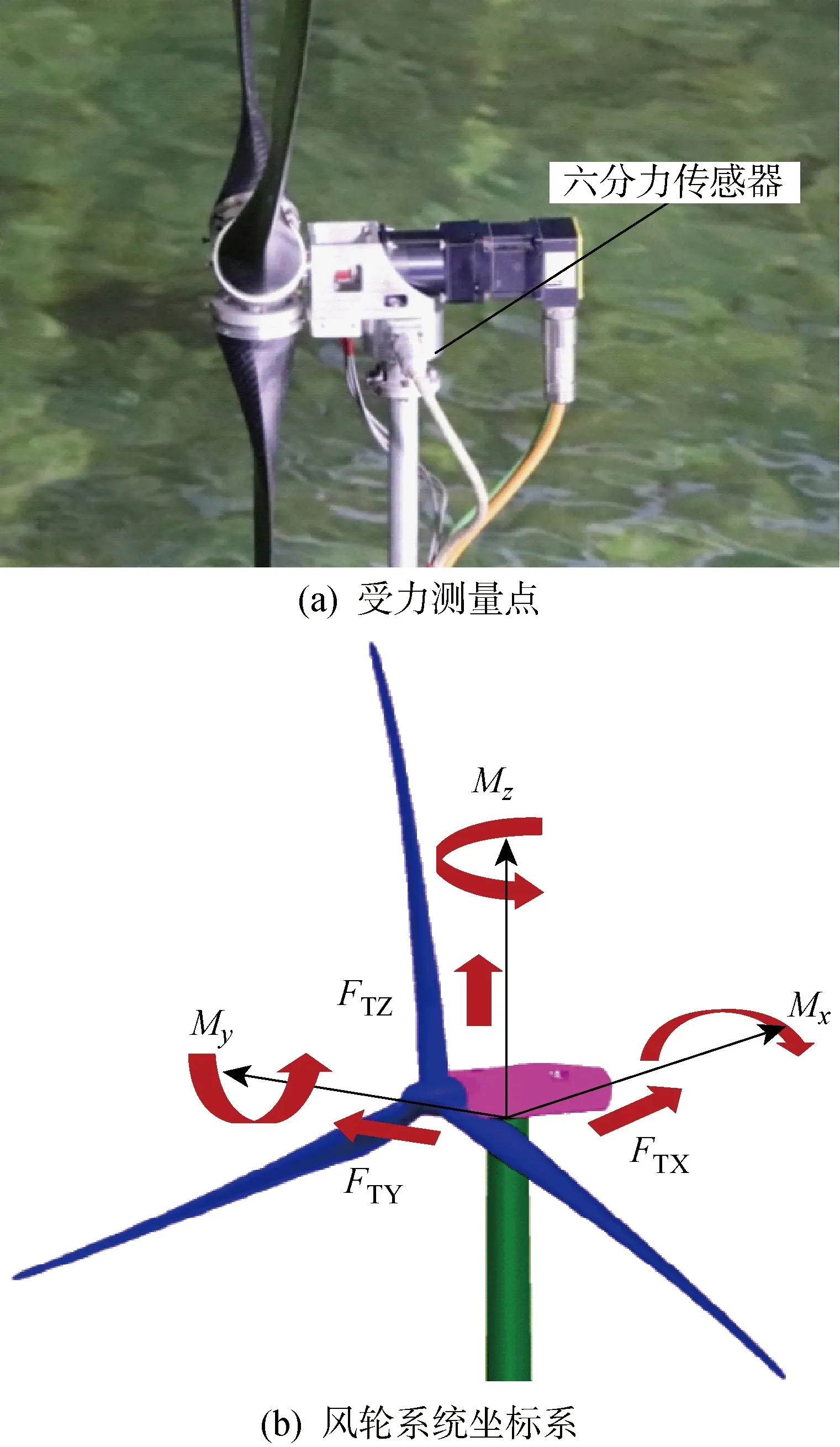
图16 风轮系统受力测量点与坐标系Fig.16 Force measuring point and coordinate system of FOWT rotor system

(1) 轮毂处横向推力最大状态Fmax；

(4) 机舱和塔架连接处扭矩最大状态MZmax；

(5) 风力机最大纵倾角状态Pmax.

通过对关键位置的载荷进行测量和数值模拟，得到了极限海况下风力机的极限载荷，具体数据由表5给出，表中F为横向推力，FT为顶部剪力，M为顶部弯矩，MZ为顶部转矩，P为纵倾角.表5的对角线为相应载荷分量的最大值，同时也给出了相应时刻其他载荷分量的结果，如表5所示，风力机横向推力最大值和塔筒顶部剪力最大值对应着比较大的纵倾角，但是推力最大值、顶部剪力最大值并不发生在纵倾角最大的时刻.这是由于风力机除了发生纵摇运动之外，还会有较小的横摇运动，会对塔筒顶部产生较小的横向剪力，所以塔筒顶部总的剪力最大值实际发生在风力机纵摇和横摇综合都比较大的时刻.风力机顶部弯矩最大值和顶部扭矩最大值则是发生在纵倾角接近于0°的时刻.以上结论表明在对风力机进行危险状态分析时，不能单考虑风力机运动响应最大的时刻，需要综合考虑风力机多个危险状态.

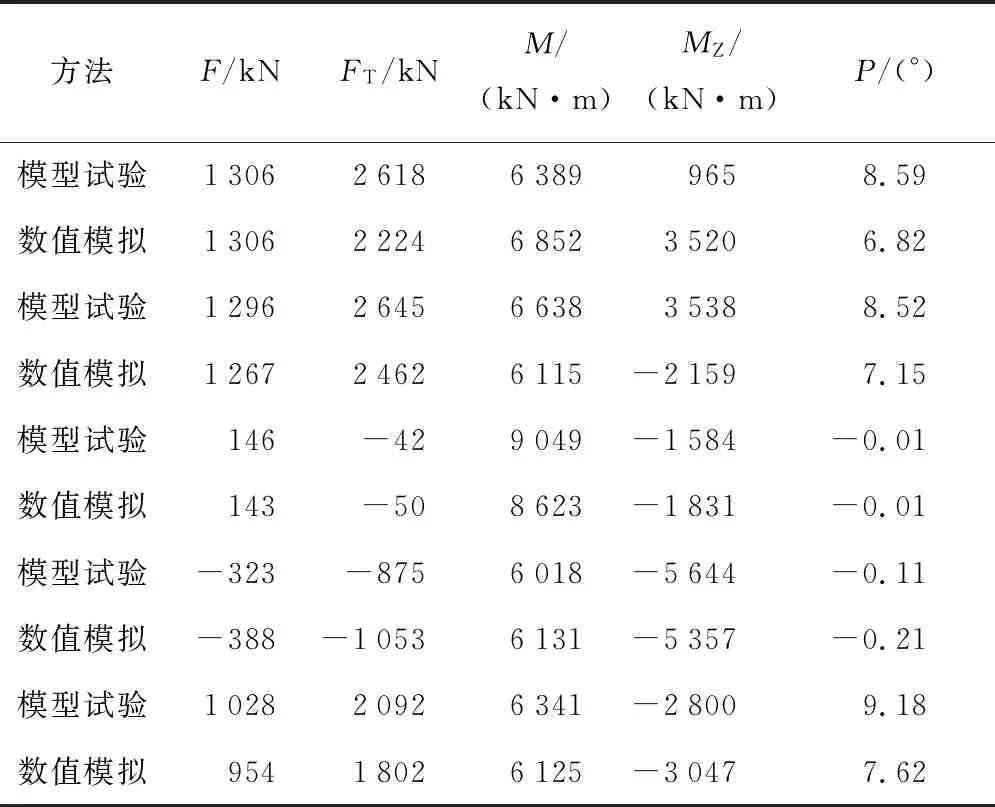
表5 极限海况下风力机极限载荷表Tab.5 Ultimate load of FOWT under extreme condition

从表5还可以看出，试验得出的受力情况与数值模拟的结果相近，但是试验结果总体较大，为了保证结构的安全，在结构强度计算时，应该选择试验参数进行后续结构分析.通过表5对风力机的载荷极限状态进行预报，为进行结构强度计算提供了必要的理论依据和计算参数.

4 结论

以新型6 MW Spar型浮式风力机为研究对象，在极限海况下对风力机进行了模型试验，得到了风力机的运动响应、锚泊系统受力以及风力机危险受力点(机舱和塔筒连接处)的受力情况.采用数值仿真软件FAST对风力机在极限海况下的六自由度运动特性及系泊系统响应特性进行了全耦合分析，验证了数值仿真模型的可靠性.通过对浮式风力机的数值模拟结果和模型试验结果进行时域、频域和统计分析对比，得出如下结论：

(1) 数值模拟与模型试验结果整体吻合良好，较好反映了风力机各自由度运动之间的耦合情况.在极限海况条件下，Spar型浮式风力机的纵荡运动和纵摇运动存在一定的耦合作用，垂荡运动与纵荡运动和纵摇运动耦合不明显.对于纵荡运功响应，能量主要集中在纵荡固有频率和波浪频率处；对于纵摇运动，能量则主要集中在纵摇固有频率和波浪频率处.除此之外，导缆孔处锚链的受力与纵荡运动和纵摇运动存在明显的耦合现象.

(2) 模型试验与数值模拟的结果趋势一致，模型试验的结果偏大，偏差的主要来源于数值模拟中对二阶差频波浪力的忽视和模型试验中塔筒的弹性变形.虽然数值模拟与试验结果有一定的偏差，但是两者的趋势是一致，偏差处于可接受范围，运用FAST软件进行浮式风力机数值模拟分析具有一定的可靠性.

(3) 对浮式风力机进行了极限海况下的水池模型试验，分析了风力机危险受力点的极限受力状态，结果表明：在对风力机进行危险状态分析时，不能单考虑风力机运动响应最大的时刻，需要对风力机多个危险状态综合考虑，风力机受力最危险的状态一般发生在运动平衡位置和运动幅值最大处.通过数据分析，对风力机的载荷极限状态进行了预报，为结构强度计算提供了必要的理论依据和计算参数.