粗糙底床对持续入流式异重流掺混和湍流特性的影响
韩东睿,余俊杨,袁野平,贺治国,王雨杭,林颖典
(浙江大学 海洋学院,浙江 舟山 316021)
异重流,又称密度流或者浮力流,其是在重力场作用下,两种流体密度的差异造成水平压力梯度,从而产生相对运动的现象[1].在自然环境和实际工程中,异重流现象广泛存在,在雷诺数极大或者极小的情况下,都会形成典型异重流,如火山岩浆、气流锋.所以其是不同专业领域,如流体力学、地质学、海洋学、环境工程学、河口学等研究的热点[2].
野外观测异重流具有很大的不确定性,也需要投入大量人力及物力[3],故实验室水槽试验成为各领域学者探索异重流的主要方法之一.异重流按出流方式不同分为两类:开闸式异重流和持续入流式异重流[4].相对于开闸式异重流,持续入流式异重流更加符合大部分实际工况,但是前人对其研究程度远不如开闸式异重流[5].过去大多数异重流水槽试验都是基于光滑底床,如Middleton[6]、Britter等[7]、Chowdhury等[8].现实中,粗糙底床是影响异重流运动机制的重要环境因素之一[3].近几年,也有少部分国外学者对粗糙底床的影响机制展开研究.如Peters等[9]结合激光诱发荧光技术(LIF)对异重流流经粗糙底床时头部区域的动力特征进行分析;La Rocca等[10]聚焦三维异重流,其发现随着底床粗糙度增加,异重流头部速度逐渐衰减,并得到粗糙度的存在会提前异重流从滑塌阶段到自相似阶段转变的结论;Özgökmen等[11]通过对粗糙底床异重流的数值模拟研究,指出粗糙底床增强了摩阻力,间接影响异重流的速度场和密度场;Adduce等[12]选用石英砂来模拟粗糙底床,结合图像处理技术验证了Özgökmen等[11]的结果;Nogueira等[13]则对开闸式异重流流经光滑与粗糙底床的试验结果进行对比分析;Varjavand等[14]综合分析了在粗糙底床影响下,成分驱动型异重流和颗粒驱动型异重流典型速度剖面及密度剖面的变化,并发现了粗糙底床中的局部区域峰值点的“爬升”现象;Ozan等[15]和Zhou等[16]结合大涡模拟来研究异重流流经交错分布独立障碍物(非连续的粗糙底床)时的动力学特性,其发现随着障碍物密度的增加,流态从贯穿流向跃升流的转变会引起异重流头部的加速;Cenedese等[17]发现粗糙底床单元的密度和高度会影响异重流形态和掺混过程;Asghari等[18]研究了不同的粗糙底床形态对异重流作用的机理;Kashefipour等[19]提出了粗糙度对异重流典型垂向速度剖面影响的经验公式,结合前人的结果,证明其较有具有较好的适用性;林颖典等[20]结合粒子图像测速(PIV)技术对异重流流经粗糙底床的速度场和涡度场进行了分析等等.
综上所述,目前关于粗糙底床对异重流影响机制研究的试验,其考虑到试验水槽简易性而多采用开闸式出流,而现实工况中异重流侵袭的时间都较长,持续入流出流方式更具有实际参考价值.由于驱动浮力的差异,两种不同出流方式的异重流在头部速度、挟带掺混等宏观方面皆体现出不同,并且用不同方法去推求和对比近底床区域的剪应力水平,可以作为评价异重流侵袭和泥沙沉积程度的指标.此外,基于粗糙底床的异重流湍流结构的研究有待完善.
因此,本文利用水槽试验手段,选用持续入流出流方式,综合考虑异重流初始质量分数和底床粗糙度两个变量,对成分驱动型异重流扩散特性和湍流特性等进行研究.试验利用高速摄像机并结合自编MATLAB程序分析异重流头部位置、头部速度、掺混系数等扩散特性;运用声学多普勒流速仪(ADV) 测量异重流瞬时三维速度,分析不同断面的湍流强度、雷诺应力等湍流特性,对比雷诺应力法和湍动能法计算底床剪切力.本文结果可为实际工程中流经粗糙底床的异重流运动特性研究提供科学依据.
1 试验设置
1.1 试验装置及步骤
持续入流式异重流装置水槽分为试验槽(330 cm×25 cm×30 cm)和出流槽(30 cm×25 cm×30 cm)两部分,所有工况闸门开启高度h固定为10 cm,水槽系统外接恒定入流装置,通过泵管系统实现持续入流.试验槽下游和出流槽后设有等高溢流堰,保证试验过程中水位恒定,如图1所示.试验采用不同粒径鹅卵石模拟粗糙底床,其粗糙程度用D50[13](累计粒度分布百分数达到50%时所对应的粒径)表征.选用鹅卵石模拟粗糙底床原因如下:① 保证能够使用ADV测量近底床区域流速;② 通过粒径改变来实现粗糙度改变;③ 沿主流方向异重流发展过程可以完整观测分析.整个水槽系统中均铺设粗糙底床,从而消除底床抬高对入流水头的影响.选取试验槽中两个特征断面(距离闸门1.1 m处为断面1,距离闸门2.2 m处为断面2),每个特征断面中心线上设取7个特征点(分别距离底床0.5,1,1.5,2,3,5,10 cm).试验中重流体为成分驱动盐水异重流,选用食用色素对其染色.闸门开启后,盐水从出流槽射流进入环境流体中,沿着水槽底部向前运动,盐水和环境水体形成典型对流运动[16],当异重流到达试验槽末端(溢流堰)后试验结束.

图1 持续入流异重流试验水槽设置(mm)Fig.1 Setup of experimental flume for continuous-flux gravity current (mm)
实验室温度恒定为20 ℃,用高速数码相机(分辨率为 1 920像素×1 080 像素,帧率为25 帧/s)记录异重流二维行进过程、形态结构等.用ADV测得两个特征断面(共计14个特征点)的三维流速,即纵向瞬时速度u,横向瞬时速度v和垂向瞬时速度w.为了保证测量数据质量,应保证信噪比(SNR)在15以上[21].本试验数据采样频率为25 Hz,单次ADV试验数据采集时长均不少于60 s,且所有组况下的ADV数据均已降噪处理.
1.2 特征参数与工况设计
流体之间密度的差异导致浮力梯度的存在是产生异重流的根本原因[1],可用有效加速度进行描述,其定义为
(1)
式中:ρc为异重流密度;ρa为环境水体密度;g=9.81 m/s2为重力加速度.
无量纲的雷诺数为惯性力与黏滞力的比值,可表示流体的流态特征,此处定义的异重流头部雷诺数为[13]
(2)
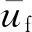
无量纲的弗劳德数为惯性力与重力的比值,此处定义的异重流头部密度弗劳德数为[14]
(3)
式中:uf为异重流头部瞬速度;hf为异重流头部瞬时高度.
无量纲的理查森数为浮力项与剪切项的比值,可表征异重流与环境流体的掺混特性,此处定义的异重流总体理查森数Rig和梯度理查森数Rig1分别为[14]
(4)
(5)
式中:ρ1为流体的局部密度值.

(6)
(7)
(8)
表1为持续入流式异重流试验工况及参数.盐水异重流初始质量分数为wini=1.75%,2.50%,3.25%;粗糙度取为D50=0,3,10,30 mm,其中D50=0组设为对照组(光滑底床).试验中各组雷诺数均大于 2 000,认为异重流流态为湍流,可以忽略黏滞力对其影响[13].此外,试验中各组弗劳德数均小于1,故试验工况条件下,异重流为缓流流动.

表1 试验工况及相关参数Tab.1 Test conditions and parameters
2 试验结果分析
2.1 形态分析
图2为不同粗糙度下持续入流式异重流的形态对比图.在光滑底床时(见图2(a)),持续入流式异重流最终演变为稳态流动,相对于开闸式异重流,持续入流式异重流最大不同为尾部区域对头部区域的源补充,并且观察到尾部区域的上边界层近乎水平,典型异重流的尾部区域速度比头部区域速度大20%~40%[5],从而造成异重流尾部区域高度低于头部区域高度.综合上述原因,相对于开闸式异重流,持续入流式异重流密度差异削减更慢,与周围流体掺混的范围更广,持续时间更长.

图2 不同粗糙度下持续入流式异重流掺混对比图Fig.2 Mixing and entrainment comparisons of continuous-flux gravity current at different bed roughnesses
图2(b)和2(c)为持续入流式异重流流经不同粗糙度底床(D50=3 mm、D50=30 mm)的发展过程,结合图2(d):相同初始质量分数的异重流流经相同位置时,其头部区域颜色随着粗糙度增加而逐渐淡化,各组试验盐水和染料配比恒定,同时进行了预备试验,已验证色素与盐水有较高相容性,因此异重流区域颜色改变可以充分反映应异重流密度的变化.异重流头部区域淡化现象明显高于尾部区域,验证了Britter等[7]关于异重流头部是动量交换和掺混挟带主要区域的结论.异重流质量分数减小会直接影响到与环境流体密度差异,从而驱动浮力减小致使其持续时间变短,侵袭范围变小.
2.2 头部位置
图3给出不同变量条件下异重流无量纲的头部速度.图3(a)为相同异重流初始质量分数工况,而图3(b)为相同粗糙度工况.在粗糙度相同情况下,异重流的速度与初始质量分数呈正相关:初始质量分数越高,异重流与环境流体之间密度梯度就越大,从而驱动浮力越大,异重流扩散速度越快;在初始质量分数相同情况下,异重流头部速度与底床粗糙度呈负相关:粗糙度存在会增加底床摩阻力,从而削减异重流水平速度.此外,近底床区域掺混加剧导致异重流驱动浮力减弱也是重要的影响因素.在高粗糙度(D50=30 mm)情况下,初始质量分数升高并没有显著提升异重流头部速度,原因在于:虽然升高异重流初始质量分数能获得更大驱动浮力,但高粗糙度底床的摩阻、掺混等抑制影响更甚.因此高粗糙度、高初始质量分数工况时,底床粗糙度是控制其运动特性的主要因素.

图3 不同变量条件下异重流无量纲的头部速度Fig.3 Dimensionless head velocity for gravity current under different variable conditions
图4为采用双对数坐标系的无量纲持续入流式异重流位移-时间图.Testik等[5]指出典型持续入流式异重流扩散发展分为3个阶段:第1阶段为浮力射流阶段;第2阶段为惯性阶段,此阶段惯性力-驱动浮力为主导控制力;第3阶段为黏性阶段,此阶段黏滞力-驱动浮力为主导控制力.图4(a)基于光滑底床,异重流扩散发展分为典型的射流阶段(斜率k≈2/3)和惯性阶段(斜率k≈1).当粗糙底床存在时,如图4(b)~4(d),异重流射流阶段受其影响很小,原因是射流阶段主要受上自由边界层控制,下固体边壁条件的改变不会显著影响该阶段.此外,随着粗糙度增加,图中惯性阶段的斜率k逐渐减小,在底床摩阻、掺混等机制影响下,异重流在惯性阶段不再维持恒定速度的状态.

图4 持续入流式异重流无量纲头部位置随时间变化关系Fig.4 Temporal evolution of dimensionaless current front position for continuous-flux gravity current
2.3 纵向时均流速垂向分布
典型异重流速度剖面以速度峰值点为界,分为壁面区和射流区[14].壁面区主要受异重流下固体边界控制,其为典型对数分布边界层;射流区主要受上自由边界控制,其为典型高斯剪切边界层.速度剖面表征如下.
壁面区:
(9)
射流区:
(10)
式中:um和hm为剖面速度峰值和峰值点距底床高度;u(z)和z为选取点速度和距底床高度;αv、βv和γv为经验系数.
图5为特征断面纵向时均流速uave沿水深分布图,以环境水深H为特征深度对距离底床高度z进行无量纲化.所有试验工况的密度弗劳德数均小于1(缓流),速度剖面均存在高于底床的峰值点,此与Sequeiros等[22]结论相吻合.速度峰值点的存在是异重流上自由边界和下固体边界协同作用的结果.随着底床粗糙度增加,速度峰值逐渐减小,峰值点逐渐从底床提升(除图5(a)的D50=30 mm工况),原因是粗糙底床强化下固体边界对异重流的控制,原上下边界协同的平衡被打破,速度峰值点提升后建立新的平衡.粗糙度存在会增加底床摩阻力,改变近底床区域的密度场,同时粗糙底床孔隙中的滞留环境流体会被异重流卷吸(详见2.6节),共同导致速度峰值减小.
图5(a)中D50=30 mm工况出现剖面速度峰值反常增大的现象(相对低粗糙度工况),究其原因:区别于明渠流,异重流有效加速度g′非常小,其宏观作用是迫使异重流于底床上运动,当其遇到障碍物(高粗糙度)时,会出现局部区域的加速,弱化底床的有效粗糙度,促使异重流通过该障碍物.此现象在Varjavand等[14]也被观察到,称为速度峰值点的“爬升现象”.图5(b)中“爬升现象”消失,说明异重流沿程扩散,粗糙底床对其控制加强,有效加速度g′造成的局部加速机制弱化至消失.

图5 持续入流式异重流特征断面纵向时均流速沿水深分布图Fig.5 Vertical distribution of mean velocity in longitudinal direction for continuous-flux gravity currents
2.4 湍流结构
异重流中湍流结构的形成归因于异重流与环境流体速度梯度变化造成的剪切不平衡[23].本试验利用ADV采集特征点三维流速,结合后处理软件WinADV过滤数据.本节综合考虑湍流强度(I)及雷诺应力等表征异重流的湍流特性.湍流强度定义为[24]
(11)
(12)
(13)

图6为持续入流异重流流经光滑底床和粗糙底床(D50=30 mm)的三维度湍流强度沿水深分布图.由图可知:对于光滑底床,纵向湍流强度远大于横向和垂向强度,其中垂向湍流强度稍强于横向湍流强度;对比于特征断面一(图6(a))、特征断面二(图6(b))发现:沿程异重流横向和垂向湍流强度变化不大,但纵向湍流强度值略有衰减,认为其是湍流能量耗散的缘故.由图6(c)和6(d)可知:粗糙底床上,纵向湍流强度仍是异重流湍流结构的主导,横向湍流强度相对于光滑底床有轻微增加,但是异重流壁面区和射流区的垂向湍流强度增加幅度明显:垂向湍流强度直接反映异重流与环境流体的掺混水平.壁面区湍流强度增加是由于粗糙底床孔隙中的滞留环境流体会被异重流卷吸造成的,此外,粗糙底床附近会形成强化湍流边界层(相对于光滑底床),会间接影响到异重流上自由边界的剪切不稳定性,从而增加该区域的垂向湍流强度.底床粗糙度越大,该强化湍流边界层越厚,其对异重流上自由边界的剪切不平衡影响亦越大.由于沿程粗糙底床对异重流的控制逐步加强,所以相比于特征断面一(图6(c)),特征断面二(图6(d))中纵向湍流强度值略有增加.
此外,由图6也可发现:湍流强度极小值点出现在速度剖面峰值点附近.在速度剖面峰值点附近,∂u/∂x≈0,此处为湍流强度最弱区域,此区域为受掺混机制影响最小的区域,可称为“最慢稀释区域”.所有工况条件下湍流强度极小值均大于0,表示该区域是上自由边界控制的射流区和下固体边界控制的壁面区之间动量和质量交换的重要通道.
此外,以湍流强度极小值点为界,上区(射流区)和下区(壁面区)各存在一湍流强度极大值点,表征两区域存在较大剪切(∂u/∂x)不稳定性.对于光滑底床,下区湍流结构主要受下固体边界摩阻和“鼻子”效应影响,上区湍流结构主要由上自由边界环境流体与异重流间剪切不稳定性(掺混)控制.对于粗糙底床,额外的底床掺混对下区湍流结构的影响不可忽略.此外,近粗糙底床区域的附加湍流边界层会强化上区环境流体与异重流间剪切(掺混)不稳定性.
研究异重流湍流结构特性,必须考虑脉动流速对时均流速的影响.湍流水团的交换在流层之间产生剪应力,实质就是流速分布不均匀而发生动量交换,从而产生雷诺应力[24].试验基于ADV采集大量流速数据,滤过处理后对雷诺应力进行分析.对于二维不可压缩牛顿流体雷诺应力[24]表达为
(14)
(15)
(16)
式中:ρ表示异重流密度,取为 1 016.6 kg/m3;τxx、τzz分别表示纵向和垂向雷诺正应力;τzx表示作用于法向量为z轴的平面沿x轴方向的雷诺切应力.
对比湍流强度表达式(式(11)~(13)),τxx、τzz表征的异重流纵向和垂向雷诺正应力沿水深分布规律应与Iu、Iv一致,在此不再赘述.


图7 异重流特征断面雷诺切应力沿水深分布Fig.7 Vertical distribution of Reynolds shear stress at characteristic sections for gravity current
2.5 底床剪切力
估计水流与壁面间的切应力在泥沙输移和水利工程安全方面意义重大[24-25].本节依据国内外学者对水流和壁面间切应力估计方法,对持续入流式异重流对光滑底床和粗糙底床的剪切力进行评估.
在异重流下固体边界附近,取该点雷诺应力值为水流对固体边界的剪应力[26],即雷诺应力法,简称为RS法,定义底床剪应力为
(17)
式中:U*为底床摩阻速度.

(18)
此时,结合式(17)和式(18)得到:
Kim等[28]提出底床剪应力与湍流动能(TKE)之间的经验公式,即湍动能法,简称为TKE法,具体表达如下:
(19)
式中:C1为经验系数,其值一般取为0.19.
表2为根据RS法和TKE法计算的持续入流式异重流对底床剪应力值.由表中数据可得,利用TKE法求得的底床剪应力均小于同粗糙度下的RS法.沿程湍流结构逐步建立,所以特征断面2中两种方法的相对误差更小.由于仪器测量受限,两种方法均采用底床上方0.5 cm处湍流数据.此外,TKE法中C1的取值是否符合该工况有待商榷,故由RS法计算的底床剪应力更可信.

表2 重流对底床剪应力Tab.2 Bed shear stress applied by gravity current
2.6 掺混系数
光滑底床上,异重流扩散过程中与环境流体的掺混机制主要来表现在两个方面:一是上自由边界因为剪切不稳定性易形成开尔文·赫姆霍兹涡,简称为K-H涡,其是掺混机制的主要表现形式;另一方面,由于底床的无滑移边界条件,异重流头部区域形成“鼻子”结构,其下方环境流体会被卷吸进异重流头部区域[7].
Jacobson等[29]考虑二维侧面积变化定义异重流平均掺混速率we,表达式如下:
(20)
式中:A为持续入流式异重流的二维侧面积.
Morton等[30]假设掺混速率与头部速度呈正比,定义E为掺混系数,表征为
(21)
Turner[31]发现异重流掺混速率和Rig呈负相关.基于光滑底床,当Rig小于0.25时,掺混现象明显,当Rig大于0.8时,掺混作用被异重流密度梯度抑制,即交界面K-H涡弱化或消失.
图8为持续入流式异重流流经光滑底床的头部位置-掺混系数关系图.由图可知:异重流初始质量分数越大,初始掺混系数峰值越大.随着异重流扩散发展,掺混系数逐渐减小并最终稳定在较低水平.究其原因:异重流与环境流体密度差决定驱动浮力,由于持续入流存在尾部区域对头部区域的源补充,致使头部区域密度梯度(∂ρ1/∂z)维持在较高水平,故Rig1较大,掺混作用被抑制.对比之前的开闸式异重流试验[20],持续入流式异重流的掺混强度要小得多.

图8 光滑底床异重流头部位置-掺混系数关系图Fig.8 Head position versus entrainment coefficient for gravity current over smooth bed
图9为相同初始质量分数情况下的持续入流式异重流头部总体理查森数-掺混系数关系图,理查森数利用式(3)和(4)计算得出.由图可知:在理查森数相同情况下,异重流的掺混系数与粗糙度呈正相关.粗糙底床对异重流掺混的影响分为促进和抑制两个方面.抑制机制为:粗糙底床会加强底床摩阻,降低异重流整体速度,从而增大梯度理查森数,致使掺混作用被弱化.促进机制为:粗糙度存在会强化近床区域的湍流边界层,高粗糙度情况下,该附加湍流边界层甚至可以影响到上自由边界层,从而强化剪切不平衡.此外,粗糙度增加致使底床孔隙率增大,滞留环境流体被异重流覆盖卷吸.由此,基于粗糙底床的异重流掺混系数主要受两个因素影响,即

图9 异重流总体理查森数-掺混系数关系图Fig.9 Rig versus entrainment coefficient for gravity current
E=f(Rig,D50)
(22)
3 结论
(1) 基于粗糙底床,持续入流异重流惯性阶段出现减速趋势.异重流头部速度与底床粗糙度呈负相关,与初始质量分数呈正相关.在高粗糙度及高初始质量分数的工况,底床粗糙度是控制异重流运动特性的主要因素.
(2) 持续入流异重流纵向时均流速速度剖面存在高于底床的峰值点.随着底床粗糙度增加,速度峰值逐渐减小,峰值点逐渐提升.但当粗糙度增加到一定程度,异重流会出现局部区域加速,促进异重流通过粗糙底床,称为“爬升现象”.
(3) 对于光滑底床,纵向湍流强度远大于横向和垂向强度;对于粗糙底床,纵向湍流强度仍是其湍流结构的主导,垂向湍流强度增加幅度明显.
(4) 靠近底床附近,雷诺切应力为正值;远离底床区域,雷诺切应力为负值.随着距离底床距离增大,雷诺切应力在异重流中先减小后增大,在环境流体中逐渐减小.光滑底床上雷诺切应力相对于粗糙底床小得多.利用湍流动能法计算的底床剪应力均小于同粗糙度下的雷诺应力法.综合考虑,认为雷诺应力法求得的底床剪应力更可信.
(5) 光滑底床上,持续入流式异重流掺混系数随着其扩散逐渐减小并最终稳定在较低水平;在总体理查森数相同情况下,异重流掺混系数与底床粗糙度呈正相关.
本文采用盐水异重流进行持续入流水槽试验,后续会进一步考虑颗粒驱动的泥沙异重流,在泥沙自身的沉降作用的基础上,进行进一步探索,使试验结果更符合水库泥沙异重流的实际情况.

