基于神经网络的层状周期结构能量传输谱预测
刘陈续,于桂兰
(北京交通大学 土木建筑工程学院,北京 100044)
周期结构是指多个相同的基本单元在空间上周期性分布组合而成的结构,如周期分布的桩基础、多跨连续梁桥和高层建筑等.周期结构的特性使其能够产生相对于弹性波而言的频率衰减域,即在频率衰减域范围内的弹性波在通过周期结构时会被抑制或禁止,该特性产生的机理主要有两种:布拉格散射[1]和局域共振[2].
周期结构的研究与设计要求研究人员具备丰富的经验和理论知识,且对计算设备的要求较高.神经网络是实现人工智能(AI)的一种重要技术,如今神经网络的发展如火如荼,渐渐发展形成了一个新的分支——深度学习[3],在情感分析、自动驾驶和语音识别等领域发挥着重要的作用[4-7].近年来,在对应于光波和电磁波的光子晶体和超材料领域,用神经网络进行预测和设计的研究已经取得了一定的成果.文献[8]用多层感知器和极限学习机预测了光子晶体的能带曲线.Liu等[9]采用一种深度学习模型实现了光子晶体的反向设计.Ma等[10]提出了一种半监督学习的神经网络模型,能够依据设计要求直接输出超材料的拓扑结构.而对于弹性波(声波)却鲜有文献涉及,Liu等[11]利用自动编码器实现了基于能带理论的层状周期结构的反向设计.
层状周期结构是一种一维周期结构,即在空间上结构沿一个方向呈周期性的变化,国内外学者对其做了大量研究.Xiang等[12]通过实验验证了层状周期结构对于环境振动的衰减效果.Shi等[13]将由混凝土层以及橡胶砖构成的地基基础等效成层状周期结构,并研究了该基础的隔振性能.Huang等[14]通过数值分析研究了层状周期结构对表面波的隔振效果.
计算周期结构能量传输谱的方法有解析法和数值法等,但这些方法较为复杂且计算时间较长.神经网络可以根据输入快速准确地给出相应的输出,使用神经网络预测周期结构的特性能够极大地便利周期结构的研究与设计.本文采用两种神经网络——深层反向传播(BP)神经网络和径向基函数(RBF)神经网络,实现对层状周期结构能量传输谱的预测.神经网络作为一种快速预测技术,能够很好地辅助周期结构的设计.同时,层状周期结构能量传输谱的预测成功也为二维和三维周期结构的分析和智能反向设计打下了基础.
1 问题描述
层状周期结构属于一维周期结构,其基本单元由多种材料层层叠合而成,可以作为波屏障和隔振基础[12-14].在剪切横(SH)波作用下,二组元层状周期结构能量传输谱的预测如图1所示.周期结构由m个基本单元构成,其在水平方向上无限延伸;SH波以倾角θ入射.其中:d为基本单元的厚度;dA和dB分别为一个基本单元内材料A和材料B的厚度.考虑小变形,假定材料为理想连续线弹性介质且阻尼为0.

图1 层状周期结构Fig.1 Layered periodic structure
对于层状周期结构,可采用传递矩阵法[15]求解其能量传输谱,推导过程如下:
当SH波斜入射到层状周期结构时,其波动方程可表示为
(1)
式中:u(y,z,t)为结构在x方向上的位移;G为材料的切变模量;ρ为材料的质量密度;t为时间.
当考虑时谐平面波时,可假设
u(y,z,t)=U(z)eikyy-iω t
(2)
式中:ω为角频率;ky为SH波在y方向上的波数,由Snell定理可得ky为常数.将式(2)代入式(1)可得第n个基本单元中材料A和材料B的位移和应力分别为
(3)
i=A,B
(4)
i=A,B
当i=A时,(n-1)d≤z≤(n-1)d+dA;当i=B时,(n-1)d+dA≤z≤na.
(5)

根据两种材料界面处的位移和应力连续条件即可得相邻基本单元间的传递矩阵T.对于含有m个基本单元的层状周期结构,位移和应力在两端边界处成立如下关系
(6)
其中Tm可以简记为
(7)
为了更好地反映衰减情况,定义能量传递系数为透射波与入射波能量比值的对数,即
(8)
式中:Pin为入射波能量;Pout为SH波经过m层周期结构后的透射波能量.
由式(3)~(8)可得到能量传递系数的表达式如下:
Γ=
(9)
若材料A为铝(GAl=28.7 GPa,ρAl=2 730 kg/m3),材料B为环氧树脂(Ge=1.59 GPa,ρe=1 180 kg/m3),一个基本单元中dA=0.5 m,dB=0.5 m,m=8,不同入射角度下的能量传输谱如图2所示.从图2中可以看出,SH波在通过层状周期结构时,其能量在某些频率范围内有明显的衰减.就前两个频率的衰减域而言,随着入射角度的增大,能量传输谱的衰减幅值逐渐减小,衰减域的中心频率略向高频移动.

图2 “铝-环氧树脂”层状周期结构能量传输谱随SH波入射角度的变化Fig.2 Variation of energy transmission spectrums of layered periodic structure of “aluminum-epoxy resin” with SH wave incident angles
由式(9)可以看出,层状周期结构的能量传输谱与其结构参数构成映射关系,即每一组结构参数可以唯一对应结构的能量传输谱.如果把结构参数当作“输入”,能量传输谱当作“输出”,则可以利用神经网络来智能处理“输入”与“输出”的关系.神经网络通过对数据的学习来调节自身的参数值,最终可以找到数据中输入与输出的关系来模拟一个特定的函数,并能够准确和快速地将输入映射到输出上,其计算速度可达毫秒量级.但是,在数据充足的情况下,如何选择一个合适的神经网络模型模拟一个特定的函数关系是十分重要的,这直接影响着神经网络的预测精度.
层状周期结构的能量传输谱变化较为复杂,简单的神经网络模拟很难满足高精度要求.所构建的深层BP神经网络很好地解决了这个问题,并与RBF神经网络进行了对比分析.
2 数据集与神经网络
2.1 数据集
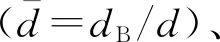
2.2 RBF神经网络
RBF神经网络有很好的泛化能力,具有模型简单、训练速度快等优点,如图3所示.RBF神经网络由一个输入层、一个隐含层和一个输出层组成,输入层到隐含层无权重连接,而隐含层到输出层有权重连接,神经元为径向基函数.RBF神经网络需要调节的参数有两类,一类是径向基函数的中心,另一类是隐含层到输出层的权重.
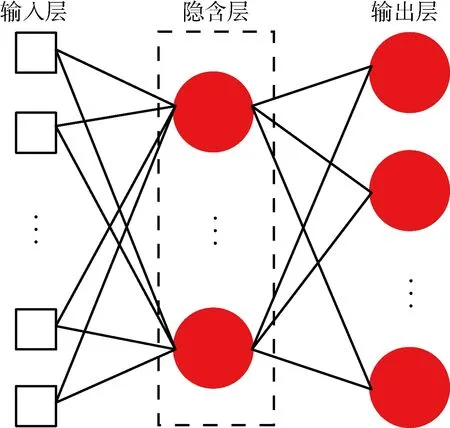
图3 RBF神经网络Fig.3 RBF neural network
RBF神经网络采用的径向基函数为多元二次函数,其表达式为
(10)
式中:x为一组输入值;c为径向基函数的中心;δ为形状参数.对于径向基函数中心点的计算,采用K-Means法,其表达式为
(11)
式中:S={S1,S2,…,Sk}为所有样布输入数据的集合,Si是S中的一个子集,由一个或多个样本输入数据组成;ci为Si中所有输入数据的均值.采用线性回归法计算RBF神经网络中的权重,其公式为
(12)
式中:β为权重;ytr为样本标签(即真实值);yNN为训练时RBF神经网络的输出值.
2.3 深层BP神经网络
与RBF神经网络不同,BP神经网络每层之间都由权重和偏差相连,并通过激活函数传递到下一层,其隐含层层数可以是多层的,如图4所示.在以往的文献中,大部分BP神经网络的隐含层一般不超过3层,导致其泛化能力不强.由于当时算法的限制,若隐含层层数较多,可能会出现梯度爆炸或者梯度消散的现象.而且当时的硬件水平较为落后,增加隐含层层数意味着需要调节的神经网络参数增多,一般的计算机很难承担起如此庞大的运算工作.如今神经网络技术飞速发展,计算机硬件性能日益更新,使得训练基于大数据的深层神经网络成为可能.
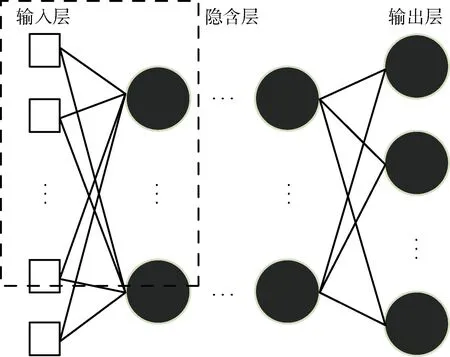
图4 深层BP神经网络Fig.4 Deep BP neural network
2.3.1激活函数 选取的激活函数有两种,一种是tanh函数,其能够使神经网络具有很好的非线性模拟能力;另一种是elu函数,其可以较好地缓解梯度消散的问题.其公式如下:
式中:p为预激活值;ε为可调参数.隐含层神经元采用的是tanh激活函数,输出层神经元采用的是elu激活函数.
2.3.2优化算法 经验性结果证明,Adam算法在实践中具有良好的性能,与其他随机优化算法相比具有较大的优势[17].因此,采用Adam算法优化梯度下降法,用于调节神经网络的参数,其公式如下:
(15)
φt=ι1φt-1+(1-ι1)gt
(16)
(17)
(18)
(19)
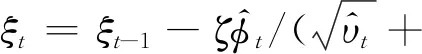
(20)

2.3.3代价函数 代价函数为均方差(MSE)函数的神经网络能够很好地估计有限样本的后验概率.对于深层BP神经网络,采用MSE作为其代价函数,其表达式为
(21)
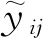
3 结果和讨论
分别利用深层BP神经网络和RBF神经网络预测层状周期结构的能量传输谱.考虑单参数、双参数和三参数变化的3种情况.单参数预测考虑填充比变化;双参数预测考虑切变模量比和密度比变化;三参数预测同时考虑填充比、切变模量比和密度比的变化.
对于预测精度的衡量标准,采用神经网络预测值与真实值(即标签)中每个点的平均绝对误差的绝对值,即
(22)

3种情况下训练深层BP神经网络时代价函数的收敛曲线如图5所示,其中Q为迭代次数.从图5中可以看出,3种情况下代价函数均收敛到了较小的值,由于对代价函数的数值取了对数,所以及其微小的变化也会使图中的收敛曲线显示出较大的振荡,这说明深层BP神经网络对于训练集的学习效果较好.
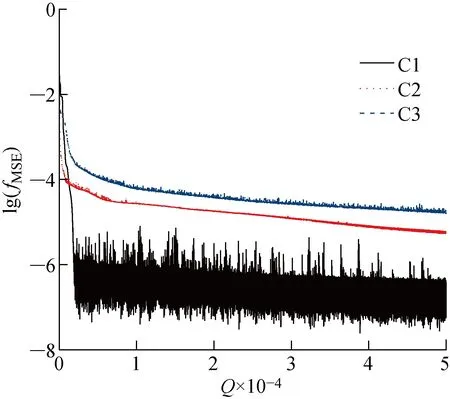
图5 3种情况下深层BP神经网络代价函数的收敛曲线Fig.5 Convergence curves of cost function for deep BP neural networks under three conditions
3.1 单参数变化
单参数变化时,数据集由训练集 I 和测试集 I 组成.RBF神经网络的结构为“1-15-100”,其中,“1”为输入层的维度,“15”为隐含层神经元的数目,“100”为输出层神经元的数目;深层BP神经网络的结构为“1-100-60-30-20-60-100”,其中,“1”为输入层的维度,最后一个“100”为输出层神经元的数目,其他数字表示相应隐含层神经元的数目.测试集Ⅰ中神经网络预测值与真实值(标签)的对比如图6所示.由图6可知,仅10组样本数据训练的深层BP神经网络和RBF神经网络获得了较满意的预测结果,两种神经网络的预测值与真实值的吻合度较高且精度相近.RBF神经网络的预测误差分别为0.39、0.48和0.58;深层BP神经网络的预测误差分别为0.36、0.47和0.59.两种神经网络预测一组数据所需时间约为2 ms.

图6 能量传输谱预测值与真实值对比(3个测试样本) Fig.6 Comparison of predicted values of energy transmission spectrum with real values (3 test samples)
3.2 双参数变化
双参数变化时,数据集由训练集 II 和测试集 II 组成.RBF神经网络的结构为“2-100-100”;深层BP神经网络为“2-100-60-30-20-60-100”.测试集 II 中4组神经网络的预测结果与真实值的对比如图7所示.从图7中可以看出,两种神经网络的预测精度都很高,尤其是衰减域频率范围和低频区能量传递系数与真实值吻合得很好,仅图7(d)中RBF神经网络的预测结果稍偏离了真实值.测试集中两种神经网络预测误差的统计图如图8所示.其中:J为样本数.由图8可知,深层BP神经网络的预测效果更好.

图7 能量传输谱预测值与真实值对比(30个测试样本中的4组)Fig.7 Comparison of predicted values of energy transmission spectrum with real values (4 groups out of 30 test samples)
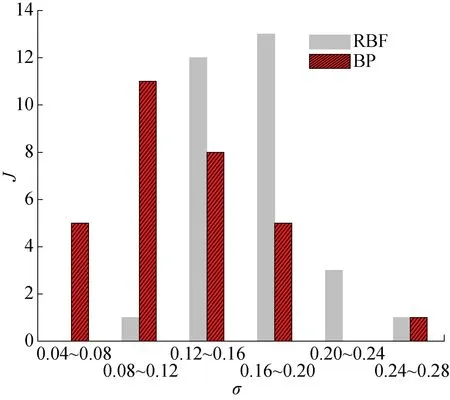
图8 两种神经网络预测值的误差统计(30个测试样本)Fig.8 Error statistics for two neural network predictions (30 test samples)
3.3 三参数变化
三参数变化时,数据集由训练集 III 和测试集 III 组成.RBF神经网络的结构为“3-1 000-100”;深层BP神经网络为“3-300-100-80-80-80-80-60-60-60-60-100”,共10个隐含层.测试集 III 中4组神经网络的预测结果与真实值的对比如图9所示.从图9中的4组结果可以看出,深层BP神经网络的预测值与真实值吻合得较好,但是RBF神经网络的预测结果出现了极大的偏离.测试集中两种神经网络预测误差的统计图如图10所示.从图10中可以看出,RBF神经网络的预测精度极不稳定,300组测试样本中接近一半的预测结果误差大于0.50,其中最大误差达到18.35;而深层BP神经网络依然发挥着很好的性能,最大误差仅为0.33,90%的样本误差落在(0.14,0.26).
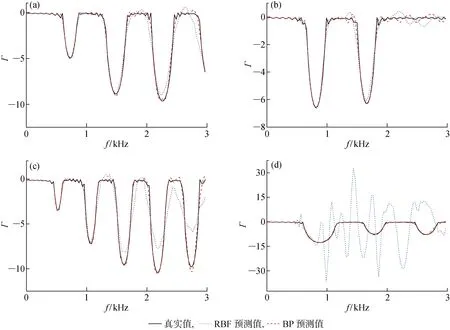
图9 能量传输谱预测值与真实值对比(300个测试样本中的4组)Fig.9 Comparison of predicted values of energy transmission spectrum with real values (4 groups out of 300 test samples)
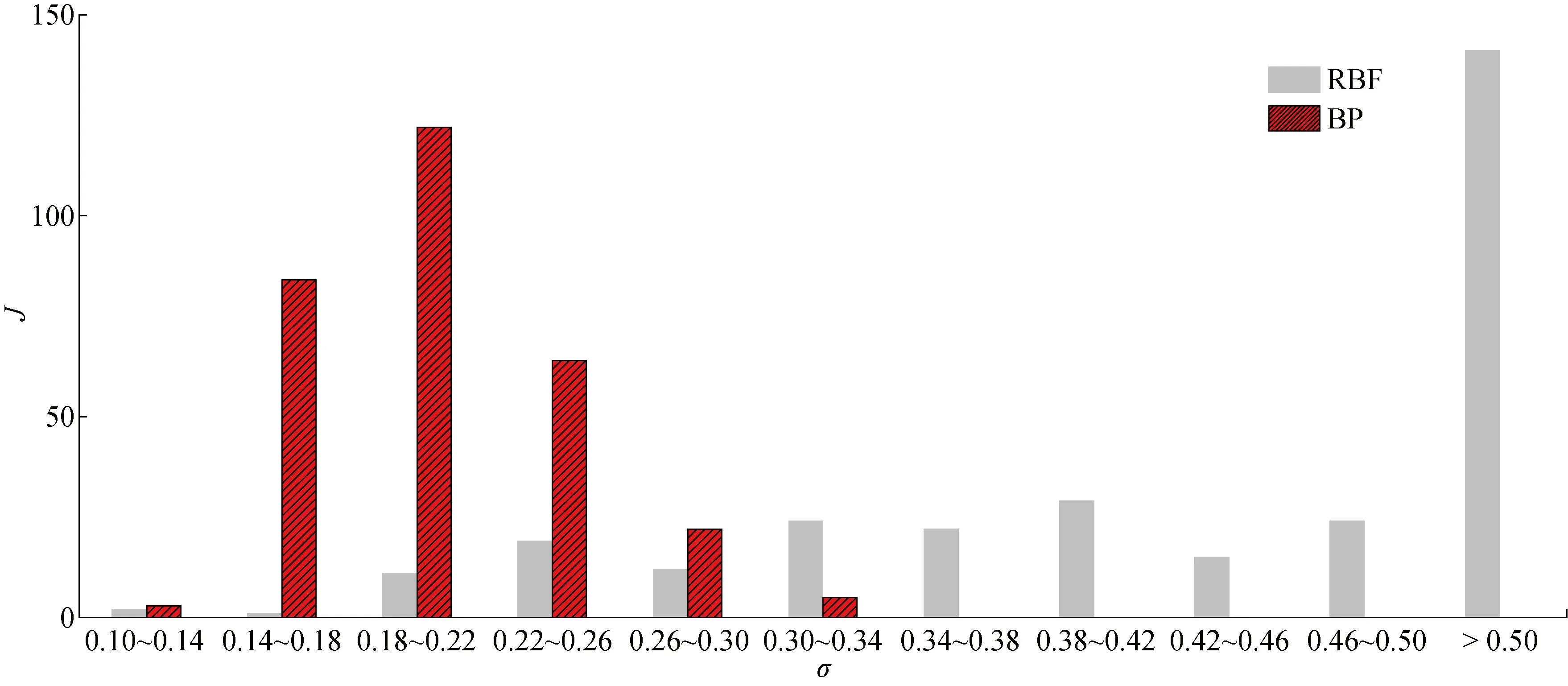
图10 两种神经网络预测值的误差统计(300个测试样本)Fig.10 Error statistics for two neural network predictions (300 test samples)
4 结语
通过构建深层BP神经网络,实现了层状周期结构能量传输谱的精准预测,分别考虑了几何参数和物理参数单独变化及同时变化3种情况并与RBF神经网络进行了对比.研究结果表明:当仅考虑填充比变化时,两种神经网络的预测精度较高,且性能相近;当考虑切变模量比和密度比同时变化时,两种神经网络的预测结果都较好,但深层BP神经网络的性能更优;当同时考虑填充比、切变模量比和密度比变化时,两种神经网络的表现差异很大.深层BP神经网络预测精度高且性能稳定,预测误差范围为0.10~0.34;而RBF神经网络的预测精度极不稳定,其测试集样本的预测误差范围为0.10~18.35,其中接近一半的误差超过0.50.
利用神经网络实现周期结构的正向预测是实现其反向设计的前提.传统的周期结构反向设计的方法是将机器学习与解析法或数值法结合,比如遗传算法结合有限元法.由于解析法和数值法计算较慢,采用以上方法设计一个周期结构所需的时间较长.若用神经网络替代解析法或数值法,即可以结合遗传算法和神经网络,用神经网络辅助计算遗传算法中个体的适应度,这将能省去大量的计算时间.
通过神经网络实现了层状周期结构能量传输谱的智能预测,对于不同的几何参数和物理参数,BP神经网络均可以快速、准确地预测出衰减域的频率范围及衰减幅度,避免了大量经验性尝试所带来的计算资源消耗.神经网络预测可以作为周期结构设计的一种辅助工具,在快速准确地预测出结构传输谱的基础上,针对环境振动或地震动领域减隔振问题需求,结合遗传算法或其他方法能够快速找到符合设计要求的结构,对于减振分析及设计具有重要的意义.对于层状周期结构传输谱的成功预测也为二维和三维周期结构分析以及周期结构的智能反向设计提供了参考.

