人力资本水平与经济发展的相关性研究

文/ 苏思琦 郭学军

随着社会经济发展，人力资本越来越受关注。这是由于人力资本合理投资在经济发展中占据重要地位。人力资本投资重要性主要体现在低素质劳动转换为高素质劳动力，推动人口质量的整体提高。目前，已有学者对人力资本水平与经济发展的相关关系进行研究，并取得较好的研究成果。但在目前研究中，很少以数据清洗的方式进行研究。

一、问题分析

（一）指标选取

在现有研究中，有学者构建了方便简单的区域人力资源发展水平评价指标体系[1]，有学者建立了内部层、关联层、调控层三类指标，形成一个综合评价指标体系[2-3]。本文在相关学者研究基础上，将人力资本分为三个大类, 见表1。

表1 评价人力资本水平体系

（二）数据处理

人力资源三大指标体系：教育水平、医疗水平、研究与创新以及相应二级指标体系物理指标等存在一定差别，在数据利用时，需对数据进行处理。

1. 数据来源。本文选取《国家统计年鉴》（1999-2018）中，与人力资本有关的各项数据。

2. 数据预处理。 我国医疗机构2002 年的数据为1005004 个，到2003 年突然下降到806243 个，有理由怀疑存在一定异常值。假设医疗卫生机构变量服从正态分布，t检验准则决定离群点取舍。T 检验统计量为：

其中，xd为离群点，第j 个变量的平均值xj和标准差Sj。

其中，

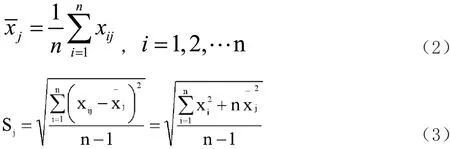
医疗卫生机构不含离群点的平均值和标准差分别为：

在显著水平0.01 条件下，离群点不在拒绝域中，保留此离群点。

二、模型建立

（一）因子分析模型

经数据清洗处理后，选取10 个主要指标作为人力资本水平。为消除量纲影响，对数据进行标准化处理。第j 个指标或者变量标准化，即：

其中，xij表示第j 个变量的第i 次观测，表示xij标准化后的值。经过标准化数据的相关系数矩阵判断变量的相关程度。相关系数矩阵ρ的第i行第j列元素计算公式为：

经计算得到多数变量之间具有较强相关性，且各指标之间的信息重叠也很多。因此，将这10 个变量综合成几个少数变量，这里进行R 型因子分析。

初始特征值第一列为特征值，第二列为方差贡献率，第三列为累计方差贡献率。前两个累计方差贡献率已达到97.336%，选三个公共因子包含的原始数据的绝大部分信息。由原来10 个变量转换成2 个综合变量，在此基础上，计算综合因子。第一个因子的权重：

表2 综合排名

表3 中第一因子排名基本和综合排名相同，这是由于第一因子对综合得分贡献最大。从得分排名可看出，2004 ～2015 顺次由低到高，符合社会经济发展实际情况。从整体上看，中国经济一直高速发展，但2003 年排名发生逆转，该年国内暴发非典型性肺炎，经济发展受到重创，疫情结束后，再次转向经济建设。2010 年，上海世博会举行，成为走向世界又一个重大契机，也为刚经历金融危机的中国带来发展机会。

（二）GDP 模型

GDP 是衡量经济发展重要指标，根据因子分析建立其模型，进行预测非常重要。

1.GDP 模型构建

设Y 表示随机变量GDP，用因子分析模型得出的得分矩阵作为设计矩阵，公共因子为一般变量。建立随机变量Y 与一般变量F1,F2的线性回归模型为：

经计算得P 值近似为0，说明回归方程系数显著，F1、F2对Y 具有显著影响。F 统计量服从自由度为(2,14) 的F分布，在显著水平为0.05 的条件下，查表的F 临界值为3.74，F 统计量大于临界值，据此可以认定回归方程显著。

2.GDP 模型预测

利用建立的回归模型预测2016 年～2018 年的GDP，与实际GDP 进行对比，以检验模型是否可靠。2016 年实际GDP 为1.31013，置信水平为0.05 条件下点估计值为1.34357， 预 测 区 间 为[1.20512，1.48202]。2017 年 实际GDP 为1.61595，置信水平为0.05 条件下点估计值为1.62606， 预 测 区 间 为[1.41827，1.83386]。2018 年 实际GDP 为1.91745，置信水平为0.05 条件下点估计值为1.85973，预测区间为[1.37900，2.34046]。点估计值与实际值相差并不大，且都在预测区间内，此时认为模型可靠准确，可后续预测。

三、结果分析

从GDP 回归模型中可以明显地看出，GDP 与第一因子和第二因子均相关，但与第一因子相关关系更强，这说明教育、医疗和技术的投入越多，GDP 值越大，经济发展水平越高。要进一步提高人力资本水平还要加大对教育的投入。教育投资不仅可以提高人们文化水平和生活品位，而且可以使受教育者在现代社会发展和激烈的竞争中掌握一定技能。