某混合动力总成系统静刚度设计研究
张远亮,张立民
(1 四川城市职业学院 智能制造与交通学院,成都610110;2 西南交通大学牵引动力国家重点实验室,成都610031)
利用弹性元件将车体与车下设备连接起来组成的单层隔振系统,对振动、噪声要求比较高的设备已经无法满足设计要求。目前,有关设计工作者开始深入、系统的研究双层隔振系统,已满足设计要求[1−4]。
对车下隔框架、机组及动力冷却包建立动力学平衡方程,同时满足几何协调平衡,在满足一级、二级隔振器垂向变形量容许的条件下,筛选出框架和机组的转动角度绝对值不小于0.02 度且不大于0.04 度的刚度组合工况,同时结合实际情况,得到了满足设计要求的各个隔振器静刚度值;将设计值静平衡验证,各项位移量及偏转角均符合要求,设计结果可靠。为后续仿真及振动性能等提供借鉴及依据,对工程中车下设备悬挂刚度设计具有指导意义[5−11]。
1 混合动力总成系统简介
研究对象为某型混合动力动车组动力包总成系统。动力总成通过4 个隔振器安装在车体下方,如图1 所示。
动力总成将柴油发电机组2、散热器3 等集成在框架上,如图2。
本系统中动力总成是双层隔振系统,柴油发电机组与框架之间连接的隔振器定义为一级隔振器组,框架与底部连接的隔振器定义为二级隔振器组。动力包隔振系统的各个隔振器的位置和编号如图3。
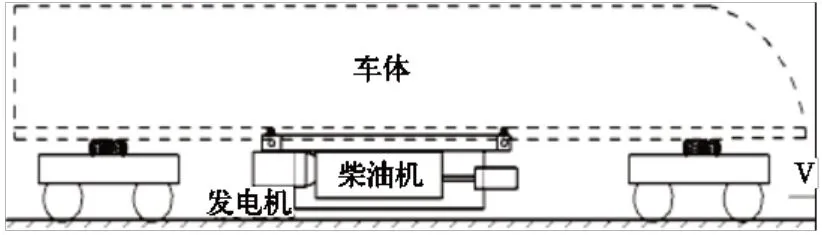
图1 某混合动力总成悬挂示意图
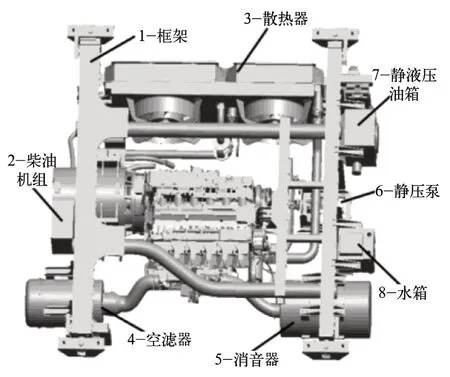
图2 动力总成组成
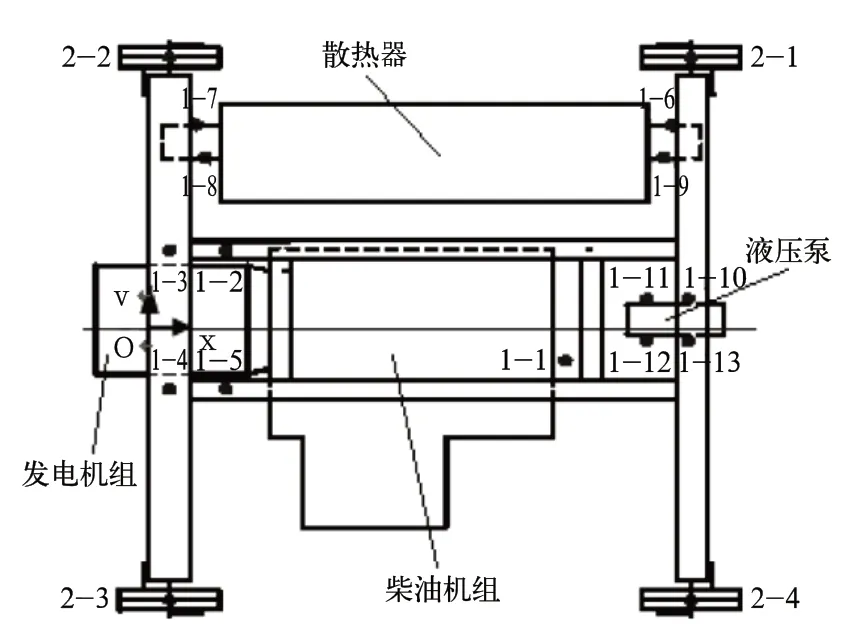
图3 隔振器位置和编号
2 静刚度设计分析
2.1 动力包静平衡模型
根据动力包实际模型,画出动力包框架、机组和冷却装置各隔振器位置示意图如图4 所示,其中以车体中心线与框架2 位端上端面的交点为坐标原点。
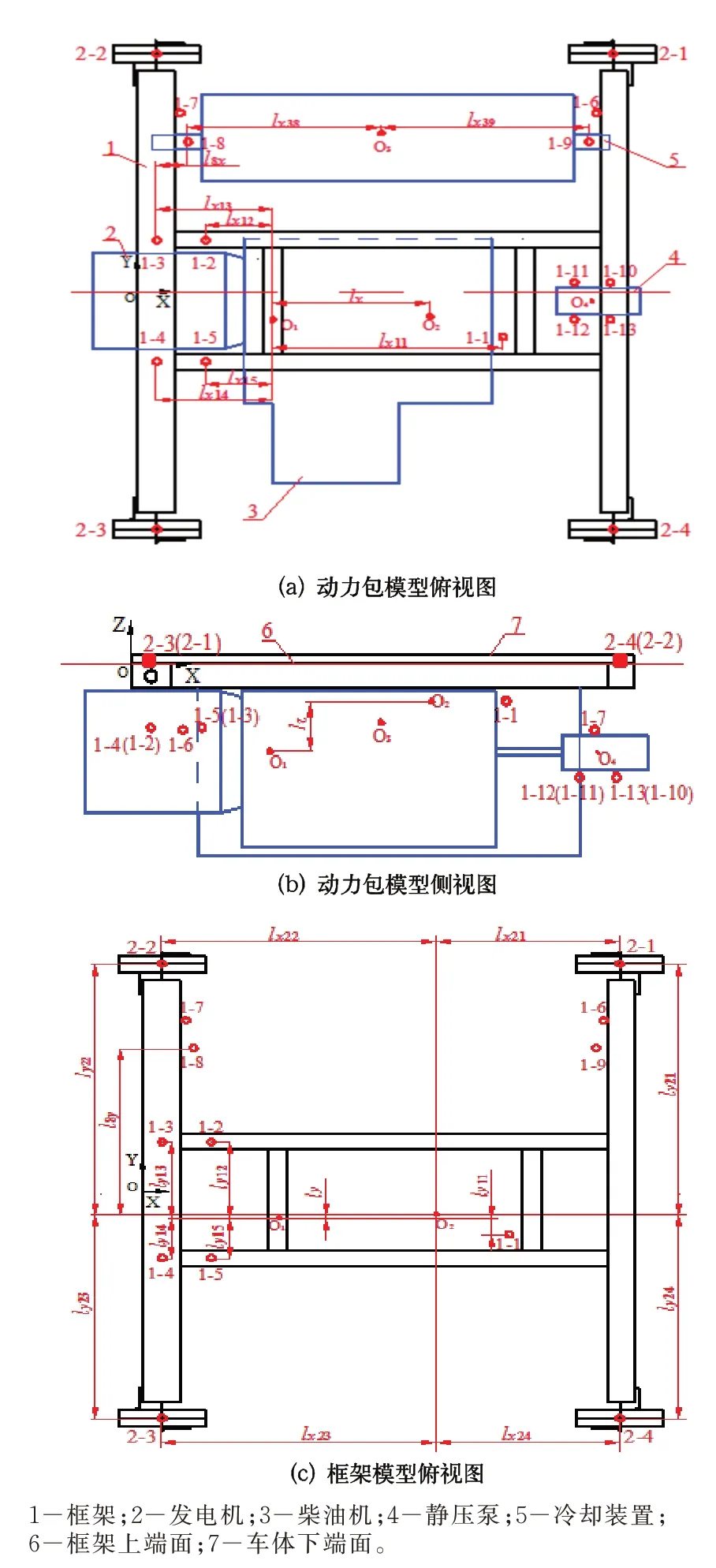
图4 动力包静平衡模型简图
2.2 基本参数
系统中质量及质心位置见表3 及表4。
2.3 设计过程
对模型进行分析,分别对各部件建立方程组。
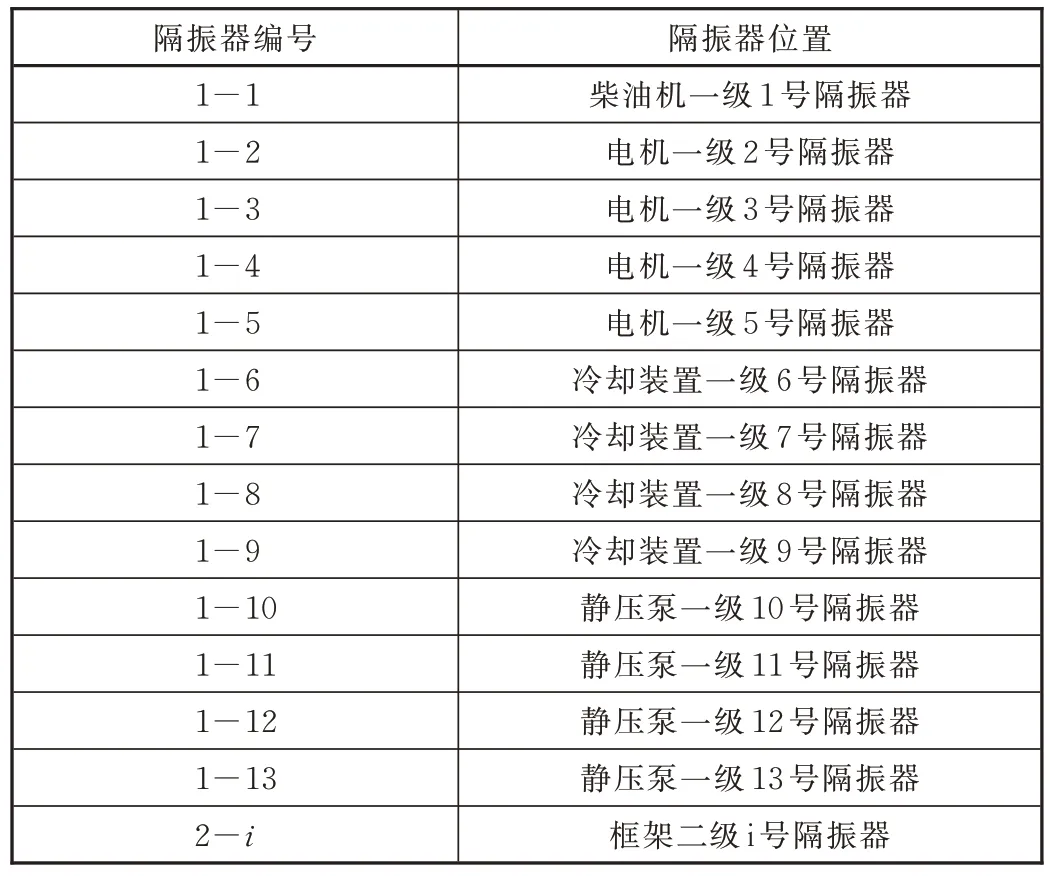
表1 动力包模型各隔振器符号物理意义
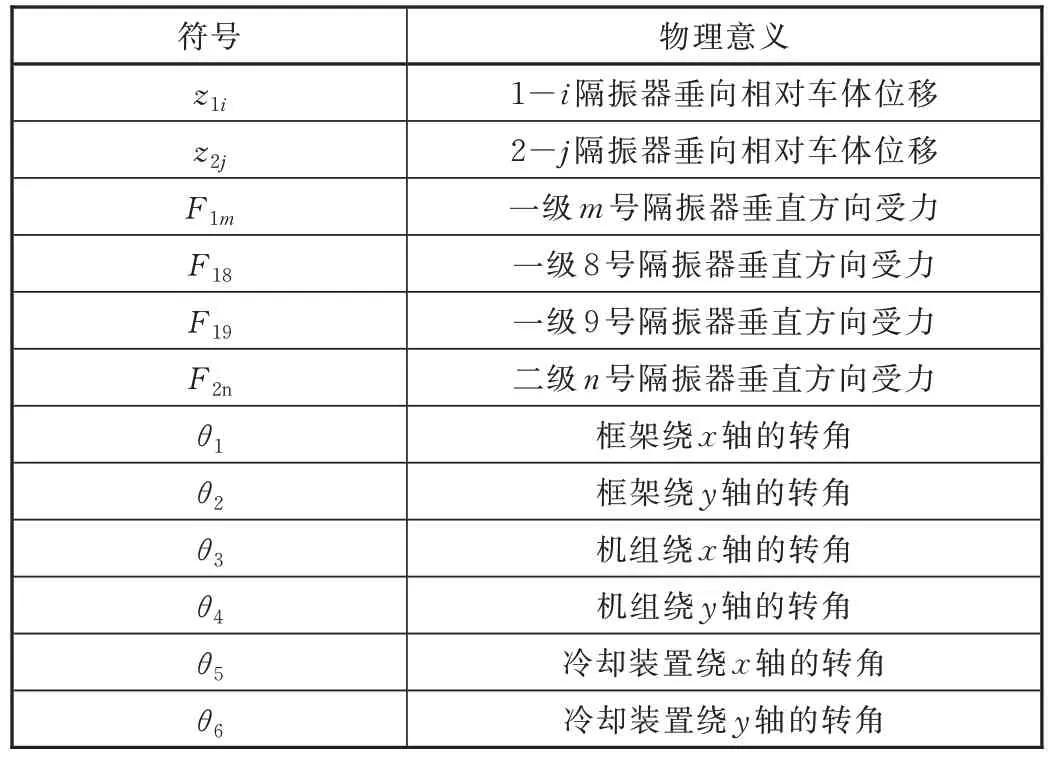
表2 动力包数学模型各参数符号物理意义
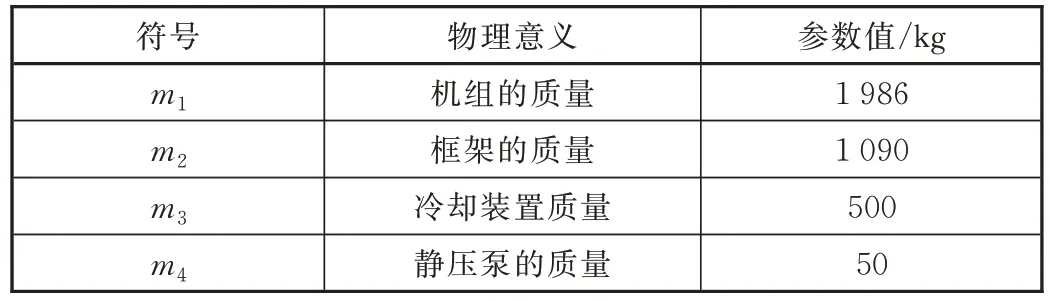
表3 动力包模型质量参数
对于框架:受力如图5 所示。
根据力和力矩平衡列方程如式(1).
力的平衡方程
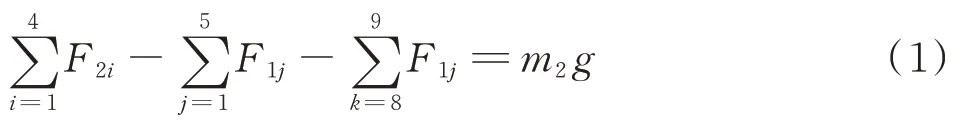

表4 动力包模型各标注参数尺寸
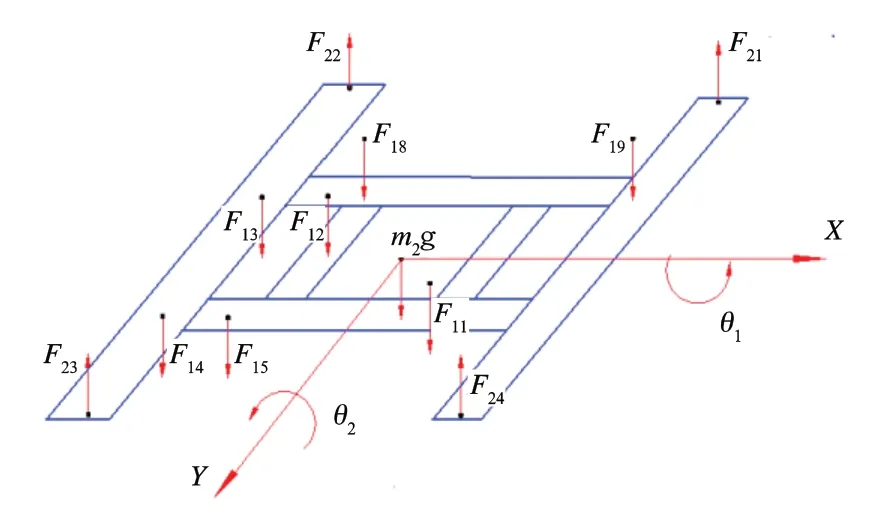
图5 动力包框架受力图
以F22和F23所在直线为转动轴列出力矩平衡方程式(2)
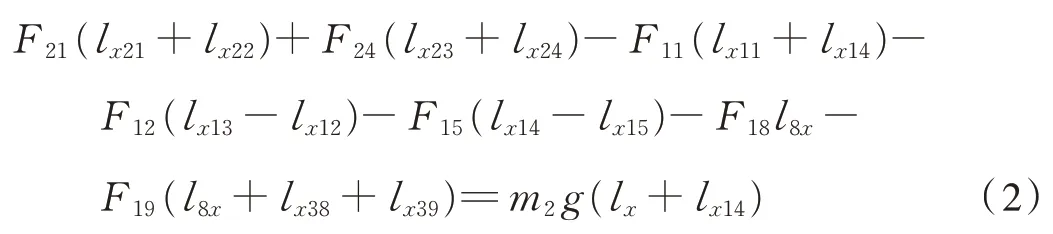
以F23和F24所在直线为转动轴列出力矩平衡方程式(3)

根据二级隔振器共面条件列出几何协调方程式(4)
由于本系统采用两路信号同时滤波,且为达到尽可能理想的滤波器及处理性能与FPGA逻辑资源之间的平衡。本系统利用FIR滤波系统在具备线性相位时的对称特点,采用对称结构对此滤波器进行实现,以减少对乘法器资源的使用以及尽量增大滤波器的阶数,使其更接近于理想滤波器[12-14]。

对于机组:受力如图6 所示。
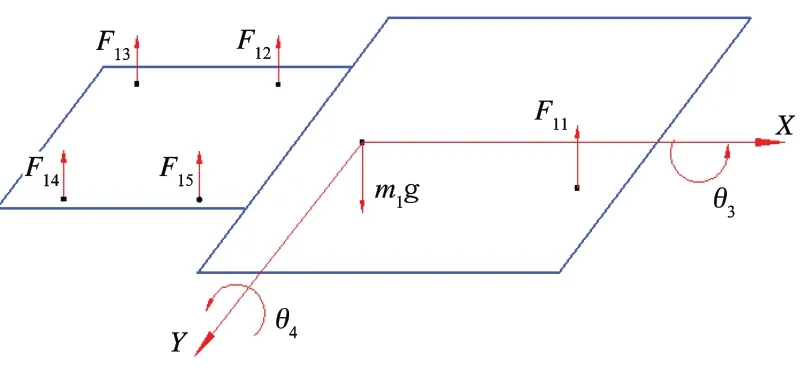
图6 动力包机组受力图
根据力和力矩平衡列方程如下:
力的平衡方程式(5)

以F13和F14所在直线为转动轴列出力矩平衡方程式(6)
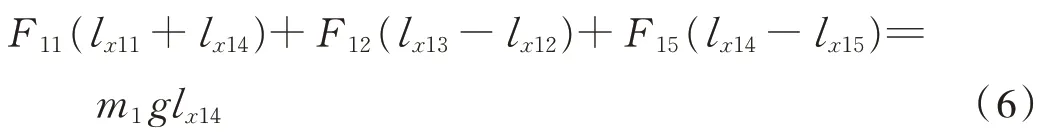
以F14和F15所在直线为转动轴列出力矩平衡方程式(7)
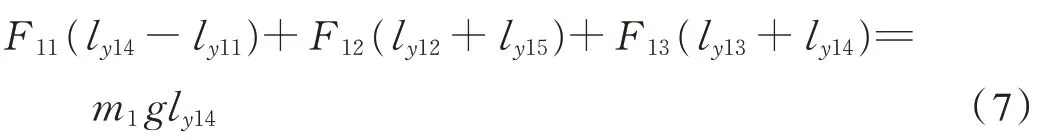
根据一级隔振器共面条件列出几何协调方程式(8)~式(9)
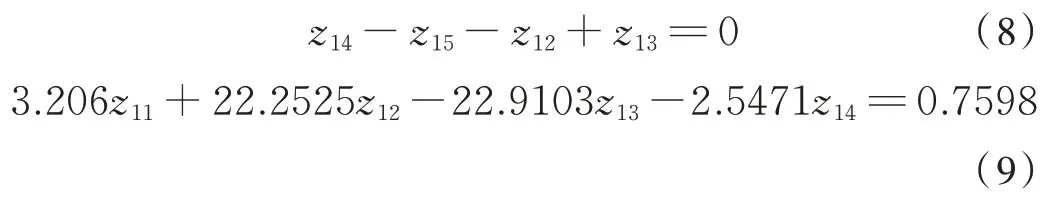
对于冷却装置:受力如图7 所示。
根据力和力矩平衡列方程如下:
力的平衡方程式(10)
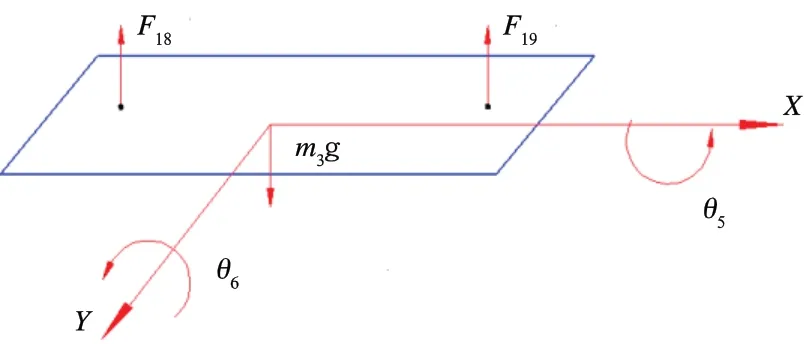
图7 动力包冷却装置受力图
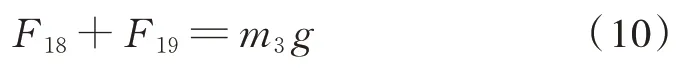
以和所在直线为转动轴列出力矩平衡方程
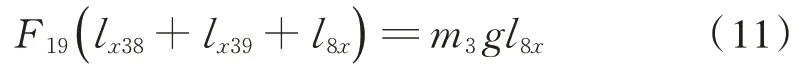
在满足二级隔振器垂向变形量5.0~6.5 mm 以及一级隔振器垂向变形量 4.0~5.0 mm 的条件下[11−13],求解方程式(1)~式(11)。根据工程实际情况以及隔振器压缩量(变形量)要求,在全部解集中筛选出框架和机组的转动角度绝对值不小于0.02°且不大于0.04°的刚度组合工况,结果如图8~图12 所示。
2.4 设计结果
由上述分析得符合静平衡条件的垂向静刚度工况如表5 所示。
在表5 的37 组刚度组合中,最终选取的静刚度值见表6。
将选取的静刚度值进行静平衡验证见表7。(取各刚体垂直向下为正位移方向)。
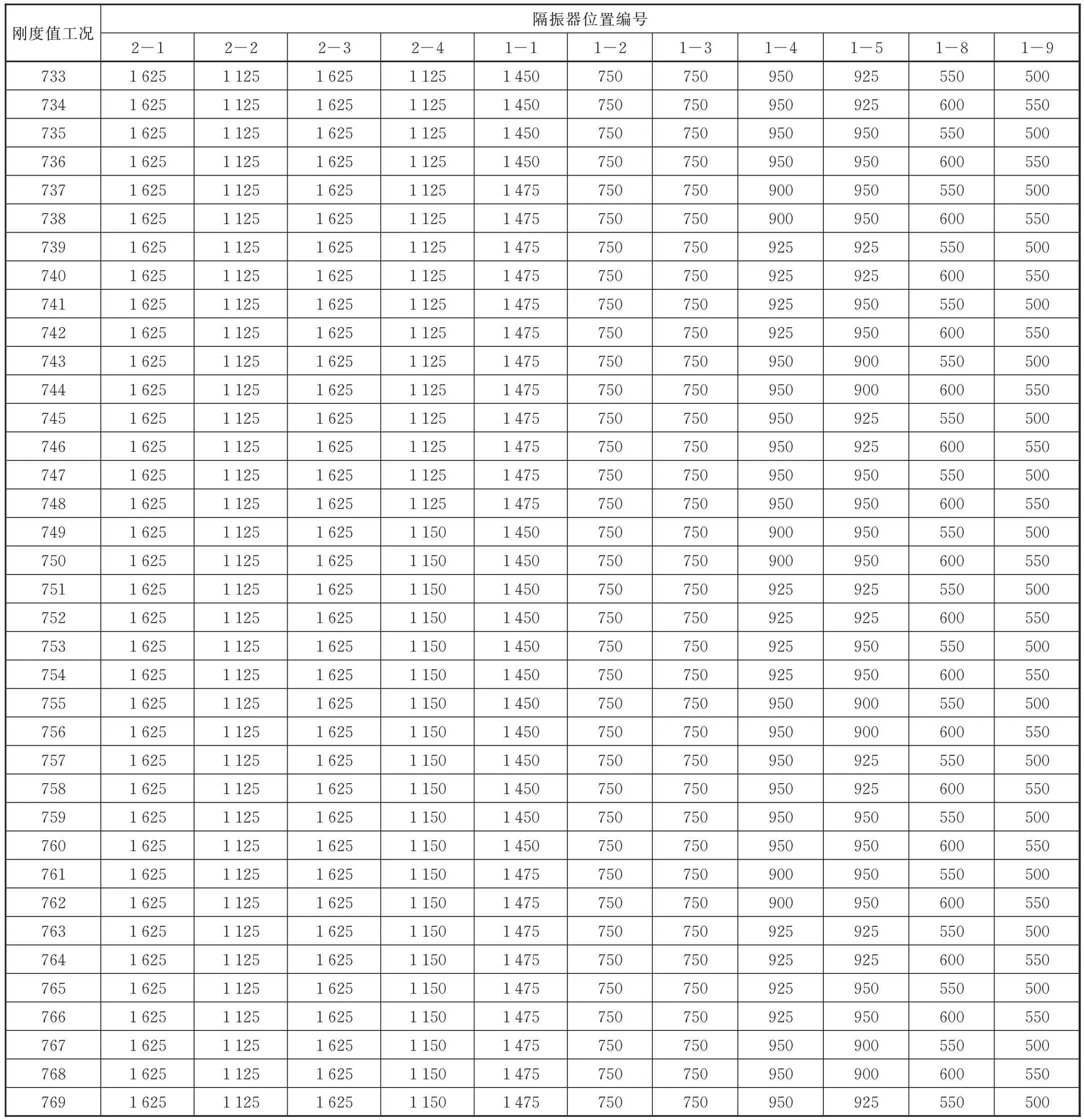
表5 符合静平衡条件的垂向静刚度工况 N/mm

表6 静刚度设计选取的静刚度值 N·mm-1
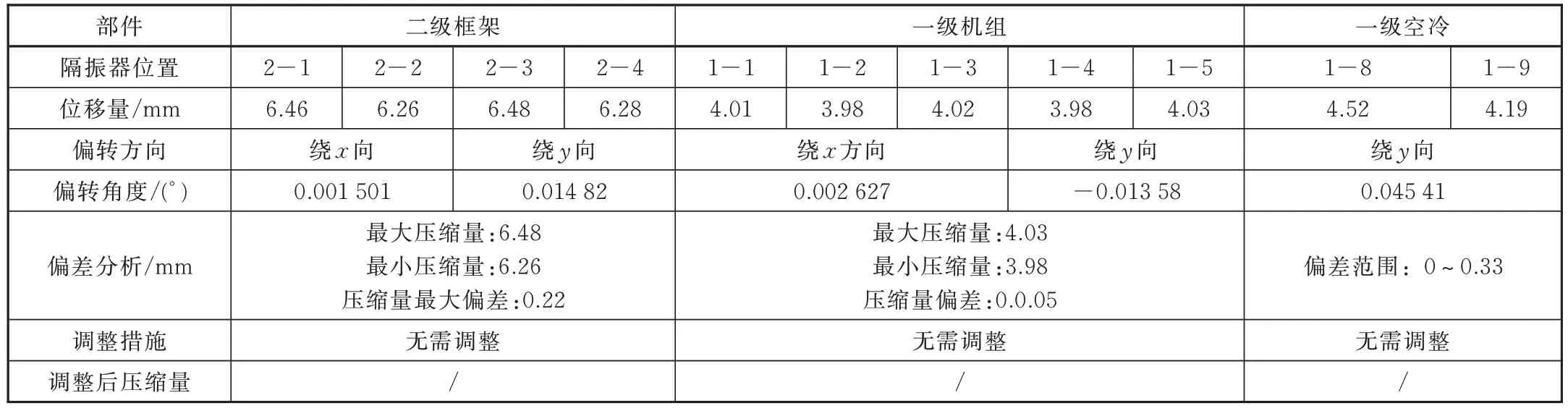
表7 静平衡验证 (刚度比1.6)
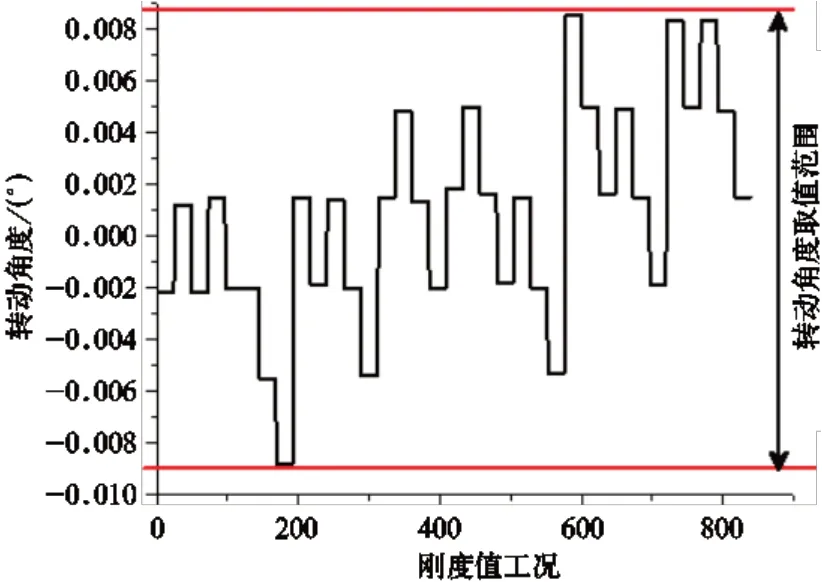
图8 框架绕X 轴转动角度与工况关系
3 结 论
通过以上分析得到如下结论或方法:
(1)车下隔框架、机组及动力冷却包除了满足动力学平衡外,还需要满足几何协调平衡,这是一个超静定平衡问题。
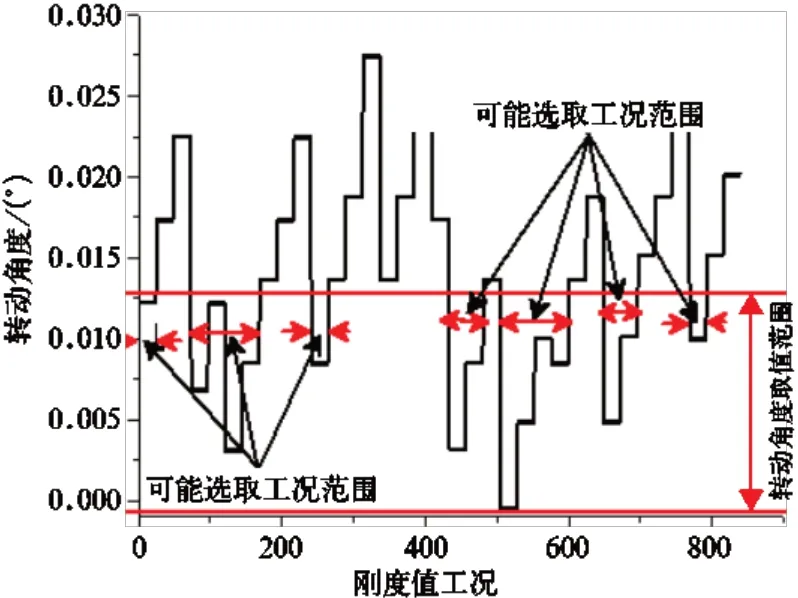
图9 框架绕Y 轴转动角度与工况关系
(2)在满足二级隔振器垂向变形量5.0~6.5 mm 以及一级隔振器垂向变形量4.0~5.0 mm 的条件下,筛选出框架和机组的转动角度绝对值不小于0.02°且不大于0.04°的刚度组合工况,同时结合实际情况,得到了满足设计要求的各个隔振器静刚度值。
(3)将设计值静平衡验证,各项位移量及偏转角均符合要求,设计结果可靠。
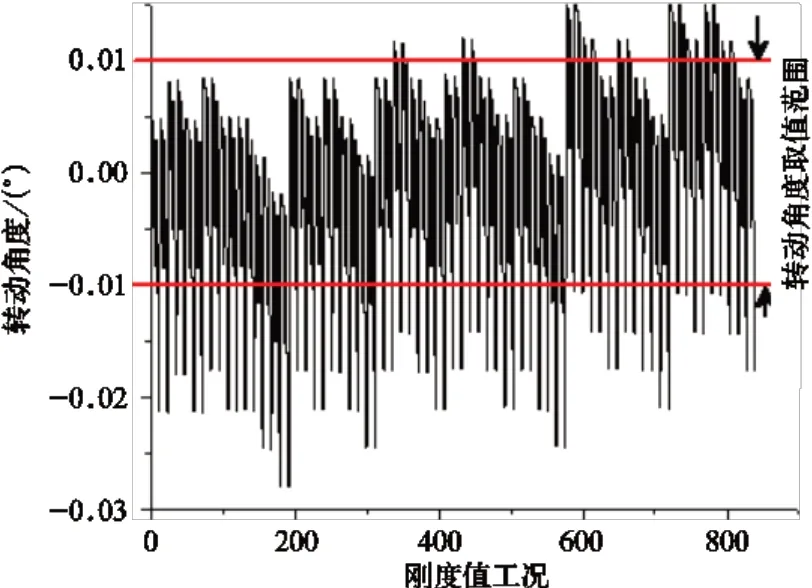
图10 机组绕X 轴转动角度与工况关系
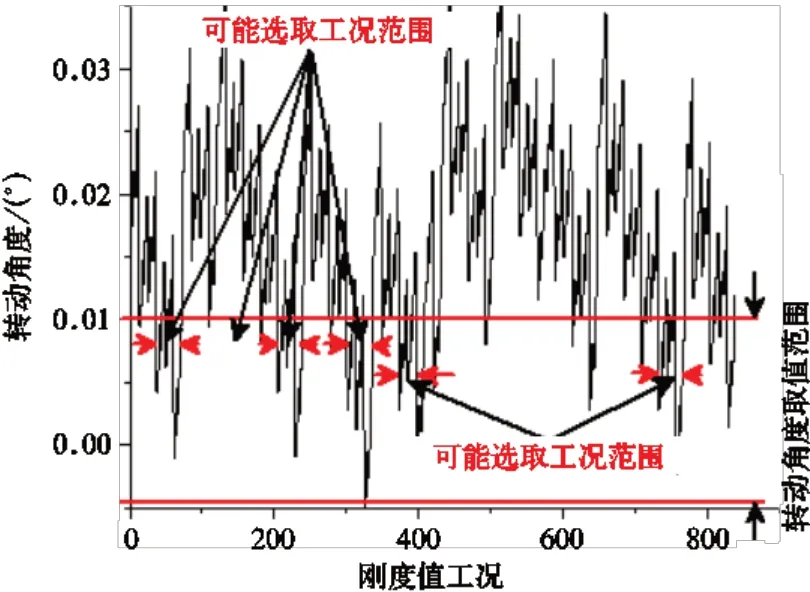
图11 机组绕Y 轴转动角度与工况关系
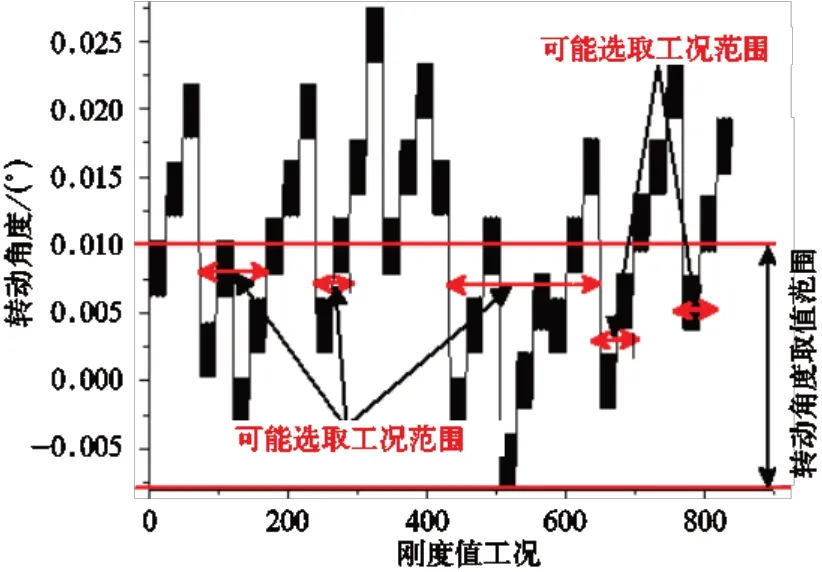
图12 冷却绕Y 轴转动角度与工况关系

