车载电力电子变压器的高频隔离DC-DC 变换器双相移控制*

赵 震 ，刘 洋 ，马 驰 ，谢冰若 ，王永翔

（1 中国铁道科学研究院集团有限公司 机车车辆研究所， 北京100081；2 北京纵横机电科技有限公司， 北京100094）

随着我国经济进一步发展，铁路行业飞速发展，轻量化和高功率密度化成为铁路发展的主要方向，这对列车牵引系统提出了新的挑战。为了实现小型轻量化的列车牵引系统，文献[1]提出了一种无工频牵引变压器的交流传动系统拓扑，如图1 所示。其中双有源全桥隔离 DC-DC 变换器(Dual Active Bridge， DAB)因其工作频率高、传输功率高、功率密度高、能量可双向传输、易实现软开关以及高可靠性等优点[2]，在分布式微电网、电动汽车以及列车牵引系统等得到了广泛的使用[3]。

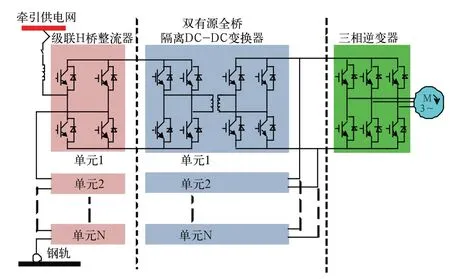
图1 无工频牵引变压器的交流传动系统

DAB DC-DC 变换器作为新型牵引系统中的关键环节，其控制方法决定着整个牵引系统的工作效果以及整体效率[4−6]。对于 DAB DC-DC 变换器，常用的控制方法为相移控制[7−9]。

相移控制方法是DAB DC-DC 变换器普遍采用的控制方法。在单相移控制(Single phase shift， SPS)方法中，通过占空比为50%的驱动信号，达到控制双有源全桥隔离DC-DC 变换器的目的。但在SPS 控制方法下，若变换器输入输出电压不匹配，变换器工作时存在回流功率现象，导致功率器件的电流应力增加，变换器的传输效率降低[10]。

为了进一步提升DAB DC-DC 变换器的工作效率，采用了双相移控制(Dual phase shift， DPS)方法，建立了变换器在DPS 控制下的数学模型，分别分析了在SPS和DPS 控制下的变流器回流功率特性，通过仿真与1 kW 样机试验对SPS 和DPS 两种控制的性能进行了对比分析研究。

1 DAB DC-DC 变换器工作原理

1.1 相移控制方法

图2 为DAB DC-DC 变换器的电路拓扑。其中，S1−S8代表 8 个开关管，T 是高频隔离变压器，L是变压器原边漏感和辅助电感之和，RL是电路所带负载，vH1是原边桥臂间电压，vH2是副边桥臂间电压，Us为输入电源，Uo为输出电压，iL为电感电流并规定图示方向为电感电流参考方向。

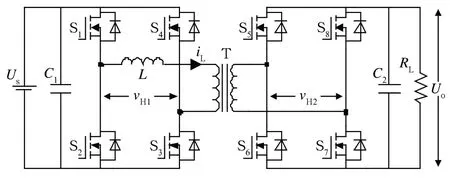
图2 DAB DC-DC 变换器拓扑

文中所采用的控制方法为SPS 控制与DPS 控制方法，DAB 变换器两个全桥对管之间存在相同的内相移比D1，两个全桥的交流输出电压vH1和vH2之间存在外相移比D2，仅讨论 0＜D1＜D2＜1 且D1+D2＜1 的情况。

图3 为所采用两种相移控制方式时序图。其中，D1为内相移，D2为外相移，Ts代表开关周期，iL代表电感电流，S1、S3、S5、S7代表对应开关管的驱动信号。由图 3 可知，变压器原副边波形为三电平波。通过控制D1和D2，就可以控制变换器传输功率的大小和方向。

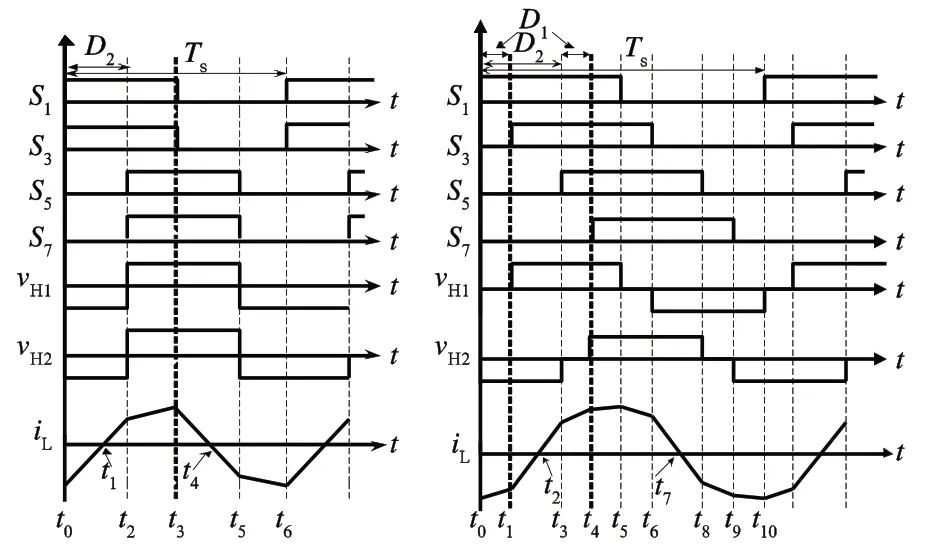
图3 相移控制时序图

1.2 变换器数学模型

以DPS 控制为例，对变换器在DPS 控制方法下的工作状态进行化简，如图4 所示。

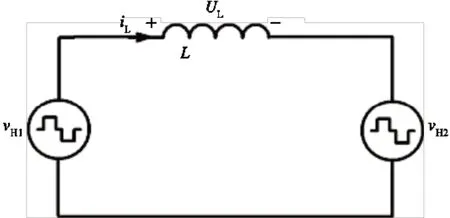
图4 DAB DC-DC 变换器简化电路

在分析过程中，不考虑电路元件的损耗，假设所有元件均工作在理想状态，设变压器变比为1：1。由图4可知，电感电压及输入输出电压的关系为:

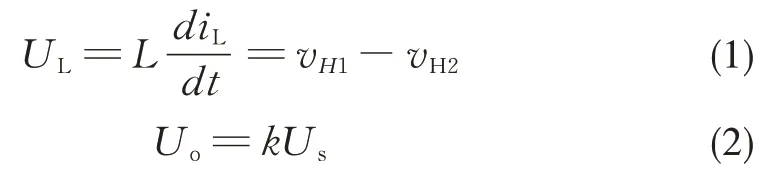
式中，k为输出电压与输入电压之比，且0≤k≤1，即变换器仅工作在降压模式下。当变换器调制方法为DPS控制时，结合上述电路各阶段工作原理可得:

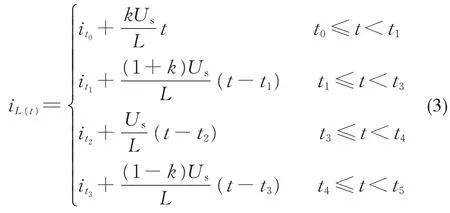
当变换器工作状态稳定时，电感电流在半个开关周期内关于过零点旋转对称且连续，由此建立电感电流之间的关系:

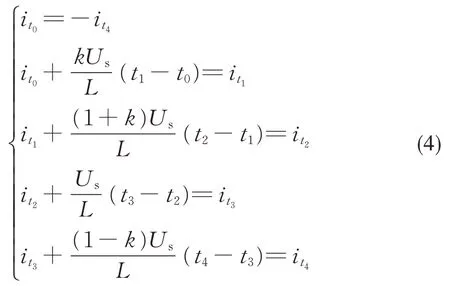
由式(3)和式(4)，可得不同时刻对应的电感电流值:

将式(5)代入式(3)可得:

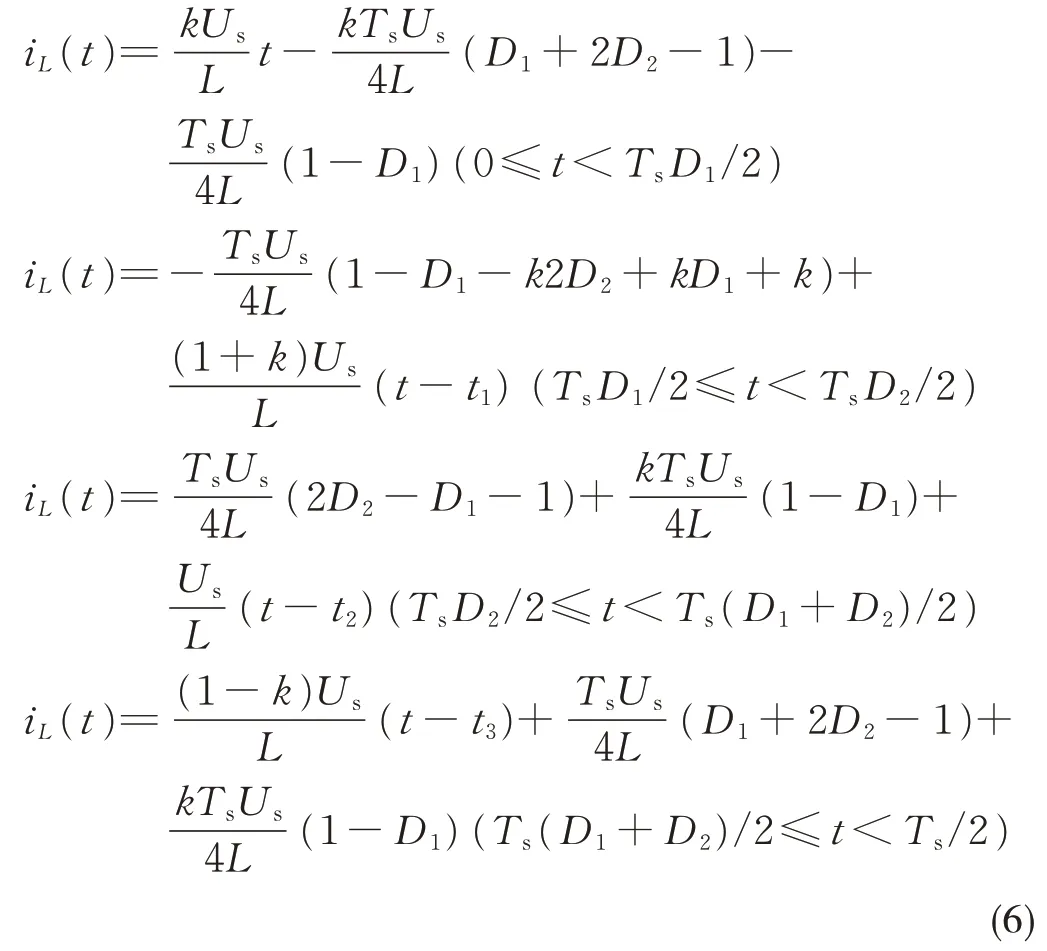
DAB DC-DC 变换器的功率计算公式为:

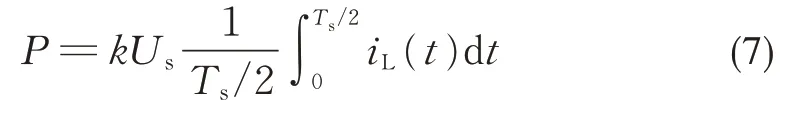
将式(6)代入式(7)可得 DPS 控制下 DAB DC-DC 变换器的传输功率数学模型:

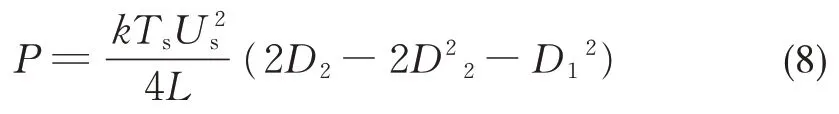
式中 0≤D1≤D2≤1 且D1+D2≤1。

将式(8)中DPS 控制內相移值设为0，能够得到SPS控制下的传输功率数学模型:

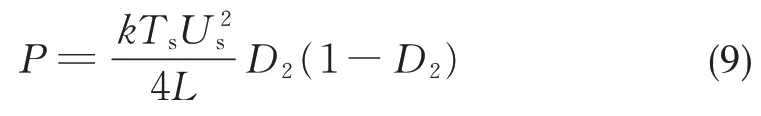
2 DAB DC-DC 变换器回流功率模型建立及控制方法分析

2.1 回流功率建模

在变换器工作过程中，由于电感电流iL不可突变的特性，在电感两端电压变化后，电感电流方向仍保持原方向，导致电感向电源释放能量，这个现象称之为功率回流现象。由于这个现象的存在，能量无法从电源侧向负载侧传递，而是回流到电源侧，因此称这部分功率为回流功率。

在DPS 控制方法下，变换器在t1～t2阶段，存在功率回流现象，即电感电流方向与电感电压方向相反，能量回流到电源侧。DPS 控制下变换器回流功率示意图如图5 所示，图中功率回流过程使用阴影标出。

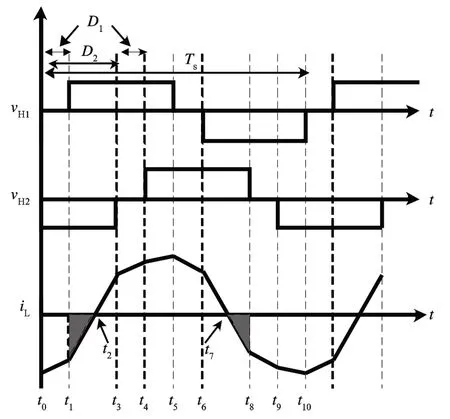
图5 DPS 控制回流功率示意图

由图5 可知，在变换器工作时，功率回流现象呈周期性出现，因此选取半个工作周期为时间单位进行公式推导与模型建立。回流功率是在电感电流方向与电压方向相反时出现的，其大小能够通过积分来进行确定，设回流功率为Qdpc，则其能够表示为:

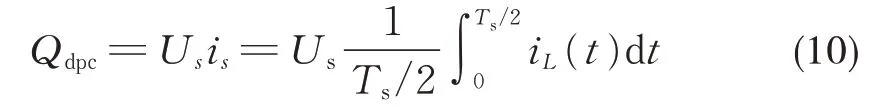
由式(10)可以推出，当电感电流上升到零时，时间t2为:

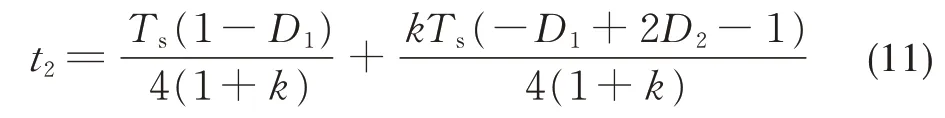
将t1=D1和式(11)代入式(10)，可得:

式中负号表示这部分功率相对于电源输出功率为负，即回流功率。

在SPS 控制中，代入D1=0，可得SPS 控制下变换器回流功率为:

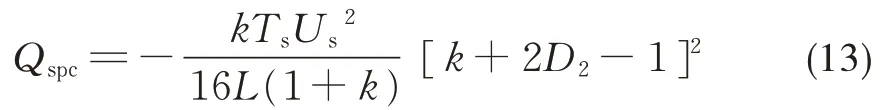
由式(12)可知，回流功率与电感大小、相位差取值、变压器变比和工作周期这4 个量有关。为了降低变换器回流功率，应当选择合适的D1、D2的组合，使得电路的回流功率尽量小。

2.2 回流功率分析

为了分析两种控制方法下回流功率特性，基于Matlab 软件绘制出两种控制方法下传输功率模型图，如图6 所示。设p为标幺化的变换器传输功率，选取p=0.5 和p=0.6 两种情况下的工作点进行观察。

为了明确回流功率与变换器输出功率之间的关系，定义回流功率比为:

在p=0.5 时，采用 SPS 控制方法的A点D2=(2 −控 制 方 法 下A1 点D1=D2=1/6，A2 点D1=D2=1/2。将这些工作点代入回流功率比公式，得到两种控制方法下回流功率比变化图，如图7 所示。在p=0.6 时，采用 SPS 控制方法的B点对应D2=(5 −控 制 下B1点点将这些工作点代入回流功率比公式，得到两种控制方法下回流功率比变化图，如图8 所示。

由图7 与图8 可知，不论输出电压变比k如何变化，当输出功率相同时，DPS 控制下变换器的回流功率始终小于SPS 控制下变换器的回流功率。因此DPS 控制能够减小系统的回流功率，提升系统效率。通过对两种控制方法下变换器回流功率分析可知，与SPS 控制相比，DPS 控制能够减小变换器回流功率，提升变换器工作效率，因此选择DPS 控制方法作为样机控制方法。

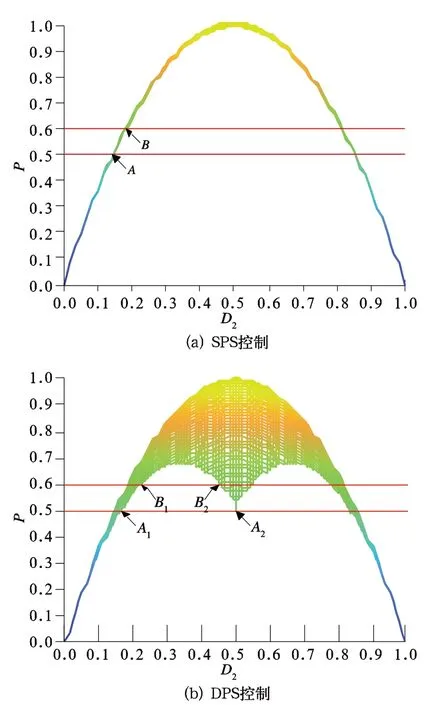
图6 两种控制方式下的传输功率模型图

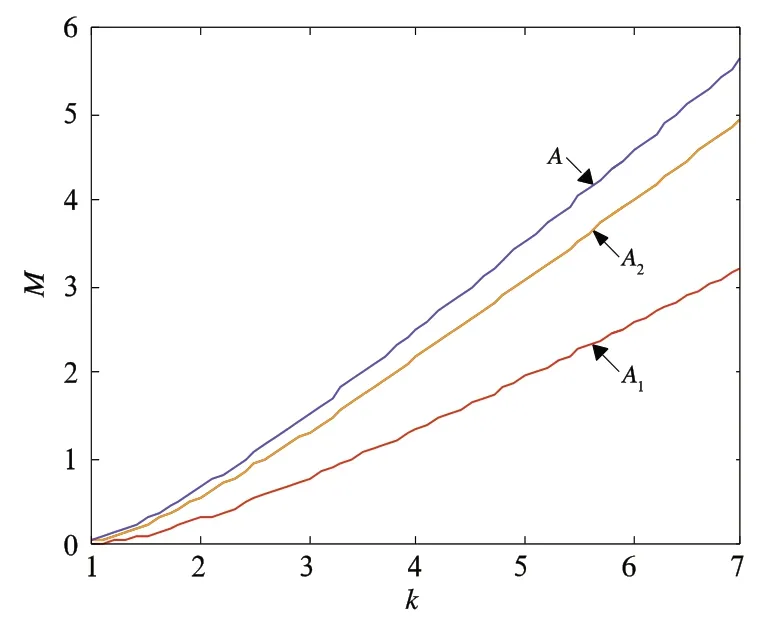
图7 p=0.5 时回流功率比变化图

2.3 仿真分析

基于Matlab/Simulink 软件对两种控制方法进行仿真，两种不同控制方法下回流功率对比如图9 所示。其中，红色部分代表变换器回流功率。

SPS 控制下变压器原副边电压波形为两电平波，在DPS 控制下变压器原副边电压波形为三电平波，这与之前中分析得到的工作时序图相同，表明变换器在两种控制方法下工作正常。DPS 控制下变换器回流功率小于SPS 控制下变换器回流功率，这与回流功率特性分析结果一致，验证了理论分析的正确性。

图8 p=0.6 时回流功率比变化图

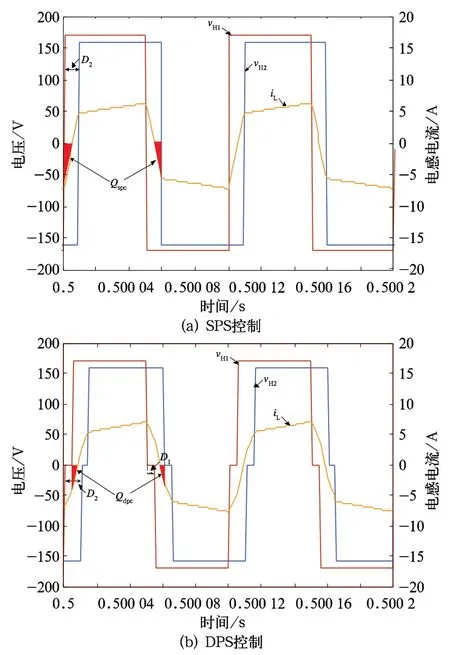
图9 两种控制方法下回流功率对比

3 试验结果及分析

以TMS320F28335 为控制系统搭建了基于SiC 的DAB DC-DC 变换器试验样机，其主要参数如表1 所示。试验样机由驱动模块、高频隔离变压器、滤波模块、检测模块以及控制模块组成，开关管采用CREE 公司型号为C3M0065090 的 SiC MOSFET。

样机采用SPS 及DPS 控制方法进行控制。其中，外环相位差由电压闭环PI 调节得到，内环相位差为给定值。试验样机的控制框图如图10 所示。

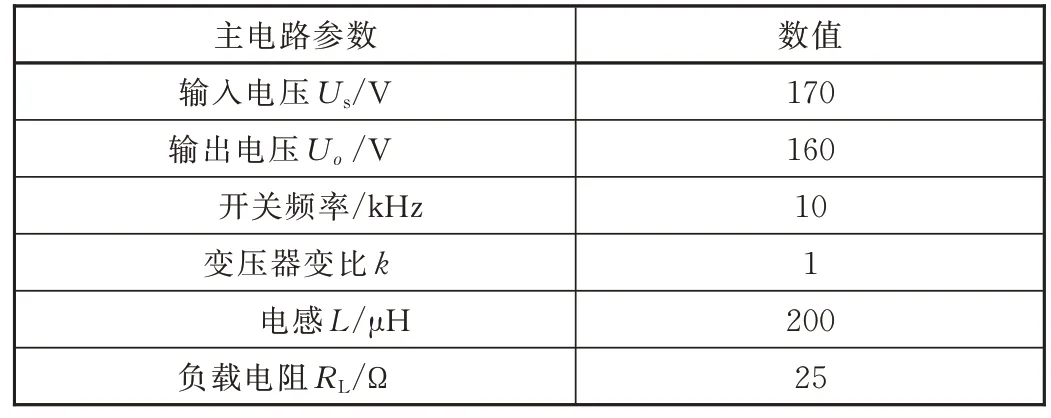
表1 试验样机参数

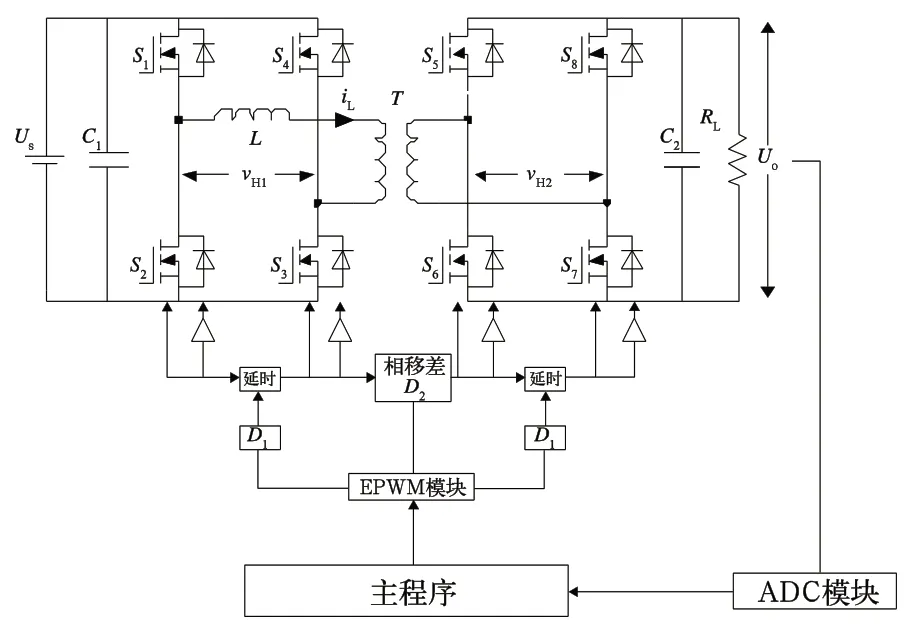
图10 样机控制框图

图11 为SPS 控制下变换器闭环控制时工作波形，此时变压器两侧波形为两电平波，变换器工作波形与理论分析及仿真模型中一致。

图11 SPS 控制对应的变流器工作波形

图12 为DPS 控制下变换器闭环控制时工作波形，此时变换器输出功率为1 kW，即Us=170 V，Uo=160 V，RL=25 Ω。图12 中vH1为变压器原边电压波形，vH2为变压器副边电压波形，iL为电感电流波形，io为输出电流波形。变换器工作周期为100 us，证明电路开关频率为10 kHz；变压器原副边均为三电平波形，证明变换器控制方式为DPS 控制；电感电流变化与之前理论推导结果一致，证明电路工作正常。将电路工作条件代入传输功率数学模型可得D2=0.193，观察试验波形结果可得D2=0.195，两者差值在误差范围内，验证了所建立数学模型的正确性。

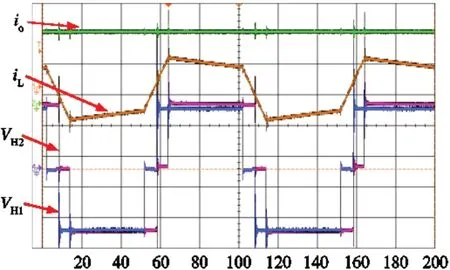
图12 DPS 控制对应的变流器工作波形

记录试验样机工作数据，能够得到试验样机效率曲线如图13 所示。在SPS 控制下，变换器最高工作效率为94.94%。 在DPS 控制下，试验样机具有最高96.08%的工作效率，在整个工作区间内效率均高于SPS 控制。试验结果验证了理论分析与仿真模型的正确性，DPS 控制能够有效提升变换器工作效率。

图13 变换器效率曲线

4 结 论

以DAB DC-DC 变换器为研究对象，分析了变换器工作原理，给出了SPS 与DPS 控制下变换器的数学模型。其次，建立了变换器在两种控制方法下的回流功率模型，并通过仿真模型验证了DPS 控制对变换器工作效率的提升。最后，通过基于SiC 的1 kW 试验样机对比试验，验证了文中理论分析的正确性。试验结果表明，相比传统SPS 控制方法，DPS 控制能够有效地提升变换器工作效率。