基于曲率半径及多传感器融合的动车组工况识别

张一喆，李 强

（1 中国铁道科学研究院集团有限公司 机车车辆研究所，北京100081；2 北京交通大学 载运工具先进制造与测控技术教育部重点实验室，北京100044）

高速动车组转向架构架、车体枕梁等结构分工况疲劳损伤研究的基础，是对动车组运用中所包含的曲线、道岔、桥梁、隧道等线路工况以及两车交会、风力风向、温度湿度等环境工况的准确划分和识别[1]。目前高速铁路的工况识别主要有基于图像信号处理和采用位移及力学传感器识别两大类思路。

图像识别技术起源于上世纪20 年代的航空航天领域[2]，上世纪90 年代后，被用于铁路领域。2006 年崔建荣、阮双琛等人在识别铁路线路时，利用图像灰像素与类内方差的变化率关系找到最佳的识别阈值[3]。2013年匡云帆在基于图像技术对线路特征分析的研究中，对道岔图像进行二值化处理，找到效果图的特征区域进行边缘提取，能较好地识别线路中的道岔工况[4]。文献[5]也提出一种通过图像检测轨道交点，较准确定位道岔所在区域的方法，为安全行车提供了保障。基于图像信号处理，进行运用工况识别，最大的优势是判别正确率高，并且对桥梁、涵洞以及线路周边环境的识别能力，是其他力学传感器不具备的。

但是，仅依靠图像进行工况识别，对数据存储空间和计算能力均有很高的要求，需要较大的硬件投入。并且，在获得结果的时效性方面，也不如基于力学及位移传感器的识别。笔者前期采用GPS 信号对CRH2A 型动车组工况进行识别，进而讨论了极端运用条件下枕梁的损伤状态[6]。并对CRH380AL 型动车组高速状态下部分工况进行识别，以此为据研究了该车典型工况下动车构架的应力状态[7]。另外，2017 年谢金鑫通过构架载荷以及部分应变测点的动应力数据，采用时频结合分析方法，对部分工况识别流程进行了研究[8]。同年，对于大量的工况识别特征参数，郭超提出了一种多视图的工况特征提取法，在识别中首次引入了分类集成算法，获得了良好的效果[9]。

在上述成果的基础上，对基于MEMS 陀螺仪、通过曲率所实现的工况识别进行了深入研究。在曲线和道岔曲率重合区，采用了GPS 及加速度信号的固有模态函数进行多传感器融合下的工况识别，效果较好，为下一步分工况的动车组损伤研究奠定了基础。

1 基于MEMS 陀螺仪的工况特征提取

1.1 MEMS 陀螺仪及各类传感器的安装

MEMS 陀螺仪利用科氏力原理，即旋转体中直线运动的质点因为惯性产生相对偏移这一现象，来计算瞬时角速度[10]。新型的MEMS 陀螺仪尺寸小、灵敏度高并且价格便宜，广泛应用于各领域的测试。

在以CRH380AL 动车组为例，进行工况识别研究时，将MEMS 陀螺仪以及GPS 等传感器安装在设备舱垂向支架上，具体位置如图1 所示。图中右下角胶带辅助固定的方块结构即为陀螺仪，GPS 通过扎带固定在其上部，GPS 上端是三向加速度计，该支架左侧吊装铁箱中安装有eDAQ 动态数据采集设备，可实时收集各类传感器信号。

1.2 工况特征提取实例

根据其工作原理可知，陀螺仪垂直于轨面的轴，即为动车组转向的敏感轴。现以该测试动车组某日在京广高铁某站进站停车并出站的过程为例，对陀螺仪敏感轴所采集数据的处理方法进行研究。

图1 陀螺仪等各类传感器及数据采集设备

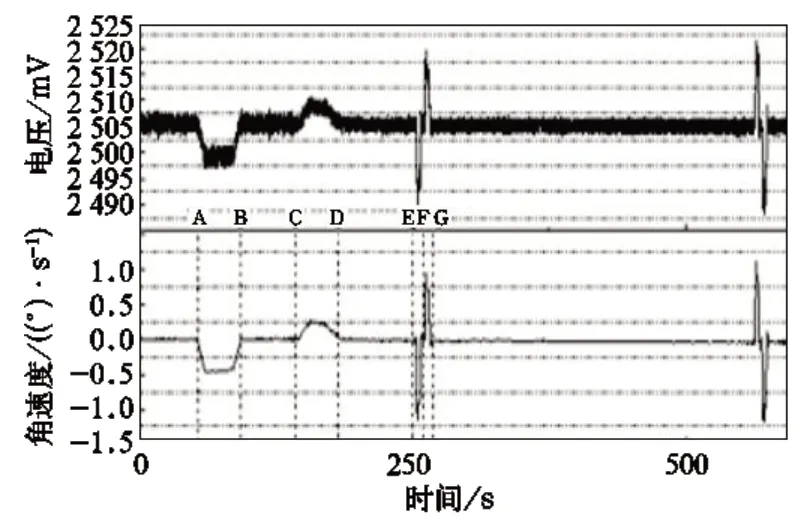
图2 敏感轴原始数据与处理数据对比

图2 中，上半部分为停站过程，敏感轴采得的原始数据。现结合动应力数据的处理方法，参照文献[11]去除零点漂移的理论，并采用8 层的db6 小波函数进行小波包去噪，最后代入该陀螺仪的敏感度系数如式（1）:

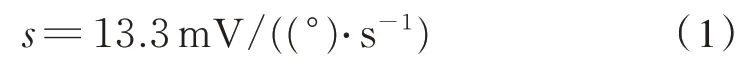
将电压值转换为角速度，得到如图2 下半部分的处理结果。

图中，A−B 和C−D 是两段梯形线为完整的通过曲线过程，其中两腰为缓和曲线，上底为圆曲线段。E−G 是曲率极小的一段“S”形曲线，结合当日的运行交路、并查询线路资料可知，该段曲线为侧向通过18 号道岔时获得的数据。

2 曲线和道岔工况判别及参数确定

2.1 曲线参数判定

基于曲率的工况识别中，曲率半径r，m 的计算方法由式（2）给出:

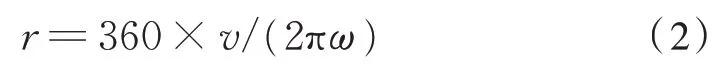
其中，v，m/s 是 GPS 的瞬时线速度，ω，(°)/s 是陀螺仪敏感轴的角速度。

根据v可得，通过各类曲线和道岔时，动车组实际的运行距离如式（3）:

同样，根据ω可知，动车组实际的转角为:

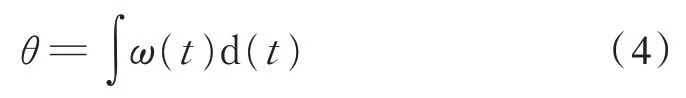
以图2 中C−D 段为例，通过式（2）、式（3）、式（4）得到该段曲线参数，并与实际参数对比见表1。

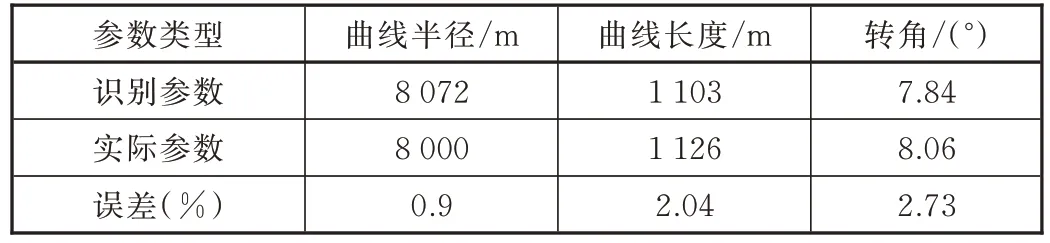
表1 曲线段识别参数与实际参数对比

表中看到，通过陀螺仪及GPS 信号获得的曲线参数与真实数据非常接近，识别效果良好。

2.2 道岔判定

每一种型号道岔均有与其相对应的道岔曲率半径、曲线长度及其转角。参照2.1 中的方法，对图2 中E−G段数据进行计算，将结果与18 号道岔实际参数进行对比，结果如表2。

表2 曲线段识别参数与18 号道岔实际参数对比

由表中的误差值可知，采用大量某一型号道岔的实测数据，给出基于曲率半径该型道岔的判别范围，理论上是可行的。

该测试车在正线运行时侧向通过的道岔中，12 号和18 号占97%以上。以18 号道岔为例，选取侧向通过时，24 组经过计算得到的道岔曲率半径数据如下:

采用W 检验法对上述数据做正态性分析，构造相关系数W如式（5）:

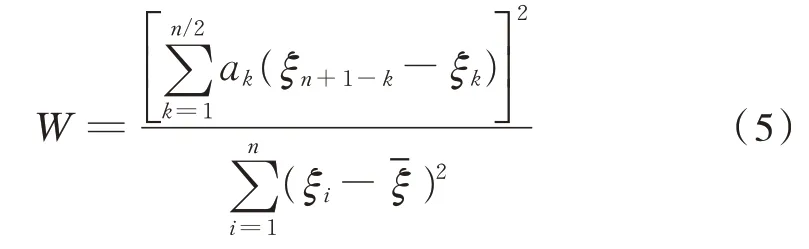
式中，n为被检验的样本容量，系数ak由文献[12]中a系数表给出。将样本按升序排列后，ξi为第i个样本，-ξ为样本均值。将半径数据代入式（5），得到系数W=0.960 9，大于文献[12]中的临界值，可以接受样本符合正态分布的假设。

采用极大似然法[13]进行分布拟合后，根据“3σ”原则给出两种型号道岔的判定区间如表3。

表3 基于曲率半径的道岔判定标准

3 识别效果分析

直线的曲率值是无穷大的，但由于测量误差和车辆振动等因素，导致极个别直线段曲率值在105数量级之上波动。按照线路设计规范，初步尝试将r≤20 000 m，作为曲线和道岔的识别范围。在该范围之内，凡是落入表3 判别区间的曲线，即判为道岔，其余为正常曲线段。现给出较为严苛的识别正确率计算方法如式（6）:

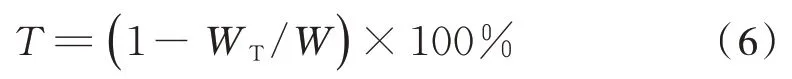
其中，WT为错误识别次数，等于误识别与漏识别之和；W为实际次数。

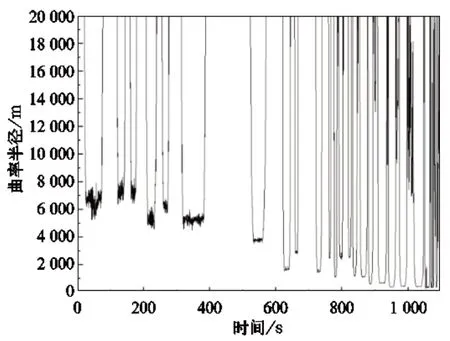
图3 250 km/h 级曲率半径-时间图

该测试车运用的交路中，主要包含250 km/h 和350 km/h 级客专线路。其中，350 km/h 级线路中仅有18 号道岔，并且最小曲率半径r≥5 500 m，依照式（6）得到对曲线和道岔的判别正确率均可达到97%以上。但是对同时含有12、18，以及个别9 号道岔的某些250 km/h 级客专，在小半径曲线的识别方面，正确率则非常低。

图3 给出某日测试车即将抵达柳州站的曲率半径−时间图像。图中，700 s 之前的9 条曲线均可以与实际线路对应，而在700 s 之后，由于曲线和道岔曲线半径范围重合，导致12 号和18 号道岔识别正确率分别为25%和66.7%，远不能满足应用要求。

4 多传感器融合的识别方案

4.1 固有模态函数的能量熵

希尔伯特−黄变换是上世纪末出现的处理时间序列的新方法。其中的经验模态分解(EMD)是将信号中，不同尺度的趋势和波动逐级分开，获得固有模态函数(IMF)。由于其分解过程的平稳性，使得各阶IMF 通常具有明确物理意义[14]。

前期大量试验发现，部分加速度信号的IMF，可能对某些振动特征有明确表达。研究各阶IMF 对不同类振动反应出的差异性，通常从其能量的差异入手。尝试给出IMF 能量熵的计算方法，参照下式信息熵的定义[15]，见式（7）:

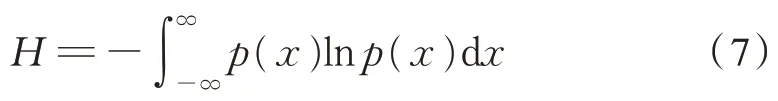
式中，p(x)为联合概率密度函数(x1，x2，...，xn)，则信息熵H是每个p(x)的函数，当所有概率值相等时，H取得最大值。

同理，将每级IMF 在时间轴等分N段，设第i段的能量为Wi，整段时间轴上的能量为W。将各段归一化，设qi=Wi/W，并根据式（7），给出IMF 的能量熵如下:

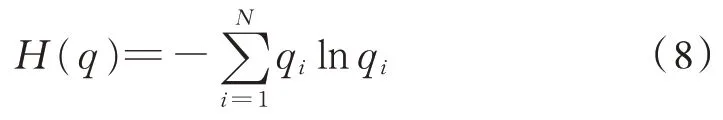
和信息熵类似，上式直接反应出IMF 各段能量分布的均匀程度。

4.2 不同工况的能量熵差异

为了区分曲率重合的曲线和道岔，先尝试对构架侧梁端部的垂向加速度信号进行8 阶EMD 并计算各阶IMF 的能量熵。

以图3 中的线路为例，选取120 s 的半径7 000 m 曲线、450 s 附近一段直线、1 030 s 半径 400 m 曲线以及1 070 s 附近一组12 号道岔的垂向加速度数据，按照文献[16]给出的建议，选择N=15，采用式（8）计算，得到每种工况下8 阶IMF 的能量熵见表4。

表4 中可以直观看出，自第4 阶开始，12 号道岔的能量熵明显大于其他3 种工况。

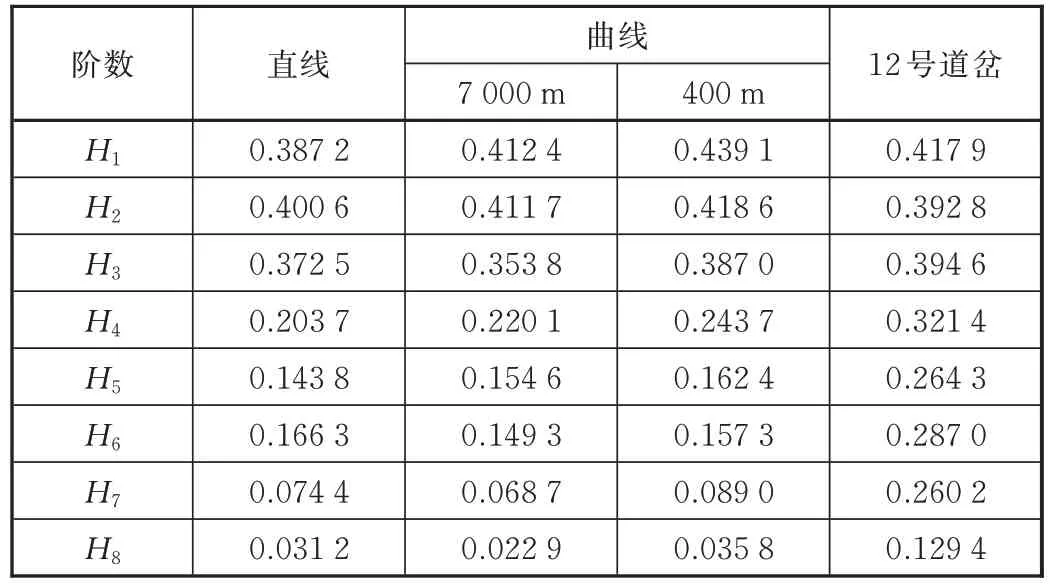
表4 各工况加速度信号IMF 能量熵

4.3 基于能量熵差异的道岔识别

基于上述分析，现将两类道岔各10 组数据8 阶能量熵的每阶均值作为母体，检验各10 组道岔曲线范围内的圆曲线各阶均值与母体的差异性。篇幅所限，仅在表5 中给出母体均值。

采用t检验法，构造变量t如式（9）:

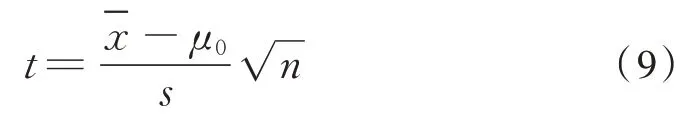
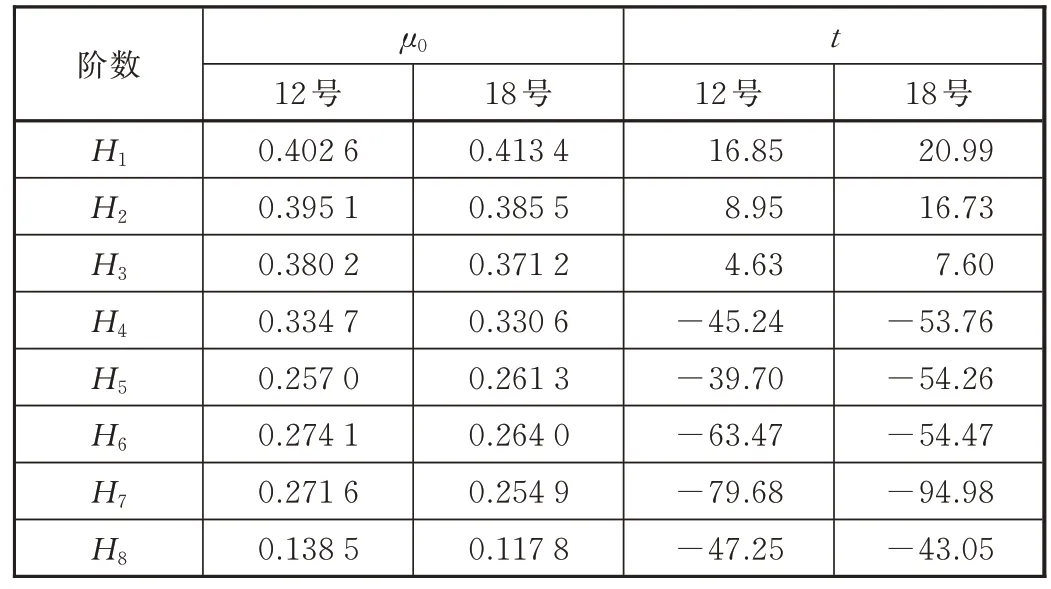
表5 母体IMF 能量熵及t 值

查t分布表，即便取显著度为1%时，所对应的自由度下tα=3.25，表中所有的t值均满足|t|＞tα。由此说明，同一半径范围内的曲线和道岔的各阶IMF 能量熵存在显著差异。

前几阶包含IMF 的高频部分，所以从表5 中可以看到，通过曲线与道岔时，构架振动特性的较大差异存在于低频部分，4～8 阶差异性明显更大。

选择4～8 阶IMF 能量熵值作为特征数据，定义指标函数如式（10）:

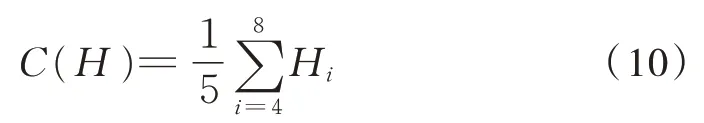
选择区分道岔和曲线的阈值，可借鉴支持向量机（SVM）思想，即寻找一个超平面，将两类数据分开，并使距离平面最近的数据尽可能远。

考察道岔及曲线的C(H)值，基于上述思想，给出裕度较大的阈值Ct=0.19。如此，对于道岔曲率范围内的曲线，均将其C(H)值与Ct进行比对，当C(H)≥Ct，判其为道岔，反之判为曲线。

5 结 论

在动车组结构分工况的损伤研究过程中发现，对线路工况的准确划分和识别，是疲劳损伤分析的基础。

在采用MEMS 陀螺仪及GPS 对曲线和道岔做基于曲率半径的识别和区分时发现，此方案仅能在350 km/h 速度级的线路上获得良好效果，而对于存在大量小半径曲线及12 号道岔的250 km/h 级线路，则无法有效识别。

根据以往大量构架加速度试验的经验和结论，尝试采用构架侧梁端部的垂向加速度信号对同曲率的道岔和曲线进行区分。首先依据信息熵的定义给出了各阶IMF 能量熵的计算方法，进一步发现各类工况间能量熵的差异特点，最终给出基于IMF 能量熵的曲线和道岔判别依据。

同样以图3 的数据为例，融入加速度信号的多传感器识别方案相对于仅基于曲率的识别，可使综合识别正确率由之前不足50%提高到了89.29%，能很好满足工程需要。