基于改进深度强化学习的三维环境路径规划

封 硕 舒 红 谢步庆

1(长安大学工程机械学院 陕西 西安 710064) 2(长安大学理学院 陕西 西安 710064)

0 引 言

路径规划是移动机器人导航的重要组成部分，目前大多研究成果显示在二维环境下的路径规划比较成熟，但是在三维环境下的路径规划比较薄弱。在三维环境下，会更容易碰到不平坦、多峰谷、多阻碍的地理环境状况，且不停地上下坡会带来更多能量损耗，所以需要找寻一条在最短的基础上，减少爬坡入坑(即减少耗能)的路径[1]。

蚁群算法是一种典型的三维路径规划方法，其信息素具备一定记忆功能是显著优点，但其缺点也很明显[2-3]。首先，它无法彻底解决三维环境路径规划问题，最终找寻的路径还会穿过山或者坑，不符合实际需求；其次，其算法收敛问题并没有得到很好的解决。基于层次包围盒碰撞检测的优化算法[4]是一种针对三维场景的路径规划问题的算法，虽然达到了路径优化的效果，且提高了时间效率，但没有对障碍物进行细化分析，对一些特定场景下的问题解释力有限。粒子群算法也是分析三维环境下的路径规划的传统算法[5]，且解决其三维环境路径规划有良好的结果，但是仍然存在陷入极值和没有较好的寻优效率问题。

深度Q学习算法(DQN)是结合了深度学习的感知能力和强化学习的决策能力的人工智能方法。感知能力和决策能力是衡量智能的大指标，强化学习的弱感知能力致使机器人难以直接通过学习高维状态输入去控制输出决策，而深度学习可用网络结构来映射Q表，从而解决Q-learning的维数灾难问题。近年来，研究表明在未创建地图情况下利用DQN实现移动机器人的导航是完全可行的，且利用DQN在栅格化地图中初步实现了路径规划，得到之前从未得到的较好结果[6]。但在该文献中，DQN算法收敛性较弱，没有对算法收敛性进行提高。文献[7]提出的改进DQN算法不仅解决了DQN算法存在严重的过估计问题，且将改进DQN应用于实际问题，取得良好结果。但是没有针对三维路径规划问题进行分析。最近，已经有越来越多学者使用深度强化学习算法解决各个行业的问题，且在路径优化问题上已经相对成熟[8-10]。理论上，将DQN应用在路径规划中优于其他算法，但需要解决三维环境的路径规划设计问题，使得与最优值差值较小的非最优值得到较大的缩小，与最优值差值较大的非最优值得到较小的缩小。本文利用神经网络进行建模，应用到深度Q网络中设计相应的改进算法，并将改进算法应用到三维路径规划的问题中。

1 改进深度强化学习算法

1.1 DQN深度强化学习

在机器学习方法中，深度神经网络具有感知复杂环境的能力，而强化学习是解决复杂决策问题的有效手段，因此Mnih等[11]将两者结合起来能够解决复杂环境的感知决策问题。本文针对三维路径规划的问题，基于DQN模型中深度学习的感知能力，结合强化学习的决策能力，即使用深度神经网络框架来拟合强化学习中的Q值，可以使机器人实现真正自主学习且提高找寻最优路径的效率，获得稳定的奖赏值。

DQN是一种结合了强化学习中的Q学习(Q-learning)和深度学习中的卷积神经网络(CNN)的算法。利用卷积神经网络实现了对Q表的建模，从而完整地表示所有的状态-动作值，Q-learning 通过马尔可夫决策[12]建立模型，核心为四元组：目前状态，动作，奖励和下一步状态。智能体根据当前环境的状态来采取动作，在获得相应的奖励后，能通过试错的方法再去改变动作，使得在接下来的环境下智能体能够做出更优的动作，得到更高的奖励。

DQN采用神经网络作为函数近似的模型，其参数需通过强化学习反复调整，达到神经网络对Q表建模的目的。深度强化学习能够将强化学习的决策能力和深度学习的感知能力相融合。首先通过深度学习对大规模原始输入数据进行简单但非线性的转换，得到该原始数据更高层次的抽象表达，从而得到数据内在的规律。然后结合强化学习，不断调整神经网络参数，使得神经网络能够更好地拟合Q表。最后智能体依据神经网络能够获得一个更为理想的策略。

深度Q网络依靠目标值网络Target Net(Q’)以及回放记忆单元D(Q空间)对神经网络的稳定性进行有效的提高，同时使用随机梯度下降函数更新在线值网络Main Net(Q)，使得深度Q网络对较为复杂的控制问题有一定的处理能力，而且深度Q网络在训练的过程中无须添加额外的数据信息，将原始数据直接输入一个卷积神经网络，从而使得智能体对数据的处理更接近人。然后使用强化学习中的Q-learning，通过与环境进行交互，得到带有奖赏值的样本数据，从而更新在线值网络的参数，经过固定的时间段，将在线值网络的参数复制到目标值网络，利用目标值网络计算目标值，在线值网络以及目标值网络的更新如图1所示。其中：s为智能体的当前状态；st+1为智能体的下一个状态；r为奖励；a为机器人的当前动作；at+1为机器人的下一个动作；γ为折扣因子；ω为主网络权值；ω-是目标网络权值。

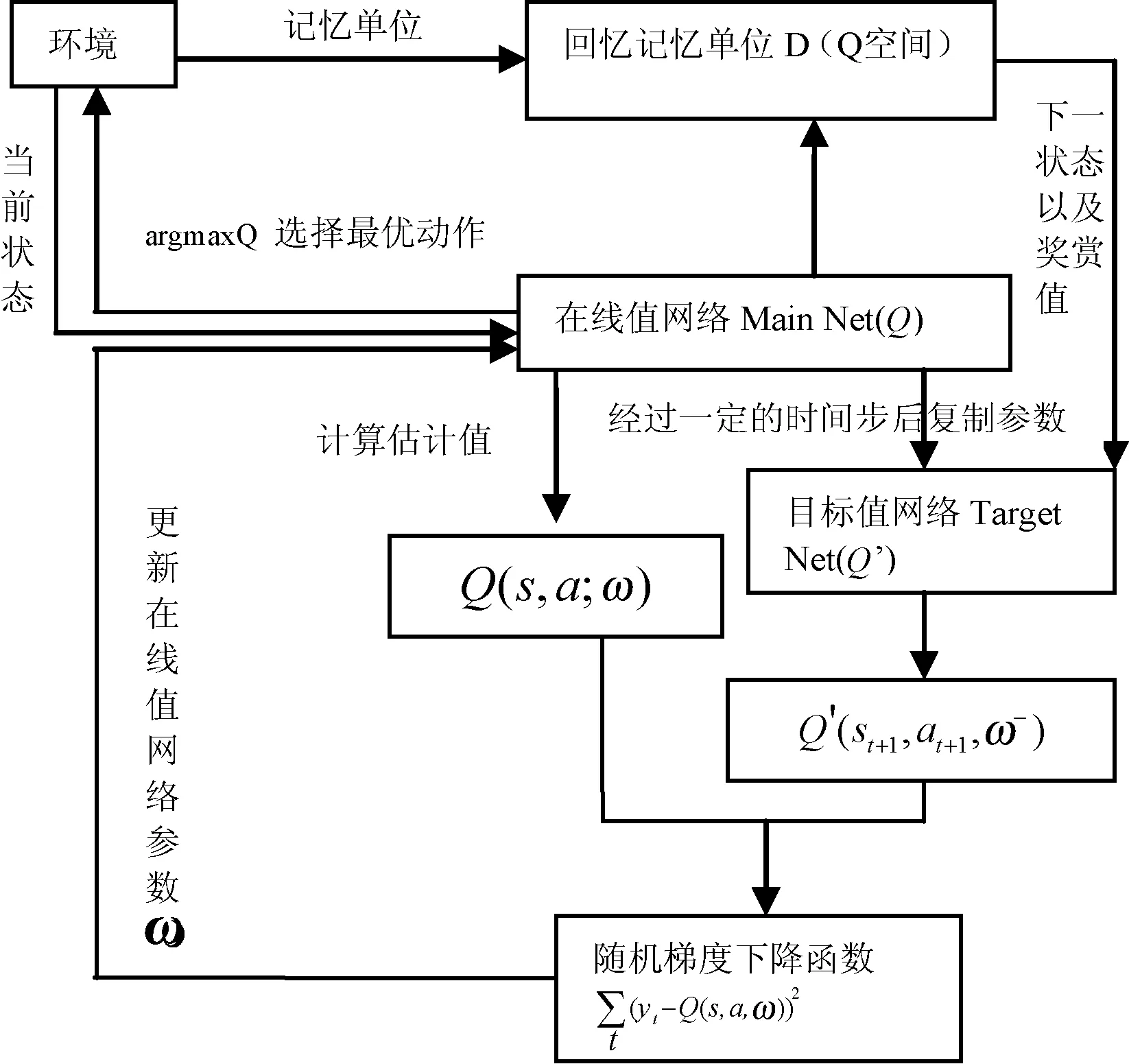
图1 DQN算法流程

状态值函数求取目标值即目标值函数为：

DQN通过误差更新网络的权值，误差评价函数为输出值和目标值的差的平方求期望，即：

Lt=E[(yt-Q(s,a,ω))2]

采用梯度下降法更新网络权值参数(▽为梯度符号)：

ωt+1=ωt+E[yt-Q(s,a,ω)]▽Q(s,a,ω)

更新参数ω-：由参数ω延迟更新获得，即在参数ω实时更新，经过若干轮迭代后，将当前Q网络的参数赋值给Q-target网络。

1.2 过估计问题

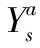
估计值与真实值在状态s下的误差Bs为：

γmaxa′Qtarget(s′,a′))=

γ(maxa′Qestimation(s′,a′)-maxa′Qtarget(s′,a′))=

maxa′Qtarget(s′,a′))=

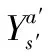
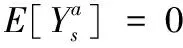
1.3 过估计问题的改善策略

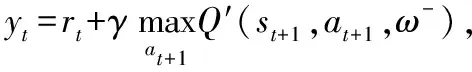
B(st,at,rt,st+1)=

计算目标值：yt=V*(s)×B(s,a)

1.4 算法步骤

(1) 初始化经验回放存储区D、Q网络ω、目标Q′其权值ω、ω-为随机值。

(2) 开始新一轮，生成环境、高峰、低谷、目标点。

(3) 通过神经网络(卷积神经网络)f(s,a,ω)≈Q*(s,a)输入目前状态S，输出当前状态S下动作ai(其中i=1,2,…,n)的Q值得到Q值向量[Q(s,a1),Q(s,a2),…,Q(s,an)]。

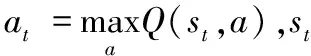
(5) 执行动作at，得到当前奖励rt，下一时刻状态st+1，将(st,at,rt,st+1)存入D，奖励函数为：

(6) 从D中随机采样一批数据，即一批(st,at,rt,st+1)四元组，计算变更函数(b<1)：

B(st,at,rt,st+1)=

计算目标值：yt=V*(s)×B(s,a)用Q-target网格计算目标值V*(s)，sT为最终状态：

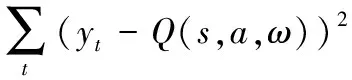
(7) 损失函数：

式中：Q(s,a,ω)为当前网络的输出，用来评估当前状态动作对的值函数；Q(st+1,at+1,ω-)为Q-target的输出，用来求得目标值函数的Q值。然后更新参数ω和ω-。

2 实 验

2.1 实验设计

为了验证NDQN的性能，本文在Python和MATLAB实验环境下对DQN和NDQN做对比实验。实验中的三维环境是积木型的，同时具有符合现实意义的高峰和低谷，与传统二维环境相比，其障碍物具有一定的可通过性，比如在智能体允许通过的高峰和低谷范围内，三维环境中是可通过的，且可详细计算需要消耗的能量与时间，三维环境更加符合现实意义的地理环境。

本文将初始化回忆记忆单位的大小设置为14 400，折扣因子初始化为0.9，更正函数的底数b初始化为0.9，以步长0.1减少到0.4，贪心算法中进行探索的概率ε随着步长的增长由1逐渐减少为0.1。寻找最优结果。双网络结构，分别是在线值网络和目标值网络。两个网络都是卷积神经网络，并且网络的结构都是一样的，仅权值不同，目标值网络的权值来自在线值网络的权值，周期设置为300步。

通过将MATLAB与Python紧密结合，运用到三维路径规划中，能够更加真实地反映现实环境中的路况，更好地诠释三维环境中的路径规划。图2为三维环境路径规划实现流程。

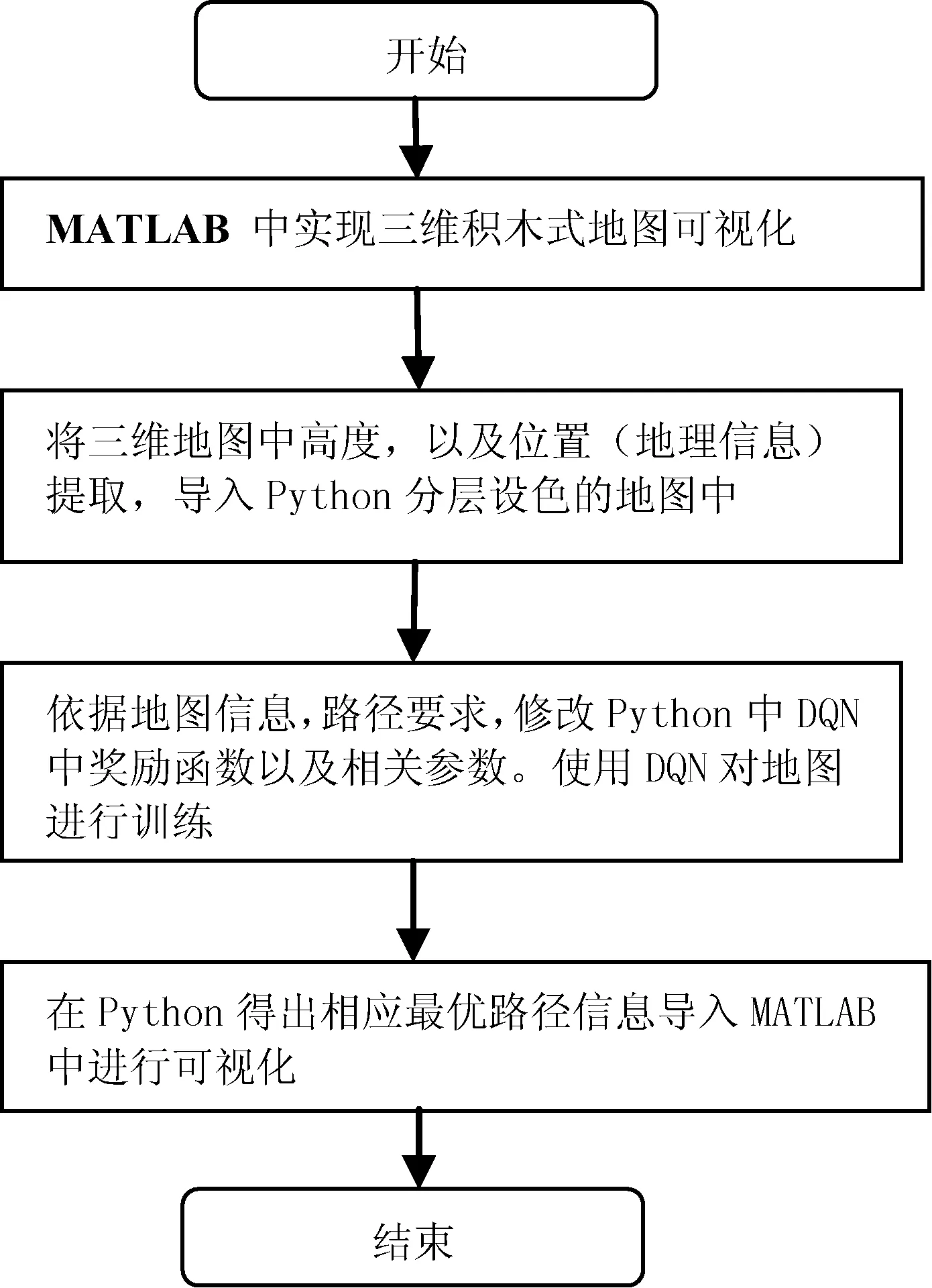
图2 实现三维环境路径规划流程

2.2 实验算例结果与分析

本文将NDQN和DQN应用在三维路径规划问题中，分别从平均奖励值、从起点到终点所需步骤数、误差分析图三个方面的收敛图对两种算法进行分析。平均奖励值越稳定，从起点到终点所需的平均步骤数越少，误差越小，说明算法的性能越好。因为神经网络是Q表的泛化模型，使深度Q网络存在不稳定问题，为了缓解不稳定问题，DQN采用双网络结构和记忆回放机制提高了稳定性。和之前相似，DQN和NDQN在三维环境下，在路径、所需步数，以及奖励函数值的收敛图上进行对比。

图3为将深度神经网络应用于三维路径规划中所得的路线图。两种算法都得从起点至终点路径完全避开高峰或者低谷，取得满足实际情况的较优越的路线。说明在复杂的三维环境中，深度神经网络没有维数灾难的问题，且能够让机器人得到良好的路径规划。黑色方块为NDQN的实验路线，灰白色方块为DQN的实验路线。经过实验，NDQN与DQN所得的路线具有一定区别。虽然DQN也找到一条良好的路线，但其时而会经过半坡的地方，且不是最优路线，会陷入在低谷旁边徘徊的情况。NDQN图中的路线较DQN弯路少，且没有爬坡情况出现。因此，上述针对过估计问题的改善策略，NDQN得到的最优路线优于DQN。

图3 DQN和NDQN的最优路线图

如图4和图5所示，通过平均奖赏值分析算法的性能。以往的研究中平均奖赏值越高，算法性能越优越，而在此三维环境下的路径规划，由于给予没有坡度、没有坑的地方的奖励值为7，平均奖励值越高，并不一定是算法越优越，而很大可能是选择的路径不是最优路径。所以在三维环境下的路径规划，应分析平均奖赏值的收敛性以及稳定性。由图4-图5可以看出，NDQN在三维路径规划上取得了比DQN更稳定的平均奖赏值，且NDQN在1 000代左右就找到稳定的较高的平均奖赏值。在不同起终点变化的场景下，计算总共120次DQN和NDQN的平均奖赏值再求平均之后得到：NDQN比DQN收敛速度快大约60%。这说明上述针对过估计问题的改善策略，NDQN得到的平均奖赏值更稳定。

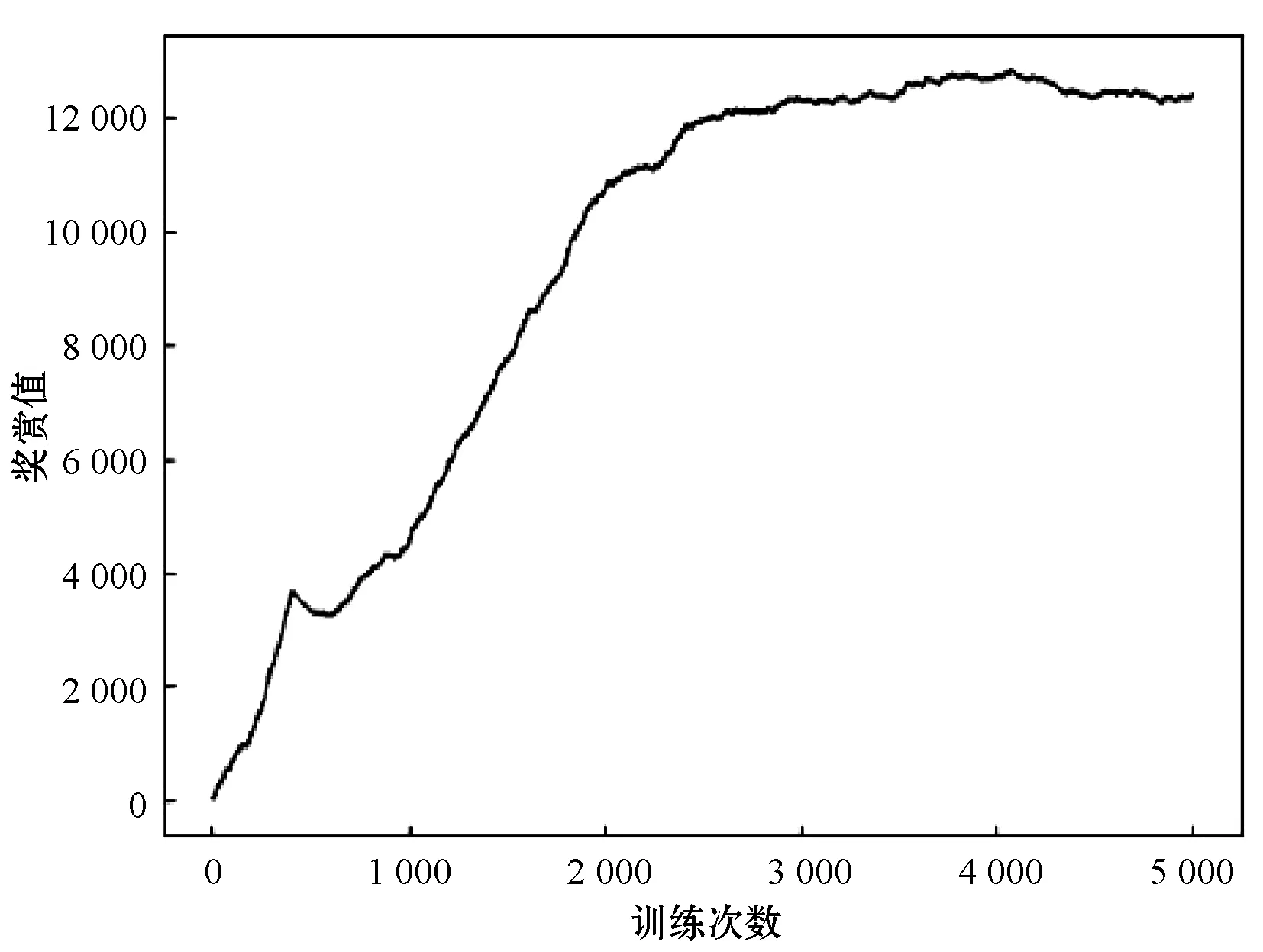
图4 DQN奖赏值收敛图

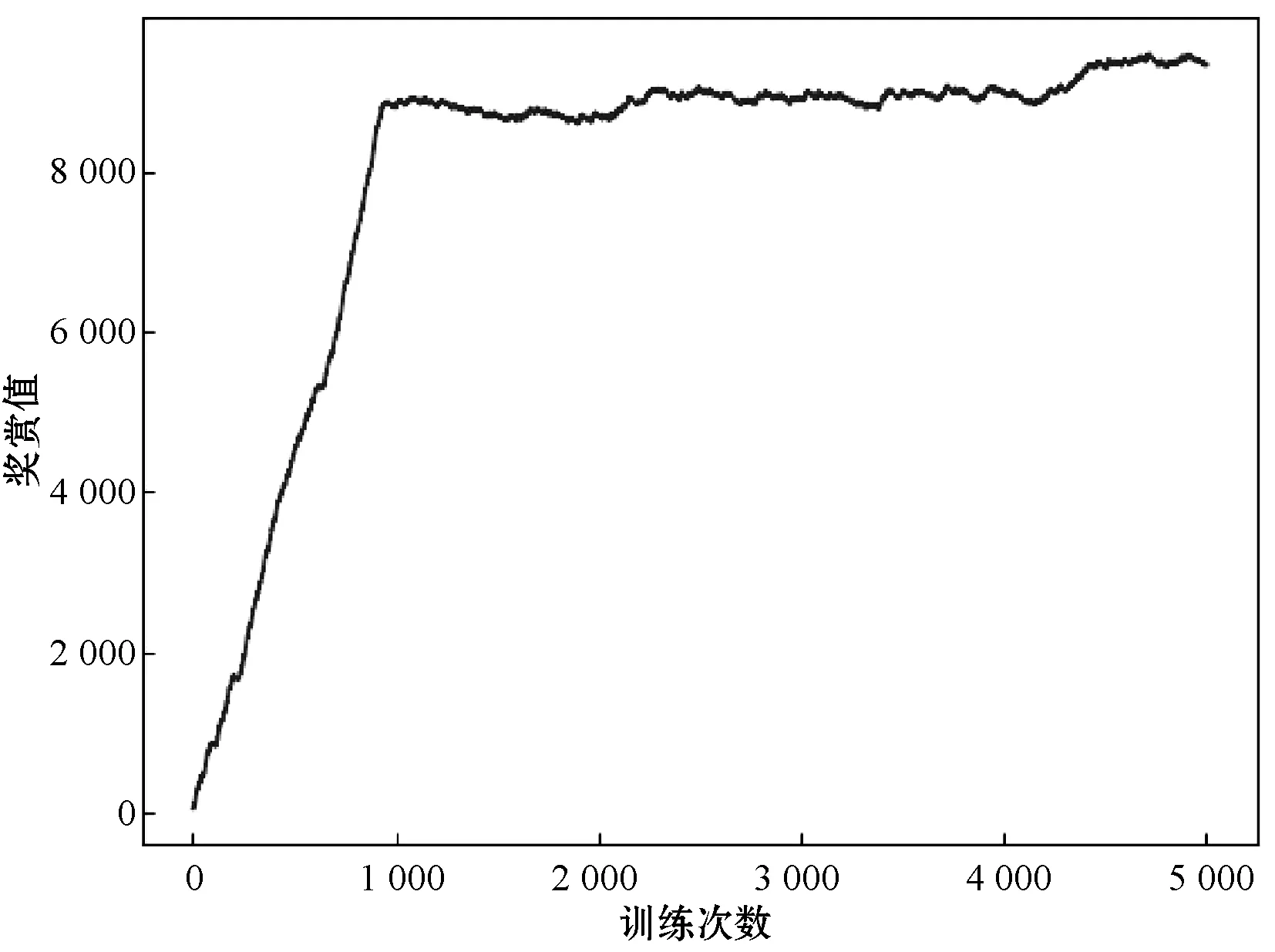
图5 NDQN奖赏值收敛图

如图6和图7所示，通过误差分析算法的性能。和以往分析相同，误差越小，算法性能越优越。可以很明显看出，相对于DQN，NDQN的收敛速度变化不明显。但是，NDQN收敛时损失函数的值比DQN低了21%左右。说明上述针对过估计问题的改善策略，在不同起终点变化的场景下，NDQN得到的损失函数值降低。同时计算总共120次DQN和NDQN的损失函数值再求平均之后得到：NDQN得到的损失函数值减少21%。

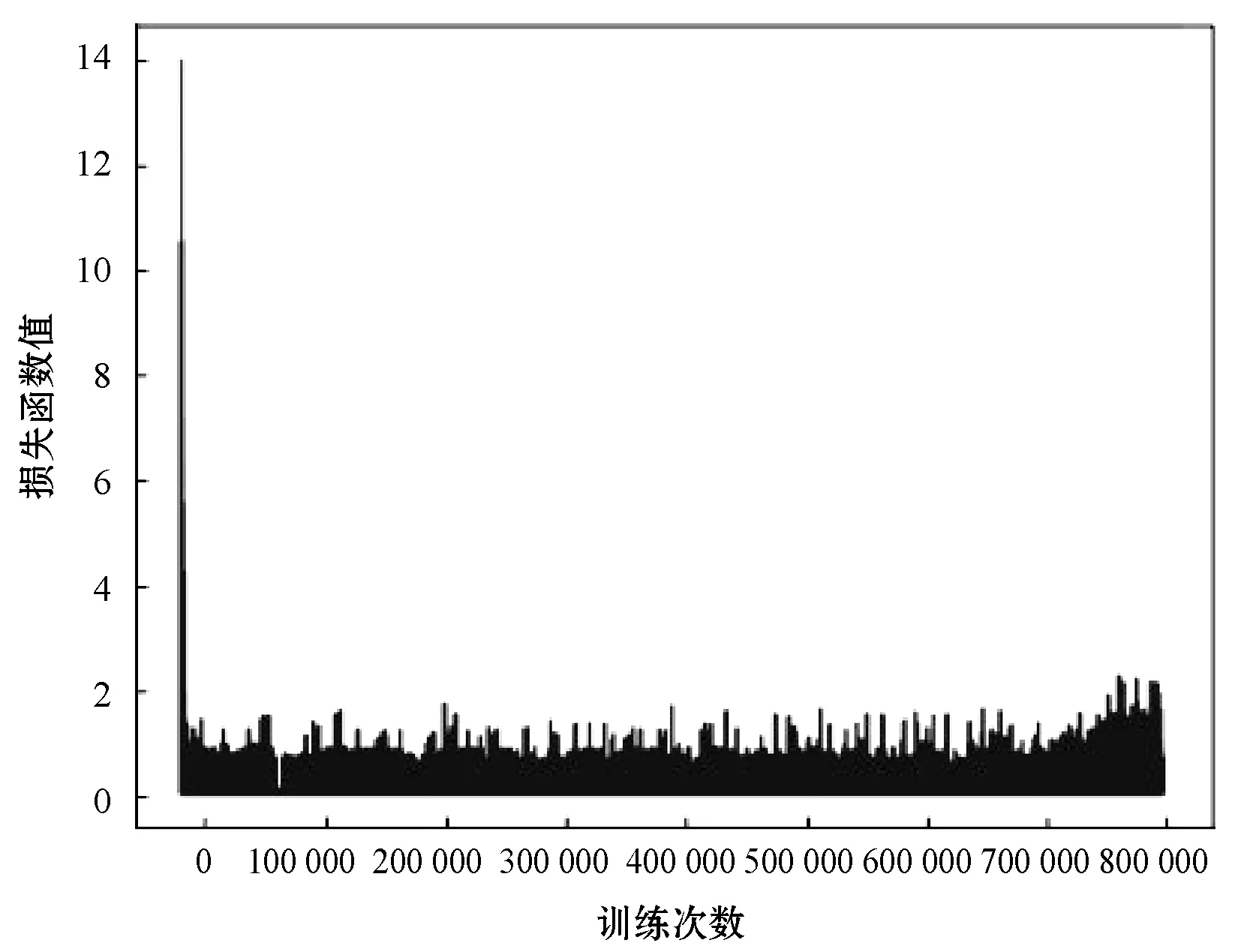
图6 DQN损失函数值收敛图

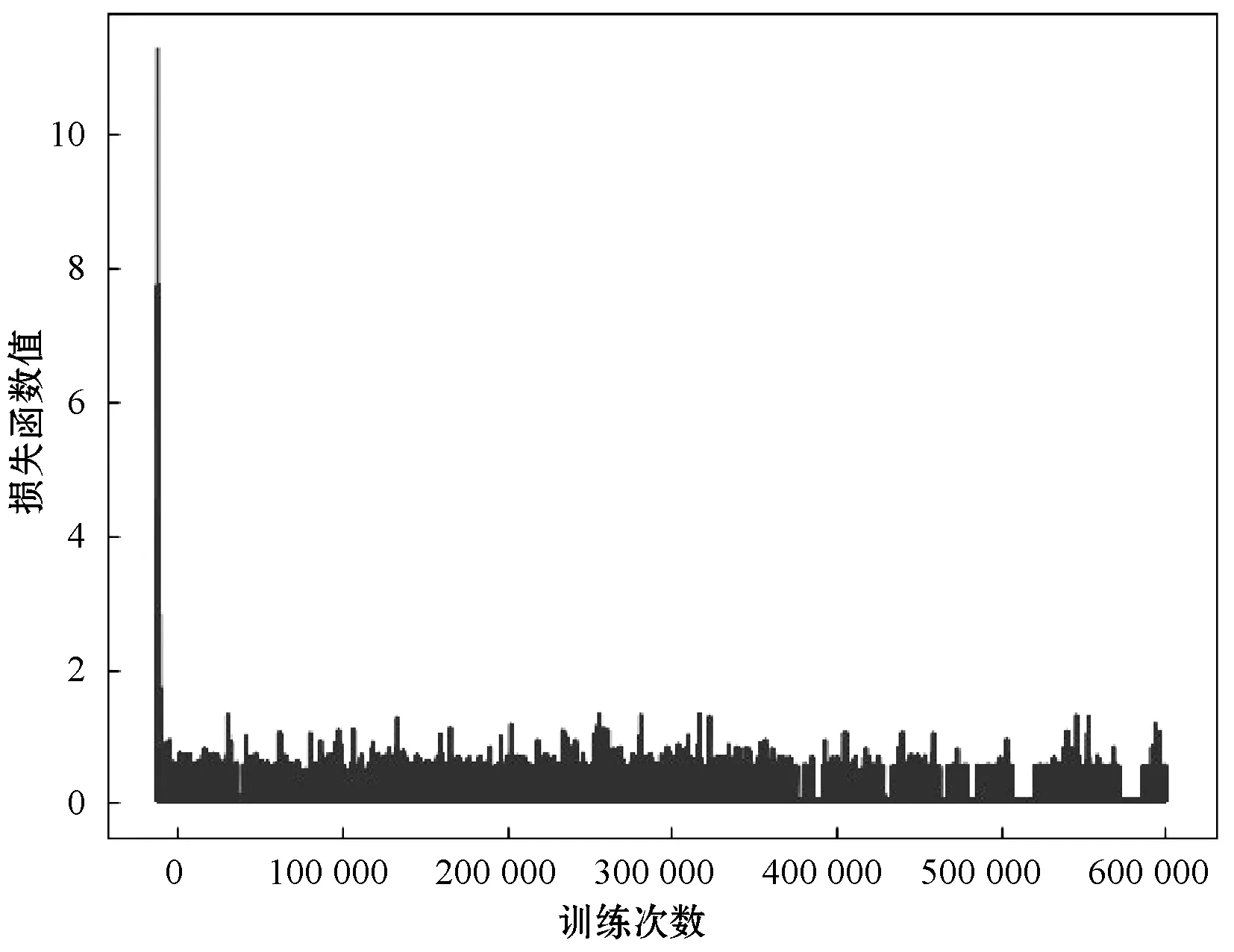
图7 NDQN损失函数值收敛图

如图8和图9所示，通过误差分析算法的性能。和以往分析相同，从起点到终点所需的平均步骤数越低，算法性能越优越。可以很明显看出，NDQN相比DQN有着更好的稳定性，而且震荡的幅度比较低，所需的平均步骤数降低了大约25%。这说明上述针对过估计问题的改善策略，在不同起终点变化的场景下，NDQN得到的平均步骤数量降低。同时计算总共120次DQN和NDQN的损失函数值再求平均之后得到：NDQN得到的平均步骤数量降低25%。

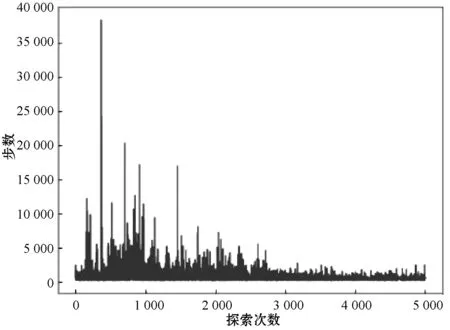
图8 DQN所需步数收敛图

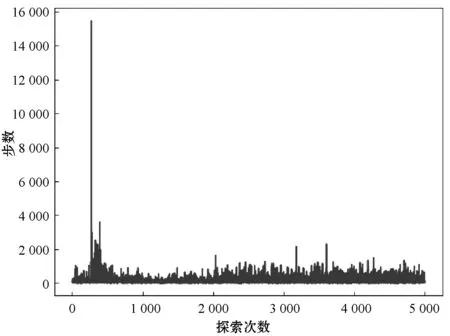
图9 NDQN所需步数收敛图

3 结 语

本文针对三维环境的路径规划问题，提出改进深度强化学习算法。算法中加入了差值增长概念，使得与最优值相差越近的非最优值变化得较大，反之，与最优值相差越远的非最优值变化得较小。实验结果显示：

(1) 改进的算法 NDQN在三维环境中得到的路径明显优于DQN得到的路径，且在平均奖赏值、算法的稳定性、收敛性上都比DQN有一定程度的提高。

(2) 本文提出的更正函数应用在深度Q网络中可以有效地缓解深度Q网络存在的过估计问题。

总之，NDQN方法可以在更少迭代次数内得到更稳定的累积奖赏值，从而使得智能体可以在最短时间内获得最优路径。