抗差卡尔曼滤波及其在超短基线水下定位中的应用

罗才智，杨 鲲，辛明真，卫进进，张 凯，阳凡林*

（1. 山东科技大学 测绘科学与工程学院，山东 青岛 266590；2. 交通运输部天津水运工程科学研究所，天津 300456）

水下目标定位导航是海洋开发活动与海洋技术发展的基础，水下声学定位系统包括长基线（Long Baseline，LBL）定位系统、短基线（Short Baseline，SBL）定位系统、超短基线（Ultra-Short Baseline，USBL）定位系统和GNSS智能浮标（GNSS Intelligent Buoys，GIB）系统[1-3]。其中，USBL 定位系统利用各基元信号间的相位差来解算目标的方位和距离，实现对目标的跟踪定位[4]。相较于其他几种水下定位方法，USBL 定位系统由于只需要一个换能器，因此其集成系统价格更低廉，且有构成简单、操作维护方便的优点[5]。

受海洋环境动态变化、测量仪器安装校准偏差、外围设备测量可靠性、声速测量与改正精度等因素的影响，USBL 定位会出现较大粗差和连续异常误差。经典卡尔曼滤波的前提假设是滤波的状态模型和观测模型准确，且状态噪声和观测噪声均为互不相关的零均值高斯白噪声[6]，因此经典卡尔曼滤波无法有效消除USBL 定位数据中的较大粗差。抗差卡尔曼滤波作为经典卡尔曼滤波的一种改进方法，是通过调整观测噪声协方差阵提高滤波的抗差性，因而更适于消除实际动态定位中的连续误差。

此前，对于面向不同实际工程应用的粗差数据处理，相关学者提出了多种抗差滤波方法。王润英等[7]提出基于M 估计的抗差卡尔曼滤波算法，利用抗差估计方法识别粗差并修正其观测方差，通过IGG3 等价权函数构造等价权来减弱参数估计中异常值的作用，从而减弱变形监测中粗差对参数解的影响。李雅梅等[8]针对移动机器人定位的测量误差和位姿误差问题，引入多新息向量来提高非线性系统的精度，并利用Huber 权函数改变测量值的权重，引入自适应因子调整状态协方差矩阵大小，从而实现对测量更新估计值的精确估计。黄珏等[9]提出一种集中式非线性抗差卡尔曼滤波算法，通过设计代价函数重构系统测量噪声方差，并利用UKF 处理非线性观测方程，解决了传感器测量异常、数据传输错误和融合数据异常的目标跟踪问题。彭月[10]以卡尔曼滤波中目标位置参数的预测状态不符值的标准化残差作为抗差判断量，自适应地判断当前运动模型的准确程度，解决了目标导航定位中经典卡尔曼滤波结果易受运动模型误差影响的问题。Zhang Kai 等[11]为了解决反向散射数据异常而难以获得K 分布参数稳健估计解的问题，提出一种基于稳健统计的K 分布参数估计算法，将DI 统计量替换为鲁棒统计量，以无异常情况下的效率损失为代价，提高MoM 方法的鲁棒性；以增加计算时间为代价，自适应裁剪异常值，提高计算效率。在存在异常值时，应用鲁棒统计和自适应微调算法，可获得更精确、稳健的估计解。

尽管针对抗差卡尔曼滤波的理论研究日益深入，当面向不同的实际工程应用时，受测量误差类型、观测模型等影响，仍须结合实际情况对滤波参数进行调整。本文主要面向抗差卡尔曼滤波在USBL 定位数据处理中的应用，针对定位中的数据扰动，选择目前国际上经典的Huber、IGG1、IGG3 等价权函数，通过调整更新后状态向量估计值中观测噪声的协方差矩阵，重点对比分析不同等价权函数对USBL 定位数据的抗差滤波效果，为水下定位的实际应用提供参考。

1 USBL 定位原理

USBL 定位系统是通过测量应答器与声基阵中各声单元的相位差来确定应答器到声基阵的方位，并测量应答器到声基阵之间的距离来确定目标位置的一种定位技术[12-13]。USBL 的声基阵至少需要3 个声单元，并构成声单元坐标系，如图1 所示。假设3 个声单元位于2 个相互垂直的基线上（x 和y 轴上），各方向上基元间距（基线）均为d，应答器发出的信号到基阵原点的声线与x 轴及y 轴的夹角分别为θmx, θmy[14]。

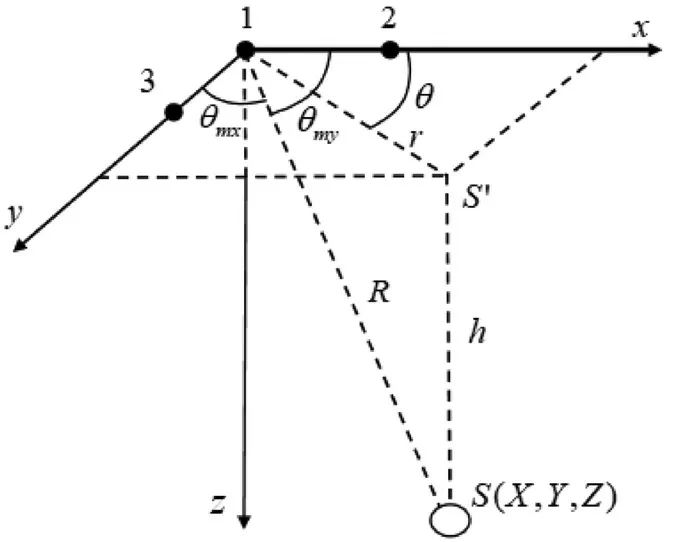
图1 USBL 定位示意图

通过测量往返时间和声速，计算得到斜距R为：

式中：c 为声波在水中的速度；T 为往返时间。

根据空间几何关系可得

式中：θm为声线与声单元坐标系各坐标轴之间的夹角；λ 为波长；为相位差。

两声单元接收信号的相位差与信号入射角的关系可表示为：

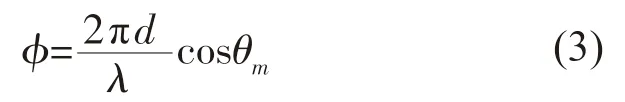
应答器S 在声单元坐标系位置可以表示为：

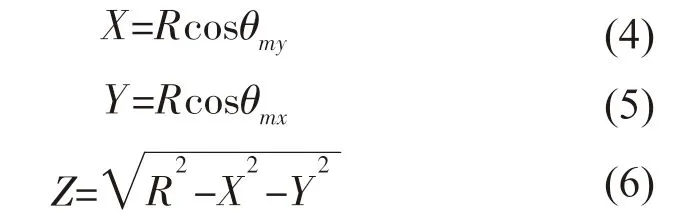
结合公式（3）可进一步表示为

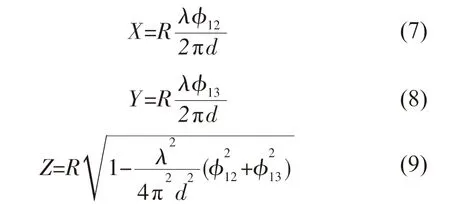
2 抗差卡尔曼滤波的USBL 定位

在经典卡尔曼滤波中，观测噪声通常假设为系统误差、功率谱密度分布均匀的白噪声以及随机的高斯—马尔可夫过程，且误差表现出随机性和独立性。但在实际观测过程中，观测噪声并不表现为随机分布，其功率频谱密度也并不一定为常数，数据中存在连续且大的粗差，在这些情况下，经典的卡尔曼滤波不能够很好的消除和调整连续粗差带来的连续数据波动问题，从而会导致滤波结果出现大的偏离。

当数据中出现偏离较大的连续粗差时，抗差卡尔曼滤波可以通过调整观测噪声的协方差矩阵，利用观测协方差矩阵代替原来的观测噪声协方差矩阵，来削弱粗差对滤波整体的影响。

对于超短基线定位的离散时间卡尔曼滤波，其状态方程及观测方程可以表示为

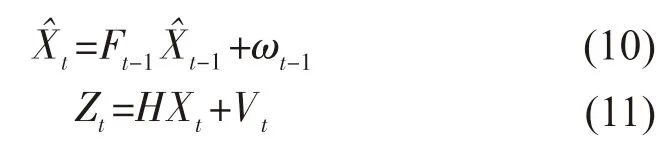
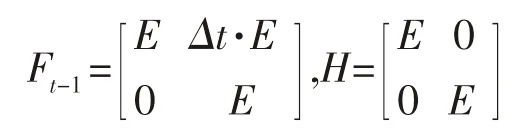
抗差卡尔曼滤波的估计准则为：

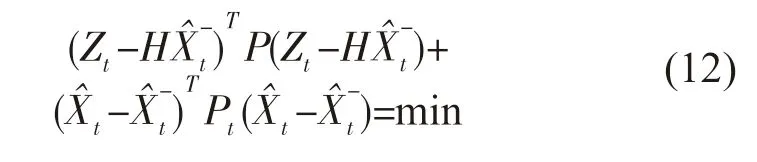
式中：P 为观测向量Zt的权矩阵，即观测噪声协方差矩阵的逆矩阵，取值6 阶单位矩阵；Pt为预测状态估计向量的权矩阵，即系统噪声协方差矩阵的逆矩阵，取值系数为10的6阶单位矩阵。

对上式求极值得到[16]：

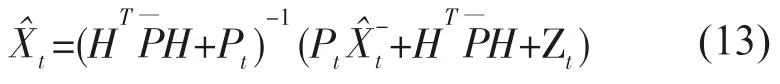
观测噪声协方差矩阵等价替换后得到的等价卡尔曼增益矩阵为

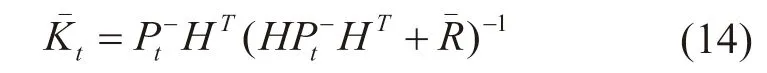
即状态更新方程可以等价替换为：

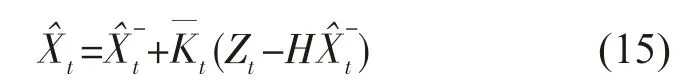
最后，更新系统噪声协方差矩阵为：

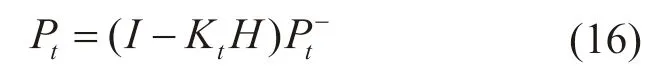
式中：Pt为更新后的系统噪声协方差矩阵；I为单位矩阵。

3 抗差卡尔曼滤波的USBL 定位

抗差卡尔曼对于数据的滤波处理重点在于对等价权的选择使用上，不同的等价权函数会产生不同的等价观测协方差矩阵，对于粗差的滤波效果也不同。考虑到抗差卡尔曼滤波能够满足对USBL 数据的抗差性和有效性的要求，选取目前实际应用中常见的Huber、IGG1、IGG3 三种等价权函数，它们的共同特点是利用观测值残差与残差的标准差的关系，求取标准化残差，并以经验获得的临界值界定观测值权值。对三种等价权函数的介绍如下：

（1）Huber 权函数

Huber 权函数划分为两段，包含正常域和可疑域，正常域的观测值仍采用原始权，其它的观测值则一律降权，显然该权函数缺少淘汰段，可能会减弱估值的抗差能力。

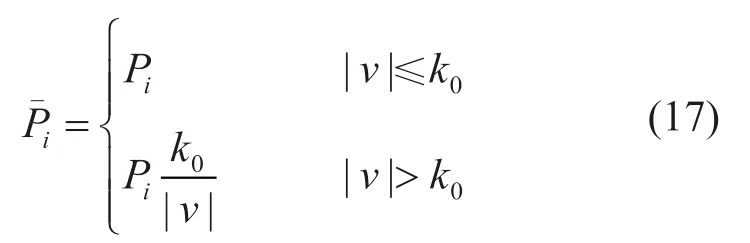
式中：v 为标准化残差[6]；k0取值1.0～2.0。

（2）IGG 系列权函数

IGG 系列权函数[17]主要基于测量误差的有界性提出的，选取标准化残差作为误差判别统计量[18]将其分为正常段、可疑段和淘汰段，分别对处于三种情况的观测值进行维持正常值、降权处理和淘汰处理。当观测值处于粗差较多的情况下，该方法较为有效[7]。

1）IGG1 权函数

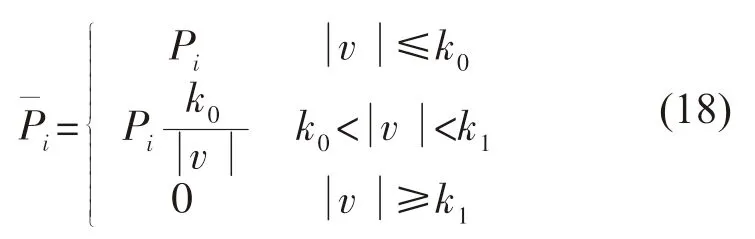
式中：k0一般取1.0～1.5；k1一般取3.0～4.5[18]。

可以看出，IGG1 权函数沿用了Huber 权函数在可疑域的降权方法，只是增加了淘汰域。

2）IGG3 权函数

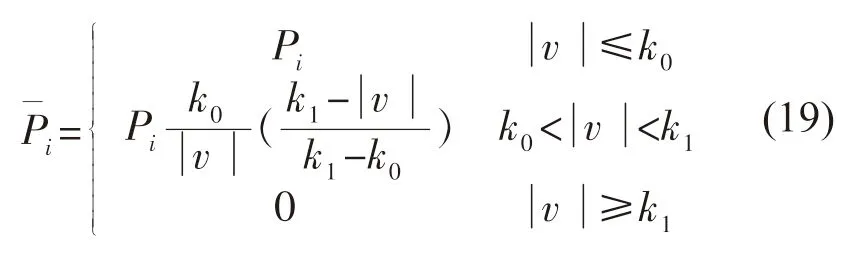
式中：k0，k1取值同上。

可见，IGG3 权函数是在IGG1 权函数的基础上改进了降权方法。

4 实测实验与分析

超短基线实际测量过程中，由于受测量环境、信号反射等因素影响，经常会出现较大粗差，对于测量数据整体精度会有很大影响。为了对比分析不同等价权函数对USBL 定位实测数据的粗差滤波效果，采用在中国南海为水下Swif 01 型ROV定位的USBL 实测数据作为实验数据，实验设备主要包括英国Sonardyne 公司的Ranger 2 USBL 定位系统、Syrinx 多普勒速度计程仪、英国SubSea7公司的Veripos LD4 接收机、法国Ixsea 公司的Octans 3000 型光纤罗经及运动传感器等，实验设备安装工作流程见图2。其中，测量船位置、超短基线换能器位置由星站差分GPS 接收机提供，利用USBL 测量的位置数据结合DVL、光纤罗经确定的速度信息，来精确推算水下ROV 的准确位置。

选取抗差卡尔曼滤波中的Huber 函数、IGG系列权函数作为求取等价权的方法，分析这几种等价权函数的抗差性，并与经典卡尔曼滤波进行对比，观察其抗差效果。图3～图5 分别为X,Y,Z方向各滤波方法的结果对比。

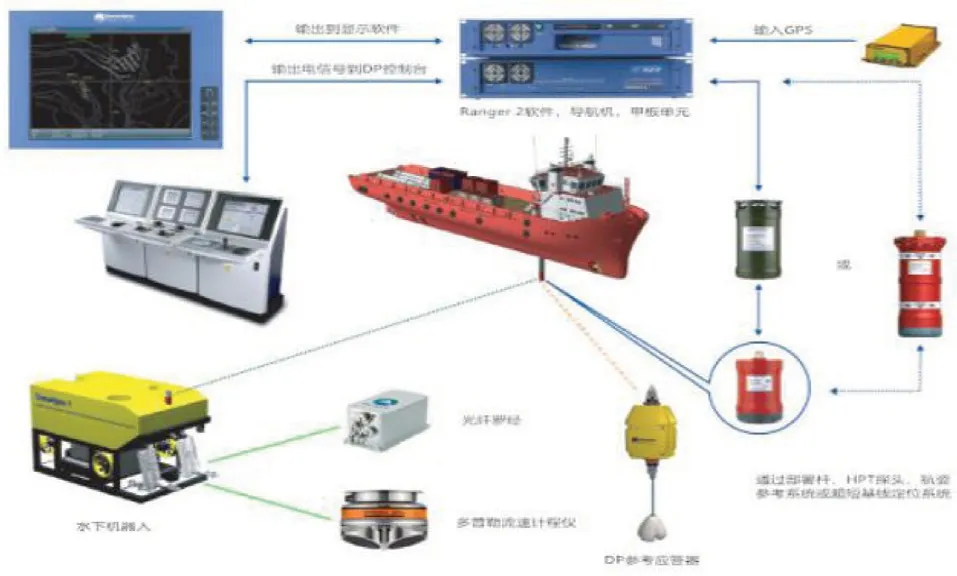
图2 实验设备工作流程

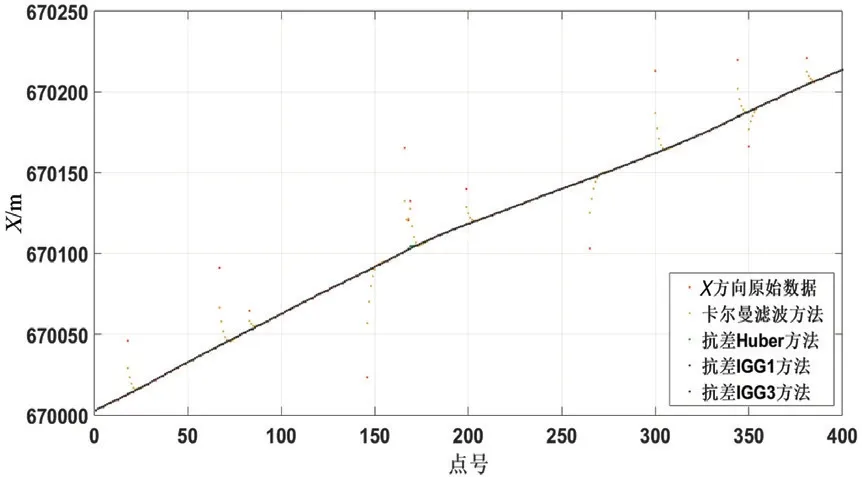
图3 X 方向的滤波结果对比

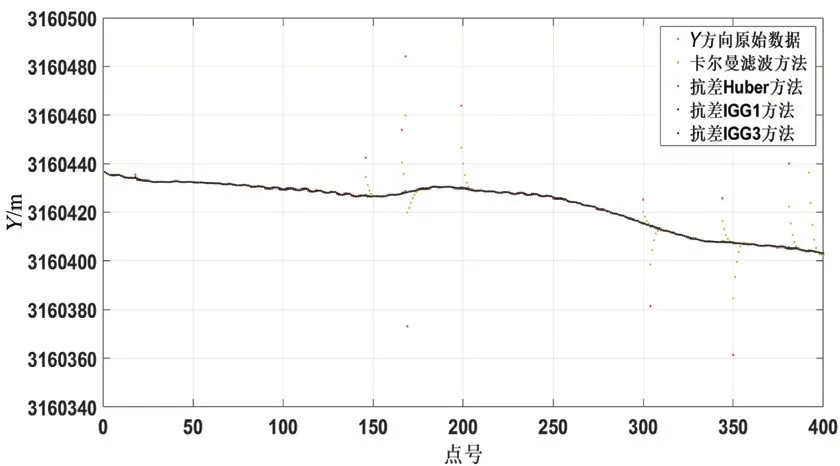
图4 Y 方向的滤波结果对比

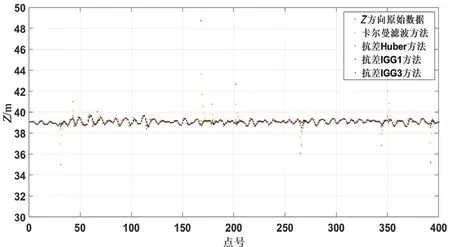
图5 Z 方向的滤波结果对比

通过图3～图5 各滤波方法结果对比图可以发现，实际测量中的某些较大粗差，经典卡尔曼滤波可以削弱，但不能有效剔除；对于抗差Huber 方法，其削弱程度略逊于抗差IGG 系列方法。由于实测数据仅能对各种等价权函数的抗差滤波效果进行定性分析，因此，设计仿真实验展开定量分析。

5 仿真实验与分析

将经过精细处理后的USBL 实测数据作为标准值，在此基础上，随机增加121 个异常值模拟粗差，其中根据实际工程情况模拟了一段由30 个异常值组成的连续粗差。模拟粗差的位置和大小见图6。图7～图9 分别为X,Y,Z方向上各方法的滤波结果对比曲线。

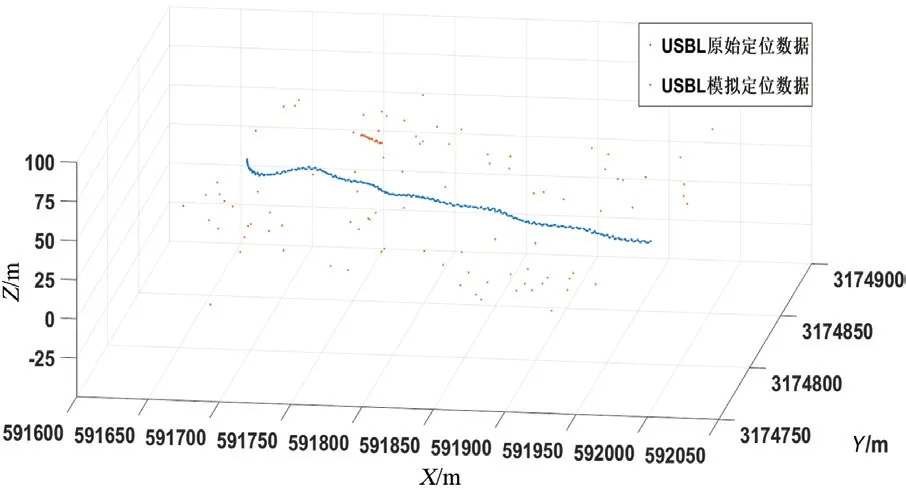
图6 原始及模拟定位数据

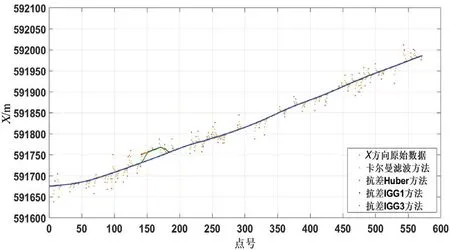
图7 X 方向的滤波结果

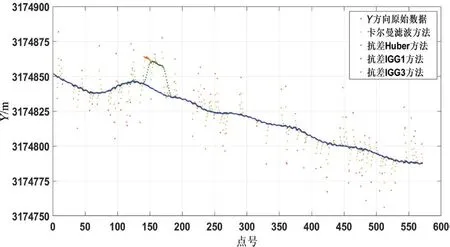
图8 Y 方向的滤波结果

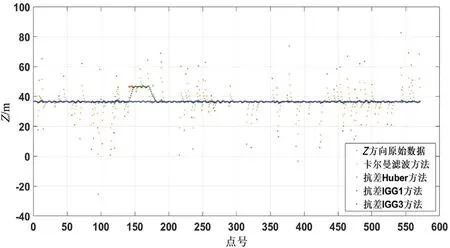
图9 Z 方向的滤波结果

为衡量滤波值与USBL 实测数据标准值之间的偏差，统计了各方法在不同方向上的RMSE结果，见表1。

根据上述各个方法计算得到的粗差结果，以0.5 m 作为判别X,Y,Z方向粗差剔除的阈值，并计算各个方法对X,Y,Z三个方向的粗差剔除率，各方法的粗差剔除率，见表2。

对实验结果分析可知：

（1）由图7 ～图9 可见，经典卡尔曼滤波方法只能够实现小部分的粗差剔除，对较大粗差处的滤波不彻底，连续粗差处的滤波结果较滤波前变化不大；抗差Huber 方法对于随机不连续粗差的剔除效果明显优于经典卡尔曼滤波，但对于连续粗差没有较大改善，且总体精度明显低于抗差IGG 系列方法；抗差IGG 系列方法明显消除了不连续粗差和连续粗差对USBL数据的影响，且两者效果相似。

表1 各方法滤波RMSE 结果

表2 各方法粗差剔除率

（2）由表1 分析，三种抗差卡尔曼滤波方法较真值的偏差明显小于经典卡尔曼滤波方法，采用经典卡尔曼滤波处理后的USBL 数据仍存在较大粗差。抗差Huber 方法在各方向上的RMSE 值总体有所改善但仍偏高，相比之下，抗差IGG 系列方法优于抗差Huber 方法，RMSE 值均可控制在0.3 m 以内。

（3）由表2 分析，经典卡尔曼滤波对各方向误差剔除效果较差，对粗差的改善效果不理想；结合图7 ～图9 可知，抗差Huber 方法在各方向上仅能剔除不到一半的粗差，且大部分未被剔除的粗差存在于连续粗差段处；相比前两种方法，将误差分为三段式处理的抗差IGG 系列在各方向上的粗差剔除率较高，均超过80%，总体剔除效果明显。

6 结 论

本文主要利用抗差卡尔曼滤波对USBL 定位数据进行滤波处理，对比Huber、IGG1 和IGG3等价权函数的抗差卡尔曼滤波结果，并分析经典卡尔曼对实测数据中的连续粗差的剔除效果。相比经典卡尔曼滤波、Huber 等价权函数的抗差卡尔曼滤波方法，利用IGG 系列权函数将误差分为3 段，分别采取不同抗差处理的方法，对USBL数据中的离散及连续粗差剔除效果较好，在一定剔除阈值下，该方法能够实现各方向80%以上的粗差剔除率，对实际USBL 定位数据的拟合处理具有一定参考价值。