两相流作用下缓波形立管的动力响应研究*

顾继俊 李云龙

(中国石油大学(北京))

0 引 言

在深水油气田勘探开发中，深水立管是必不可少的水下设备[1]。例如常见的钢制悬链线立管(SCR)可应用在水深3 000 m左右的海况中，但因其为钢制，导致立管触地区域(TDP)弯曲刚度非常大[2]，容易产生疲劳损伤。为了解决钢制悬链线立管在深水中存在的问题，一种深水缓波形立管(LWR)以其更好的顺应性得到广泛应用。其原理是在立管上安装质量较轻的浮筒，利用浮力使立管的一段隆起，形成类似于波浪的形状，从而使立管顶部与触地点分离[3]，以减小外部载荷对触地点的影响。

深水油气田开发及混输工艺要求立管可以输送较大流量的气液混合物[4-5]。在输送过程中气液混合物与立管的流固耦合作用机理很复杂，可能会造成立管的参数共振或组合共振，这使得流体引起的立管动力响应问题很难预测。如果长时间振动容易造成立管疲劳损伤甚至发生破裂，导致油气泄漏，从而给国家经济和海洋资源带来严重影响[6]。因此，研究气液两相流作用下缓波形立管的动力响应问题对保护海洋立管系统具有重要意义。J.L.RIVERIN等[7]对复杂结构管道进行了试验，认为虽然内流对管道冲击力很小，但会导致其剧烈振动。XING L.C.等[8]、YE J.等[9]、LUO X.M.等[10]和LI N.L.等[11]分别对不同结构管道的段塞流现象展开试验，并对其持液率、周期和压力等参数进行了分析。B.I.STUART[12]基于能量守恒定理，建立了含有油气水三相流垂直上升管的压力梯度表达式。刘昶等[13]为了识别海洋立管系统中可能出现的流型及考察立管系统在各流型作用下的动态响应,利用室内试验装置模拟海洋立管系统,对立管中两相流动压力波动及其引起的管道振动位移进行了测试。谢翠丽等[14]为研究气液两相混输管道内流导致管道破坏的机理，利用 ANSYS Workbench 软件，建立了L形弯管有限元模型和气液两相CFD模型，进行了L形弯管内流致振的流固耦合数值模拟。杨思齐等[15]对高压管汇弯管部位压裂液固液两相流动及流固耦合效应进行了研究，认为随支撑剂质量浓度和流速增大，流固耦合效果越来越明显，弯管剪应力和变形程度增加，其中流速能显著影响弯管流固耦合程度。马天麒等[16]对内输多相流立管在内流与外部绕流耦合作用下的振动响应进行分析，建立了内部多相流-立管-外部绕流的耦合方程,并采用广义积分变换法将偏微分方程转化为常微分方程进行求解。

以上研究均未考虑缓波形立管中气液两相流引起的立管流致振动问题。为此，笔者建立了缓波形立管的两相流模型，在不同工况下进行了数值模拟分析，模拟结果可为缓波形立管的振动和疲劳特性评估提供指导。

1 模型建立

1.1 几何模型建立

缓波形立管主要包括悬垂段、浮子段和下降段。为了保证流体流动的完整性，又添加了连接井口的下倾管，它与前面3段共同组成了局部缓波形立管系统模型，具体尺寸如表1所示。模型尺寸均根据相似理论计算所得，保证了模型的合理性。立管模型材料为PVC软管，其参数为：弯曲刚度36 N·m2，密度1 570 kg/m3，弹性模量3.2 GPa。下倾管的左边界设置为两相流质量流量入口，悬垂段的上边界设置为压力出口。为了研究两相流立管的动力响应问题，分别选取P1、P2、P3和P4等4个关键点进行监测。缓波形立管模型如图1所示。

表1 缓波形立管模型尺寸 mmTable 1 Dimension of lazy-wave riser mm

图1 缓波形立管模型Fig.1 Model of lazy-wave riser

1.2 边界条件设置

将下倾管左边界端面设为固支，悬垂段上边界端面设为简支，立管内壁面设为流固耦合面，用来传递计算数据。模拟总时长根据实际情况设定，时间步长设为0.05 s。当气液相流速较慢时，为保证流动的完整性，将会适当延长模拟总时长，时间步长保持不变。

1.3 湍流模型

有限元模拟最常用的模型是湍流模型。湍流模型可细分为雷诺应力模型和涡黏模型，工程应用最普遍的是涡黏模型。通过引入湍流黏度，利用Boussinesq假设，将雷诺应力与湍流黏度联系起来，其关系式为：

(1)

式中：σij为Kronecker函数，湍流黏度μt通常使用k-ε模型、k-ω模型和Spalart-Allmaras模型，u为湍流流体的速度，ρ为流体的密度。

(2)

式中：k为湍流动能；ε为湍流耗散率；Cμ为经验系数，通常取0.09。其中湍流动能以及湍流耗散率可以用以下方程进行求解。

湍流动能方程为：

(3)

湍流耗散率方程为：

(4)

式中：Gk为层流速度梯度而产生的湍流动能；Gb为浮力产生的湍流动能；YM为过度扩散产生的波动；C1ε、C2ε、C3ε为经验系数，分别取1.44、1.92和0；σk为k方程的湍流普朗特数，取1.0；σε为ε方程的湍流普朗特数，取1.0；Sk、Sε为自定义。

上述模型经验系数均来自于对前人试验的总结，可以在大部分工况下使用。

1.4 工况参数设置

从文献[17]中选取出部分试验工况，并结合实际生产情况设置了4组模拟工况，如表2所示。

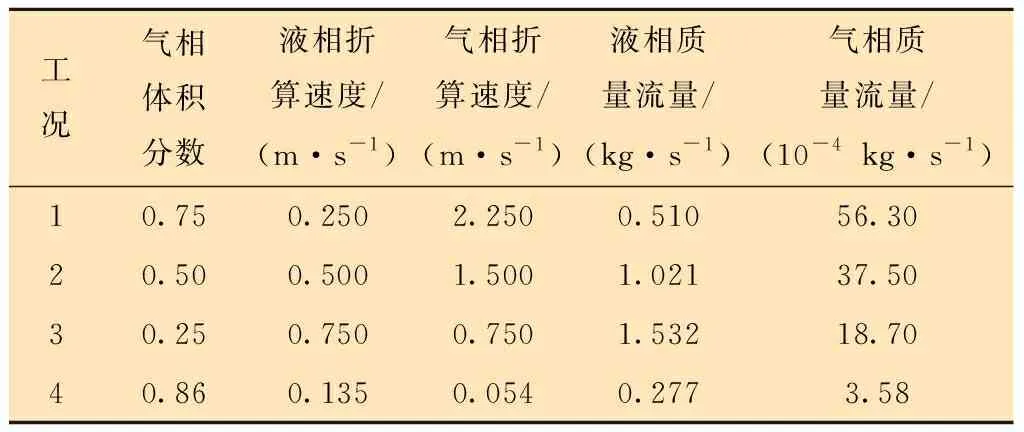
表2 工况参数Table 2 Parameters of working conditions

1.5 网格收敛性分析

网格划分时，将网格尺寸控制在小于水泡直径3.5 mm。立管壁面边界层设为5层，总网格数为188 541，如图2所示。划分的网格质量均大于0.4，其中99.74%以上的网格质量在0.93以上，达到模拟要求。

图2 有限元模型Fig.2 Finite element model

继续将网格加密，将立管壁面边界层设置为10层，并对立管弯曲处进行网格加密处理，得出新的数值模型的网格总数量为537 482，网格质量均大于0.6。利用两套数值模型分别针对工况1进行数值模拟，通过监测同一位置的振动位移，分析网格质量对计算精度的影响，从而选择最佳的数值模型进行剩余工况的计算。

目前，我国职业经理人市场存在的问题是：职业化程度低、数量少、法律法规体系不健全、企业主和经理人的信任体系没有建立起来、认证和评价体系还没有各方的认可。这就导致企业在选聘职业经理人时获取信息存在问题。

图3为工况1下未加密的数值模型在计算过程中的迭代收敛情况。图3纵坐标表示以10为底的对数收敛范数。由图3可以看出迭代至200步左右收敛。图4为两套数值模型在P2监测点处的Y向位移对比。从图4可以看出，两套数值模型计算结果差异很小，说明未加密的数值模型计算精度也比较高。因此，为了提高计算效率，使用未加密的数值模型计算剩余工况。

图3 计算收敛图Fig.3 Calculation convergence diagram

图4 两套模型在P2点Y向位移对比Fig.4 Y-direction displacement comparison of P2 between two models

2 气液两相流缓波形立管数值模拟

2.1 下倾管内气液相分布

分别模拟入口气相体积分数为0.75、0.50和0.25的工况，具体参数如表2中的工况1、2、3所示。模拟得到距离下倾管入口3、6和9 m处截面的气液相分布，如图5～图7所示，分析了不同入口气相体积分数对下倾管内部两相流流型的影响。

图5 工况1不同位置截面气液相分布Fig.5 Gas and liquid distribution at different cross sections under working condition 1

从图5～图7可以看出，随着入口气相体积分数的变化，管内流型也发生变化。其中距离流体入口越远的截面其含气体积分数越高，但总体来看，同一工况中下倾管各截面的气液体积分数波动不明显。工况1下倾管中的液相体积分数都在0.748 9～0.751 7之间，说明整个管内气液相都处于混合状态。这是由于工况1下气液相的入口流速悬殊较大，加之液相体积分数比较低，随着管内气体高速流过，带动液相从管道底部脱离，以小液滴的形式与气体混合向前流动，导致下倾管中两相流呈现混合流动状态。工况2下管内两相流开始出现分层流动状态，工况3下管内的两相流分层流动现象更加明显。因此，随着入口气相体积分数的减小，下倾管中更容易出现分层流动现象。

图6 工况2不同位置截面气液相分布Fig.6 Gas and liquid distribution at different cross sections under working condition 2

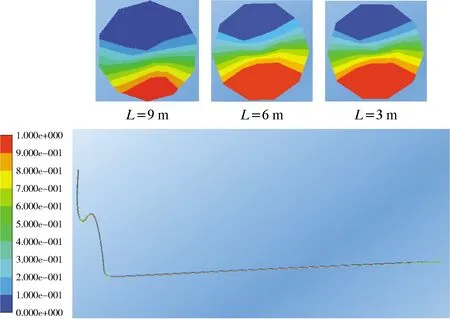
图7 工况3不同位置截面气液相分布Fig.7 Gas and liquid distribution at different cross sections under working condition 3

2.2 缓波形立管中的段塞流

通过对工况4数值模拟，得到缓波形立管中的流体流动状态，如图8所示。从图8可以看出，缓波形立管中已经发生段塞流现象，下倾管中的液相流至缓波形立管下降段底部时，由于惯性力作用液体将快速形成液塞堵住下降段底部，如图8中的细节图(2)所示。因为水比较容易变形，在重力作用下导致液塞回落到下降段底部，此时气体将再次进入下降段。随着液体的连续涌入，下降段底部的液面逐渐升高，促使液塞再次形成。接下来液塞又会在重力和气体冲击作用下被破坏，如此反复，直到下降段底部的液体逐渐升高形成稳定的液柱，如图8中细节图(3)所示。此时，缓波形立管的悬垂段也会因为上述情况形成稳定的液柱，在浮子段形成气塞，如图8中的细节图(4)所示。由于缓波形立管中液柱堵住了气体的通路，所以造成下倾管中几乎被气体充满，如图8中的细节图(1)所示，整个缓波形立管系统就形成了两段比较严重的段塞流。

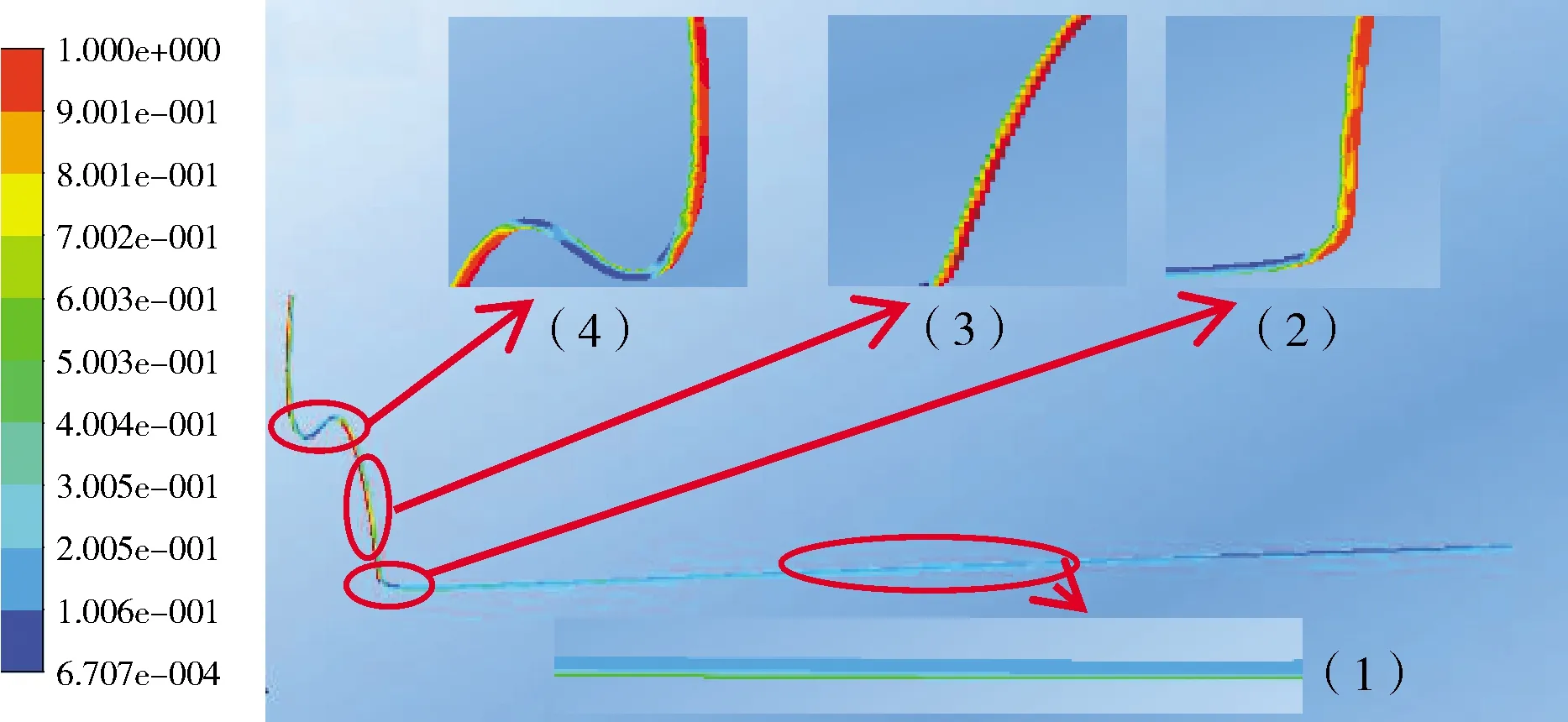
图8 工况4缓波形立管内气液分布Fig.8 Gas and liquid distribution in the lazy-wave riser under working condition 4

由模拟结果可知，立管系统中最大振动位移出现在缓波形立管下降段的底部，因此选择P2为监测点。工况4下，该点在X、Y、Z方向的振动位移和应力如图9～图12所示。

图9 P2监测点在X方向的位移Fig.9 Displacement of monitoring point P2 in X direction

图10 P2监测点在Y方向的位移Fig.10 Displacement of monitoring point P2 in Y direction

图11 P2监测点在Z方向的位移Fig.11 Displacement of monitoring point P2 in Z direction

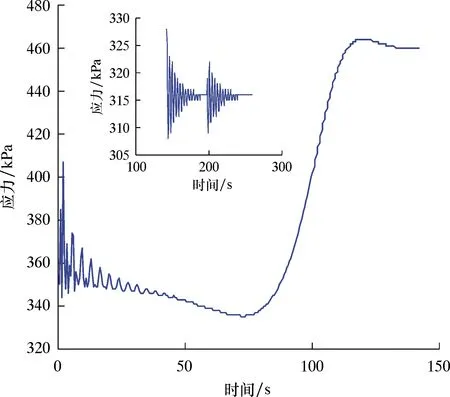
图12 P2监测点所受应力Fig.12 Stress on monitoring point P2

综上所述，工况4条件下立管系统产生比较严重的段塞流流型。由图9～图11可以看出，P2监测点在Y方向的振动位移远大于在X、Z方向的振动位移。当管内两相流流动至142 s左右时，P2点在各方向上的位移均发生了不同幅度的波动。其中，X方向最大位移从2.60×10-6m增长到3.42×10-6m，增幅达到16%。Y方向最大位移从4.2×10-4m增长到4.7×10-4m，增幅达到12%。Z方向最大位移从2.6×10-7m增长到4.55×10-7m，增幅达到75%。由图12可以看出，P2监测点应力值从400 kPa增长到460 kPa，增幅达到15%。这是因为流体流动至142 s左右，段塞流开始喷发，致使立管发生明显振动。由此可见，段塞流的喷发会对立管振动产生比较大的影响。

2.3 入口气相体积分数对管道振动响应的影响

通过对比工况1、2、3的模拟结果发现，缓波形立管最大振动位移同样出现在P2监测点，其在X、Y、Z方向上的位移时程曲线如图13～图15所示。从图13～图15可以看出：在流动的初期3种工况下，管内流体在X、Y、Z方向均产生较大的振动位移，其中Y方向的位移远大于X和Z方向，这是因为管内两相流流动初期不稳定；随后各工况的振动位移逐渐发生衰减直至稳定振动，此时Y方向的振幅均大于X和Z方向，且振动频率基本保持不变，其中工况1下的振幅均远大于工况2和工况3。

图13 P2监测点在X方向的位移Fig.13 Displacement of monitoring point P2 in X direction

图14 P2监测点在Y方向的位移Fig.14 Displacement of monitoring point P2 in Y direction

图15 P2监测点在Z方向的位移Fig.15 Displacement of monitoring point P2 in Z direction

工况1、2、3下立管系统所受应力分布如图16～图18所示。由图16～图18可以发现：3种工况下立管系统的最大应力均出现在流体入口的固支端；工况1的最大应力为11.250 MPa，工况2的最大应力为6.679 MPa，工况3的最大应力值为4.629 MPa。对比3种工况下立管所受应力极值可以发现，随着气相体积分数的增大，立管所受应力极值持续增大，而当入口气相体积分数从0.50增加到0.75时，P2监测点所受的应力极值有大幅增大。

图17 工况2立管应力云图Fig.17 Stress cloud of riser in working condition 2

图18 工况3立管应力云图Fig.18 Stress cloud of riser in working condition 3

综上所述，工况1下立管的振幅和应力极值较其他两种工况均有大幅增长。其主要原因是当入口气相体积分数为0.75时，立管系统的响应频率与其一阶固有频率吻合，立管发生了共振现象，同时也表明改变两相流的流动参数可以引发立管共振。

3 结 论

本文建立了气液两相流缓波形立管的双向流固耦合模型，应用k-ε湍流模型，通过设置不同入口气相体积分数和入口质量流量模拟了4种工况，分析了不同的入口边界条件对缓波形立管系统中流型变化和管道振动响应的影响，得出以下结论。

(1)工况1中下倾管内两相流流型为气液混合流动，工况2和工况3为气液分层流动，随着入口气相体积分数的减小，下倾管中的分层流动现象更明显。

(2)缓波形立管中出现了两段比较严重的段塞流。段塞流的喷发加剧了立管的振动，入口气液相流量较小时更容易形成严重段塞流。

(3)工况1、2、3下Y向振幅远大于X和Z方向振幅，其中工况1导致立管的振动强度最大。3种工况下立管所受的最大应力均处在流体入口的固支端。

(4)当入口气相体积分数从0.50增加到0.75时，立管的振动位移和最大应力均发生大幅度增长，这是因为立管系统响应频率与其一阶固有频率吻合，导致立管发生了共振现象。