确定岩石抗钻特性空间分布规律的新方法*

胡棚杰 李忠慧 蒋战峰 楼一珊 杨明合 张 艳

(1.长江大学石油工程学院 2.长江大学油气钻井技术国家工程实验室防漏堵漏研究室 3.新疆贝肯能源工程股份有限公司)

0 引 言

钻井是油气勘探开发最重要、最直接的手段，而机械钻速低和钻井周期长等难题严重制约了钻井开发进程。地层岩石力学特性的分布规律研究，尤其是岩石抗钻特性空间分布规律的研究是解决这些难题的关键。地层岩石抗钻特性参数包括单轴抗压强度、岩石硬度和岩石可钻性等指标[1-4]。只有清楚地了解和掌握地层的岩石抗钻特性空间分布规律，才能有针对性地优化井身结构、优选钻头和应用钻井提速配套技术等[5-7]，从而缩短钻井周期。

目前，主要通过两类方法确定地层抗钻特性分布规律[8-13]：一类是利用测井资料确定岩石抗钻特性，首先通过室内试验测定区域内岩石抗钻特性参数，建立测井数据与岩石抗钻特性参数的联系，再根据区域内多口井的测井数据，采用曲面拟合方法建立某一特定深度岩石抗钻特性分布情况。最小二乘法[9]、神经网络法[10]和有限元法[11]等方法只能建立某一特定深度的岩石抗钻特性参数统计剖面，不能建立岩石抗钻特性的空间分布规律，且假设某区域内岩石抗钻特性在同一深度连续，没有考虑不同井位之间地层厚度和海拔高度不同对岩石抗钻特性空间分布规律的影响，这与地层实际情况不符。另一类是利用地震资料预测岩石抗钻特性。根据岩石自身属性与声波速度的良好相关性，利用地震资料反演层速度建立地层相对抗钻特性能力的分布情况。如利用叠加速度谱或测井约束的地震资料反演处理等操作得到层速度，利用层速度预测岩石的抗钻特性[12-13]。该类方法受限于地震资料的频带范围，提取数据分辨率不高，通常只能反映地层抗钻特性能力变化的趋势，在缺乏测井资料的新井区内应用可以给现场施工提供参考，但在定量分析上精度不如第一类方法。

针对第一类方法的不足之处，笔者在前人研究的基础上，提出一种能够解决同一深度岩石抗钻特性分布不连续及应用测井资料不能建立岩石抗钻特性空间分布规律问题的新方法。该方法将空间分布问题转化为纵横分布问题，通过纵向深度分层归一化处理实现地层抗钻特性在横向分布上的连续性，通过层深坐标系实现岩石抗钻特性横向分布规律的纵向叠加，从而形成一种分析岩石抗钻特性空间分布规律的新方法。研究结果可为钻井提速方案的制定提供重要参考。

1 基于测井数据的岩石抗钻特性参数分析模型

1.1 岩石抗钻特性参数室内试验

为建立岩石抗钻特性参数与测井数据之间的关系，对取自玛湖凹陷百口泉组地层的岩心进行室内试验，包括岩石单轴抗压强度、硬度和可钻性级值的测定，试验结果如表1和表2所示。

表1 玛湖凹陷区域岩石单轴抗压强度测试结果Table 1 Test results of uniaxial compressive strength of rocks in Mahu sag

表2 玛湖凹陷区域岩石硬度及PDC微可钻性级值测试结果Table 2 Test results of hardness and PDC micro-drillability grade of rocks in Mahu sag

1.2 岩石抗钻特性参数模型建立

地层岩石力学特征由岩石自身结构性质所决定，根据岩石结构特征选择合适的关系模型是保证参数计算精确的前提。玛湖凹陷百口泉组储层属于特低孔低渗砂砾岩油藏[14-15]， 根据前人[16-17]对岩石力学参数与储层类型的关系认识，在孔隙度0.01～0.18的砂砾岩储层中，单轴抗压强度与密度和声波纵波速度的二次幂有较好的相关性，岩石硬度、岩石可钻性级值和纵波时差有较好的指数关系。对试验结果和测井数据进行拟合回归分析，得到相关参数的计算模型，如图1～图3所示。

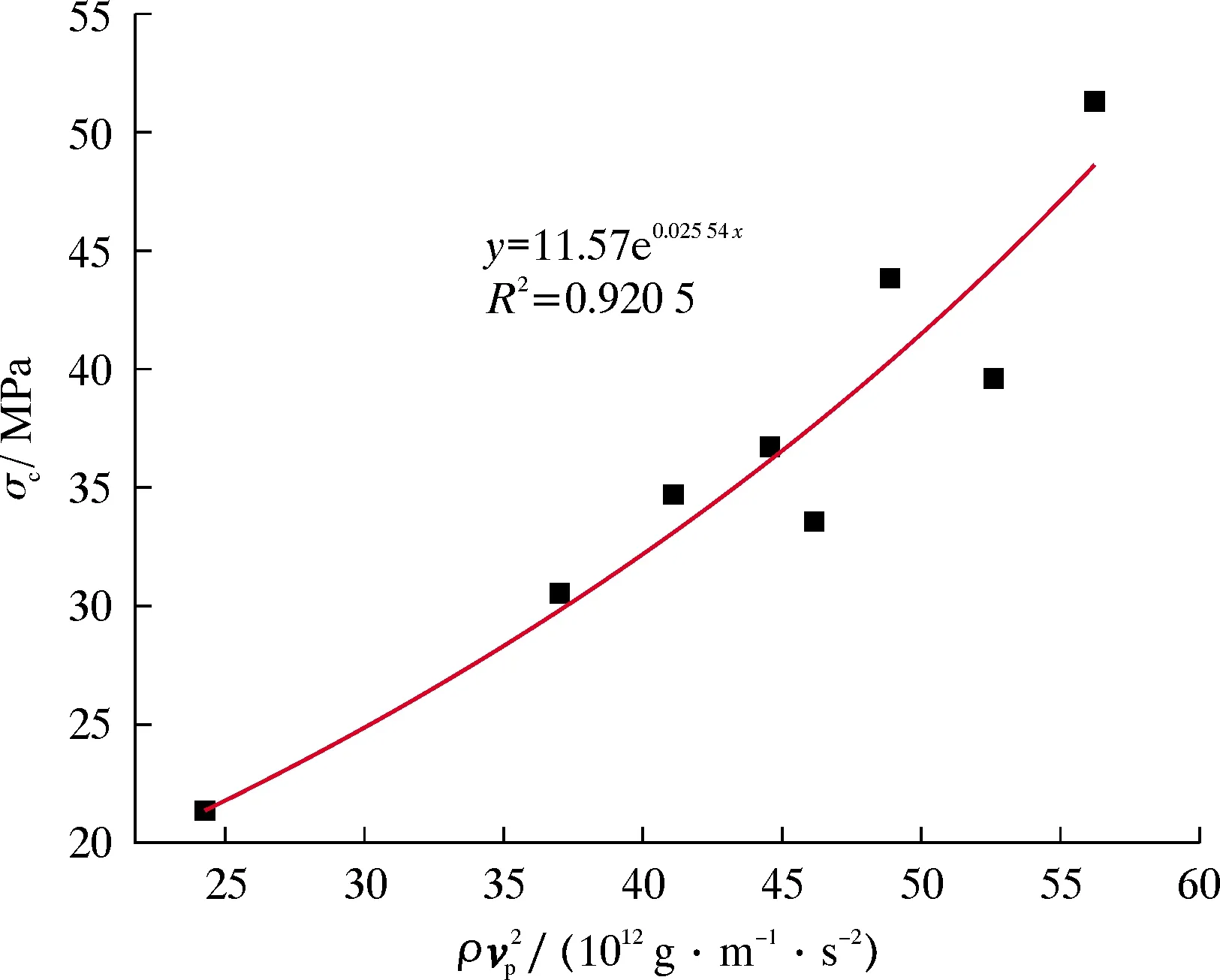
图1 单轴抗压强度与密度和声速的二次幂关系曲线Fig.1 Relationship between uniaxial compressive strength and the quadratic power of density and acoustic velocity

图2 硬度值与声波时差的关系曲线Fig.2 Relationship between hardness and interval transit time

图3 PDC微可钻性级值与声波时差的关系曲线Fig.3 Relationship between PDC micro-drillability grade and interval transit time

岩石单轴抗压强度计算模型为：

(1)

岩石硬度计算模型为：

Py=328 091e-0.026 2Δtp

(2)

PDC钻头可钻性级值计算模型为：

Kd=59.723 6e-0.011 3Δtp

(3)

式中：σc为单轴抗压强度，MPa；ρ为岩石密度，g/cm3；vp为纵波在地层中传播的速度，km/s；Py为岩石硬度值，MPa；Kd为岩石PDC微可钻性级值，无量纲；Δtp为声波纵波时差，μs/m。

2 岩石抗钻特性空间分布规律确定

基于上述参数计算模型，可由同一区块内参考井的测井数据计算地层岩石抗钻特性参数。对于单口井而言，地层岩石抗钻特性参数的分布规律是指以井深为纵坐标、以岩石抗钻特性参数为横坐标的一条曲线，如图4所示；对于2口井而言，地层岩石抗钻特性参数的分布规律是指过2口井井轴线的二维平面，2口井之间通过连井曲线实现，如图5所示；对于3口井及以上，需要岩石抗钻特性参数的三维空间分布才能描述抗钻特性，下面将介绍这种方法。

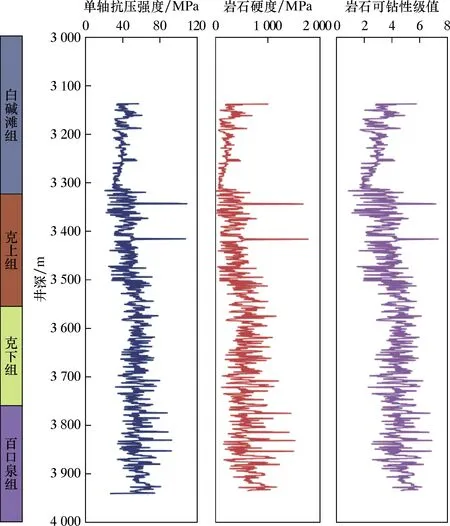
图4 X井岩石抗钻特性参数纵向分布规律Fig.4 Vertical distribution law of rock anti-drilling characteristic parameters in Well X

图5 X-Y井连井抗钻特性参数平面分布规律Fig.5 Plane distribution law of anti-drilling characteristic parameters in Well X-Y

2.1 纵向深度分层归一化处理法

W.R.TOBLER[18]于1970年提出地理学第一定律——空间相关性定律，指任何与地理相关事物或属性在空间分布上都具有相关性。这种地物之间的相关性与距离有关，一般来说，距离越近，地物间相关性越大；距离越远，地物间相异性越大。根据该定律，若使相邻井位之间同一深度的地层形成时间相同，则地层岩石抗钻特性分布在这同一深度上(距离最短)连续性最好。因此需要消除不同井位地层厚度和海拔高度不同对空间连续性的影响。笔者按照地质分层对纵向深度进行归一化处理，从而解决岩石抗钻特性参数的纵向分布问题和同一深度的连续性问题。

纵向深度分层归一化处理具体内容如下。首先以每口井的地面为基准起始点，向下以层位为单元，每个层位的底界为刻度，建立向下为正的层位坐标系，下文将这种坐标称为层深坐标系。在层深坐标系内，所有井的地面起始高度都为0，在浅层地表认为地层形成时间相同，这样就消除了不同井位海拔高度对地层连续性的影响。设向下第1个层位的底界层深为1，第2个层位的底界层深为2，以此类推，第n个层位的底界层深为n，则第n个层位的实际深度范围就在层深(n-1)～n之间。将地层实际深度按线性关系映射到地层层深坐标上，建立层深与地层深度的一一对应关系。在同一层深处，即使不同井位处的地层深度和厚度不同，但地层形成的时间相同。相邻井位之间的地层岩石属性的相关性最高，在井之间的插值精确度就最高。层深坐标系如图6所示。

图6 地层归一化处理——层深示意图Fig.6 Stratigraphic normalization: sketch of layer depth

2.2 横向抗钻特性克里金插值法

通过层深坐标系消除了地层厚度和海拔高度对岩石抗钻特性不连续的影响，则在同一层深坐标值下，地层形成时间不同的影响就被最小化，地层岩石属性就存在整体均一性和局部差异性，地层岩石抗钻特性横向分布规律就转化成空间曲面拟合问题。在空间连续属性分布的随机过程中，克里金插值法能给出最优线性无偏差估计，在地质统计学中也被称为空间最优无偏估计[19]。克里金插值法由法国地质统计学家Matheon[20-21]提出，被应用于地表(地层形成时间相近)事物现象的分布中。笔者首次提出将克里金插值法应用于地层岩石抗钻特性的空间分布规律描述中，在纵向上地层归一化处理后，该方法可以应用于其他与地理相关的事物和属性上，具有普适性。

不同克里金插值法具有不同的假设条件，根据地层岩石属性的整体均一性和局部差异性选择使用普通克里金插值法，普通克里金插值法假设空间属性z均一，对于空间内任意一点(x,y)的空间属性z都有同样的期望c与方差σ2， 即对任意一点(x,y)都有：

E[z(x,y)]=E[z]=c

(4)

Var[z(x,y)]=σ2

(5)

对于空间上某一点(xo,yo)来说，其空间属性zo为空间上所有已知点的数据加权求和，即：

(6)

3 实例分析

为验证新方法的准确性，采用新方法对准噶尔盆地玛湖凹陷内某区块进行岩石抗钻特性空间分布规律预测分析。在该区域内选取5口参数井(A～E井)作为分析对象，将区域内参考井和试验井的大地坐标值转化为局部相对坐标(见表3)，建立百口泉组地层的岩石抗钻特性参数空间分布规律，实施步骤如下。

表3 参数井的井位坐标简化Table 3 Coordinate simplification of parameter wells

(1)对参数井进行纵向深度分层归一化处理，建立每口井各层位实际深度与归一化层深之间的对应关系，如表4所示。

表4 地层深度归一化预处理Table 4 Pretreatment of stratum depth normalization

考虑到百口泉组地层实际厚度在200 m左右，以20 m为间隔能满足抗钻特性参数空间纵向分布规律精确度，在层深9～10之间以0.1为增量分为10小层，每个小层实际厚度20 m左右。

(2)在每个层深单元刻度内找到每口井实际深度对应测井数据，利用抗钻特性参数计算模型得到每口井每个层深内的抗钻特性参数均值，这个均值代表这口参数井在这一层深单元深度的岩石抗钻特性能力，计算结果如表5所示。

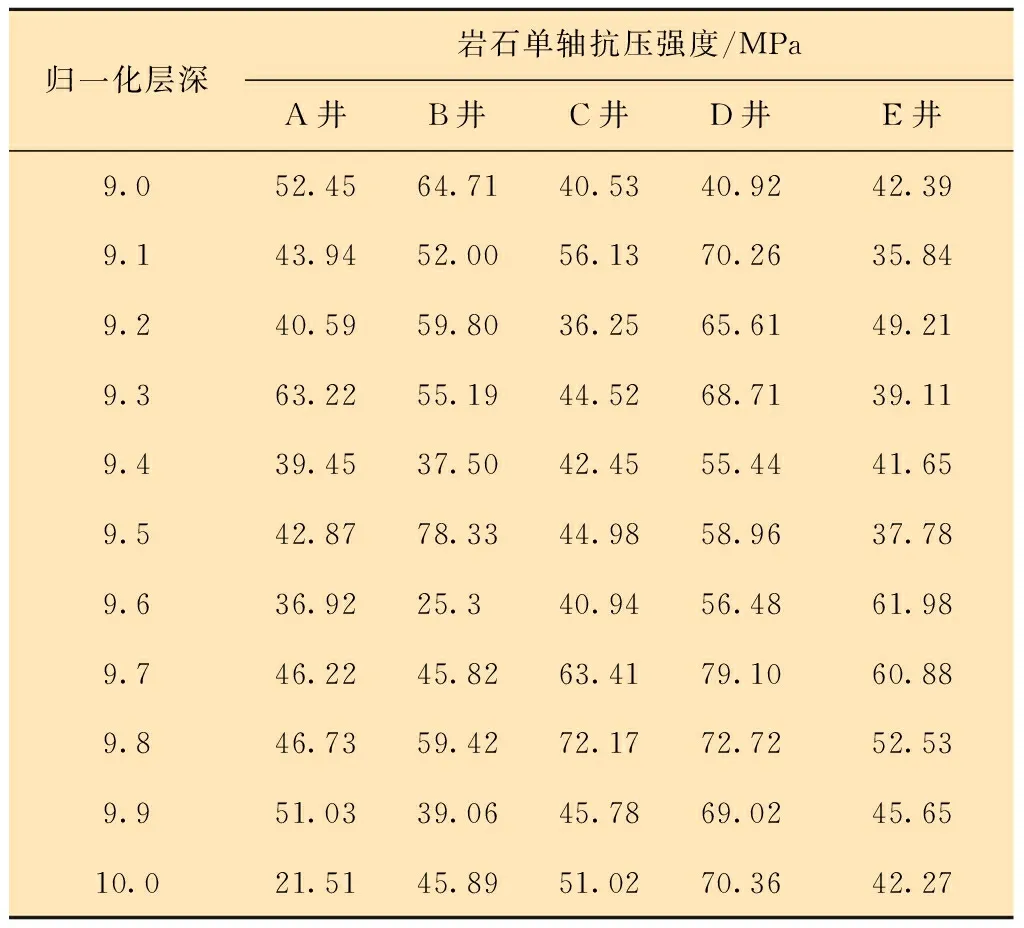
表5 百口泉组地层抗钻特性参数Table 5 Anti-drilling characteristic parameters of Baikouquan Formation

(3)在同一层深刻度上，以5口参数井为基础，应用克里金插值法建立岩石抗钻特性参数横向分布规律，每个层深单元通过层深坐标在纵向上联系，这样得到百口泉组地层岩石抗钻特性参数的空间分布规律，如图7～图9所示。

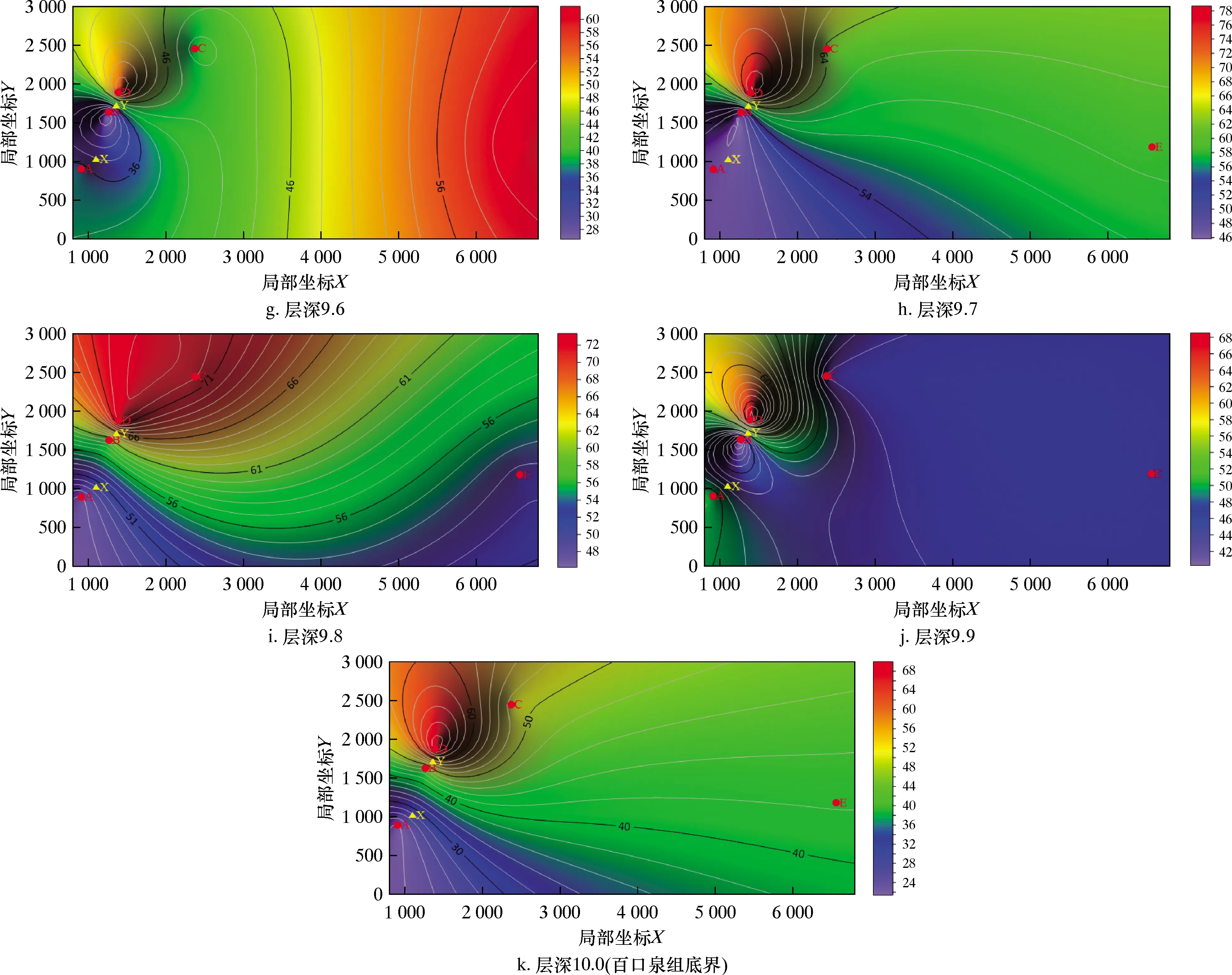
图7 百口泉组地层岩石单轴抗压强度空间分布规律Fig.7 Spatial distribution law of uniaxial compressive strength of Baikouquan Formation rocks

图8 百口泉组地层岩石可钻性级值空间分布规律Fig.8 Spatial distribution law of drillability grade of Baikouquan Formation rocks

在建立的岩石抗钻特性分布区域内选择两口试验井(X井和Y井)进行验证。试验井的岩石抗钻特性参数纵向剖面如图5所示，试验井的测井数据未参与空间抗钻特性参数分布规律的建立，仅用于预测结果对比，以验证该方法的有效性。从图7～图9中可以读取X井和Y井在百口泉组地层的抗钻特性参数预测值，将其与图5中的纵向单井抗钻特性参数试验值做对比分析，试验结果和预测结果对比如表6所示。

表6 抗钻特性参数试验结果与预测结果对比Table 6 Comparison between the tested anti-drilling characteristic parameters and the predicted results

从表6可以看出，X井和Y井在岩石抗钻特性参数空间分布上的平均预测误差小于10%，能够较好地满足工程分析精度要求；Y井的预测精度整体高于X井，其原因是Y井距离B井和D井较近，利用克里金插值法在各层深中建立横向分布规律时，参数井对于Y井的约束力大于X井，这与克里金插值法原理吻合，增添参数井的数量可以提高X井的预测精度。因此，该方法在岩石抗钻特性参数的空间分布确定上精度较高，可以有效反映地层抗钻能力的空间分布，能为制定钻井提速方案提供参考。

4 结论与认识

(1)在室内试验的基础上，建立了岩石抗钻特性参数与测井数据的分析计算模型。该模型根据玛湖凹陷百口泉组储层特点建立，可为玛湖凹陷百口泉组地层岩石抗钻特性分析提供参考。

(2)将地层岩石抗钻特性参数空间分布规律问题转化为纵横分布问题，采用的纵向深度分层归一化处理法和横向抗钻特性克里金插值法实现了岩石抗钻特性的空间分布规律确定，为优化井身结构、优选钻头以及应用钻井提速配套技术等提供了重要的技术手段。

(3)利用本文提出的方法对玛湖凹陷百口泉组地层岩石抗钻特性空间分布规律进行预测，预测精度达到了90%以上，满足工程设计精度要求，能够为钻井提速方案的制定提供参考。

(4)虽然通过该方法可以确定任何与地理事物和属性相关参数的空间分布规律，但该方法受限于建立横向剖面参数井的数量，参数井越多则预测精度越高。