Environmental noise beside an elevated box girder bridge for urban rail transit*

Yun-fei ZHANG, Li LI, Zhen-yu LEI, Long-bo YU, Zheng BU

Environmental noise beside an elevated box girder bridge for urban rail transit*

Yun-fei ZHANG1,2, Li LI†‡1,2, Zhen-yu LEI1,2, Long-bo YU1,2, Zheng BU1,2

Institute of Rail Transit, Tongji University, Shanghai 201804, China Shanghai Key Laboratory of Rail Infrastructure Durability and System Safety, Shanghai 201804, China †E-mail: lilee@tongji.edu.cn

Noise generated by trains running on elevated lines creates many disturbances to the normal lives of surrounding residents. Investigations have shown that people living along elevated lines complain that the noise is sometimes unbearable. To better control the noise and optimize the acoustic environment, noise spectrum characteristics were analyzed and compared with a field test and a numerical simulation. Through an energy analysis of the noise on the bridge side, the energy distribution characteristics of the noise at specific measuring points in different frequency bands were obtained. The influence of the Doppler effect on frequency shift was analyzed. Based on the partial coherence theory, a multi-input and single-output program was compiled to calculate the correlation and contribution degree of the bridge structure-borne noise and wheel/rail noise at the one-third octave center frequency. The results show that the peak noises of the bridge and the wheel/rail are concentrated at 31.5–63 Hz and 400–800 Hz, respectively. For environmental noise on the bridge side, the frequency band above 250 Hz is mainly affected by the wheel/rail noise. In areas of noise source strength, the relative ratio of noise energy above 250 Hz can reach 83.4%. Noise in the near ground and far bridge area is mainly low-frequency, and the relative energy ratio is about 8.9%. The Doppler effect has an influence of less than 6% on the frequency shift with a speed of 67.9 km/h. In the low-frequency band below 250 Hz, the noise in the acoustic shadow area near the bridge and the ground is mainly contributed to by the vibration-radiated noise of the bridge, of which the contribution of the bottom panel is the most prominent. The noise in the comprehensive noise area of the far bridge is mainly caused by the structure-borne noise of the bridge, and the contribution of each bridge panel is different. This study can provide a reference for finding the source of elevated rail noise in some challenging frequency ranges and for then determining optimal designs and measures for noise reduction.

Urban rail transit; Elevated line; Environmental noise; Box girder bridge; Field measurement; Acoustic model; Doppler effect

1 Introduction

In recent years increasing attention has been paid to environmental noise from urban rail transit. Compared with underground lines and ground lines, urban rail transit elevated lines have the advantages of low investment costs, rapid construction, low operating costs, and low project risks. They are increasingly favored in government planning and construction. However, elevated lines have, to a certain degree, impacted the urban environment. In particular, vibration and noise problems generated by the operation of trains have strongly interfered with the normal lives of surrounding residents (Thompson and Jones, 2000; Zhao and Wang, 2018; Kouroussis et al., 2019). The structural noise of viaducts is mainly low- frequency noise with a long wavelength and thus the strong ability to bypass buildings and other structures, resulting in a large propagation range and slow attenuation (Remington, 1976; Ford and Thompson, 2006). For people with long-term exposure to such an environment, it presents an increased risk of neurasthenia, insomnia, depression, and other problems, seriously endangering their health.

The noise problem of elevated line rail transit is a system problem, involving sound generation, propagation, and arrival. Usually, sound barriers are used to meet the requirements of sound environments (Li et al., 2012, 2014; Song and Li, 2018); in some areas, rail vibration isolation measures are also used. However, residents along rail transit elevated lines still complain about the impact of noise. The difference between the noise reduction index and residents’ feelings about noise is related to the use of an A-weighted evaluation. Thompson (2013) showed that no persuasive correlation was found between A-weighted noise and a perceived acoustic comfort evaluation. That is, the effect of low-frequency noise on people is underestimated. Human tolerance to noise is influenced by many factors, including the total noise level, the maximum noise, the background noise, and the spectral characteristics of the noise (Rimell et al., 2015). The noise source and propagation paths are different, and the noise frequency range for vibration and noise reduction products also differs, which complicates the noise problem (Kitagawa and Thompson, 2006). Therefore, the basis of noise control and acoustic environment optimization is to analyze the sources, spatial distribution, and influencing factors of environmental noise on the viaduct side.

The main source of urban rail transit elevated line noise is wheel/rail noise and bridge vibration radiation noise. Research on the environmental noise of rail transit viaducts focuses on vehicle-track-bridge coupling vibration, wheel/rail noise theory, radiated noise from viaduct structure vibration, noise testing, and bridge structure noise identification and prediction. Part of the research mainly studied structure- borne noise in respect to bridge types, geometric sizes, non-ballast track types, fasteners, vehicle types, and other factors, focusing on the evaluation of the overall environmental noise level (Ngai and Ng, 2012). Another part of the referenced experimental research not only focused on the noise level at different locations, but also tested structural vibration, paid attention to the mechanisms of low-frequency noise emitted by structural vibration, and explored the refined frequency-domain characteristics of vibration and noise (Landström et al., 1995; Ma, 2007; Ngai and Ng, 2012). Due to the complexity of noise generation and radiation, it is difficult to approximate its characteristics with a simple model. Therefore, it is necessary to obtain noise characteristics through experiments and analyze its radiation characteristics from different points of measurement.

The aim of this study is to provide a reference for the optimization of noise reduction of the rail viaduct at certain sensitive frequencies. The approach is combined experimental measurement and numerical simulation. In addition to bridge side noise, direct noise radiated from bridge structure and wheel/rail noise were also measured and used to thoroughly investigate the source of noise at specific frequencies.

2 Field measurement process

Based on a field test of an elevated metro line, an ordinary slab track was taken as the study object. The propagation and attenuation of environmental noise beside the box girder bridge were analyzed using time domain, frequency domain, and one-third octave analysis.

2.1 Description of measurements

A series of measurements were taken in a city in east China. The operating line is a monolithic track bed with type WJ-2A fasteners. The gauge is standard and the elevated structures are double-line simply- supported box girder bridges. The total length of the box girder is 30.00 m. The depth of the box girder is 1.80 m. The deck width of the box girder is 9.60 m. The width of the bottom slab is 4.50 m. The width of the flange is 2.34 m. There are green belts beside the line within 13.00 m, and a two-way, six-lane road within 13.00–55.00 m on which cars, buses, and occasionally some heavy trucks pass by.

The operating train consists of six metro vehicles, comprised of four power cars and two trailer cars, with an axle load of 140 kN. The nominal wheel rolling diameter is 0.84 m. The length between bogie centers is 12.60 m. The wheelbase of the bogie is 2.30 m. The length of the trailer vehicle with a driver cab is 19.65 m. The length of the motor vehicle is 19.00 m, the width is 2.89 m, and the maximum speed is 80 km/h.

For measurement, the B&K 4189 sonic transducer (measuring range is 6–20 kHz), B&K 2671 microphone preamplifier (20–50 000 Hz), the piezoelectric acceleration sensor (50, 500, 100), and vibration and noise collectors were used. Test conditions and train speeds are shown in Table 1. Noise measuring points are shown in Fig. 1.

2.2 Noise analysis of measuring points on the bridge deck

The noise of the bridge deck in the 20–2000 Hz frequency range is shown in Fig. 2. The results show that there are multiple peaks at middle-high frequencies above 200 Hz. The noise of the wheel/rail measuring point (S1, which is 1.60 m away from the centerline of the track and 0.45 m above the rail surface) shows local peaks at 400, 500, and 630 Hz. The measuring points of the bottom slab (S2), the web (S3), and the flange (S4) also show relative peaks at 40, 400, and 630 Hz. Compared with the noise generated by the wheel/rail system, the impact of the bridge structure is weaker. The maximum difference in the middle-high frequency range is about 30 dB.

Table 1 Test conditions and train speeds

Fig. 1 Layout diagram of noise measuring points

Fig. 2 Bridge deck noise spectrum diagram

It can be seen that the wheel/rail noise is significantly higher than the radiated noise of each slab in the frequency of 20–40 Hz and 63–200 Hz, while the peak of the radiated noise of the bridge structural slab is concentrated in the range of 31.5–63 Hz.

2.3 Distribution of environmental noise beside the box girder bridge

The horizontal distribution and propagation pattern of environmental noise beside the box girder are shown in Fig. 3.

It shows the distribution and variation of one-third octave curve noise at the height () of 1.2, 9.8, 11.3, and 12.8 m, respectively. In general, the sound pressure level at=7.5 m is the highest, followed by=22 m, with the lowest at=55 m (is the horizontal distance from the centerline of up-line track). However, near the height of 1.2 m above the ground, when the noise frequency is greater than 250 Hz, the sound pressure level at=22 m is greater than that at=7.5 m. Due to the shielding effect of the box girder and parapet, there is a small difference between noises at=7.5 m and=22 m, when the height of the measuring point is 9.8 and 11.3 m, respectively. In addition, the acoustic reflection effects of different ground surfaces need to be considered. Thereis a green belt with soft soil within 7.5 m of the railway line, so certain sounds are absorbed. In contrast, at=22 m the ground surface is a hard-paved road. The sound reflected from the road surface will be superimposed and amplified in addition to the original.

The vertical distribution and propagation pattern of environmental noise beside the box girder are shown in Fig. 4.

Fig. 4a shows that the sound pressure level of measuring point 1-4 is the largest while 1-1 is the smallest, which is probably due to attenuation and to the shielding effect of the box girder on wheel/rail noise. Peak values are concentrated in the range of 40–63 Hz and 400–800 Hz. It can be seen in Fig. 4b that the peak values of noise are concentrated in the ranges of 50–63 Hz and 400–630 Hz. In the range of center frequencies, 20–800 Hz of the one-third octave, the peak value order is 2-4, 2-1, 2-2, and 2-3 from large to small. In the 40–63 Hz range, the order is 2-1, 2-4, 2-2, and 2-3. Fig. 4c shows that the points of sound pressure levels from large to small are 3-1, 3-4, 3-2, and 3-3 in the range of 40–1000 Hz.

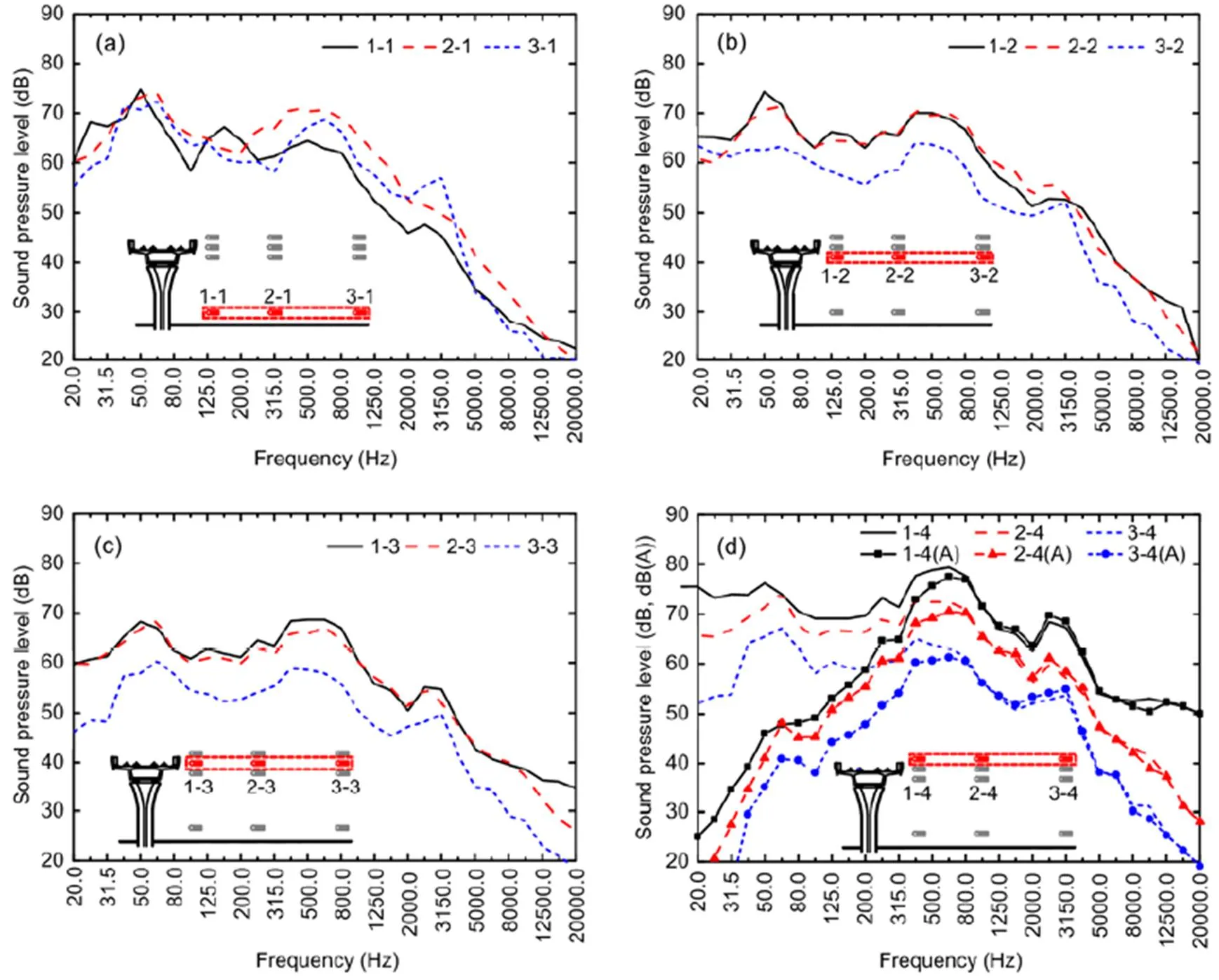
Fig. 3 Horizontal distribution and propagation pattern of environmental noise beside the bridge: (a) h=1.2 m; (b) h= 9.8 m; (c) h=11.3 m; (d) h=12.8 m ((A) means A-weighted)

2.4 Analysis of environmental noise energy distribution on the bridge side

For the elevated box girder bridge without a sound barrier, the environmental noise is mainly composed of wheel/rail noise and the structure-borne noise of the bridge. The analysis in Sections 2.2 and 2.3 shows that the spectrum distribution of the two kinds of noise is different, and that the noise beside the bridge varies with the distance from the line. The structure-borne noise of the bridge is mainly made up of low frequencies. The wheel/rail noise is mainly high-frequency, but its peak overlaps with structural noise in the low-frequency region. Measuring points 1-1, 3-1, 1-4, and 3-4 are selected to represent the area near the ground and the bridge, near the ground and far from the bridge, far from the ground and near the bridge, and far from the ground and the bridge, respectively, as shown in Fig. 5.

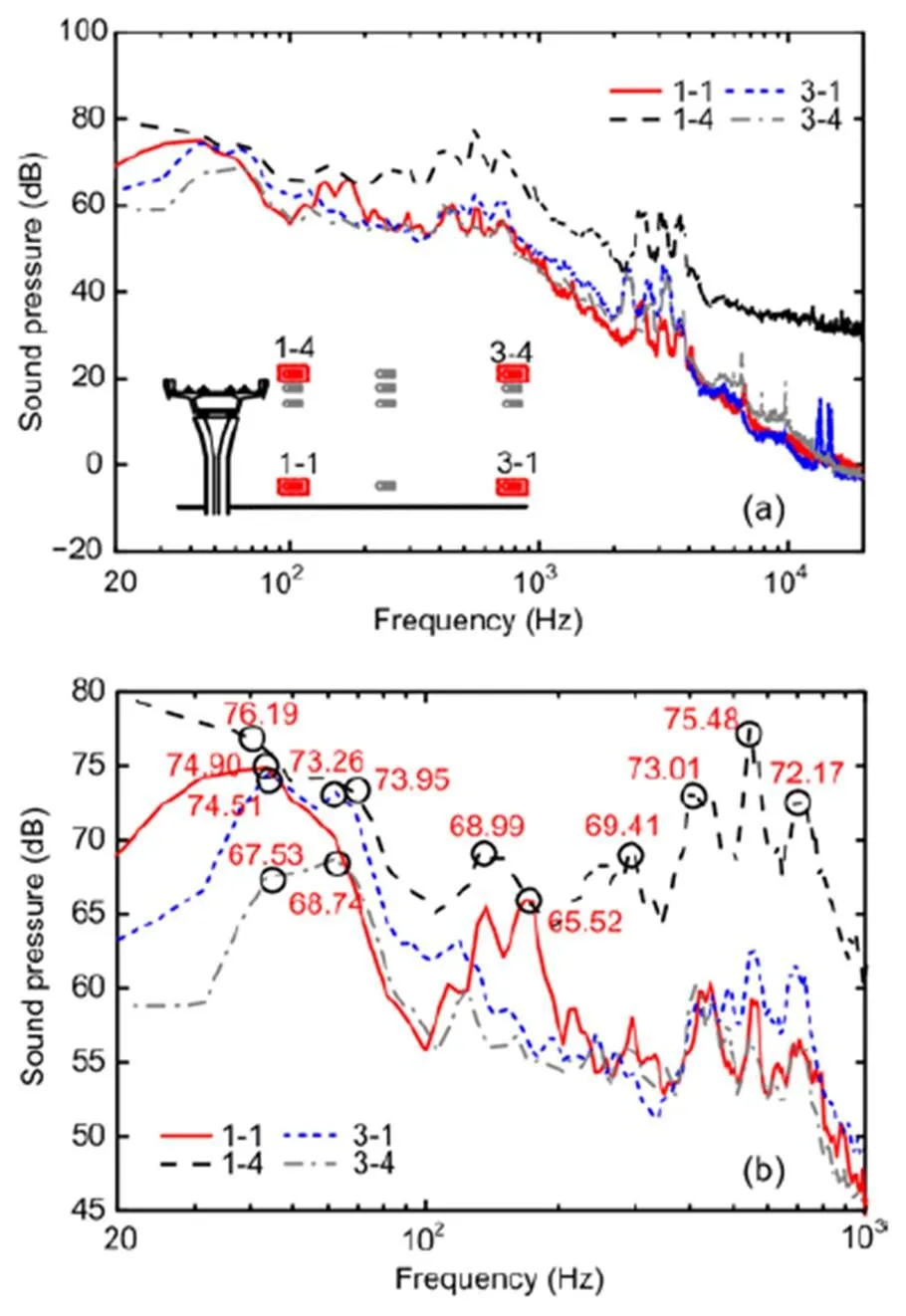
Fig. 5 Noise spectrum beside the bridge: (a) 20–20 000 Hz; (b) 20–1000 Hz

The peak values of measuring point 1-4 in the middle-high-frequency band above 250 Hz are consistent with the peak frequencies of wheel/rail noise. The corresponding frequencies are 315 Hz, 400 Hz, 500 Hz, and 800 Hz, indicating that the middle-high-frequency noise at measuring point 1-4 is caused mainly by wheel/rail noise. The noise peaks of measuring points 1-1, 3-1, and 3-4 occur in the low-frequency band below 250 Hz. At these points, the sound pressure level above 250 Hz significantly decreases, and the local peak frequency corresponds to wheel/rail noise. In the low-frequency band, local peaks occur at measuring points 1-1 and 1-4 near the bridge in 40–60 Hz and 125–160 Hz. Only local peaks occur at measuring points 3-1 and 3-4 on the far side of the bridge at 40–63 Hz.

To take specific measures to reduce the noise, the ratios of sound energy in each frequency band were analyzed at different measuring points. Based on this, the experiment data were analyzed by linear weighted one-third octave. The formula for calculating the relative ratio (η) of the sound energy of different frequency bands to the total sound energy of the measuring point is

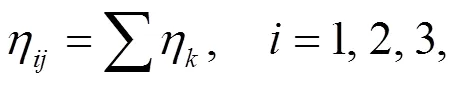
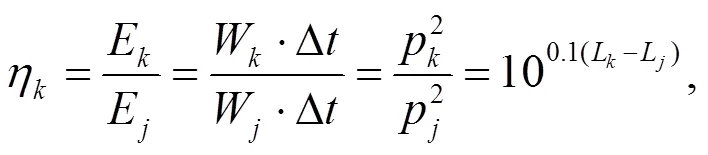
where=1, 2, and 3 represent the low-frequency band (20−250 Hz), mid-frequency band (250−400 Hz), and middle-high-frequency band (400−1000 Hz), respectively;=1, 2, 3, and 4 represent the noise measuring points beside the bridge: 1-1, 3-1, 1-4, and 3-4, respectively;represents theth central frequency of one-third octave in the frequency band.,,, andare the sound energy, sound power, sound pressure, and sound pressure level, respectively.is the time.

The total linear sound pressure level of measuring point 1-4 on the bridge side in the audible range is 88.7 dB. The sound pressure levels at the center frequency corresponding to each one-third octave and the relative ratio of noise energy to the total sound energyare shown in Fig. 6.

Taking the total sound energy of measuring point 1-4 as the reference value, the relative energy ratios of measuring points 1-1, 3-1, 1-4, and 3-4 on the bridge side in different frequency bands are shown in Fig. 7.

As can be seen from Fig. 7, the middle-high frequency of measuring point 1-4 accounts for the largest proportion (65.2%) of the reference value. The low-frequency noise energies of measuring points 1-4 and 1-1 account for 16.6% and 7.7%, respectively. The mid-frequency noise energy of measuring point 1-4 accounts for 7.6%. The noises at measuring points 3-1 and 3-4 are largely dominated by low frequencies with energies accounting for 8.9% and 3.2%, while in the mid-high frequency energy accounts for less than 3.0%.

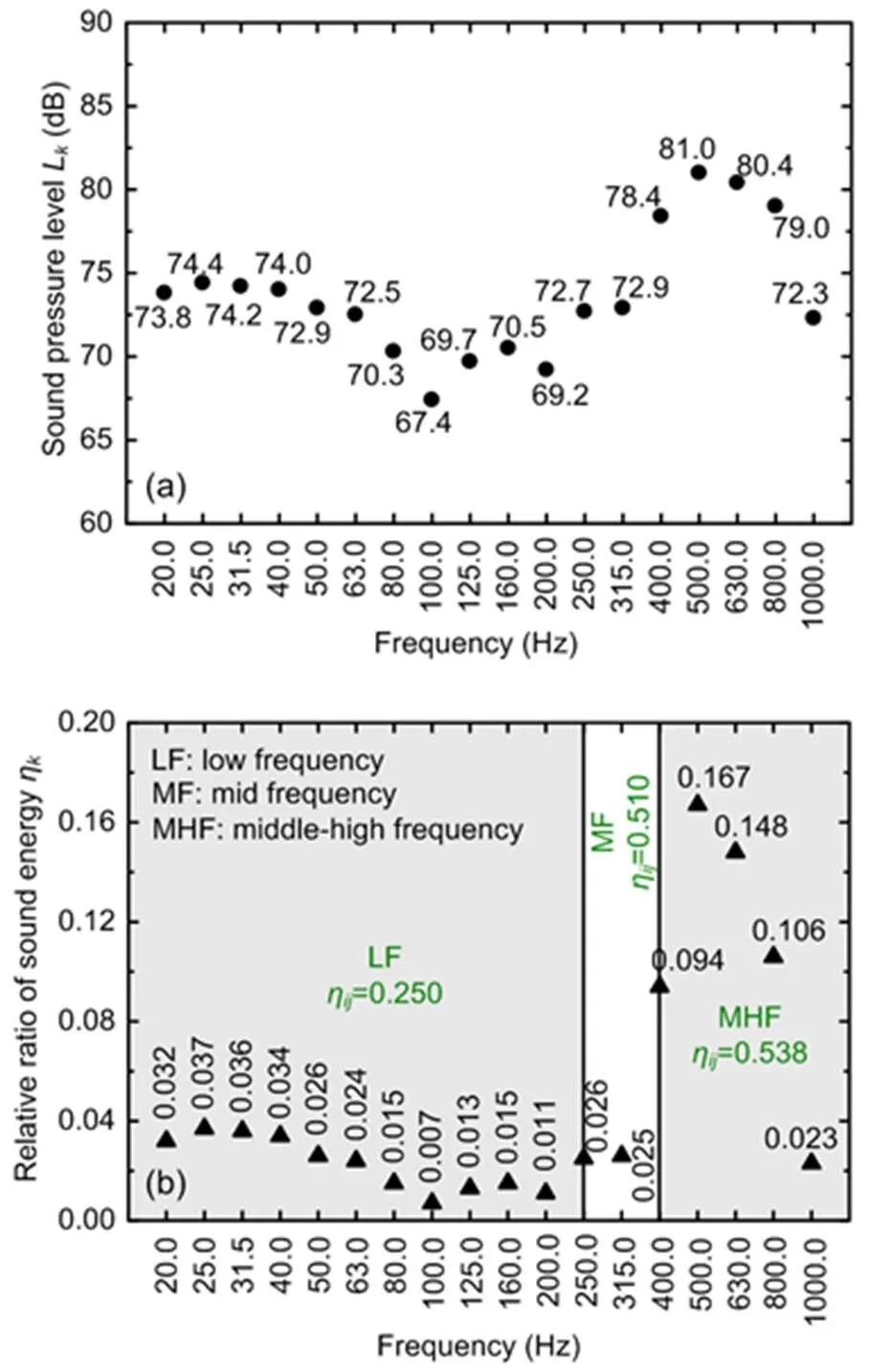
Fig. 6 Sound pressure level Lk (a) and relative ratio of sound energy ηk (b) at point 1-4

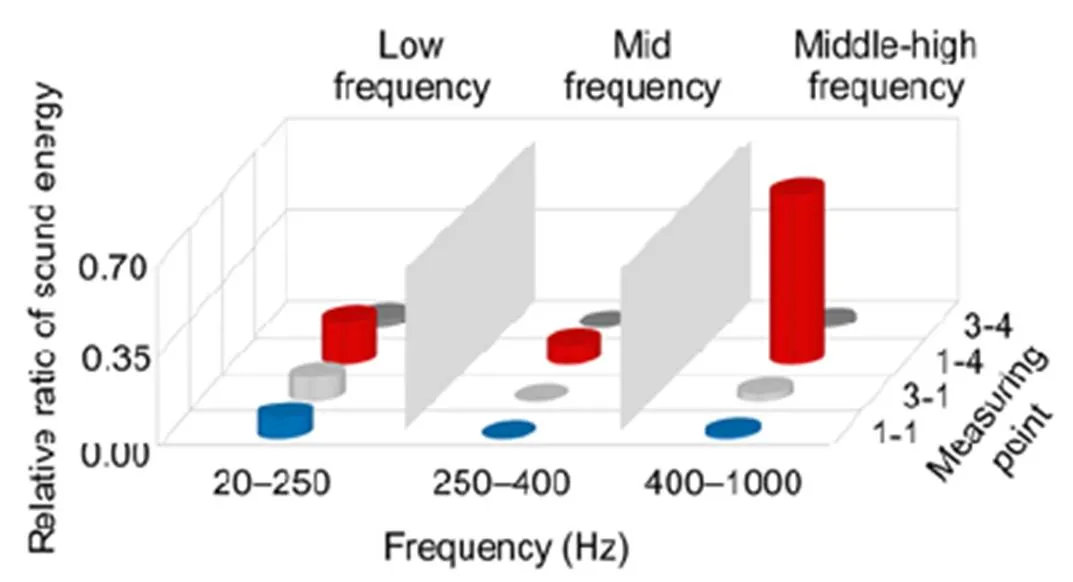
Fig. 7 Relative energy ratios of noise energy at measuring points on the bridge side in different frequency bands

3 Impact of bridge structure on noise

Based on the metro train-track-bridge (TTB) model, an acoustic radiation calculation model was built and the model validation carried out. Following this, the impact of the box girder structure on environmental noise and the corresponding acoustic contribution of different panels were calculated based on the acoustic model. Using time-domain and frequency-domain analysis methods, the impact of bridge structure on the bridge-side environmental noise was analyzed.

3.1 Metro train-track-bridge coupling model

The metro TTB interaction system was built by combining the multi-rigid-body dynamics method and the finite element method. In the dynamic model, the metro train, ballast-less track, and box girder bridge are taken as three subsystems, coupled through wheel-rail and track-bridge interaction (Zhang et al., 2019), as shown in Fig. 8.

The dynamic equations can be described as

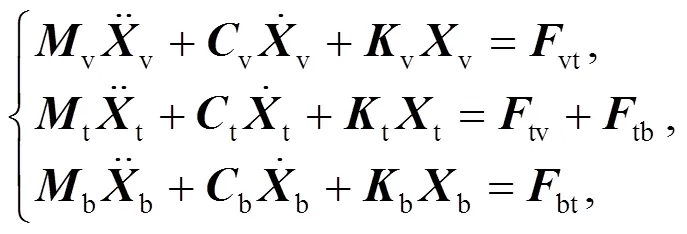
The metro train is comprised of six vehicles, and each vehicle is considered to be comprised of the rigid bodies of a car body, two bogies, and four wheelsets. There are 35 degrees of freedom (DOFs) in them, which comes to a total of 210 DOFs for the train. In addition, viscous dampers and linear springs are adopted in the primary and secondary suspension systems to build the train submodel, whose parameters are shown in Table 2.

The wheel-rail interaction force includes normal contact and tangential creep force. Normal contact force is derived by nonlinear Hertzian elastic contact theory, and tangential creep force is calculated by Kalker’s creep forces linear theory.

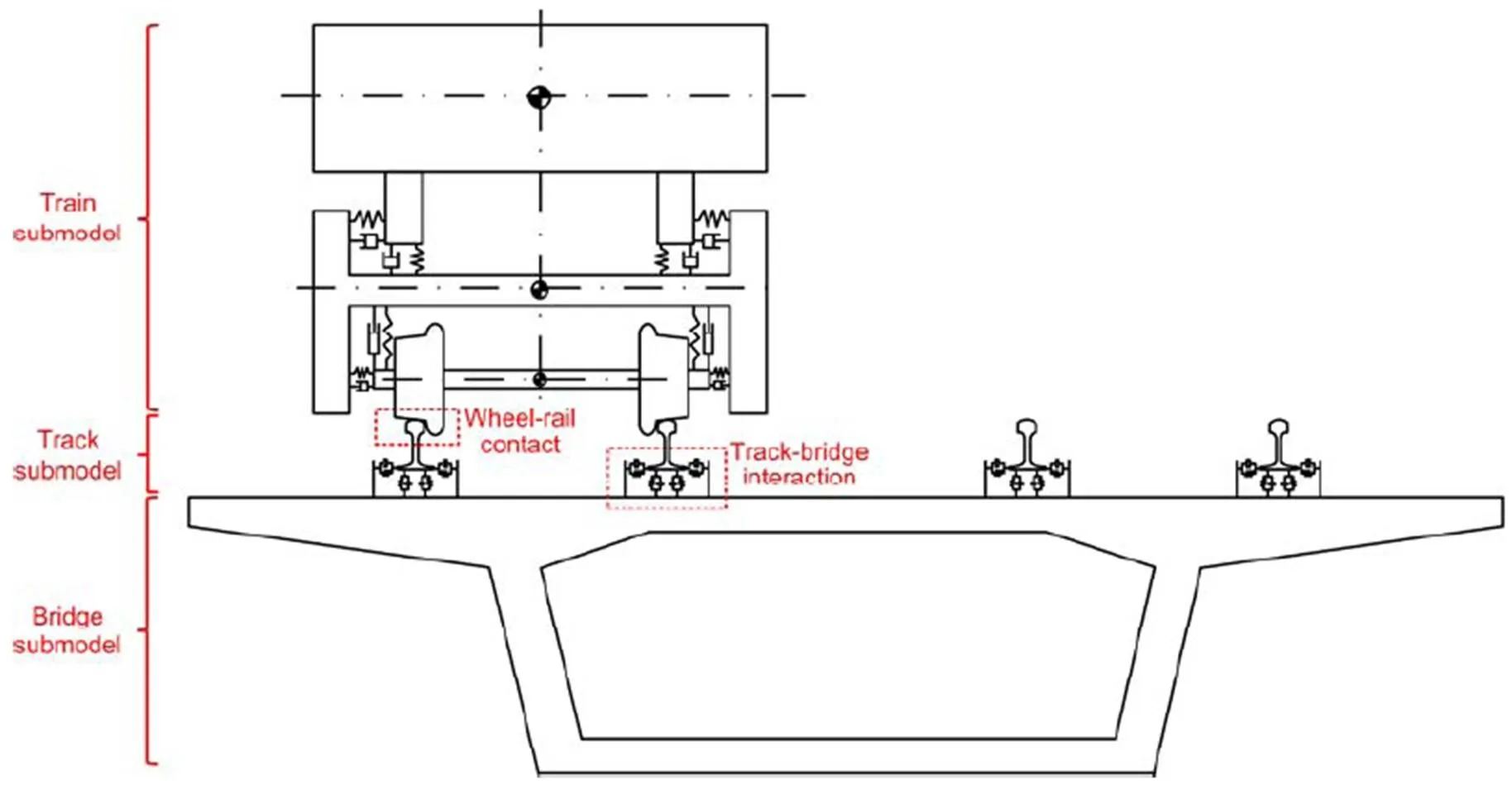
Fig. 8 Dynamic model of the TTB system

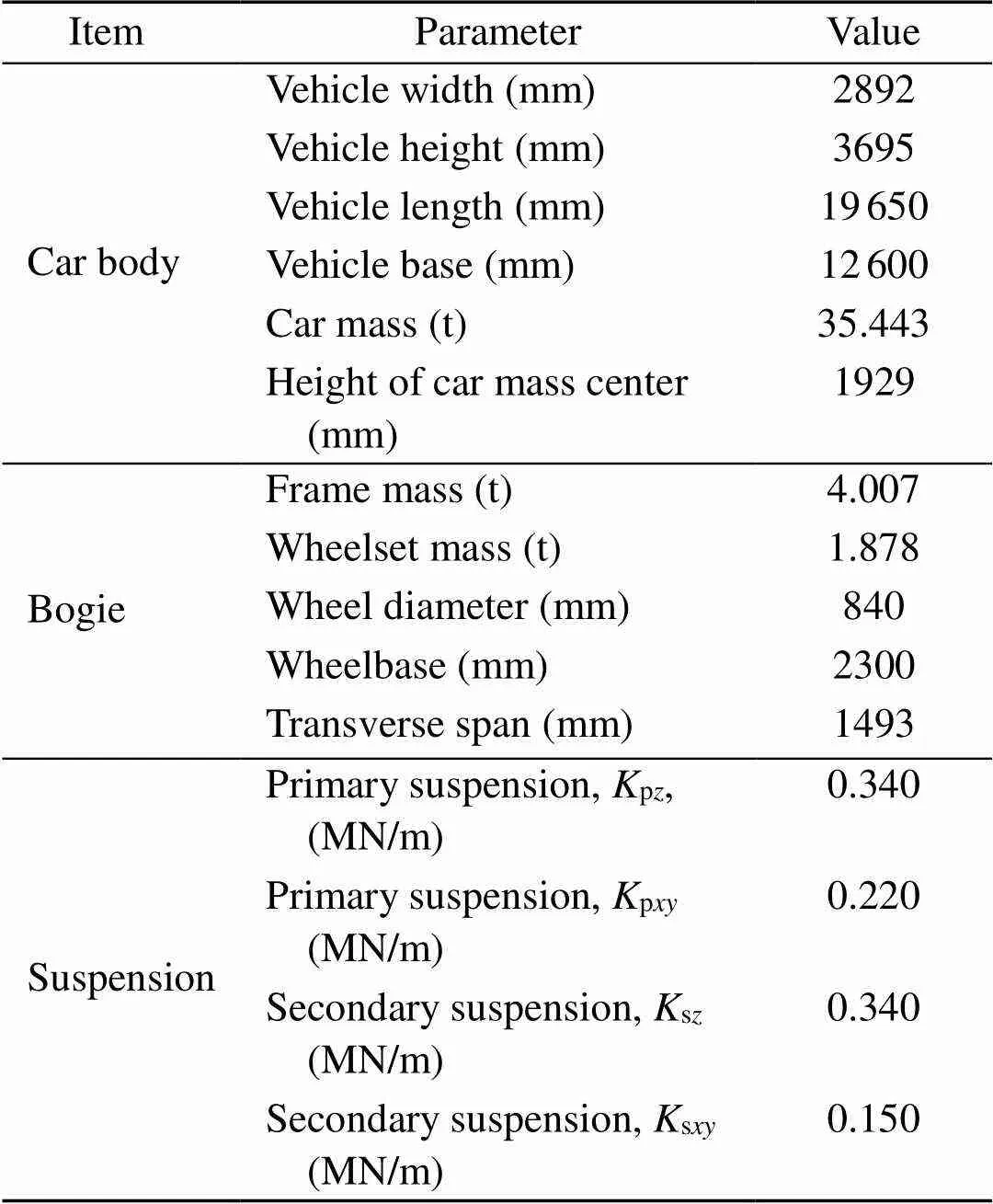
Table 2 Parameters of the metro vehicle

represents the stiffness; subscripts “p” and “s” represent the primary and secondary suspensions, respectively;,, andrepresent the longitudinal, lateral, and vertical directions, respectively

The rail is 60 kg/m which is modelled as an infinite Timoshenko beam discretely supported on fasteners. Three DOFs of the rail are taken into account: vertical, lateral, and torsional motions. The rail is connected to the track panel through a spring-damper unit with a stiffness of 30 kN/mm and damping of 80 kN·s/m, with a spacing of 0.6 m. The span of the simply-supported beam bridge is 30 m. The length of the simulated line is 90 m. The rail bearing platform is rectangular (1.56 m×0.28 m).

The elevated structures of the lines are simplified as a simply-supported double-line straight box girder bridge. The bridge is based on the finite element method, modeled with solid elements, whose damping is conceptualized in terms of Rayleigh damping. The structural dimensions of the cross section of the bridge is shown in Fig. 9.

To analyze the coupled time-varying system of TTB, the method chosen was to establish a dynamic analysis model for the train-bridge system (with the UM-ANSYS co-simulation platform), then the Park parallel numerical simulation method was used to solve this system in the time domain. Based on this, the wheel-rail forces were taken to input to ANSYS software to solve the node responses of the whole model.

Model validation was achieved by comparing simulation and measurement results. The train speed was 67.9 km/h, which is shown in Fig. 10.

Fig. 10 shows that the variation trend and values of the simulation results are concordant with those measured within 100 Hz, but when levels are greater than 120 Hz the differences are larger. This TTB coupling dynamic model is relatively simple. The train is simplified as a mass-spring-damping system. The fasteners are treated as massless spring dampers. The vibration characteristics of many vehicle parts and track parts are not reflected, resulting in the artificial filtering of high-frequency vibrations transmitted to the bridge. The simulation cannot accurately reflect high-frequency results. The peak frequency of external excitation calculated by the model is small after 100 Hz, and the impact on the vibration of the bridge structure is weakened.

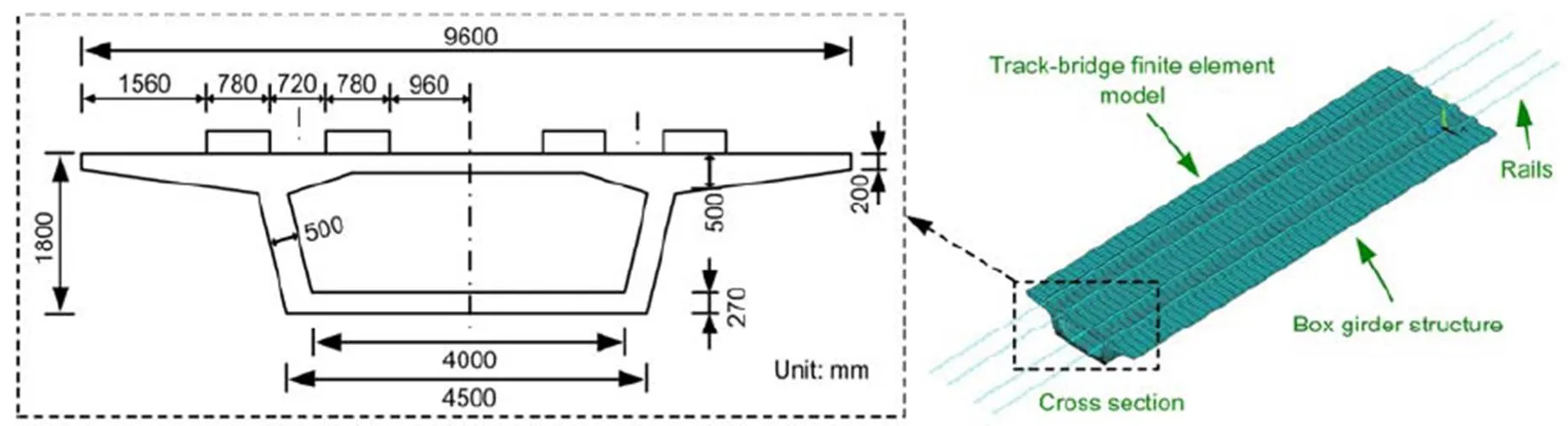
Fig. 9 Finite model and structural dimensions of the cross section of the bridge

3.2 Acoustic radiation calculation model

Based on the dynamic model, the transient boundary element acoustic model was established using LMS Virtual.Lab acoustic simulation software (Bewes et al., 2006; Sun, 2012). The sound pressure cloud chart is shown in Fig. 11.

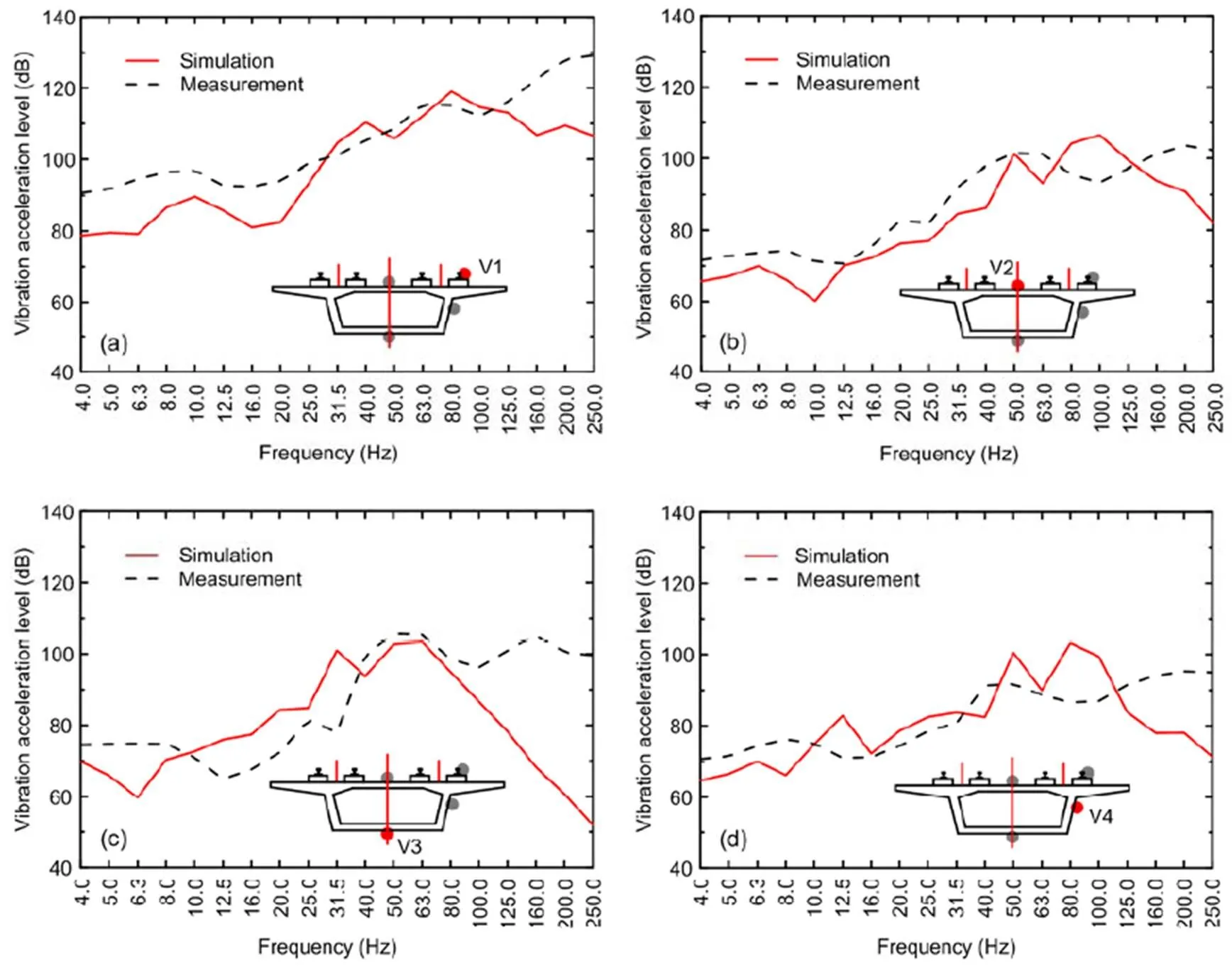
Fig. 10 Vibration comparison of the simulation and the measurement data: (a) at measuring point V1; (b) at measuring point V2; (c) at measuring point V3; (d) at measuring point V4

Fig. 11 Transient boundary element acoustic model and acoustic computing model

(a) Sound pressure cloud chart when the train initially enters the bridge; (b) Sound pressure cloud chart when the train progresses to the mid-span

Fig. 11a shows the sound pressure cloud chart when the train initially enters the bridge. Fig. 11b shows the sound pressure cloud chart when the train progresses to the mid-span. It can be seen from Fig. 11 that the noise energy attenuates to the surrounding space. As the train approaches the mid-span, the sound pressure in the mid-span increases gradually.

The time-history curve of noise at the measuring point is shown in Fig. 12.

Fig. 12 Time-history curves of noise at measuring points 1-4 (a) and 3-1 (b)

As shown in Fig. 12, the sound pressure changes dramatically with time, and the sound pressure value appears to be 50–70 dB. During the passage of the train over the viaduct, the sound pressure amplitude is relatively high, which reflects that structure-borne noise is one of the noise problems.

It is difficult for the time-history curve of sound pressure to reflect the frequency composition of sound pressure, and so the frequency spectrum analyses of the sound pressure level are compared, as shown in Fig. 13.

The sound pressure value is generally lower than the measured value. The bridge structure-borne noise is mainly concentrated in the lower frequencies. Comparing the simulation results with the test, there is a difference of approximately 10 dB between the two in some frequencies, indicating that besides bridge structure-borne noise, wheel/rail noise also contributes strongly to low-frequency noise.

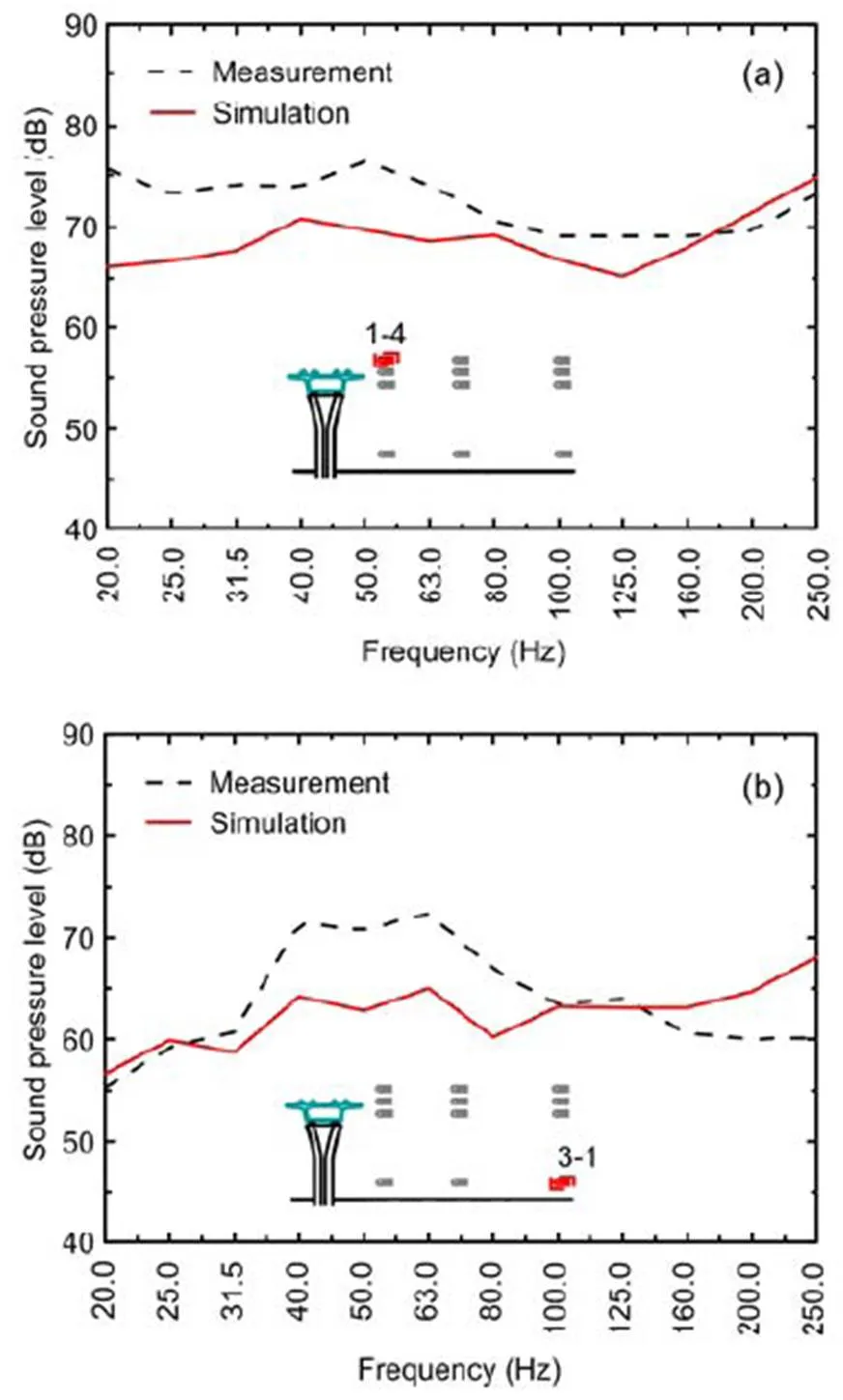
Fig. 13 Frequency spectrum analysis of noise at the measuring points 1-4 (a) and 3-1 (b)

3.3 Impact of girder structure on environmental noise

The distribution of the calculated structure-borne noise is shown in Fig. 14.

Fig. 14 shows that the frequency band of the simulated noise peak is largely 31.5–100 Hz. In general, the local peak values of the measuring points at=7.5 m appear mainly at 40 (1-3 and 1-4) and 80 Hz (1-1). The local peak values of the measuring points at=22 m appear mainly at 20, 40, and 80 Hz. The local peaks at=55 m are mainly concentrated at 20, 40, 63, and 100 Hz.

Fig. 14 Impact of girder structure on environmental noises at d=7.5 m (a),d=22 m (b), and d=55 m (c)

3.4 Acoustic contribution analysis of girder panels

The contribution of each panel of the bridge structure to the sound pressure at any position in the sound field space is different. It is necessary to conduct panel acoustic contribution analysis (PACA) for each panel before optimizing a structure (Pallas et al., 2011). The component with the greatest influence on noise is preliminarily determined. This provides a theoretical basis for noise reduction design.

When studying the noise radiation characteristics of the box girder structure, the sound wave generated by the vibration of a certain surface of the bridge is regarded as a plane sound wave. Assuming that a panel is divided intofinite elements, the total sound pressure of the external sound field is a vector superposition offinite elements.

The sound power of the box girder bridge at frequencyis

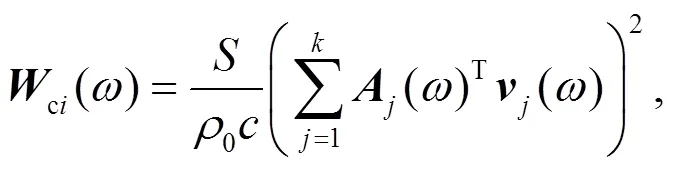
whereci() is the sound power of theth panel at frequency;cis the total sound power contributed by all panels of the bridge;is the area of the acoustic wave surface;0is the density of air;is the sound speed in air;() is the acoustic transfer vector (ATV) of elementat frequency;v() is the normal vibration velocity of elementat frequency;is the total number of panels of a bridge.

The two end faces of the box girder butt up with the adjacent box girder, which has little impact on the environmental noise, and so its calculation is not considered. The panel division diagram of the box girder boundary element model is shown in Fig. 15.

Assuming the eight panels are different sound sources, the sound pressure levels at the field points are calculated. The acoustic contribution of each panel at measuring point 3-1 at 63 Hz is shown in Fig. 16.

Fig. 16 shows that the contributions of panel-radiated noise to environmental noise are different. These results are consistent with the qualitative analysis of large vibrations of low stiffness panels.

4 Coherence analysis in consideration of the Doppler effect

To reduce the vibration and noise of the elevated line, it is necessary to analyze how the noise varies from the noise source to the environmental measuring point near the bridge. The noise generated by a train crossing a bridge is mainly divided into the pantograph area, car body area, wheel/rail area, and bridge area. Due to the low speed of urban rail transit, the noise generated in the pantograph area is relatively small. In this study two such main noise sources are analyzed as the wheel/rail noise and the structure- borne noise of the bridge.

Fig. 15 Specific positions of the bridge panel

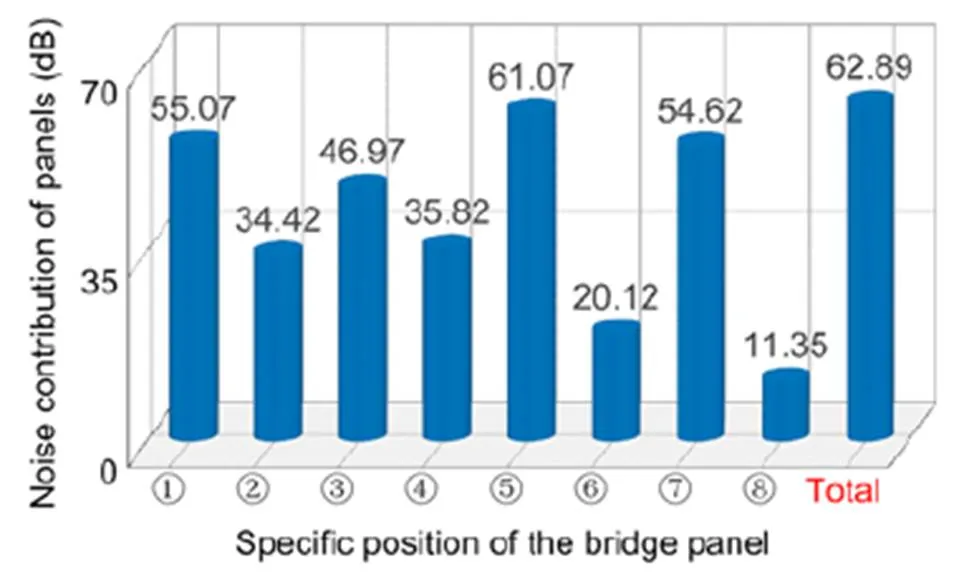
Fig. 16 Acoustic contributions of different bridge panels during train passage

4.1 Doppler effect

Because the train is moving and the noise measuring points on the bridge side are stationary, the frequency received by the noise measuring points, relative to the frequency emitted by the sound source, will shift within a certain range due to the Doppler effect. The sound pressure amplitude will also change. A diagram of the principle of the Doppler effect is shown in Fig. 17.

Suppose the noise source moves from left to right at speed;is the angle between the line of the sound source and the measuring point where the microphone is located, and the direction of travel of the train. When the sound source is approaching the sound receiving point,is less than 90o; when the sound source is moving away,is greater than 90o. The frequency of the sound source point is, and the frequency received by the sound level meter is′.

The formulas of frequency and sound pressure affected by the Doppler effect are expressed as

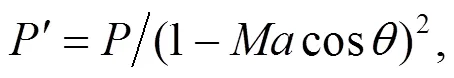
whereis the Mach number of the moving sound source,=/0;0is the propagation velocity of sound waves in the air,0=340 m/s;is the sound pressure at the sound sources;′ is the sound pressure at the receiver.

We can see that the relative motion of the source and observer causes a change in the wavelength of the object’s radiation. In front of the moving sound source, the sound wave is compressed, with shorter wavelengths and higher frequencies. The opposite effect occurs behind the source of the moving wave, i.e. the wavelength becomes longer, and the frequency becomes lower. The higher the velocity of the source, the greater the effect.

During the test, the average speed of the train is 65 km/h (18 m/s), and thus the Mach number is 0.05. The closest and farthest distances between the measuring points on the bridge side to the track centerline are 7.5 m and 55 m, respectively. According to Eqs. (6) and (7), assuming the moving train is a single-point sound source, for the measuring point 3-(=1, 2, 3, 4) of=55 m, the frequency shift influence range will be 1.04–0.96; for measuring point 1-with a horizontal distance of=7.5 m, the frequency shift influence range will be 1.06–0.95.

The noise in the area of the wheel-rail is generated by the relative movement of the wheel and rail and the operation of the equipment. The noise in this area is usually within 1 m above the rail head around the two axles. Each wheel is a strong noise source. The rail can be regarded as an equivalent cylindrical sound source.Research considering the superposition of radiated sound from different sound sources and their directivities must be rigorous. Because the rail is stationary and its acoustic radiation has 3D characteristics, there is a certain deviation between the results of using the acoustic microphone array to test the sound radiation and evaluating the contribution of the sound radiation of the rail using theoretical research. Given the complexity of this problem, in this study, the wheel-noise measuring point on the bridge (S1) is used to replace the wheel/rail noise source for analysis; the measuring points on the bottom slab (S2), the web (S3), and the flange (S4) are used to represent the noise sources of the bridge. The wheel/rail noise is modified by the Doppler effect, while the structure-borne noise of the bridge is not.

Fig. 17 Principle of the Doppler effect

4.2 Coherence analysis method considering the Doppler effect

The coherence analysis method was adopted to further analyze the noise sources of specific frequency bands in the low-frequency energy accumulation area (Li et al., 2018, 2019). As can be seen in Fig. 18, the multi-input and single-output noise testing model was established, which is suitable for partial correlation analysis of the low-frequency band (20–250 Hz). The measurements of S1, S2, S3, and S4 as a set of noise resource signals S(=1, 2, 3, 4) are ordered input, with the noise beside the bridge as the output.

The original signal in the time domain is processed and the power spectrum is estimated by fast Fourier transform (FFT). The running speed of urban rail trains is low, and the frequency change during train passing is relatively limited. Considering that the sound pressure at the center frequency of the one-third octave represents the average value in this band, specific frequencies (43, 49, 59 Hz) can be used to approximately stand for the center frequencies of the one-third octave (40, 50, 63 Hz).

The power spectrum is in the form of the unilateral spectrum,Gis the self-power spectrum of the input signal, andGis the cross-power spectrum of the input signal and the output signal. After the self-power spectrum and cross-power spectrum functions of the noise signal are given, the conditional spectrum and conditional transfer function can be obtained:

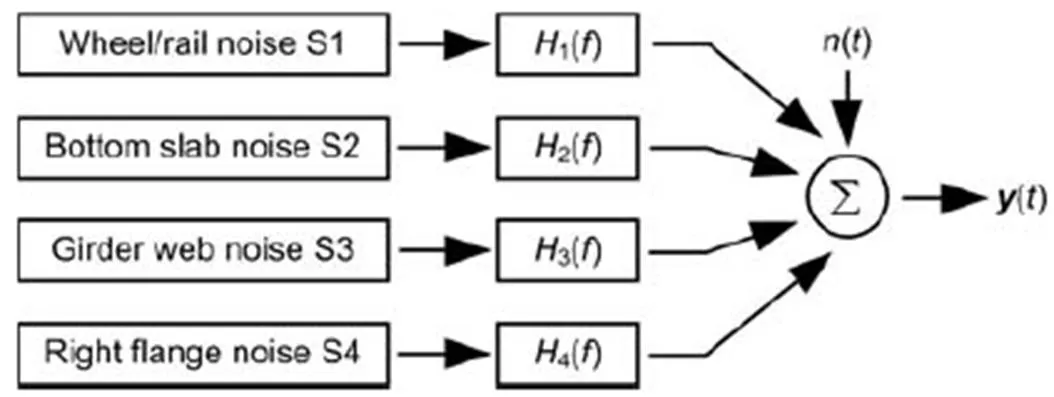
Fig. 18 Multiple-input and single-output noise model of the metro viaduct

H() is the frequency response function (FRF);() is the possible deviation from the ideal computational model

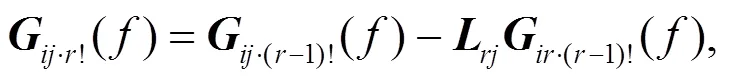
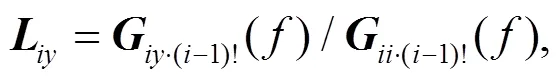
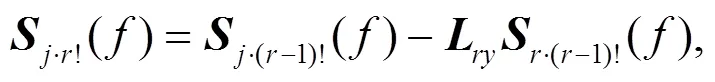
where!is the unilateral self-power spectrum of theth andth inputs after removing the influence of the firstinputs;·(r−1)!and·(r−1)!are similar to!;is the optimal conditional transfer function of theth input and output();is similar to;is the conditional transfer function of theth andth inputs;!is the conditional spectrum of theth input after removing the influence of the firstinputs.

From the definition of the coherence function, the partial coherence function (ratio of conditional cross-power spectrum and corresponding conditional self-power spectrum) is obtained. Then, the first−1 signals are removed from theth input signal, and the partial coherence function between theth input signal and the output signalin the frequency domain is

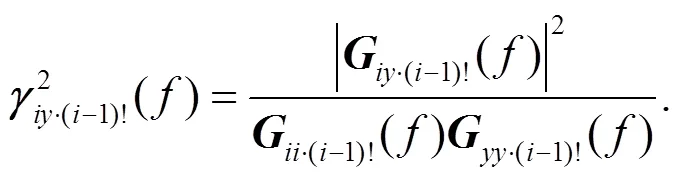
The coherence analysis flow is completed based on this, as shown in Fig. 19.

4.3 Results of coherence analysis

Fig. 20 is a self-power spectral density diagram of each noise signal on the bridge as the input.

It is clearer to draw the auto-spectrum of wheel/rail noise and bridge structure noise separately, shown in Fig. 20. The peak frequencies of the auto-power spectrum of wheel/rail noise (S1) are 20, 26, 42, 49, and 58 Hz. In the box girder structure, the peak frequencies of the bridge floor (S2), the girder web (S3), and the sail (S4) are relatively consistent, which are 43, 49, and 58 Hz. The four points have obvious superimposed peaks at the three frequencies of 43, 49, and 58 Hz.

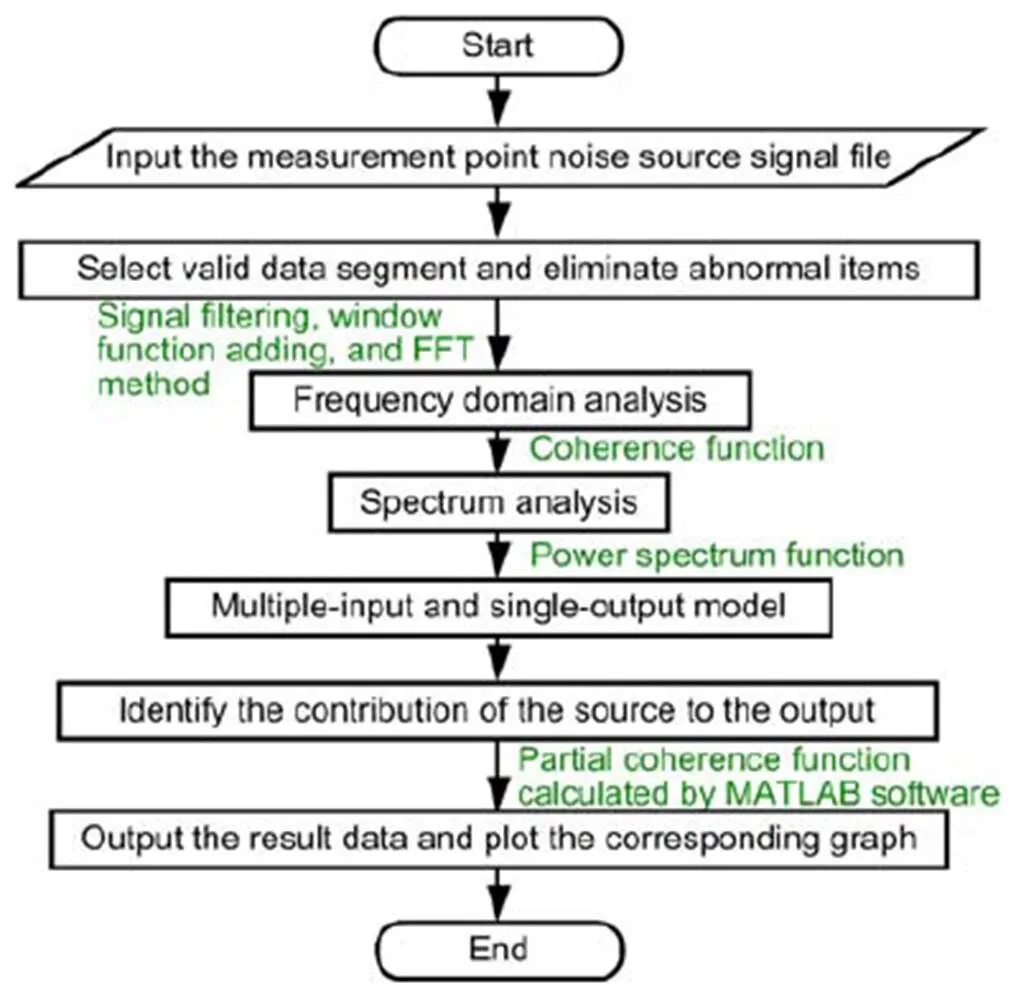
Fig. 19 Coherence analysis program

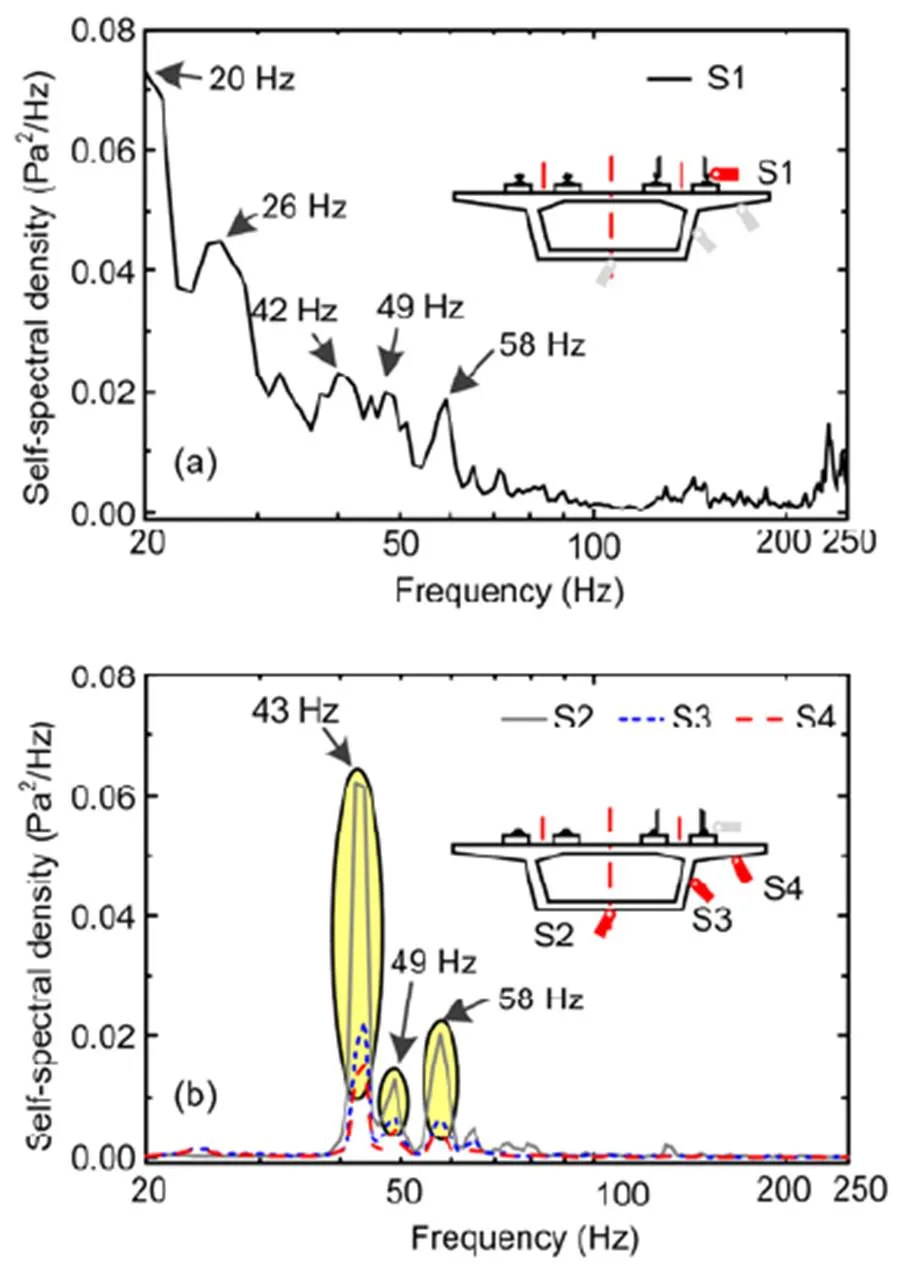
Fig. 20 Noise self-spectral density of the sensors installed: (a) wheel/rail noise; (b) box girder structural noises

To reduce errors caused by the Doppler effect, referring to the frequencies of 43, 49, and 58 Hz, the corresponding octave frequencies of 40, 50, and 63 Hz are taken as the investigated frequencies.

By changing the input order of input signals in turn, the partial coherence function values of the input noise and the output noise with different heights can be obtained by deducting the overlap between the input noise and other input noises. By comparing the partial coherence function values of different inputs and outputs, the independent contribution of each input to the output was analyzed. As an example, the partial coherence function diagram of noise signals from four noise sources on the bridge and noise signals from measuring point 1-1 beside the bridge are shown in Fig. 21.

For the remaining measuring points of 1-4, 3-1, and 3-4, the partial coherence function values of each noise source can be calculated by the same method. Major noise sources are determined by performing statistic calculations at the octave frequencies of 40, 50, and 63 Hz, as shown in Table 3.

By comparing the data in Table 3, it can be seen that the central frequencies (1/3 octave-band) of measuring point 1-1 in the acoustic shadow region are mainly composed of bridge structural noise, especially by the bottom slab (S2). The results of measuring point 1-4 are mainly made up of wheel/rail noise, while the noise of the bridge floor is a major contributor to the center frequency of 63 Hz, at which the partial coherence function value reaches 0.361.

For the environmental noise far from the elevated structure, the noise contributor for measuring points 3-1 and 3-4 at the one-third octave-band center frequencies of 40, 50, and 63 Hz is bridge structure- borne noise. Contributors according to the degrees of contribution from strong to weak are the bottom slab (S2), the right flange (S4), and the right girder web (S3).

5 Conclusions

In this study, environmental noise beside the box girder of a metro line has been analyzed. Firstly, the field measurement process was described, the noises of measuring points on the bridge deck and beside the box girder were analyzed, and the environmental noise energy distribution was completed. Based on the metro TTB model, the acoustic radiation calculation model was built, and model validation was carried out. Then, the impact of the box girder structure on environmental noise and the corresponding acoustic contributions of different panels was calculated based on the acoustic model. Finally, coherence analysis with consideration for the Doppler effect was conducted. Some conclusions can be drawn based on the above calculations:

Fig. 21 Partial correlation function between noises on the viaduct and point 1-1 beside the viaduct

Table 3 Partial coherence function values of each noise source for measuring points of 1-1, 1-4, 3-1, and 3-4 at the octave frequencies of 40, 50, and 63 Hz

1. For environmental noise on the bridge side, the frequency band above 250 Hz is mainly affected by wheel/rail noise. The peak noises of the bridge are mainly at 31.5–63 Hz. The peaks of wheel/rail noise are concentrated at 400–800 Hz. The noise intensity gradually decays from the near side of the bridge (low-frequency and middle-high-frequency energies are dominant) to the far side of the bridge (low- frequency energy is dominant) horizontally. It also decays in a vertical direction away from the noise sources. These patterns are influenced by the box girder structures.

2. The acoustic radiation calculation model based on the metro TTB model is effective. The Doppler effect plays an essential role in the measurement analysis, which has an influence of less than 6% on the frequency shift of an urban rail line with a speed of 67.9 km/h. The coherence analysis program performs well.

3. In the low-frequency band below 250 Hz, the main contributor to noise in the acoustic shadow area near the bridge and the ground is the vibration-radiated noise of the bridge, of which the contribution of the bottom panel is the most prominent. In the vicinity of a strong noise source, in addition to wheel/rail noise, the contribution of the bridge bottom panel at 63 Hz is also large. The noise in the comprehensive noise area of the far bridge is mainly caused by the structure-borne noise of the bridge, and the largest contributors of panel-radiated noise to environmental noise are the bottom slab and the bridge deck.

In further work, testing and the corresponding analysis of the fully enclosed sound barrier will be carried out.

Contributors

Li LI designed the research. Long-bo YU, Li LI, Yun-fei ZHANG, and Zhen-yu LEI processed the corresponding data. Yun-fei ZHANG wrote the first draft of the manuscript. Zhen-yu LEI and Zheng BU helped to organize the manuscript. Li LI and Yun-fei ZHANG revised and edited the final version.

Conflict of interest

Yun-fei ZHANG, Li LI, Zhen-yu LEI, Long-bo YU, and Zheng BU declare that they have no conflict of interest.

Bewes OG, Thompson DJ, Jones CJC, et al., 2006. Calculation of noise from railway bridges and viaducts: experimental validation of a rapid calculation model., 293(3-5):933-943. https://doi.org/10.1016/j.jsv.2005.12.016

Ford RAJ, Thompson DJ, 2006. Simplified contact filters in wheel/rail noise prediction., 293(3-5):807-818. https://doi.org/10.1016/j.jsv.2005.08.049

Kitagawa T, Thompson DJ, 2006. Comparison of wheel/rail noise radiation on Japanese railways using the TWINS model and microphone array measurements., 293(3-5):496-509. https://doi.org/10.1016/j.jsv.2005.08.037

Kouroussis G, Zhu SY, Olivier B, et al., 2019. Urban railway ground vibrations induced by localized defects: using dynamic vibration absorbers as a mitigation solution., 20(2):83-97.https://doi.org/10.1631/jzus.A1800651

Landström U, Åkerlund E, Kjellberg A, et al., 1995. Exposure levels, tonal components, and noise annoyance in working environments., 21(3):265- 275. https://doi.org/10.1016/0160-4120(95)00017-F

Li L, Yin TF, Zhu Q, et al., 2018. Characteristics and energies in different frequency bands of environmental noise in urban elevated rail., 18(2):120-128 (in Chinese). https://doi.org/10.19818/j.cnki.1671-1637.2018.02.013

Li L, Thompson D, Xie YS, et al., 2019. Influence of rail fastener stiffness on railway vehicle interior noise., 145:69-81. https://doi.org/10.1016/j.apacoust.2018.09.006

Li Q, Xu YL, Wu DJ, 2012. Concrete bridge-borne low-frequency noise simulation based on train-track-bridge dynamic interaction., 331(10):2457-2470. https://doi.org/10.1016/j.jsv.2011.12.031

Li Q, Song XD, Wu DJ, 2014. A 2.5-dimensional method for the prediction of structure-borne low-frequency noise from concrete rail transit bridges., 135(5):2718-2726. https://doi.org/10.1121/1.4871357

Ma XT, 2007. Investigation on Prediction and Control of Railway Wheel-rail Rolling Noise. PhD Thesis, Beijing Jiaotong University, Beijing, China (in Chinese).

Ngai KW, Ng CF, 2012. Structure-borne noise and vibration of concrete box structure and rail viaduct., 255(2):281-297. https://doi.org/10.1006/jsvi.2001.4155

Pallas MA, Lelong J, Chatagnon R, 2011. Characterisation of tram noise emission and contribution of the noise sources., 72(7):437-450. https://doi.org/10.1016/j.apacoust.2011.01.008

Remington PJ, 1976. Wheel/rail noise—Part IV: rolling noise., 46(3):419-436. https://doi.org/10.1016/0022-460X(76)90864-6

Rimell AN, Mansfield NJ, Paddan GS, 2015. Design of digital filters for frequency weightings (A and C) required for risk assessments of workers exposed to noise., 53(1):21-27. https://doi.org/10.2486/indhealth.2013-0003

Song XD, Li Q, 2018. Numerical and experimental study on noise reduction of concrete LRT bridges., 643:208-224. https://doi.org/10.1016/j.scitotenv.2018.06.179

Sun LW, 2012. Analysis of the car body sound-structure interaction and the contribution of plate based on LMS Virtual Lab., 224:158- 164. https://doi.org/10.4028/www.scientific.net/AMM.224.158

Thompson DJ, 2013. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control. Elsevier, Oxford, UK.

Thompson DJ, Jones CJC, 2000. A review of the modelling of wheel/rail noise generation., 231(3):519-536. https://doi.org/10.1006/jsvi.1999.2542

Zhang YF, Li J, Chen ZW, et al., 2019. Dynamic analysis of metro vehicle traveling on a high-pier viaduct under crosswind in Chongqing., 29(5): 299-312. https://doi.org/10.12989/was.2019.29.5.299

Zhao CY, Wang P, 2018. Minimizing noise from metro viaduct railway lines by means of elastic mats and fully closed noise barriers., 232(6):1828-1836. https://doi.org/10.1177/0954409717752200

*Project supported by the National Natural Science Foundation of China (Nos. 51408434, 11772230, and 51678446)

© Zhejiang University Press 2021

https://doi.org/10.1631/jzus.A1900678

TB532; U24

Dec. 30, 2019;

accepted July 11, 2020;

Dec. 15, 2020