循环图C(3k，k)的2-页交叉数

董晓媛，马登举

(1.南通师范高等专科学校数理系，江苏 南通 226007；2.南通大学理学院，江苏 南通 226000)

1 预备知识

研究交叉数的主要动机之一是图的交叉数在超大规模集成电路设计中的应用.国内外许多学者都研究过图的交叉数问题，但是到目前为止还没有找到能确定任意图的交叉数的算法.

图的一个平面画法是将图的顶点用平面上的不同点表示，边用简单曲线段表示，使得表示每条边的曲线不经过除他们的端点外的其他点.同时，还要求一个图的画法满足下列条件：(1)相邻的两条边不交叉；(2)两条边相交叉不多于一次；(3)两条边不相切；(4)没有3条边交于同一个顶点.在图G的所有画法中，交叉点数最少的画法所含的交叉点的数目称为图G的交叉数，记为cr(G).

一个k页书是由一条直线l和k≥1个半平面组成，使得每个半平面的边界都是直线l.将每个半平面称为页，而直线l称为书脊.一个图G在一个k页书上的画法是指将这个图的每个顶点都位于书脊上，每条边都画在同一页上.图G在一个k页书上的所有画法的交叉点数最少的画法所含的交叉点的数目称为图G的2页交叉数，记为cr2(G).由于一个2页书就可以形成一个平面，容易得到cr(G)≤cr2(G).

1987年，Chung等[1]对一类书图进行了研究.众所周知，一本书是由一个书脊和k个书页组成的，这k个书页有一个共同的边界就是书脊.把一个图嵌入到这本书中，这个图的每个顶点都位于书脊上，每条边都位于同一页上.最近，书图已经得到了广泛的研究.[3-4]现在，如果这本书有k页，并且允许边之间有交叉，那么就可以研究这个图的k-页书交叉数.1993年，Garey等[2]证明了确定图的交叉数是一个NP-完全问题.

循环图C(n，k)是这样一个图，它的顶点集为V={ui|0≤i≤n-1}，它的边集为

E={uiuj|0≤i≤n-1，0≤j≤n-1，i≡j(modk)}∪Cn(u0…un-1u0).

循环图C(n，k)的2-页交叉数cr2(C(n，k))是循环图C(n，k)的所有2-页书画法中交叉点数最少的画法所得到的交叉数.

2005年，Liu等[5]研究了一类循环图C(3k，k)的交叉数，当k≥3时，有cr(C(3k，k))=k.本文在此基础上，研究这类循环图C(3k，k)的2-页交叉数，并得到了其准确值cr2(C(3k，k))=k(k≥3).

为了更清楚地陈述后面交叉数的结果，给出Jordan曲线定理的内容如下：

Jordan曲线定理设J是平面上的一条Jordan曲线，平面的剩余部分被分成两个不相交的开集，称为J的内部和外部，分别记为IntJ和ExtJ，则连接IntJ和ExtJ的点的任何连线必在某点和J相交.其中一条Jordan曲线是指一条连续的，自身不交的，起点和终点相重合的曲线.

2 主要结论

文献[5]研究了一类循环图C(3k，k)的交叉数，得到如下结论：

引理1[5]当k≥3时，循环图C(3k，k)的交叉数为

cr(C(3k，k))=k.

定理1当k≥3时，循环图C(3k，k)的2-页交叉数为

cr2(C(3k，k))=k.

证明由引理1可知，cr(C(3k，k))=k.又因为cr2(C(3k，k))≥cr(C(3k，k))，从而得到了cr2(C(3k，k))的下界，即

cr2(C(3k，k))≥k.

由循环图C(3k，k)的定义可知，循环图C(3k，k)是由k个互不相交的3-圈

Ei={uiui+k，uiui+2k，ui+kui+2k，0≤i≤k-1}

和一个3k-圈C3k=(u0…u3k-1u0)组成的.由2-页书画法的定义可知，把一个图嵌入到这本书中，这个图的每个顶点都位于书脊上，每条边都位于同一页上.

当k=3时，给出C(9，3)的一个画法，如图1所示.

由循环图C(9，3)的定义可知，循环图C(9，3)是由3个互不相交的3-圈(u0u3u6u0)，(u1u4u7u1)，(u2u5u8u2)和一个9-圈C9=(u0…u8u0)组成的.为了减少交叉的点数，把顶点的顺序进行调整.

首先按照3-圈的顶点顺序把顶点分成3组

{u0，u3，u6}，{u1，u4，u7}，{u2，u5，u8}.

然后对每组的顶点进行组内微调，当每组下标最大的点在中间，每两组交界处的顶点下标相连时，可以尽量减少交叉点的个数.从而得到一种循环图C(9，3)的2-页书的画法，它的顶点顺序为

{u3，u6，u0，u1，u7，u4，u5，u8，u2}.

显然cr2(C(9，3))≤3.又因为

cr2(C(9，3))≥cr(C(9，3))，cr(C(9，3))=3，

所以cr2(C(9，3))=3.

当k=4时，给出C(12，4)的一个画法，如图2所示.

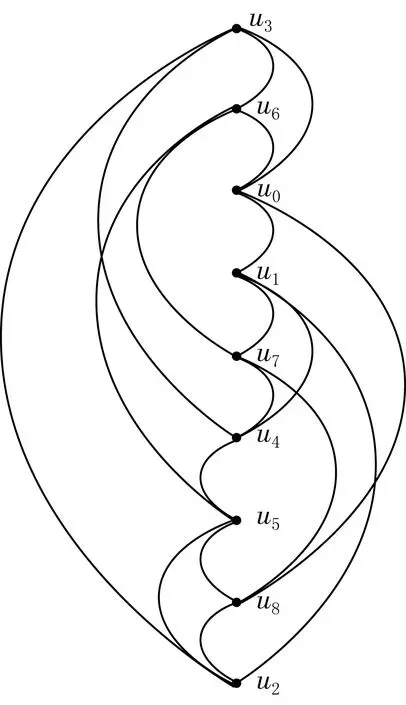
图1 循环图C(9，3)的一种2-页书的画法

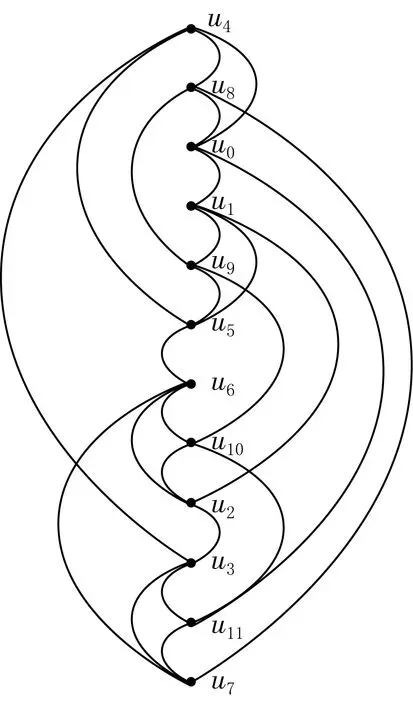
图2 循环图C(12，4)的一种2-页书的画法

由循环图C(12，4)的定义可知，循环图C(12，4)是由4个互不相交的3-圈(u0u4u8u0)，(u1u5u9u1)，(u2u6u10u2)，(u3u7u11u3)和一个12-圈C12=(u0…u11u0)组成的.为了减少交叉的点数，把顶点的顺序进行调整.

首先按照3-圈的顶点顺序把顶点分成4组

{u0，u4，u8}，{u1，u5，u9}，{u2，u6，u10}，{u3，u7，u11}.

然后对每组的顶点进行组内微调，当每组下标最大的点在中间，每两组交界处的顶点下标相连时，可以尽量减少交叉点的个数.从而得到一种循环图C(12，4)的2-页书的画法，它的顶点顺序为

{u4，u8，u0，u1，u9，u5，u6，u10，u2，u3，u11，u7}.

显然cr2(C(12，4))≤4.又因为

cr2(C(12，4))≥cr(C(12，4))，cr(C(12，4))=4，

所以cr2(C(12，4))=4.

下面给出C(3k，k)的一个画法.

当k为奇数时.由循环图C(3k，k)的定义可知，循环图C(3k，k)是由k个互不相交的3-圈Ei={uiui+k，uiui+2k，ui+kui+2k，0≤i≤k-1}，和一个3k-圈C3k=(u0…u3k-1u0)组成的.由2-页书画法的定义可知，把一个图嵌入到这本书中，这个图的每个顶点都位于书脊上，每条边都位于同一页上.为了减少交叉的点数，同样把顶点的顺序进行调整.

首先按照3-圈的顶点顺序把顶点分成k组

{ui，ui+k，ui+2k}，i=0，1，2，…，k-1.

然后对每组的顶点进行组内微调，可以发现，当每组下标最大的点在中间，每两组交界处的顶点下标相连时，可以尽量减少交叉点的个数.从而得到一种循环图C(3k，k)的2-页书的画法，它的顶点顺序为

{uk，u2k，u0，u1，u2k+1，uk+1，uk+2，u2k+2，u2，u3，u2k+3，uk+3，…，uk-2，u3k-2，u2k-2，u2k-1，u3k-1，uk-1}.

先给出3k-圈C3k=(u0…u3k-1u0)的一个画法，如图3所示，u2k-1u2k与ukuk+1产生一个交叉点，uk-2uk-1与u3k-1u0产生一个交叉点，共产生2个交叉点.

再分别画出k个3-圈，如图4所示.第一个3-圈E0={u0uk，u0u2k，uku2k}与3k-圈的边没有产生交叉点.接下来的k-2个3-圈，每个圈与3k-圈的边都产生一个交叉点，最后一个3-圈Ek={uk-1u2k-1，u2k-1u3k-1，uk-1u3k-1}与3k-圈的边没有产生交叉点.

综上，共产生了k个交叉点.从而得到cr2(C(3k，k))的一个上界：当k≥3时，cr2(C(3k，k))≤k.

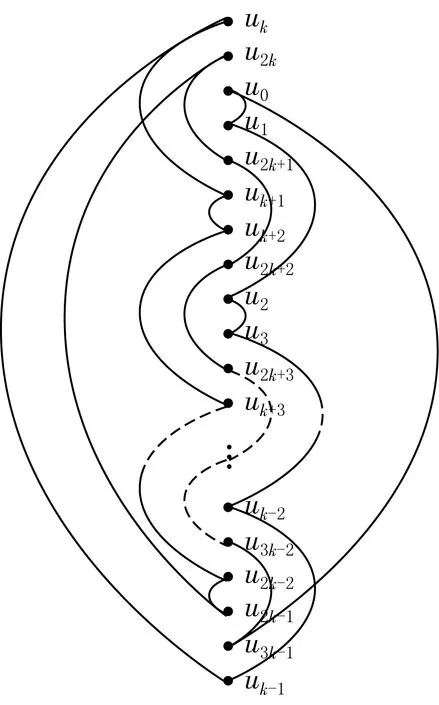
图3 k为奇数时，C(3k，k)的2-页书画法(部分)

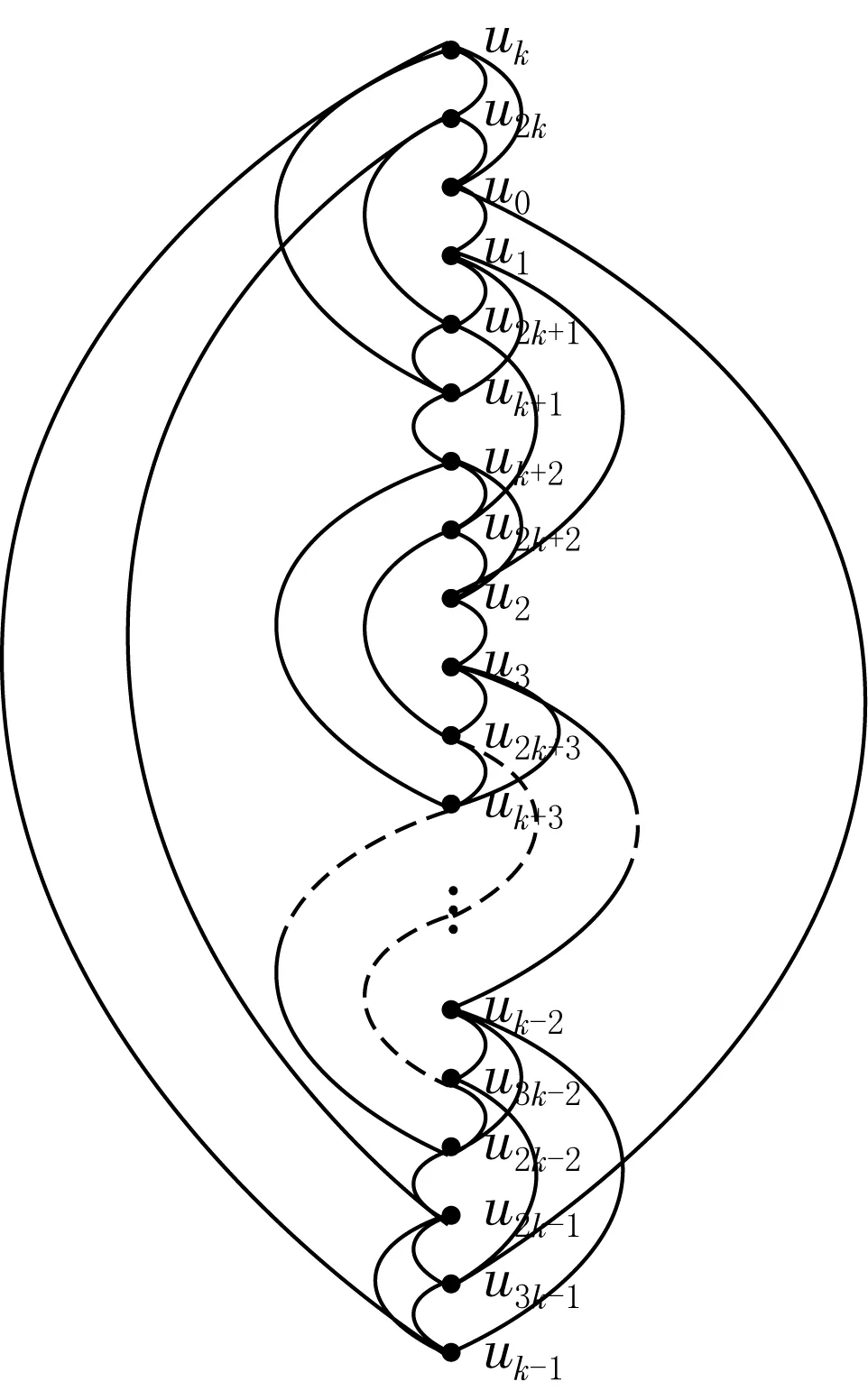
图4 k为奇数时，C(3k，k)的2-页书画法

图5 k为偶数时，C(3k，k)的2-页书画法

当k为偶数时.顶点与k为奇数时稍有差距，同样把顶点的顺序进行调整.

首先按照3-圈的顶点顺序把顶点分成k组

{ui，ui+k，ui+2k}，i=0，1，2，…，k-1.

然后对每组的顶点进行组内微调，当每组下标最大的点在中间，每两组交界处的顶点下标相连时，可以尽量减少交叉点的个数.从而得到一种循环图C(3k，k)的2-页书的画法，它的顶点顺序为

{uk，u2k，u0，u1，u2k+1，uk+1，uk+2，u2k+2，u2，u3，u2k+3，uk+3，…，u2k-2，u3k-2，uk-2，uk-1，u3k-1，u2k-1}.

类似的方法，可得到它的一个上界cr2(C(3k，k))≤k.如图5所示.

通过以上分析不难发现，不论k是奇数还是偶数，循环图C(3k，k)的2-页交叉数都为cr2(C(3k，k))=k.故当k≥3时，循环图C(3k，k)的2-页交叉数cr2(C(3k，k))=k.