教育水平与代际流动的关系——一项数理社会学的研究

□ 张云武

内容提要 本文以数理模型公式化的形式，明确了教育水平与代际流动的关系。为了推导出不依赖于特定数值的一般性命题，采用了模型由2 维度（教育水平与出身阶层）2 等级（高和低）的要素构成以及教育水平高者优先流入到精英阶层的假设。将精英阶层的选拔机制设定为注重出身阶层的词典式次序模型和注重教育水平的教育至上模型。通过比较分析两个模型，明确了三个问题：（1）教育水平的提升导致代际上升流动的封闭性这一悖论现象的产生条件；（2）教育机会均等化与代际上升流动的关系；（3）根据模型的理论值，推导出相关的理论命题。 最后， 本文验证了模型的理论值与问卷数据获得的经验值的匹配度以及指出了今后需要研究的课题。

一、研究背景与研究问题

职业阶层流动的研究中， 教育水平与代际流动的关系是一个重要的研究课题。对此，研究发现可以归纳为以下四点。

其一，如钟登（Zhong Deng）和崔曼（D.J.Treiman）所说：“在现代社会，教育是社会流动的动力机制”（Zhong Deng and Donald.J.Treiman，1997：391）。 在阶层结构开放的社会， 教育水平与职业地位存在显著的正向关系。具体而言，如果低职业阶层出身者的教育水平提高，那么该群体中，从事社会威望高、收入高的职业的个体就会增多，代际间职业阶层的上升流动就会增加， 职业阶层结构的封闭性就会弱化。 在学术界，多数学者持这一观点。

20 世纪60年代末， 美国已进入到后工业化社会。 布劳、邓肯的职业地位实现模型显示：在此期间，父亲的教育程度、子女的教育程度以及子女目前的职业地位呈现显著的正向关系， 前两者的路径系数为0.31， 而后两者的路径系数为0.39（Blau and Duncan，1967：131-140）。浜田宏研究发现：在日本，父亲为专业技术职业、管理职业等社会威望与收入高的家庭中，子女接受大学本科、研究生等高等教育机会的比例， 显著地高于父亲为其他职业的家庭的子女（浜田，2008：608）。

我国自1978年改革开放以来，工业化水平逐年提升， 可以说目前我国正处于工业化社会向着后工业化社会的转型期。国家统计局的数据显示：1978年以来，无论男性与女性，也无论出身于怎样职业阶层的家庭， 拥有大专及以上教育水平的人数比例均有很大程度的提升 （国家统计局，2015）。 在此背景下，国内学者分析了我国的教育水平与代际流动的关系。 其中，陆学艺研究发现：在我国，父亲的教育水平、本人的教育水平、本人初职地位和现职地位存在显著的正向关系（陆学艺，2004：187-197）。 比如：在1992-2001年间，父亲的教育水平对于本人教育地位获得的影响系数为0.2211（P＜0.001），而中专以上的教育水平对于本人现职地位的影响系数为0.2376（P＜0.001）。 许欣 欣 研 究 发 现：1990年18-34 岁、50 岁 以 上 和1993年18-34 岁、35-49 岁、50 岁以上的不同年龄层以及1990年和1993年全国、城镇和农村中，父亲的教育水平、 本人的教育水平和本人现职地位的关系，无论1990年还是1993年，三者均存在显著的正向关系（许欣欣，2000：288-295）。 比如：1990年50 岁以上的年龄层中， 父亲的教育水平对于本人教育水平的影响系数为0.13， 而本人教育水平对于本人现职地位的影响系数为0.27；1990年全国范围内，父亲的教育水平对于本人教育水平的影响系数为0.10， 而本人教育水平对于本人现职地位的影响系数为0.20。

其二， 作为后致性因素的教育水平对于阶层地位改善的作用出现弱化趋势 （吕效华、 吴炜，2013：15；解雨巷、解垩，2019：51-52）。 这无疑说明：职业阶层低者的向上流动呈现受阻的趋向，社会资源向着上层聚敛， 阶层固化的现象已经初步显现。

其三， 教育水平的提升与代际流动的开放性不具有显著的相关性。 早在20 世纪60-70年代，欧美学者的研究就发现： 教育水平对于代际流动并没有显著影响 （Boudon，1973：66-67；Anderson，1961：164-179）。 在我国的现阶段，也存在同样的问题。 莫艳清、 杨建华研究发现： 在我国，1978-2011年间父亲的教育水平对于本人的初职地位和现职地位并不产生显著影响（莫艳清、杨建华，2013：198-199）。

其四， 教育水平与代际流动的关系并非固定不变。 佐藤俊樹的分析就发现：在日本，被认为拥有高等教育水平， 且从事专业技术职业与管理职业的精英阶层， 在1985年以前一直呈现下降趋势，但是其后却呈现上升之势（转引自浜田，2008：609）。 在我国，中国综合社会调查（CGSS）的数据显示：近10年来，教育水平对职业阶层流动的影响呈现非线性的状态，高中及以下的人群中，教育水平的提升会导致职业流动的频率增加， 而高中及以上的人群中， 教育水平的提升反而会导致职业流动的频率下降。

上述研究发现说明：虽然在理论层面，教育水平的提升有助于代际间职业阶层的上升流动，但在现实社会，却不尽然，两者的关系复杂多变。 为了分析简便，本文将专业技术职业、管理职业的人群称为精英阶层， 而将其以外职业的人群称为草根阶层。 中国综合社会调查（CGSS）的数据显示：在我国，精英阶层的再生产在2010年以前呈现增加之势， 而其后则呈现一定的减少之势。 也就是说， 由于草根阶层出身者的教育水平提升，2010年以后草根阶层的代际向上流动现象增加。因此，在某种条件下， 教育水平的提升对于代际上升流动的正向影响并非保持不变。 上述中国综合社会调查的分析以及国内外学者的研究发现， 就充分说明了这一点。其产生原因是：随着经济的快速发展，居民的教育水平不断提升，可以进入到精英阶层选拔体系的范围扩大， 从而导致职业阶层结构的开放性提高， 但是由于阶层的选拔体系逐渐饱和， 本来处于阶层位置高端的精英阶层的再生产再次显现出来。大学学历者越多，则适合其从事的职业越少，在此现实下，大学学历者也不得不从事非大学学历者从事的职业。但是，这并不能够成为解释精英阶层的代际流动的开放性或者封闭性的原因。比如：精英阶层与草根阶层的教育水平同时提升的话， 精英阶层出身的教育水平高者流入到草根阶层的比例必然会适当增加。 该现象的产生将会弱化精英阶层的再生产。

本文的数据均来自于中国综合社会调查（Chinese General Social Survey，CGSS）2010—2019年的数据，因此数据具有相当的可靠性。图1 表示的是： 根据2010-2019年问卷数据的统计结果，用优势比exp（β）表示的、作为精英阶层的父亲的教育水平（大学本科及以上）对于本人现职地位的影响。 可以发现：虽然父亲的教育水平对于本人现职地位大多具有正向影响（exp（β）＞0），但教育水平的提升与代际流动的关系并不是永恒不变的，而是因年代呈现不同的变化倾向。 具体而言，随着年代的推移，作为精英阶层的父亲的教育水平对于本人现职地位的正向影响， 在2010-2012年间，呈现愈发显著之势，在2013-2015年间，正向影响的程度却没有显著的变化，而2016-2019年间，正向影响又呈现显著的弱化态势。

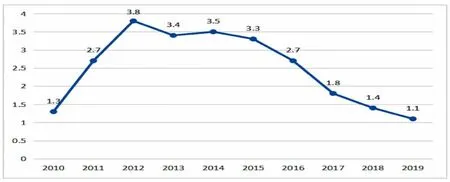
图1 2010-2019年精英阶层的父亲教育水平对本人现职地位影响的优势比exp（β）

近些年， 阶层流动的不平等引起国内学界的关注。关注的问题主要有两点：（1）事实确认，即阶层流动的不平等是否已经真的产生；（2）价值判断，即若阶层流动的不平等已经产生， 从社会规范的观点看，是否处于可容许、可接纳的范围内。 但是综观已有研究，在怎样的机制下产生的阶层流动的不平等？该问题研究得还不够细致。基于该背景，本文拟从数理社会学的视角重点研究上述问题。

在数理社会学领域，布登（R.Boudon）通过数值模拟方法对教育水平的提升与代际流动的开放性与封闭性的复杂关系进行了分析（Boudon，1973：66-67）。 布登的数值模拟分为IEO（Inequality of Educational Opportunity）和ISO（Inequality of Social Opportunity）两个模型，前者指“教育机会的不平等”，后者指“社会机会的不平等（代际流动的不平等）”。根据ISO 模型，布登推导出了教育机会的均等化未必能够显著地弱化阶层流动的不平等。但是，该命题毕竟是基于数值模拟获得的计算结果，且依照设定的参数获得的有限结论，因此仅仅属于常识性的理论命题。 为了更为准确地明确教育水平的提升与代际流动的关系， 无疑需要更为一般性的数学模型。

基于上述分析，本文将ISO 模型产生的数据模拟一般化，以更加钝化的形式，将阶层的选拔体系饱和作为数理模型进行公式化，明确在怎样的条件下，教育水平的提升能够提升代际流动的封闭性。

二、词典式次序模型

所谓词典式次序， 是指次序特别恰当适用和条理清晰无误的一种排序方式。 本部分将布登的ISO 模型简洁化与一般化， 将教育水平和代际流动的关系模型公式化， 为清晰地把握两者的关系进行预备性分析。 为了能够推导出不依赖于特定数值的一般性结论，模型采用比较简单的假设，即由两个维度（教育水平与出身阶层）两个等级（高和低）的因素构成，根据教育水平和出身阶层的词典式次序，决定进入到精英阶层的优先顺序。

（一）词典式次序模型的假设

假设1.根据职业与经济地位，可将出身阶层分为两大类别，即精英阶层出身与草根阶层出身，两者分别用J 和C 表示（J、C 仅为符号，无特别含义。 以下所用的符号均相同）。 将社会全体成员中的精英阶层比例和草根阶层比例分别设定为b 和1-b。 该比例在代际间是不变的。

假设2.精英阶层和草根阶层的教育水平分别设定为j 和c。 教育水平分为高等教育和低等教育，分别用G 和D 表示。

假设3.能够进入到精英阶层的优先权，由两个维度的词典式次序赋予。 两个维度分别指教育水平和出身阶层。

以上的假设也许过于简单，但是本文认为：由于教育水平与代际流动概率的关系非常复杂，因此为了从其关系中提炼出最为核心的演变机制，与复杂的假设相比，简单的假设反而更适用。阶层与教育水平的等级数量减少， 更能够对应于数据层面的阶层与教育水平的定义。一般情况下，大学教育水平为主要参数，因此可设定为两个等级，即大学毕业和非大学毕业。 上述假设3 的本质意义可做两种解释：其一，可解释为精英阶层出身者建构的关系（社会资本）更为有利；其二，可解释为布迪厄提出的文化资本更为有利。无论哪一种解释，重要的是， 均表现出了阶层选拔机制不健全的教育至上社会。

1.阶层标签与精英阶层流入率

将表示教育水平与阶层位置组合的GJ、GC、DG、DC 称为阶层标签。 标签通常以教育水平和出身阶层的高低表示。将B（f）定义为“阶层标签为f，且到达精英阶层的人数在整个社会的比率（精英阶层流入率）”。 也就是说，如果将U=阶层标签为f、Q=到达阶层为精英阶层的话，则B（f）= Pr（U∩Q）。 另外还表示，P（f）是阶层标签f 在整个社会中人数的比例。

根据词典式次序模型的假设， 能够到达精英阶层的优先顺序依次是： 教育水平高且精英阶层出身（GJ）、教育水平高且草根阶层出身（GC）、教育水平低且精英阶层出身（DJ）、教育水平低且草根阶层出身 （DC）。 各个阶层的人口比例的计算式，如下面的计算式（1）所示，而代际流动的流程，如图2 所示。

计算式（1）：P（GJ）=bj，P（DJ）=b（1-j），P（GC）=（1-b）c，P（DC）=（1-b）（1-c）

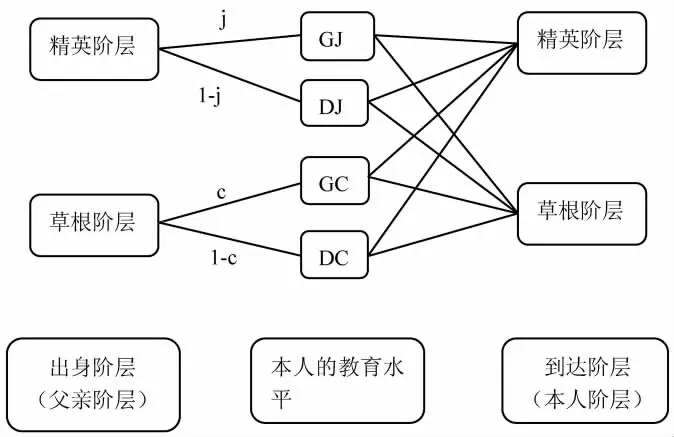
图2 代际间流动的流程

从图2 中可见，本人到达怎样的阶层，受本人的出身阶层和受教育水平的影响。 虽然出身于精英阶层，但未必能够到达精英阶层；同样虽然出身于草根阶层，也未必就一定沉淀于草根阶层。

2.代际上升流动率

草根阶层出身者到达精英阶层的概率称为代际上升流动概率，用符号L 表示，即L=B（GC）+B（DC）。

（二）词典式次序模型的基本性质

以下表示的模型结果， 由不考虑时间因素的比较静态模型导出。

情境1：从DC 流入到精英阶层的概率，与教育水平无关，通常为0。

证明：在B（GJ）+B（GC）=b 的现实下，因为没有阶层位置的空缺， 因此DC 不能够流入到精英阶层，而在B（GJ）+B（GC）＜b 的现实下，DJ 占据着空缺的阶层位置。但是，由于此种现实下P（GJ）+P（GC）=b，必然导致B（GJ）+B（GC）+B（DJ）=b，因此无论怎样的现实，DC 均不能够流入到精英阶层。故代际上升流动概率L 仅可考虑为B（GC）。

命题1：代际上升流动概率L，如模型1 所示。

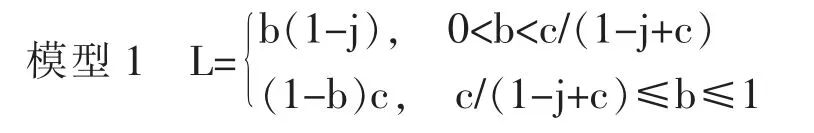
证明：根据词典式次序模型的假设，首先能够进入到精英阶层的阶层是GJ。 此时，由GJ 阶层产生的精英阶层流入率B（GJ）=（jb）。 其次能够优先流入到精英阶层的阶层是DJ。由DJ 阶层产生的精英阶层流入率B（DJ）等于精英阶层的空缺比例和S（GC）的最小值，因此形成如下公式，即B（GC）=min{b（1-j），（1-b）c}。 其中，b（1-j）为精英阶层的空缺比例，（1-b）c 为GC 阶层的比例。 因为b（1-j）＜（1-b）c⇔b＜c/（1-j+c），因此进而形成下面的模型2。

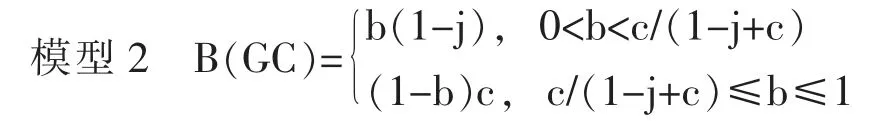
根据情境1， 该模型等于整个社会的代际上升流动概率。

命题1 的含义可作如下解释， 即精英阶层与草根阶层的教育水平没有因时间而变化时， 在精英阶层的比例很低的社会（b＜c/（1-j+c）），阶层结构的变化（精英阶层比例b 的提升）将会提高上升流动概率L。 根据命题1，L 的最大值为c （1-j）/（1-j+c），因此草根阶层的教育水平c 上升，则最大值也随之上升。 另外，精英阶层的教育水平j 的上升将会降低上升流动概率L。 另一方面，在精英阶层比例高的社会（b＞c/（1-j+c）），草根阶层教育水平c 的提升将会提高上升流动概率L。 阶层结构的变化（精英阶层比例b 的提升）将会降低上升流动概率L。另外，若精英阶层的教育水平j 提高，上升流动概率L 的最大值将会降低。

（三）教育水平因时间而变化的情境

现实社会中，一般情况下，教育水平会随着时间而发生变化。 时间s 的一元线性函数的计算式，如下面的计算式（2）所示。

计算式（2）：j=j0+αs（0≤s≤（1-j0）/α）；c=c0+βs（0≤s≤（1-c0）/β）

计算式中，j0＞0、c0＞0 为初期的教育水平，α、β分别是决定教育水平提升与降低的参数。比如：在现实层面， 教育水平一般会随着时间的推移而呈上升趋势， 因此为了很好表示其倾向， 可以假定α＞0 和β＞0。

命题2： 由草根阶层产生的上升流动概率L，如下面的模型3 所示。

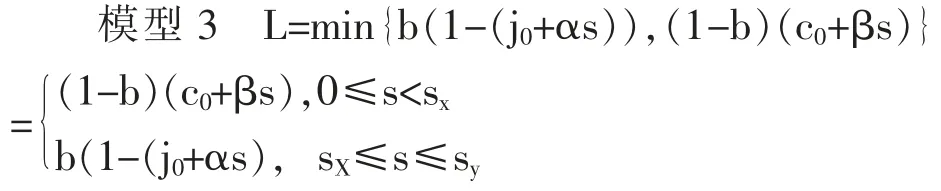
其中，模型3 中的b（1-（j0+αs）为精英阶层的空缺比例；（1-b）（c0+βs）为GC 阶层的比例。另外，模型3 中的Sx、Sy的定义分别作如下表示。

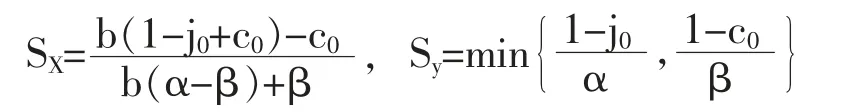
证明：根据词典式次序模型的假设，首先流入到精英阶层的阶层是GJ，即B（GJ）=bj=b（j0+αs），其次能够流入到精英阶层的阶层是GC。因为精英阶层空缺的比例是b-bj，因此形成B（GC）=min{b（1-j0+αs），（1-b）（c0+βs）}的模型。 其中，b（1-j0+αs）为精英阶层的空缺比例，（1-b）（c0+βs）为GC阶层的比例。

根据情境1， 该模型的结果等于社会中的代际上升流动概率（L=B（GC））。另外，模型的结果还可以形成下面四个子模型。通过计算四个子模型，便可以验证模型4 的成立。

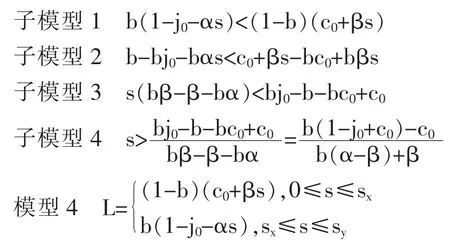
但是，若sx＜0，则往往L=b（1-j0-αs）。 根据命题2，即可明确下面的情境2 所示的问题。

情境2：教育水平和上升流动的关系

教育水平随着时间的推移而提升时，至（α＞0、β＞0），0≤s＜sx以前，代际上升流动概率将会增加，但是在sc≤s＜sx 的范围内， 代际上升流动概率将会降低。此时的代际上升流动概率在s=b（1-j0+c0）-c0/b（α-β）+β 时间点，将达到最大值。 最大值的代际上升流动概率为b（1-b）（c0α+β-j0β/b（α-β）+β。

证明：基于命题2，可以发现：代际上升流动概率L 在0≤s＜sx 的范围内，s 将会增加， 而在sx≤s＜sy的范围内，s 将会减少。 因此，当（1-b）（c0+βs）和b（1-（j0+αs））一致时，L 将变为最大值。据此可以表示为下面的模型5。 另外，若将模型5 的理论值替代代际上升流动概率，则可决定最大值。

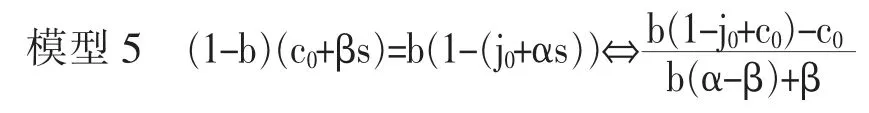
值得注意的是，只要情境2 中，精英阶层的比率b 不发生变化， 则无论怎样的数值均成立。 另外，只要精英阶层的比例保持固定不变，则代际上升流动概率会随着教育水平的提升而在较短时间内会变得降低。

在现实社会， 草根阶层的教育水平往往会低于精英阶层。另外，目前我国，随着年代的推移，草根阶层和精英阶层的教育水平均呈提升之势。 虽然教育水平的提升可见于每一个职业阶层， 但是就高等教育而言， 教育水平还是明显地存在着阶层间的差异。教育水平保持着阶层间的差异，在该条件下，有关代际流动，模型将会预测怎样的问题呢？ 根据命题2 和情境2，即可明确以下情境3 所示的问题。

情境3： 教育水平差异的固定与上升流动的减少。

当精英阶层和草根阶层的教育水平保持着固定差异提升时， 代际上升流动概率在短时间内将会变得下降。

证明：教育水平的差异以固定态势增大，在数学层面，与α=β＞0 的条件相同。此种场合下，根据命题2 和情境2， 明确了代际上升流动概率在以下模型6 的时间点将会提升，而过了这个时间点，则会降低。 也就是说，若教育水平在维持着阶层间差异的状态下不断提升，则代际流动概率必然下降。

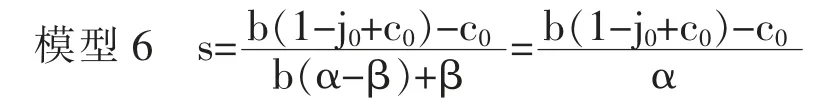
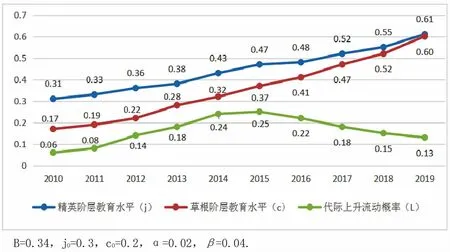
图3 2010-2019年代际上升流动概率L 的变化

在现实社会， 精英阶层出身者和草根阶层出身者的大学教育水平正在维持着阶层间差异共同提升。 那么，教育水平的差异不存在时，将会产生怎样的问题呢？仅凭直觉即可发现：若精英阶层和草根阶层的教育水平变得一致， 以教育水平为中介， 则草根阶层流入到精英阶层的代际流动将会增加，因此上升流动率将会提升。 但是，布登通过数值计算的实例表示：即使教育机会均等化，代际上升流动的概率也会降低（Boudon，1973）。 下面，就用我们的模型证明一下可以一般化的数值实例成立的条件。在同样的假设下，由词典式次序模型推导出的代际上升流动概率的变化，如图3 所示。

可以发现， 因为导入参数后的数值j0＞c0、α＜β， 因此虽然最初草根阶层的教育水平c 很低，但提升途径很多，在短短的九年间（2010-2019年）就接近精英阶层的教育水平j。 图2 中，时间（s）在2019年附近，精英阶层和草根阶层的教育水平变得基本一致，阶层间的教育水平差异仅为0.01，几乎接近于零。 但是， 代际上升流动的概率L 在2015年的时间点由上升转为下降。 也就是说，精英阶层和草根阶层的教育水平变得均等化以前，流动的开放性变得弱化。 图3 仅仅表示了一个特殊的计算例子，还需要提供其成立的一般性条件。

命题3：教育机会均等化以前的封闭性条件

在b＜（j0β-c0α）/（β-α）的条件下，精英阶层与草根阶层的教育水平共同提升， 一直到变得一致时，代际上升流动概率的峰值一定会在此以前出现。

证明：精英阶层和草根阶层的教育水平一致时，j=c⇔s=c0-j0/α-β 的公式成立，即当时间点s=（c0-j0）/（α-β）时，精英阶层和草根阶层的教育水平变得一致。 根据命题2，明确了代际上升流动的概率L处于s=sx时间点时，将会达到峰值。这两个时间点的差，如下面的模型7 所示。

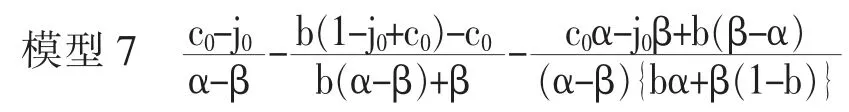
若该模型7 的值为正数， 则教育机会均等化之前， 代际上升流动的概率L 就会降低； 若为负数，则教育机会均等化之后，L 就会降低。 分母处于j0＞c0、α＜β 的条件下，即在“本来最初很低的草根阶层的教育水平， 不久达到甚至超过精英阶层的教育水平”的条件下，通常为负数。 有关b，分子也变为负数的公式是：c0α-j0β+b（β-α）＜0⇔b＜j0βc0α/β-α。 该条件下，在教育机会变得均等化之前，代际上升流动的概率L 一定会下降。

命题3 是运用布登的模拟方法不能够计算出的一般性命题。教育水平的上升和代际流动封闭性的关系能够通过高学历代替的方式进行部分说明。但是， 教育机会的均等化与固定化的时机的关系，该命题虽说简单，但却是一个只能运用数理模型才能推导出的非自明性的复杂命题。 另外，下面有关量化关系的命题不能够从虚拟的说明中导出。

命题4：精英阶层比例b 越高，代际上升流动概率达到峰值的时间点则越迟缓。另外，精英阶层的初期教育水平j0和草根阶层的初期教育水平c0越高， 则代际上升流动概率达到峰值的时间点越提前。

证明： 将代际上升流动概率达到最大值的时间点设定为k（s），则可以从下面的模型8 中得到验证。

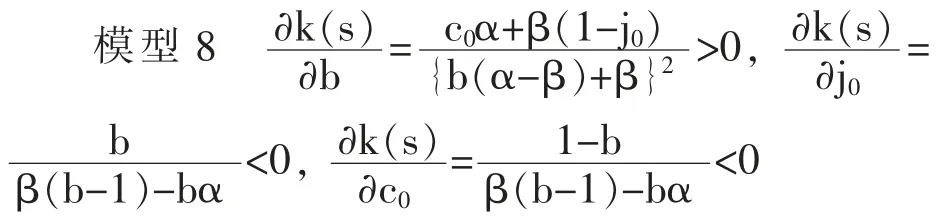
命题5： 代际上升流动概率的最大值是精英阶层的初期教育水平j0的减少函数， 另外还是草根阶层的初期教育水平c0的增加函数。

证明： 将代际上升流动率的最大值设定为r，则可从下面的模型9 中获得验证。

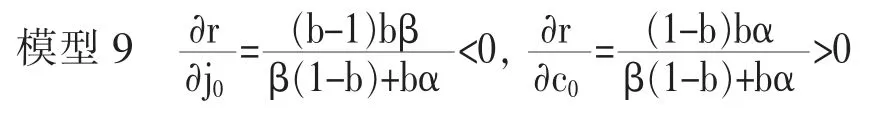
以上所述是根据词典式次序模型推导出的有关教育水平与代际上升流动关系的主要理论命题。

三、教育至上模型

词典式次序模型中， 运用了作为选拔基准产生作用的因素，首先是教育水平，其次是出身阶层的假设。 为此，明确了一个悖论现象，即随着教育水平的普遍提升， 代际上升流动概率L 下降。 另外，通过不同模型的分析，其产生的条件与时机也在数学层面得以明确。

但是，在现实社会，代际流动的过程中，也会有以下两种情境：（1）在教育水平之后，出身阶层作为选拔基准完全不产生作用；（2）即使产生作用，但作用非常小。 布登发现：与英国和法国相比，在美国，父辈职业对于本人职业的影响非常小，而本人的教育水平对于到达阶层的影响却非常大。 另外，为了模拟分析美国社会的这一现象，布登提出了新的假设：仅有教育水平可以作为选拔的基准，而出身阶层等教育水平以外的基准可以被忽略（Boudon，1973：66-67）。以下，基于该假设，以教育至上模型公式化的形式， 分析其与词典式次序模型的不同。该分析中，教育至上模型和词典式次序模型共同拥有假设1 和假设2， 假设3 做如下修改，另外新增了假设4。 其他基本概念的定义与词典式次序模型相同。

（一）教育至上模型的假设

（1）职业与经济地位分为精英阶层（J）和草根阶层（C）。整个社会的精英阶层和草根阶层的比例分别设定为b和1-b。 在代际间，该比例固定不变。

（2）精英阶层和草根阶层的教育水平分别设定为j 和c。 教育水平设定为高（G）和低（D）两个层次。

（3）无论出身阶层如何，均为教育水平高者首先流入到精英阶层。

（4） 教育水平高者流入到精英阶层的机会比例用系数w（0＜w≤1）表示。

有关新增的假设4 做如下说明。 流入机会的比例w 取0，1 之间的数值。 比如0.8，该数值意味着教育水平高者中， 有80%的机会可以流入到精英阶层。 如果阶层的空缺数量少于教育水平高者数量时，则在空缺中，80%的机会提供给教育水平高者。因此，前面分析的词典式次序模型可以看做w=1 的特殊情况。 w=1 表示的是，流入到精英阶层的机会来临时，抓住该机会的概率为1。 其他的基本设计与前面的第二部分（词典式次序模型的基本假设）相同。 本部分分析的概率因时而变，即假设为j=j0+αs，c=c0+βs，α、β＞0。

命题1：教育至上模型的代际上升流动概率L的模型，如下面的模型1 所示。

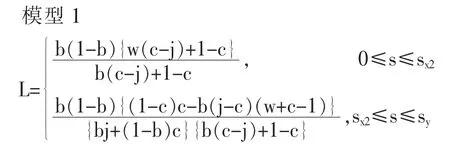
证明： 教育水平高者的比例低于精英阶层比例的条件，如模型2 所示。

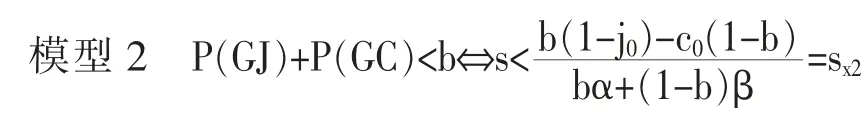
在模型2 的范围（0≤s＜sx2）内，符合B（GJ）=wbj，B（GC）=w（1-b）c 条件者，可以流入到精英阶层。 将也因w 值的高低而决定精英阶层空缺的比例设定为g（w）=b-{B（JG）+B（JD）}=b-{wbj+w（1-b）c}。 此种情境下，教育水平低者流入到精英阶层的比例，可分别用模型3 和模型4 表示。

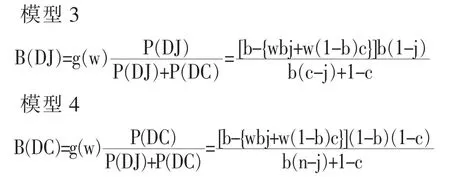
上述模型3 和模型4 中的P（DJ）和P（DC）的值，如前面的计算式（1）中所述。一方面，当教育水平高者的比例变得高于精英阶层的比例时 （sx2≤s≤sy时），教育水平高者流入到精英阶层的比例，如下面的模型5、模型6 所示。

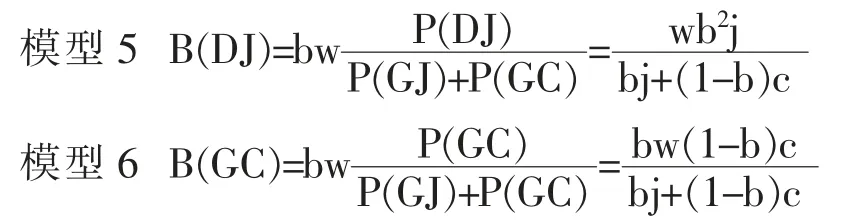
若0＜w≤1，教育水平低者也仅剩b-{B（GJ）+B（GC）}=b-bw 的空缺位置，因此只有符合以下模型7 和模型8 条件者，才能够流入到精英阶层。以上所述，验证了命题1 的成立。

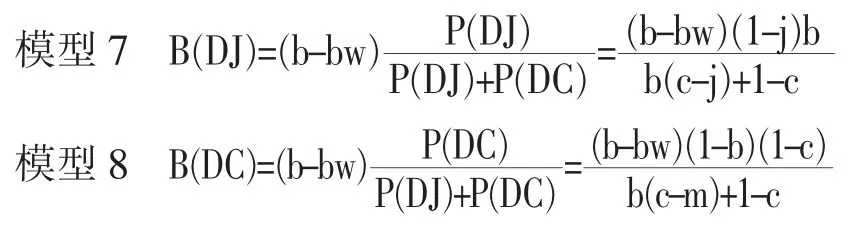
本文关注的问题是： 即使在仅仅重视教育的教育至上社会，伴随着教育水平的提升，代际流动的封闭性也会变得增强， 该悖论现象是否能够产生？ 在w=1 的情境下，下面的命题7 将会成立。

命题2：w=1 的情境下， 在教育至上社会，若j0＞c0、α＞0、β＞0， 则代际上升流动的概率L 在s 方面会出现上升或者下降的倾向。因此，随着教育水平的提升，L 不会产生在起始阶段上升，而随后又转变为下降的悖论现象。

证明：w=1 的情境下，代际上升流动概率L 的模型，可用模型9 表示

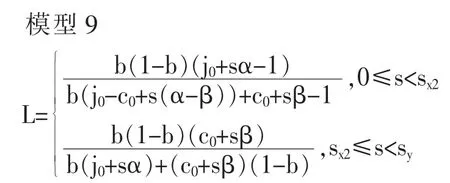
若用时间s 将代际上升流动概率L 用偏微分方程表示，则在0≤s＜sc2的范围内，即可形成模型10。

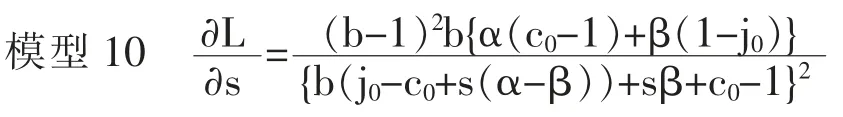
无论怎样的情境下，分母均为正数，因此分子也为正数。 换句话说，若α（c0-1）+β（1-j0）＞0⇔1-j0/1-c0＞α/β，则变为∂B/∂s，反之，若（1-j0）/（1-c0）＜α/β，则为∂B/∂s＜0。 另一方面，在sx2≤s＜sy的范围内，则形成下面的模型11。

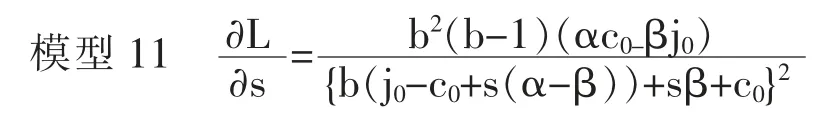
因此，当（n0/m0）＜（β/α）时，则变为∂S/∂t＞0。 此情况下，在的范围内，（1-m0）/（1-n0）＞α/β 成立。 此时，在的范围内，则∂B/∂s＞0。因为m0＞n0，因此可形成下面的模型12。

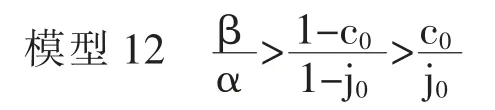
因此，即使在sx2≤s＜sy的范围内，仍然会∂B/∂s＞0，此情境下，代际上升流动概率L 在s 方面将会呈上升之势。 反之，在（1-j0）/（1-c0）＞α/β 的情境下，将会呈降低之势。 因此，代际上升流动概率L在开始期间 （时间点在的范围内， 变得∂B/∂s＞0时）上升，随即又变得降低（时间点在sx2≤s＜sy的范围内，变得∂B/∂s＜0 时）。 该现象意味着（1-j0）/（1-c0）＞α/β，且（c0/j0）＜（β/α）相互矛盾的状况存在，因此在现实中，一般不会出现。

当w=1.2 时， 则说明该社会为视教育水平为唯一选拔基准的教育至上社会，此情境下，在现实中的参数范围内不会产生与之相反的悖论。 当w＜1.2 时，结果将具有很强的复杂性，因此基于命题6 形成的代际上升流动概率L 的计算事例，如图4所示。

为了具有可比性， 使用了与计算图3 时相同的参数。 从图4 中可见，当w=1.2 时，代际流动概率L 并非随时间而降低，但当w=0.6 时，时间点在2014年达到峰值后， 随即又变得逐渐降低。 图4中， 虽然没有显示精英阶层和草根阶层的教育水平，但可以发现：精英阶层和草根阶层的教育水平均随着时间的推移呈现提升之势（α、β＞0），教育水平的阶层间差异也逐渐变得缩小（β＞α）。 图4的计算结果说明三个问题：（1）与出身阶层无关的教育至上主义；（2）教育水平正在提升；（3）阶层间教育水平的差异正在缩小。 这三者进而说明了一个很违背现实的事实存在， 即虽然具备了非常有利于代际上升流动的条件， 但代际上升流动率有时也会降低。

要确定产生这种悖论式的代际上升流动率降低的一般性条件， 实现代际上升流动比例w≠1，该过程却非常复杂。 虽然没有像词典式次序模型那样获得简单的结果， 但还是尽量将条件做如下限定。根据定义，因为L=B（GC）+B（DC），因此可以进行分解，分析各项的变化。首先，有关B（GC），可以成立以下的命题8。

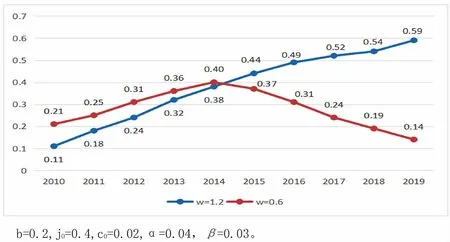
图4 教育至上社会中，代际上升流动概率L 的变化

命题3：当B（GC）为β＞0 并且c0/j0＜β/α 时，0≤s＜x2将会增加。 在的范围内，若β＜0，则s 将会减少。

证明：根据前面的命题1 的证明，将j=j0+αt、c=c0+βt 导入到B（GC），将会形成下面的模型13。

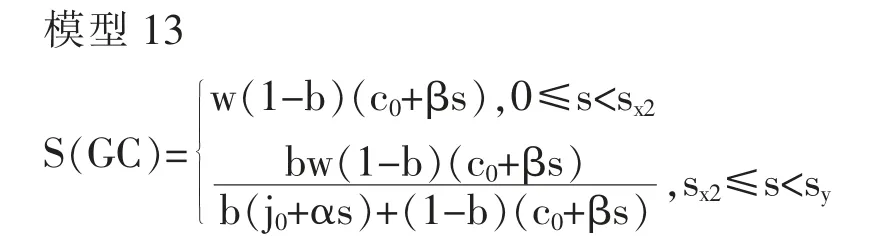
当0≤s＜sx2时，则∂B（GC）/∂s=w（1-b）β。 右边的w，（1-b）一定为正数，因此若β＞0，则变为∂B（GC）/∂s＞0。 反之，若β＜0，则变为∂B（GC）/∂s＜0。另外，当sx2≤s＜sy时，则形成下面的模型14。

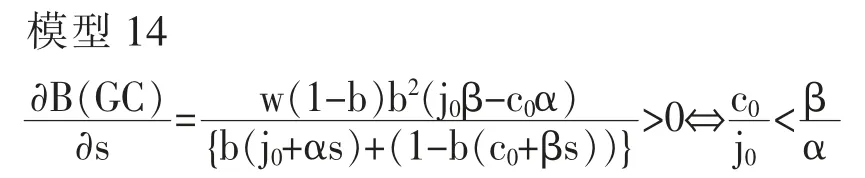
因此，满足该条件时，模型14 中的B（GC）在s 方面呈增加之势。那么，模型14 中的c0/j0＜β/α 条件下的经验意义是什么呢？ 在包括中国在内的很多社会， 初期精英阶层和草根阶层的教育水平的关系呈现c0/j0，因此c0/j0＜1。 阶层研究已有的发现说明：α=β 的现象经常产生，因此可以说：c0/j0＜β/α是现实社会很容易成立的条件。也就是说，在经验层面，B（GC）在s 方面增加的可能性很大，因此若代际上升流动概率L 随着时间的推移呈下降之势，则可以推测：那主要是因B（DC）的减少而引起。 现在，若将j=j0+αs、c=c0+βs 导入到B（DC），则会产生下面的模型15。

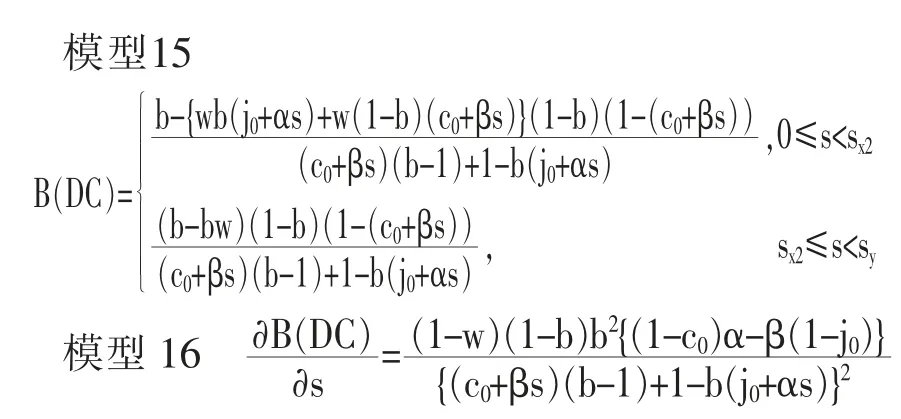
在sx2≤s＜sy的范围内， 由于可形成上面的模型16， 因此在下面模型17 的条件下， 在时间方面，B（DC）将会减少。

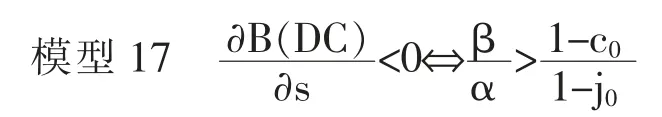
若从精英阶层、 草根阶层的初期教育水平的经验层面的数值考虑， 因为1-c0＞1-j0， 因此模型17 的右侧公式的结果有很大的可能性会变得大于1。 因此，在sx2≤s＜sy的范围内，若使得B（DC）减少，α＜β 是必要条件。另外，词典式次序模型中，在sx2＜s＜sy的范围内，w=1 的情境下， 将会变得B（DC）=0， 因此很难出现DC 阶层上升流动的机会（见情境1）。 而教育至上模型与词典式次序模型不同，若w＜1，则B（DC）≠0，因此即使DC 阶层也会有上升流动的机会。 在现实生活中，经常可以发现DC 阶层流入到精英阶层的事例， 因此可以说，就与数据契合性的意义而言，教育至上模型与词典式次序模型相比，具有更强的解释力。 需要说明的是，在0≤s＜sx2的条件下，模型的计算相当复杂，偏导函数的经验解释也非常困难，因此本文略去该部分的分析，而作为今后的课题进行研究。

四、数据的匹配与今后的研究课题

在该部分， 将确认根据词典式次序模型和教育至上模型推导出的代际上升流动概率的理论值、 优势比的理论值， 分别与中国综合社会调查（Chinese General Social Survey，CGSS）2010 至2019年的调查数据计算出的经验值的匹配度。 与前面的分析相同， 该部分的分析仍然将专业技术职业和管理职业的阶层视作精英阶层， 将大学本科及以上的学历视作高等教育水平。 为了推导出理论值，将模型均处理为无时间模型。各个年度的精英阶层教育水平j 和草根阶层教育水平c 运用经验值， 精英阶层的比例b 是运用本人为专业技术职业和管理职业的比例，而不是父辈职业。 表1表示的是，2010-2019年间随着年代的推移，有关代际上升流动的理论值与经验值的关系变化倾向，可以发现以下三种变化倾向。

（1）经验值随着年代的推移呈现递增之势，2010年为0.312，而2019年已增加至0.962。

（2） 由词典式次序模型推导出的上升流动概率的理论值，因为假设B（DC）=0，因此数值普遍变得很低。最低值为2010年的0.102，最高值也仅为2014年的2.232。

（3）无论任何年代，词典式次序模型推导出的上升流动概率的理论值均显著地低于教育至上模型的理论值。比如：词典式次序模型的理论值和教育至上模型的理论值，2010年分别为0.102 和0.224，后者高于前者一倍之多；而2019年分别变化为0.108 和0.628，后者高于前者五倍之多。

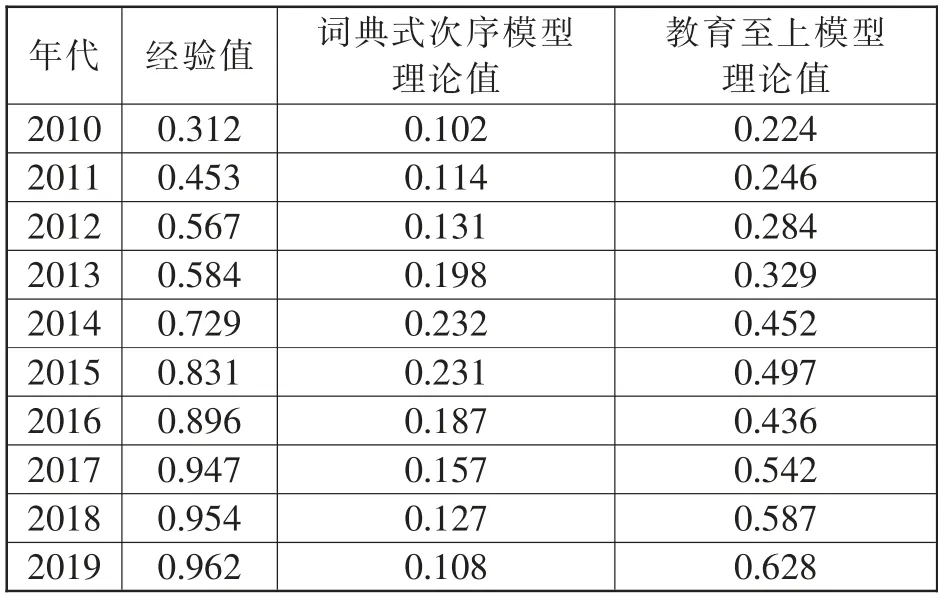
表1 代际上升流动概率的推移：理论值与经验值的关系

表2 表示的是，2010-2019年间随着年代的推移精英阶层优势比的经验值和理论值的变化情况，可以发现以下三种变化情况。

（1） 经验值的最大值为2015年的0.431，最小值为2010年的0.206。另外，2010-2015年间随着年代的推移呈现增加之势，而其后则呈现减少之势；

（2）词典式次序模型的理论值的最大值为2010年的0.612， 最小值为2014年的0.412。 另外，2010-2014年间随着年代的推移， 理论值呈现减少之势，而2015-2019年间随着年代的推移，理论值却呈现增加之势。

（3）教育至上模型的理论值的最大值为2016年的0.597， 最小值为2010年的0.420。 另外，2010-2016年间随着年代的推移， 理论值呈现增加之势，而2017-2019年间随着年代的推移，理论值却呈现减少之势。

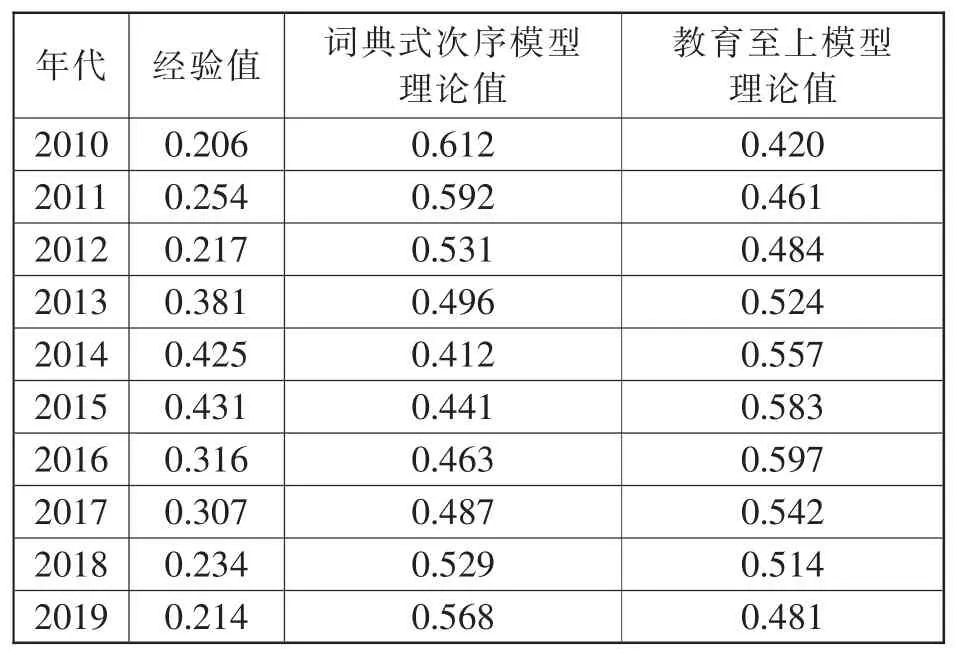
表2 精英阶层优势比的推移：理论值与经验值的关系

表1 和表2 的数据说明： 从经验数值匹配的角度看，教育至上模型的适用性很好，而词典式次序模型在优势比方面存在很大的偏差。 这意味着若出身阶层的影响适用于布登的图式， 则在现阶段，中国社会比英国和法国，更与美国接近一致，已经变化为出身阶层的影响相对小的社会。

在本文，作为理论分析，有关公式化的教育水平与代际流动的模型， 不仅推导出了一个非常复杂的理论命题，而且保持与经验数据的匹配性，从该意义上说，本文的分析较为准确、透彻。但是，本文的模型运用宏观层面的变量说明宏观层面的现象， 没有将说明微观层面的个人行为的理论（模型）联系起来。作为说明是否获得大学本科及以上教育水平这一个人层面的行动的主要理论， 学术界已经提出了人力资本理论（Becker，1993）、相对风 险 规 避 理 论 （Breen and Goldthorpe，1997；Goldthorpe，2000）、 学历下降规避理论 （吉川，2006）等。但是，如何运用数学方法，将这些有关阶层流动的微观机制编入到本文的模型， 进而推导出更为全面、准确的数理模型，是留作今后的一个研究课题。