执行器故障下的运载火箭非奇异终端滑模容错控制

马艳如，王 青，胡昌华，周志杰，梁小辉

(1. 北京航空航天大学自动化科学与电气工程学院，北京 100191；2. 火箭军工程大学导弹工程学院，西安 710025)

0 引 言

近年来，随着航空航天技术的发展，运载火箭成为人类进入太空的重要工具，承担任务种类愈加复杂，承载载荷愈发多样[1]。例如，中国的长征系列运载火箭和美国NASA的Ares系列运载火箭、美国太空探索技术公司(SpaceX)猎鹰系列运载火箭等[2]，承担发射不同地球轨道卫星和载人飞船的任务。发射任务一旦失败，不仅会带来巨大的经济损失，还会影响其战略、军事、外交等[3]。然而，运载火箭发射失败的主要原因是控制精度不够和机械故障等。因此，在如此耗资巨大和复杂的系统中，提高系统的控制精度和在故障下仍能保持良好的控制性能显得尤为重要。滑模控制因其对外界干扰和不确定参数具有强鲁棒性、快速全局收敛特性和对建模误差不敏感等特性。广泛应用于机器人控制、化工控制和航空航天等领域[4-6]。传统滑模控制采用线性滑模面，不具备有限时间收敛特性[7]，而非奇异终端滑模控制不但能实现有限时间收敛，而且改进了传统的终端滑模控制存在控制输入趋于无穷大的问题，成为当前研究热点，并取得了一定成果。

非奇异终端滑模控制方法在航天器控制方面取得了许多成果[8-12]。文献[8-12]考虑模型不确定性和外部干扰的情况对控制器进行设计；不同之处在于文献[8]构造了固定时间扩张状态观测器，用于估计外部干扰和不确定状态的总扰动，设计了一种新的非奇异快速终端滑模面，并根据总扰动的估计和提出的滑模面设计了相应的固定时间控制器。文献[9]重点解决具有未知边界扰动的挠性航天器有限时间姿态控制问题。文献[10]针对航天器姿态跟踪控制问题提出一种复合控制器。该控制器由非奇异终端滑模法的反馈控制和基于有限时间扰动观测器的补偿项组成。文献[11]设计了非奇异快速终端滑模动态输出反馈控制器，仅利用角速度和角度信息实现有限时间快速姿态稳定。文献[12]在反步法中最后一步设计了终端滑模控制法，以保证有限时间收敛。众多文献[13-15]对更为复杂的模型控制问题作了研究。文献[13]针对存在模型不确定性的再入飞行器提出了基于神经网络的固定时间终端滑模控制律，引入饱和函数以避免奇异性问题。自适应神经网络用于估计飞行器的不确定性，从而在不牺牲鲁棒性的情况下减轻了颤动。文献[14]基于非奇异终端滑模技术和径向基神经网络设计了航天器编队飞行多目标姿态跟踪鲁棒控制器。鲁棒控制器由径向基神经网络和自适应控制器组成，并根据非奇异终端滑模有限时间收敛特性，提出了一种径向基网络在线学习算法，提高其逼近效率。文献[15]将非奇异终端滑模控制与自适应方法相结合，自适应更新律用于估计各种不确定性的边界。

与上述方法不同，本文提出了一种新型非奇异终端滑模控制设计方法，将应用于单输入单输出(SISO)系统的终端滑模方法[16]扩展到多输入多输出(MIMO)非线性系统，且考虑系统在执行器卡死故障下的控制。首先，本文针对存在执行器卡死故障的运载火箭姿态跟踪系统设计了一种新型终端滑模面，基于李雅普诺夫函数证明系统能在有限时间到达滑模面。而对于奇异问题，本文修改了奇异区域的控制律。当闭环系统到达滑模面后，原点是该系统的全局渐近稳定点。能较快实现运载火箭姿态跟踪系统的控制。

本文对存在执行器卡死故障的运载火箭姿态控制跟踪问题进行研究。首先对运载火箭姿态控制系统进行动力学建模；在此基础上考虑未知干扰和执行器故障建立系统模型，执行器故障主要考虑执行机构卡死故障，将干扰和执行器故障视为广义干扰，并将系统转换为一种多输入多输出系统，该系统为三个独立的二阶单输入单输出微分方程。利用非奇异终端滑模控制技术，实现了故障下的运载火箭姿态角非线性跟踪控制，同时保证运载火箭的控制精度。

1 系统动力学模型

图1 运载火箭发动机布局尾视图

(1)

(2a)

(2b)

对于某大型运载火箭，忽略弹性模态，并将燃油晃动和气动力矩考虑到干扰中，建立其旋转运动模型：

(3)

式中：J=diag(Jxx,Jyy,Jzz)∈R3×3为运载火箭的转动惯量矩阵；ω=[ωx,ωy,ωz]T为角速度；矩阵κ定义为：

(4)

式中:u为控制输入向量；ufault为执行器故障输入矩阵；D=[Dx,Dy,Dz]T为干扰向量。

式(3)中的控制输入力矩u由6个发动机摆动产生。其中，控制力矩为：

(5)

式中:R=3 m和r=1 m分别为助推发动机中心和芯级发动机中心到运载火箭箭体x轴的距离。XR为发动机喷嘴到火箭顶端的距离；XZ为质心位置；P为每个发动机的推力。将式(1)代入式(5)，可得：

u=Bδ

(6)

式中:B为输入矩阵，其中

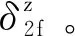
(7)

C=Pdiag(-4R,-2(XR-XZ),-2(XR-XZ))。

根据惯性坐标系与机体坐标系之间的关系，可以得到运载火箭姿态运动方程为：

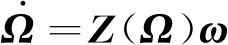
(8)

式中:Ω=[φ,φ,θ]T，φ为滚转角，φ为偏航角，θ为俯仰角。其中，Z(Ω)的定义为：

(9)

根据式(1)～(9)，建立运载火箭动力学模型：

(10)

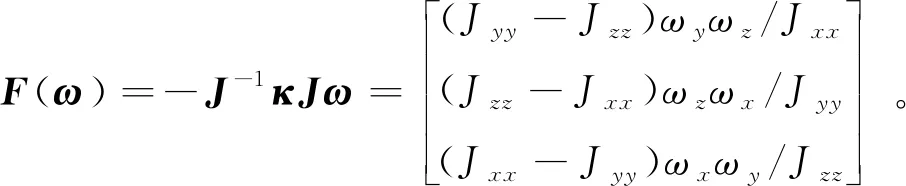
式(10)中的第一项对时间微分，可得：

(11)

由式(10)可得：

(12)

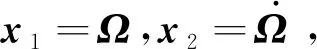
(13)

式中:f(x)∈R3，G(x)∈R3×3，d∈R3。其中，上述三项的定义为：

(14)

令xr为运载火箭姿态角参考信号，即xr=[φr,φr,θr]T，φr,φr,θr分别为滚转角、偏航角和俯仰角参考信号。定义系统误差信号：

(15)

为简化闭环跟踪控制系统问题，给出下述假设条件。

假设1[17]. 在任意t>0时刻，令λ=(ufault+D)，并定义λ′=[|λ1|, |λ2|, |λ3|]T，且广义干扰λ′均有上届λup，其中λup∈R3，定义λ′≤λup,即|λi|<λiup,i=1,2,3。

假设2[16]. 控制输入向量δ(t)∈L2空间，即δ(t)在任何有限时间内的积分均有界。

假设3[17]. 姿态角指令参考信号xr和其前二阶导数均可得到且有界。

本文的控制目标为设计控制器δ(t)使得满足上述假设条件的运载火箭姿态系统(10)能在有限时间跟踪到期望值，并且有良好的控制精度，即：

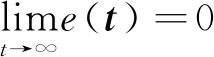
(16)

2 非奇异终端滑模控制器设计

(17)

对于式(17)所描述的系统，本文设计了一种非奇异终端滑模控制器，实现对火箭姿态角的快速跟踪。首先介绍本文在设计控制器时所用到的引理。

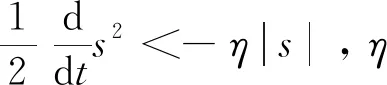
设计如下终端滑模面：

s=v2+c1v1+c2sigβ(v1)

(18)

式中：s=[s1,s2,s3]T∈R3,0<β<1。其中定义c1v1=c1[v11,v12,v13]T,且c1,c2满足c1,c2>0，sigβ(v1)=[sigβ(v11), sigβ(v12), sigβ(v13)]T,定义sigβ(x)=|x|βsgn(x)，其中，符号函数sgn(x)定义为：

并令：

h′(v1)=c1v1+c2sigβ(v1)

(19)

由式(19)可知：limz→0h′(z)=0。

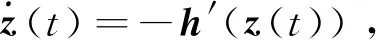
(20)

由式(20)可知，V1>0,并对V1求导可得：

-zT(t)(c1z(t)+c2sigβ(z(t)))=

-c1zT(t)z(t)-c2zT(t)sigβ(z(t))=

(21)

定理1. 对于运载火箭姿态控制系统(10)，如果假设1～3都成立，根据式(18)所设计的终端滑模控制律保证该系统在有限时间内跟踪参考信号，控制律如下：

δ=δeq+δd

(22)

(23)

证. 首先选取如下李雅普诺夫候选函数：

(24)

(25)

将式(22)和(23)代入式(25)可得：

(26)

将式(26)代入可得：

(27)

由引理1，系统可在有限时间到达滑模面s=0，假设到达滑模面时间为Tr。由式(18)可得：

(28)

由此可知，可以利用定理1所提出的控制律实现运载火箭姿态跟踪系统有限时间收敛。

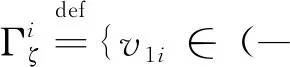
(29)

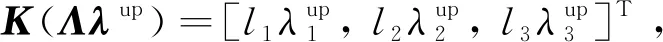
综上所述，下面给出非奇异终端控制律：

(30)

3 仿真校验

本文以文献[17]中运载火箭姿态控制系统为例，校验所提出的非奇异终端滑模控制方案的有效性。运载火箭总飞行时间为160 s，每个发动机的推力为P=1200000 N，转动惯量(Jxx,Jyy,Jzz)和火箭在质心位置Xz是时间的线性函数，表1给出了具体参数。初始姿态角为x1(0)=[-0.1, 10.1, 79.9]T。姿态控制系统的参考信号xir，i=1,2,3分别为：

式中:ω1,2=0.1,ω3=0.05,ζ1,2,3=1,p1,3=0.2,p2=0.4。本文设置助推发动机2在初始时刻卡死，且卡死角度为5°，之后助推发动机2摆角保持常数不变。图2～4为运载火箭故障下姿态角跟踪轨迹。其中，图2为滚转角跟踪轨迹；图3为偏航角跟踪轨迹；图4为俯仰角跟踪轨迹。由图2～4可知，通过设计的非奇异终端滑模控制律，可以保证姿态角能够跟踪控制指令。图5为姿态角跟踪误差，姿态角初始值存在一定的误差，随着时间变化，误差逐渐减小，并在稳态时误差角小于0.02°，由此可知运载火箭姿态角控制精度较好。此外，由图5可知，偏航角和俯仰角误差角度为0时，其导数不为0，即本文的奇异区域，本文通过修改该区域的控制律避免奇异问题的出现。且与文献[17]对比，本文设置的故障角度较大，但最终误差角相比更小，具有更高的控制精度。图6为整角速度ω=[ωx,ωy,ωz]T的变化曲线。图7为助推发动机摆角变化曲线，由图7可知，初始时刻助推发动机2卡死，摆角保持在5°不变，系统稳定之后，助推发动机1、3、4的摆角不为0，保持在某个常数。图8为芯级发动机摆角变化曲线，由图可知，当系统稳定后，芯级发动机的摆角同样保持在某个不为0的常数。即当某个发动机发生故障如卡死故障时，本文所设计的控制律借助其余助推发动机和芯级发动机来平衡该故障带来的影响。由图2～4可知，运载火箭发动机发生故障后，姿态角仍能较好跟踪参考信号。因此，本文提出的基于非奇异终端滑模控制策略可以控制故障下运载火箭姿态跟踪系统，且具有良好的控制精度。

表1 运载火箭仿真中的参数Table 1 Parameter of launch vehicle used in numerical simulations

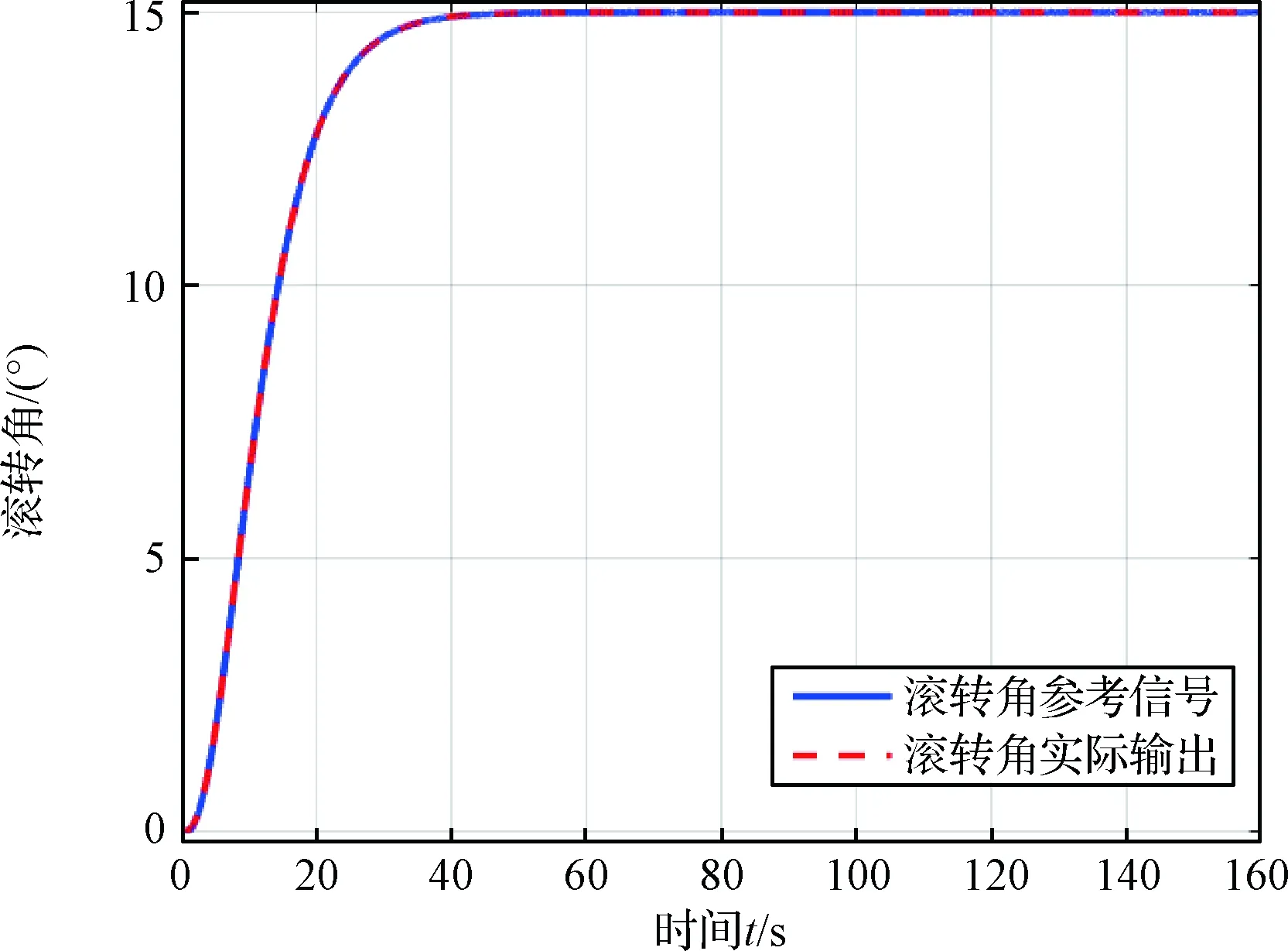
图2 滚转角跟踪轨迹

图3 偏航角跟踪轨迹

图4 俯仰角跟踪轨迹

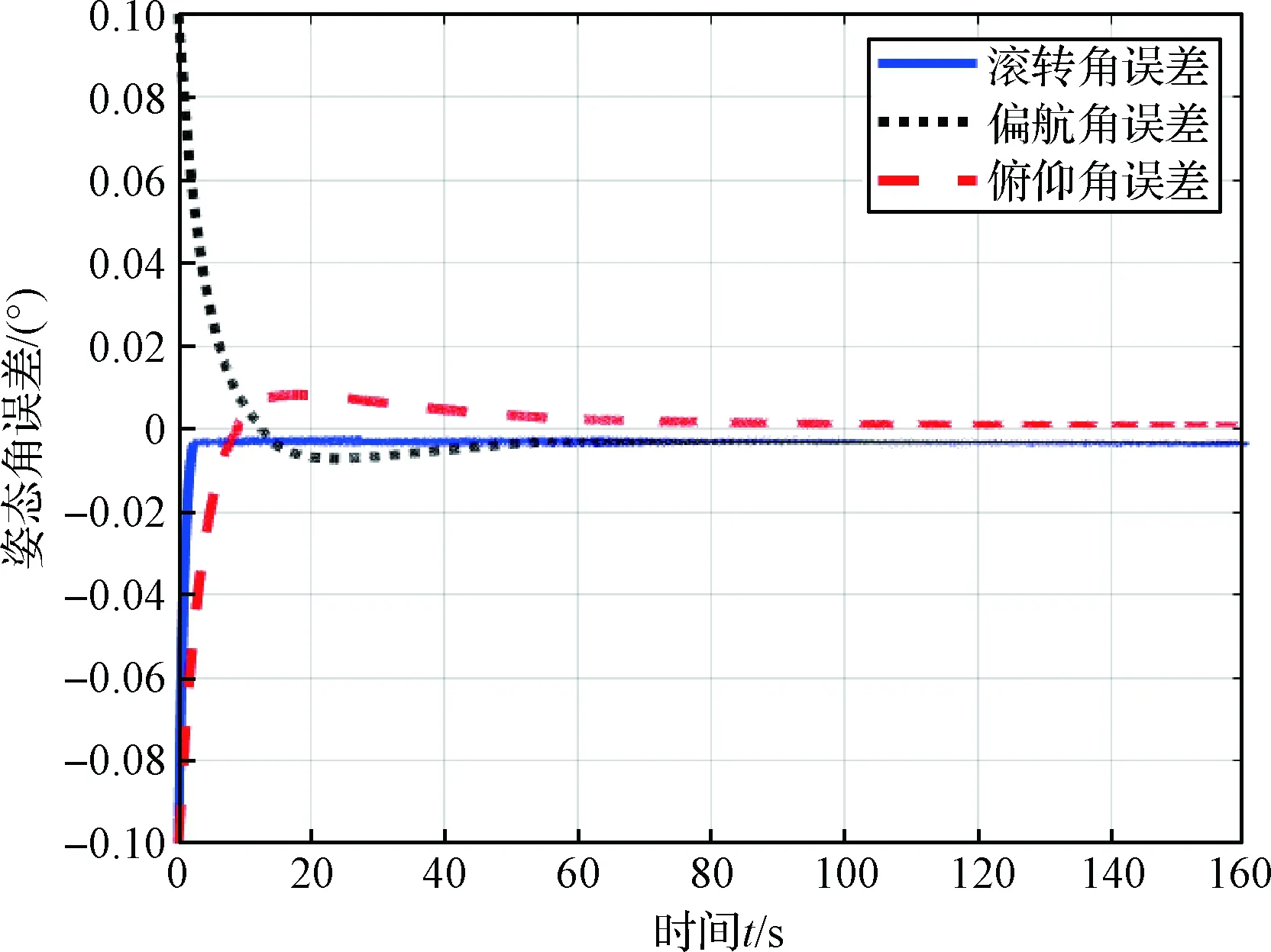
图5 姿态角跟踪误差

图6 角速度变化曲线

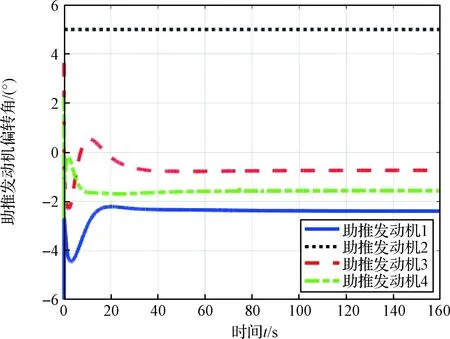
图7 助推发动机偏转角度曲线

图8 芯级发动机偏转角度曲线

4 结 论

本文研究了考虑外部干扰和执行器卡死故障的运载火箭姿态跟踪控制问题，将执行器卡死故障视为广义干扰，在此基础上设计了基于李雅普诺夫函数的非奇异终端滑模控制律。所设计的控制律使得系统闭环轨迹快速到达滑模面并在滑模面上收敛到零。本文通过修改奇异区域的控制律，避免出现奇异问题。所设计的控制律实现了故障情况下对运载火箭姿态角精确跟踪的控制目标，通过仿真可以进一步校验所得到的结论。